Признаки возрастания и убывания функции
Если для функции f (х) в каждой точке промежутка Х производная функции f ' (х) > 0, то на данном промежутке Х функция возрастает, f ' (х) < 0, то на данном промежутке Х функция убывает.
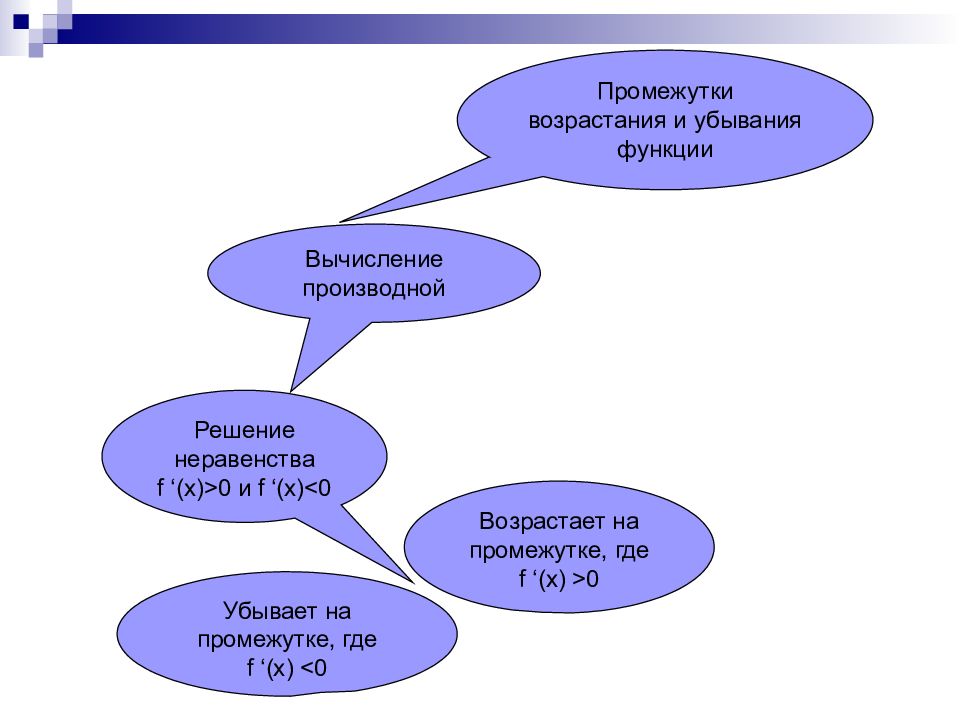
1. найти область определения функции 2.вычислить производную функции 3.решить неравенство f ‘(x) > 0 или f ‘(x) < 0 4. Используя утверждение теоремы, найти промежутки возрастания и убывания функции Алгоритм нахождения промежутков возрастания и убывания функции
Домашнее задание №261 а) у=15-2х-х 2 у ‘ =-2 -2х -2-2х > 0 -2 -2х < 0 -2х > 2 -2х < 2 х > -1 х < -1 возрастает убывает (-1, +∞) (-∞, -1)
Домашнее задание №261 б) у=1/3х 3 -1/2х 2 у ‘ = х 2 -х х 2 -х > 0 х(х-1) > 0 +. -. + 0 1 (-∞,0) и (1, +∞) возрастает (0, 1) убывает
у = 7х²+12х -5 у = 6 cos 2х +4х у= 3х² – 8х³ у = 6х² + 2 cos х – 12 у = 7х + 4х³ -21 + х4
№ 263 б) f (х)=2х 3 -3х 2 -12х-1 f ‘ (х)=6х 2 -6х-12 х 2 -х-2=0 Д=1+8=9 х 1 =2, х 2 =-1 + -1 - 2 + (- ∞,-1) и (2,+∞)возрастает (-1, 2) убывает
№ 262 б) у=х/(х+2) у ‘ = х ‘ (х+2) – х(х+2) ' = х+2-х (х+2) 2 (х+2) 2 (х+2) 2 > 0, значит у '> 0 функция возрастает
Найди производные функций у=6 Sin х+5 у=3х 2 +5х-1 у=х 3 -2х 2 +2х у = Cos (2х+4) -1 у= 6х 2 +4х-5 у= (2х+1) 3 у= 5 Sin 2х + 8 Выполни задание
у ‘ = 3х 2 -4х+2 г у ‘ = 12х+4 а у ‘ = 6 Cos х л у ‘ = 6(2х+1) 2 н у ‘ = 6х+5 а у ‘ = 10 Cos х ж у ‘ = -2 Sin (2х+4) р Получи слово
Понятие производной возникло в 17 в. в связи необходимостью решения задач по физике, механике и математике, в первую очередь следующих двух: определение скорости движения и построение касательной к произвольной плоской кривой. Математиков 15-17 вв. долго волновал вопрос о нахождении общего метода для построения касательной в любой точке. Некоторые частные случаи решения задач были даны еще в древности. Так, в «Началах» Евклида дан способ построения касательной к окружности, Архимед построил касательную к спирали, Аполлоний – к эллипсу, гиперболе и параболе. Историческая справка
С самого начала 17 в. немало ученых, в том числе Торричелли, Вивиани, Барроу, пытались найти решение вопроса, прибегая к кинематическим соображениям. Первый общий способ построения касательной к кривой был изложен в «Геометрии» Декарта. Более общим и важным для развития дифференциального исчисления был метод построения касательных Ферма. Основываясь на результатах Ферма и некоторых других выводах, Лейбниц гораздо полнее своих предшественников решил задачу, о которой идет речь, создав общий алгоритм. Обозначения у ‘ и f ‘ (х) для производной ввел Лагранж. Историческая справка
1) Функция у=3х 2 +6х возрастает на промежутке (-1, + ∞) 2) Функция у=1/3х 3 -9х убывает на промежутке (-∞, 3) 3) Функция у=5х 2 +7 убывает на промежутке (-∞, 0) 4) Функция у=3х 2 -12х+1 возрастает на промежутке ( -∞, 2) Графический диктант
Да Нет График
Промежутки возрастания и убывания функции Вычисление производной Решение неравенства f ‘ (х) >0 и f ‘(x)<0 Возрастает на промежутке, где f ‘(x) >0 Убывает на промежутке, где f ‘ (х) < 0
