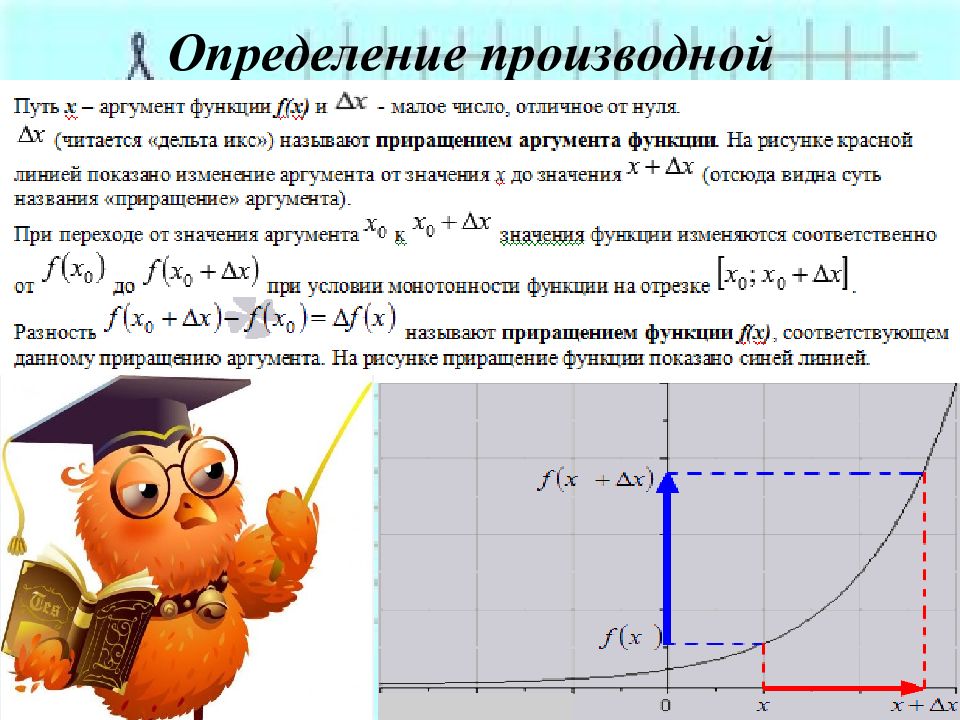
Первый слайд презентации
Презентация на тему «Производная и правила ее вычисления»
Слайд 6: Решение задач
Найти производную функции Пример №1 Общая формула производной степенной функции: Производная от x равна 1, следовательно 7*1 и получаем просто 7
Слайд 7: Пример №2
Найти производную функции Общая формула производной степенной функции: Общая формула дифференцирования произведения:
Слайд 8: Пример №3
Найти производную функции Общая формула производной степенной функции: Общая формула дифференцирования частного:
Слайд 9: Пример № 4
Найти производную функции Cos (5x – 3) Находим для начала производную от функции cos x, она будет равна – sin x. Так как у нас под знаком cos стоит функция следовательно мы должны найти производную от функции f ( 5 x – 3 ). Она будет равна 5 по формуле дифференцирования линейной функции. F ’(5 x – 3) = 5 ( формула f ’( kx – b ) = k ) Следовательно f ’( cos (5 x – 3) = - 5 sin (5 x – 3)
Слайд 10: Пример № 5
Найти производную функции Для начала перепишем корень в виде степени с рациональным показателем: f(x) = (x 2 + 8x − 7) 0,5 Теперь делаем замену: пусть x 2 + 8x − 7 = t. Находим производную по формуле: f ’(x) = f ’(t) · t ’ = (t 0,5 )’ · t ’ = 0,5 · t −0,5 · t ’ Делаем обратную замену: t = x 2 + 8x − 7. Имеем: f ’(x) = 0,5 · (x 2 + 8x − 7) −0,5 · (x 2 + 8x − 7)’ = 0,5 · (2x + 8) · (x 2 + 8x − 7) −0,5 Наконец, возвращаемся к корням: