Общие уравнения прямой Параметрические уравнения прямой Векторное уравнение прямой Канонические уравнения прямой Уравнение прямой, проходящей через две точки Взаимное расположение двух прямых Взаимное расположение прямой и плоскости
l ( 1 ) Система уравнений (1) определяет прямую в пространстве тогда и только тогда, когда коэффициент не пропорциональны коэффициентам. Аксиома линия пересечения двух плоскостей – прямая. Общие уравнения прямой Теорема
Пусть прямая в пространстве, проходит через точку M 0 ( x 0 ; y 0 ; z 0 ) параллельно вектору Параметрические уравнения прямой Любой ненулевой вектор, параллельный прямой в пространстве, называется направляющим вектором этой прямой. Очевидно, что точка М (х; у; z ) лежит на прямой, только в том случае, если векторы и коллинеарны. Тогда по лемме о коллинеарных векторах М 0 (х 0 ; у 0 : z 0 ) М (х; у ;Z) Параметрические уравнения прямой
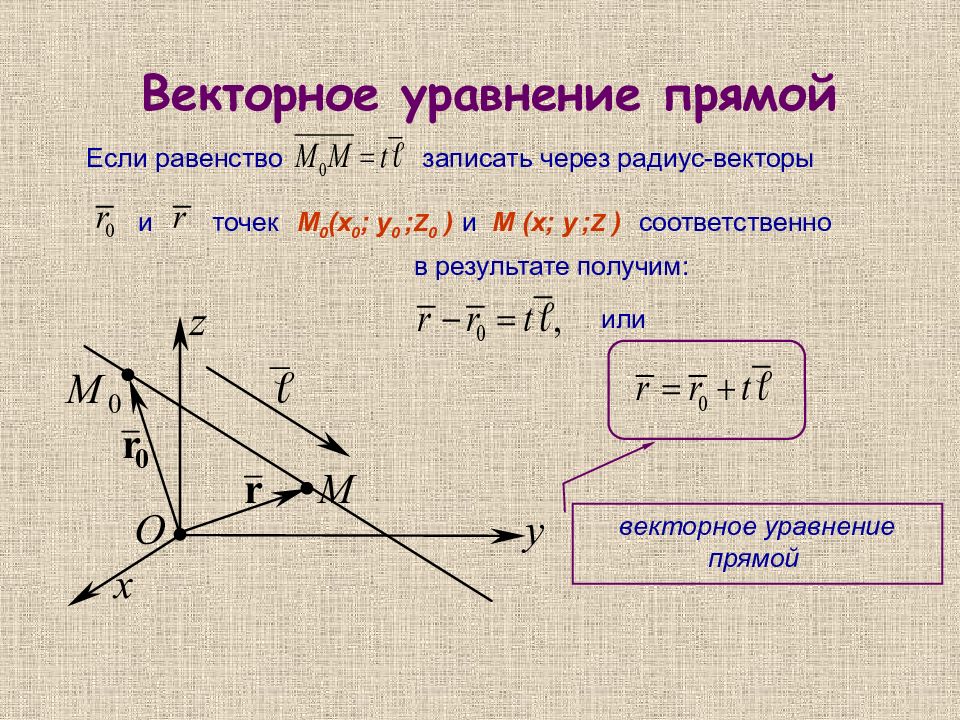
Векторное уравнение прямой Если равенство записать через радиус-векторы и точек и соответственно М 0 (х 0 ; у 0 ; Z 0 ) М (х; у ; Z ) в результате получим: или векторное уравнение прямой
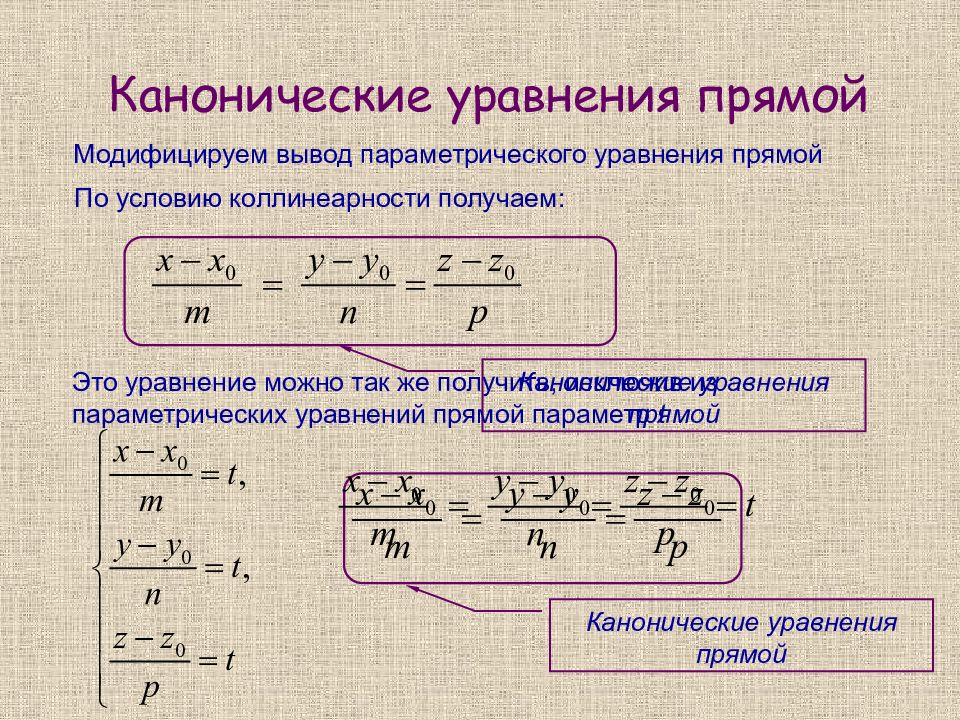
Модифицируем вывод параметрического уравнения прямой По условию коллинеарности получаем: Канонические уравнения прямой Это уравнение можно так же получить, исключив из параметрических уравнений прямой параметр t Канонические уравнения прямой
Пусть прямая проходит через две заданные и отличные друг от друга точки: М 1 (х 1 ; у 1 ;z 1 ) и М 2 (х 2 ; у 2 ;z 2 ). М 1 (х 1 ; у 1 ;z 1 ) М 2 (х 2 ; у 2 ;z 2 ) Тогда в качестве направляющего вектора в каноническом уравнении можно взять вектор: Уравнение прямой, проходящей через две заданные точки Замечание: если в знаменателе одной из дробей стоит нуль, то прямая перпендикулярна соответствующей координатной оси
Пример Написать уравнение прямой, если она проходит через точки с координатами (1; 2; 3) и (3; 2; 1).
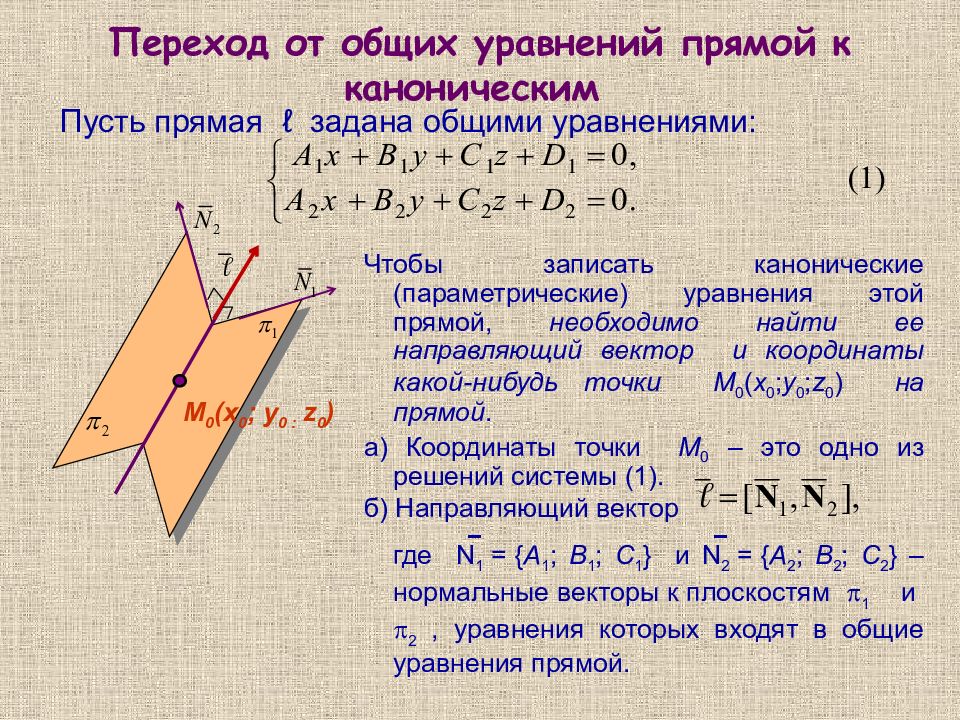
Пусть прямая ℓ задана общими уравнениями: Чтобы записать канонические (параметрические) уравнения этой прямой, необходимо найти ее направляющий вектор и координаты какой-нибудь точки M 0 ( x 0 ; y 0 ; z 0 ) на прямой. а) Координаты точки M 0 – это одно из решений системы ( 1 ). б) Направляющий вектор где N ̄ 1 = { A 1 ; B 1 ; C 1 } и N ̄ 2 = { A 2 ; B 2 ; C 2 } – нормальные векторы к плоскостям 1 и 2, уравнения которых входят в общие уравнения прямой. М 0 (х 0 ; у 0 : z 0 )
Пример Найти координаты точки В, симметричной точке с координатами (2; 3; 1) относительно прямой .
Пример Найти канонические уравнения прямой, совпадающей с линией пересечения плоскостей .
Пример Даны канонические уравнения прямой Необходимо перейти к общим уравнениям .
В пространстве две прямые могут: а) быть параллельны, б) совпадать, в) пересекаться, г) скрещиваться. Пусть прямые ℓ 1 и ℓ 2 заданы каноническими уравнениями 1) Пусть прямые ℓ 1 и ℓ 2 параллельны. Получаем: прямые параллельны их направляющие векторы т.е. выполняется условие: и коллинеарные, и направляющим векторам неколлинеарен М 1 (х 1 ; у 1 ;z 1 ) М 2 (х 2 ; у 2 ;z 2 )
2 ) Пусть прямые ℓ 1 и ℓ 2 совпадают. Получаем: прямые совпадают их направляющие векторы и коллинеарные, т.е. выполняется условие: и направляющим векторам коллинеарен
3 ) Пусть прямые ℓ 1 и ℓ 2 пересекаются. Получили: прямые ℓ 1 и ℓ 2 пересекаются они не параллельны и для них выполняются условия и или, в координатной форме, 4 ) Если для прямых ℓ 1 и ℓ 2 не выполняется условие то прямые скрещиваются.
Возможное расположение прямых в пространстве приводит к следующим задачам: 1) параллельные прямые расстояние между прямыми (т.е. расстояние от точки до прямой)? 2) пересекающиеся прямые а) угол между прямыми? б) точка пересечения прямых? 3) скрещивающиеся прямые а) угол между прямыми? б) расстояние между прямыми? Пусть даны 2 прямые и – направляющий вектор прямой ℓ i, M i ( x i ; y i ; z i ) ℓ i ( i = 1,2).
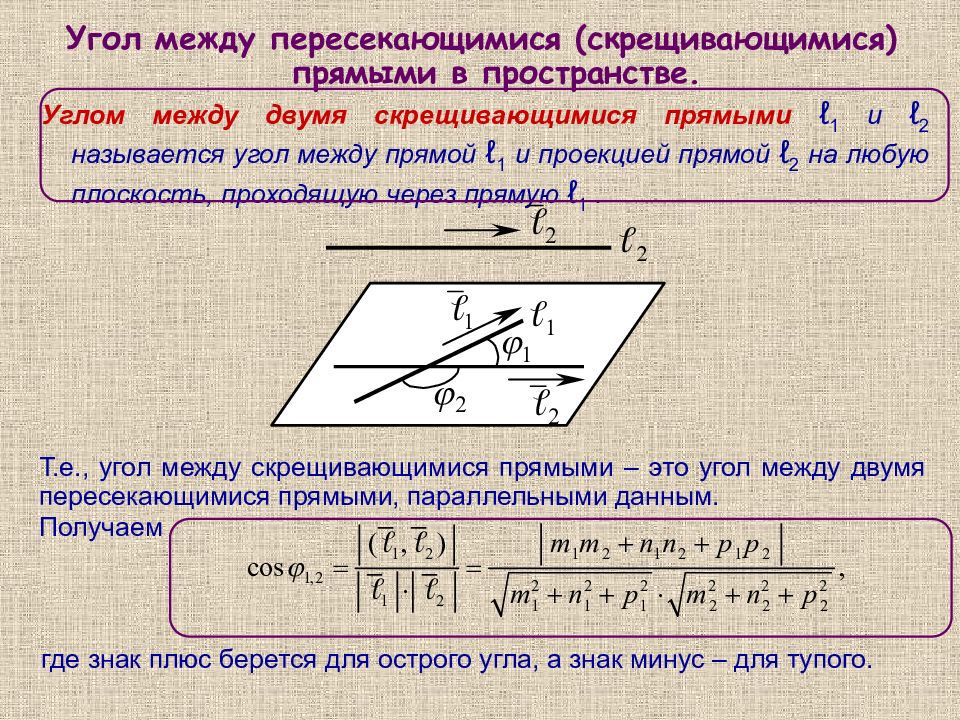
Угол между пересекающимися (скрещивающимися) прямыми в пространстве. Т.е., угол между скрещивающимися прямыми – это угол между двумя пересекающимися прямыми, параллельными данным. Получаем где знак плюс берется для острого угла, а знак минус – для тупого. Углом между двумя скрещивающимися прямыми ℓ 1 и ℓ 2 называется угол между прямой ℓ 1 и проекцией прямой ℓ 2 на любую плоскость, проходящую через прямую ℓ 1.
Пусть дана прямая M 1 ( x 1 ; y 1 ; z 1 ) – точка, не принадлежащая ℓ. – направляющий вектор прямой ℓ, M 0 ( x 0 ; y 0 ; z 0 ) – точка на прямой ℓ, d – расстояние от точки M 1 до ℓ. Расстояние от точки до прямой в пространстве
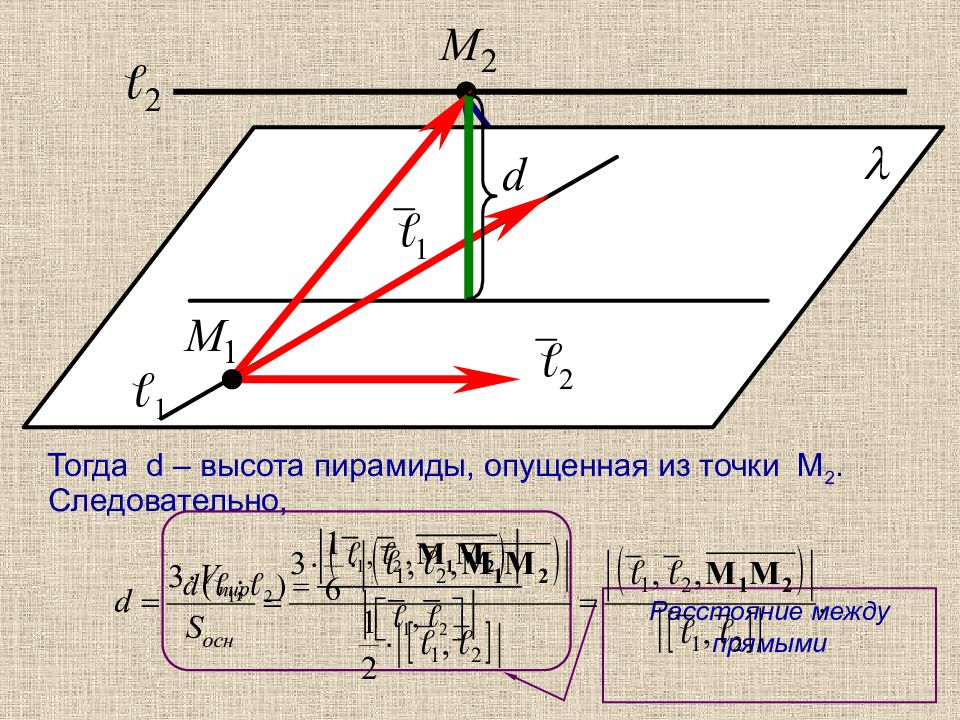
Пусть даны две скрещивающиеся прямые и – направляющий вектор прямой ℓ i, M i ( x i ; y i ; z i ) ℓ i ( i = 1,2). где Ax + By + Cz + D = 0 – общее уравнение плоскости p, M 2 ( x 2 ; y 2 ; z 2 ) – любая точка на прямой ℓ 2. Расстояние между скрещивающимися прямыми Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра.
Тогда d – высота пирамиды, опущенная из точки M 2. Следовательно, Расстояние между прямыми
Пример Исследовать взаимное расположение прямых
Пусть в пространстве заданы плоскость и прямая ℓ. Они могут 1) быть параллельны; 2) прямая может лежать в плоскости; 3) прямая и плоскость могут пересекаться в одной точке. Пусть : Ax + By + C z + D = 0 и Тогда N ̄ = { A ; B ; C } – нормальный вектор плоскости , – направляющий вектор прямой ℓ.
а) Если прямая параллельна плоскости, то или в координатной форме Am + Bn + Cp = 0. ( 1 ) б) Если прямая принадлежит плоскости, то координаты любой ее точки удовлетворяют уравнению плоскости, и, следовательно, кроме условия (1) выполняется условие Ax 0 + By 0 + Cz 0 + D = 0, где M 0 ( x 0 ; y 0 ; z 0 ) – любая точка прямой. в) Если условие (1) не выполняется, то прямая и плоскость пересекаются в одной точке.
Уравнение пучка плоскостей, проходящих через прямую, образованную пересечением плоскостей имеет вид Пучок плоскостей – это множество всех плоскостей в трехмерном пространстве, проходящих через одну данную прямую.
Пример Составить уравнение плоскости проходящей через прямую и параллельно прямой
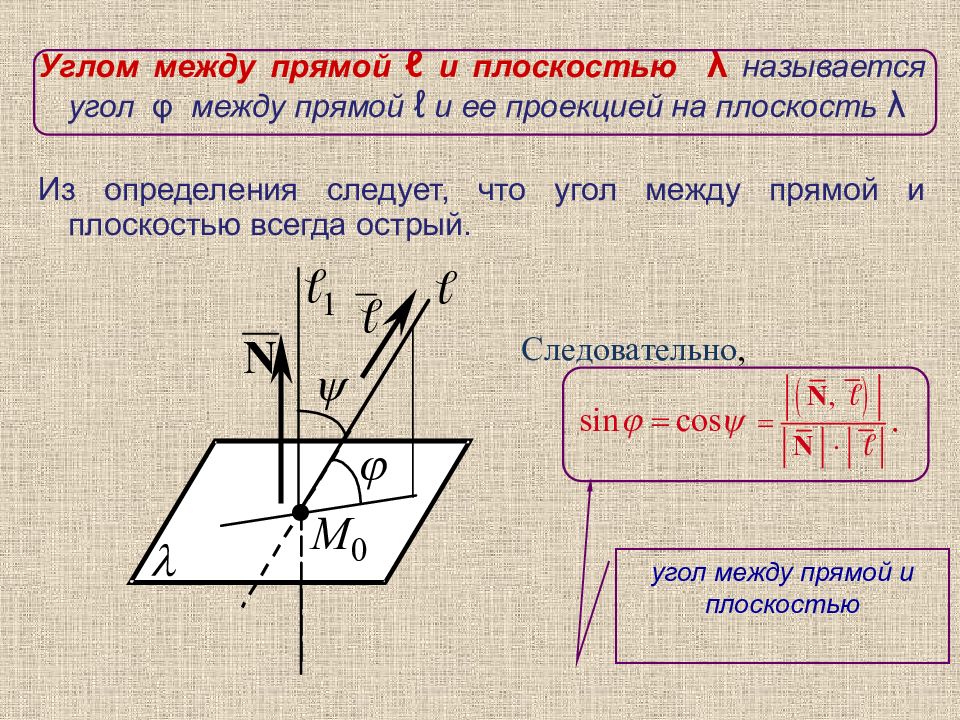
Углом между прямой ℓ и плоскостью λ называется угол φ между прямой ℓ и ее проекцией на плоскость λ Из определения следует, что угол между прямой и плоскостью всегда острый. угол между прямой и плоскостью
Пример Исследовать взаимное расположение прямой и плоскости
