Слайд 2: Вспомни !
Что такое граф? Перечисли его элементы. Где вам встречались графы? Что такое степень вершины графа? Может ли степень вершины равняться 0 ? Сформулируйте теорему о сумме степеней вершин. Вспомни !
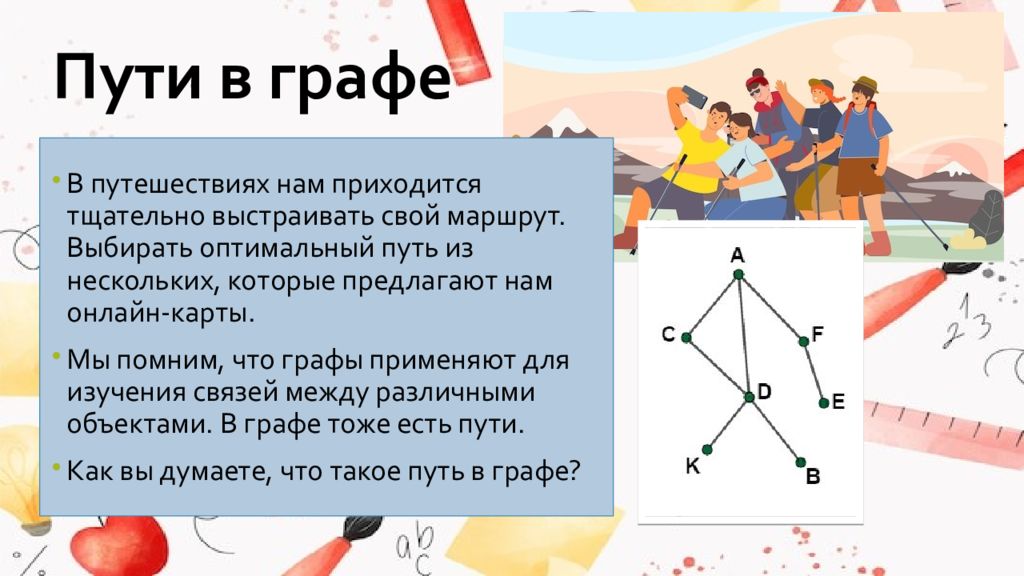
Слайд 3: Пути в графе
В путешествиях нам приходится тщательно выстраивать свой маршрут. Выбирать оптимальный путь из нескольких, которые предлагают нам онлайн-карты. Мы помним, что графы применяют для изучения связей между различными объектами. В графе тоже есть пути. Как вы думаете, что такое путь в графе?
Слайд 4: Запиши!
Путь в графе – это такая последовательность рёбер, в которой каждые два соседних ребра имеют общую вершину.
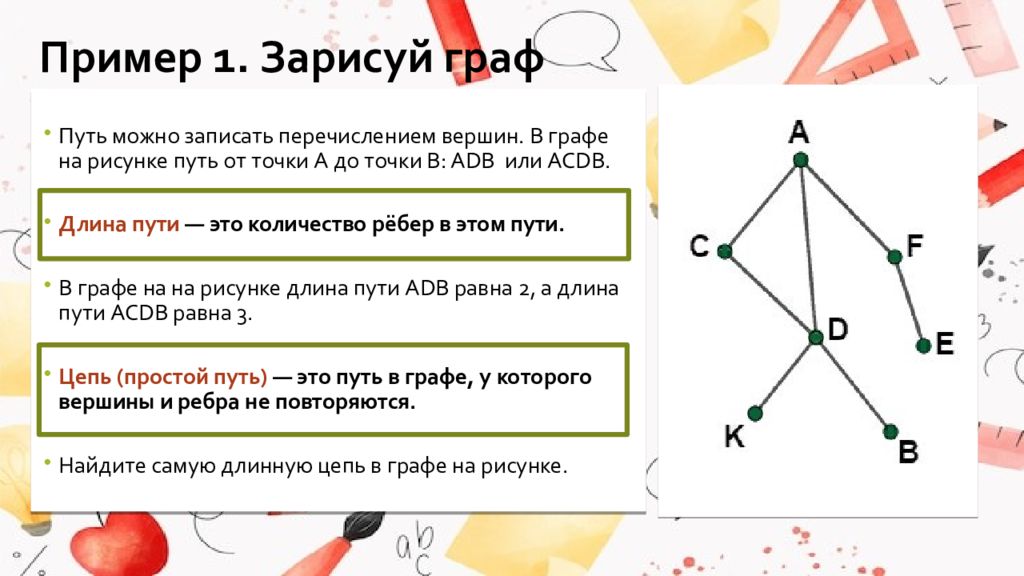
Слайд 5: Пример 1. Зарисуй граф
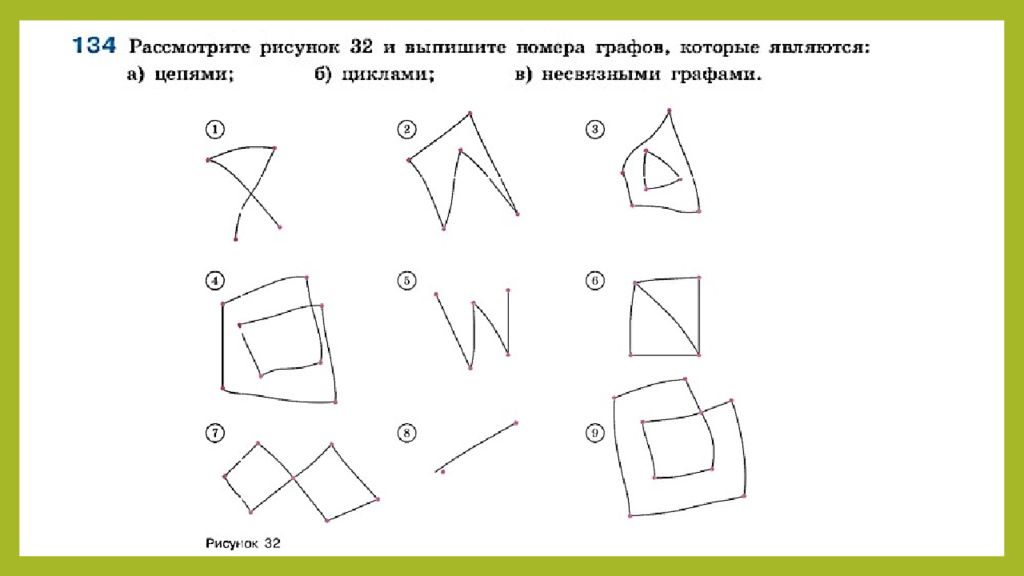
Путь можно записать перечислением вершин. В графе на рисунке путь от точки A до точки B: ADB или ACDB. Длина пути — это количество рёбер в этом пути. В графе на на рисунке длина пути ADB равна 2, а длина пути ACDB равна 3. Цепь (простой путь) — это путь в графе, у которого вершины и ребра не повторяются. Найдите самую длинную цепь в графе на рисунке.
Слайд 6: Цикл в графе
Путешествуя, мы всегда возвращаемся назад. Иногда той же дорогой, иногда другой. Если мы вышли из дома и вернулись другой дорогой, то мы по сути прошли цикл. Цикл в графе — это замкнутый путь, у которого начало и конец в одной вершине, а рёбра и промежуточные вершины не повторяются. Обозначается цикл в примере ACDA, CDAC или АС D. Началом можно считать любую вершину графа. Простейший цикл – петля, состоит из одной вершины и одного ребра.
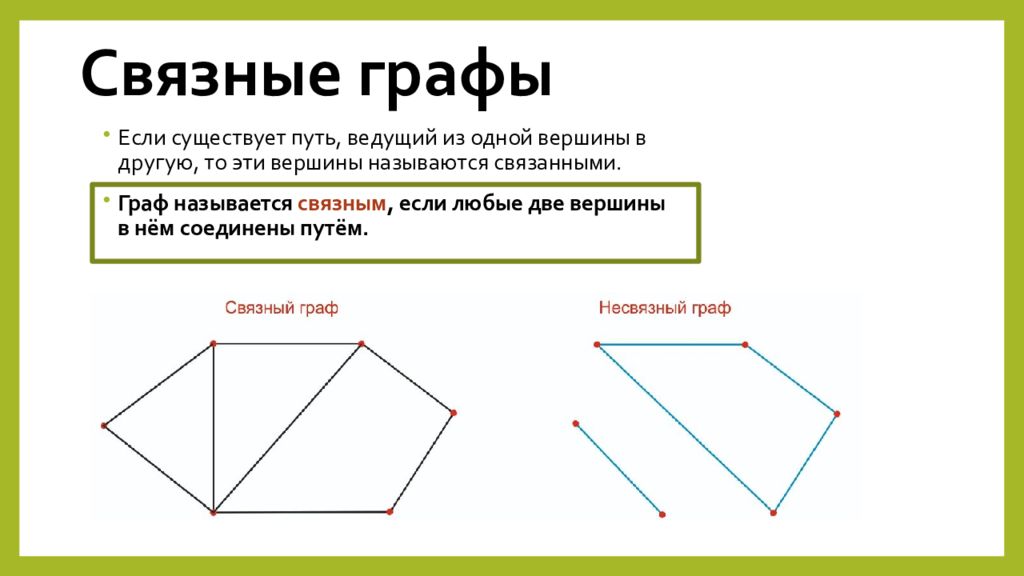
Слайд 7: Связные графы
Если существует путь, ведущий из одной вершины в другую, то эти вершины называются связанными. Граф называется связным, если любые две вершины в нём соединены путём.
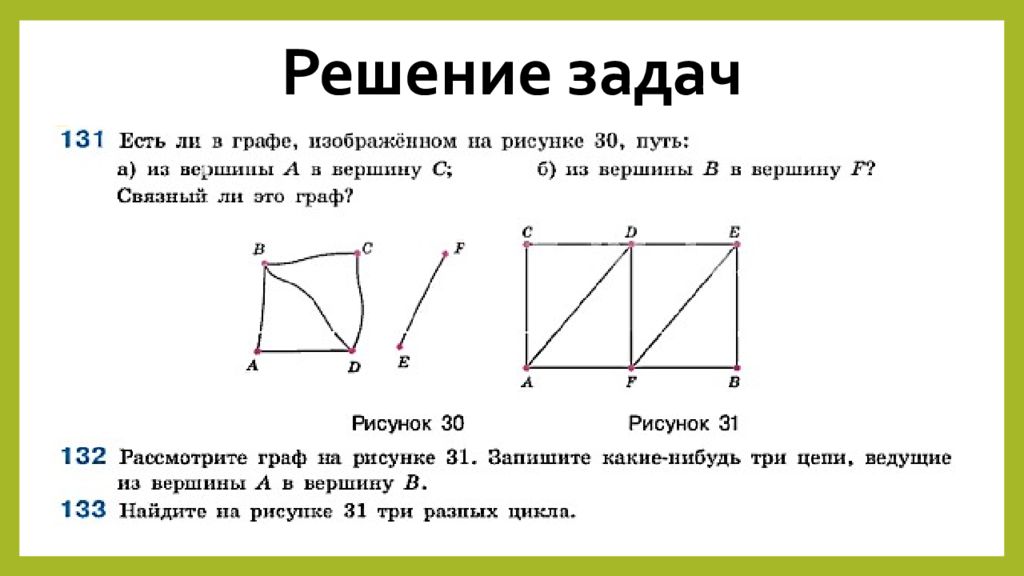
Слайд 10: Подведем итог
Что нового вы узнали о графах сегодня? Поясните, что такое цепь? Что такое цикл? Какой граф называют связным?
Слайд 11: Рефлексия
Отметьте себя на плоскости: понятно – не понятно, интересно – не интересно. Интересно Не понятно Интересно Понятно Не интересно Не понятно Не интересно Понятно не понятно понятно интересно не интересно