Слайд 4: Правило параллелепипеда
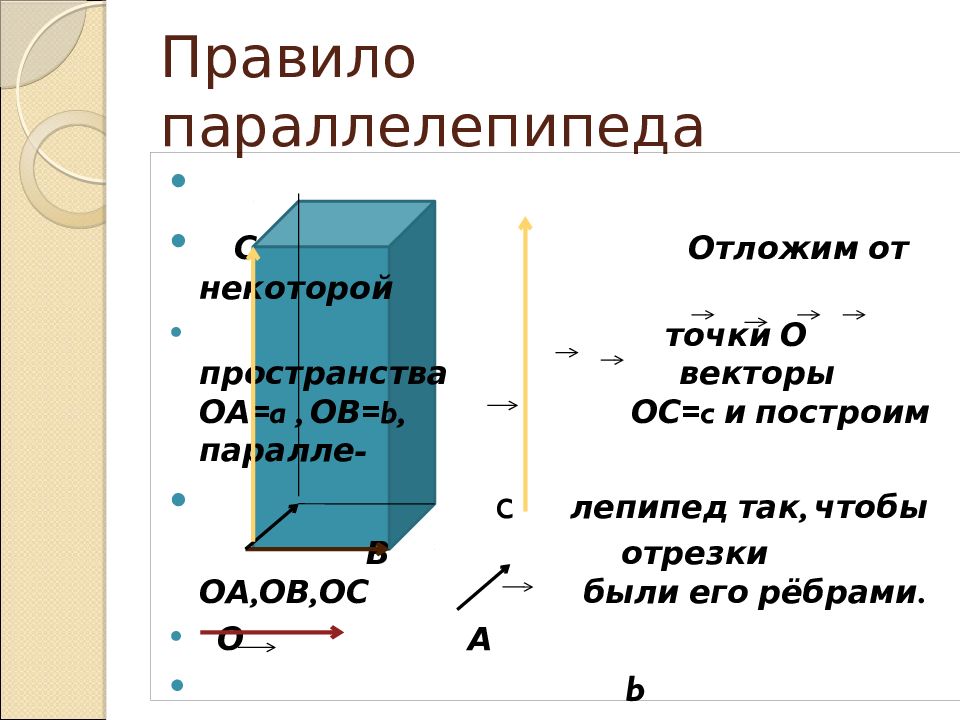
a Пусть даны некоторые некомпланарные векторы c a, b, c b
Слайд 5: Правило параллелепипеда
С Отложим от некоторой точки О пространства векторы ОА= a, ОВ= b, ОС= c и построим паралле- c лепипед так, чтобы В отрезки ОА,ОВ,ОС были его рёбрами. О А b a
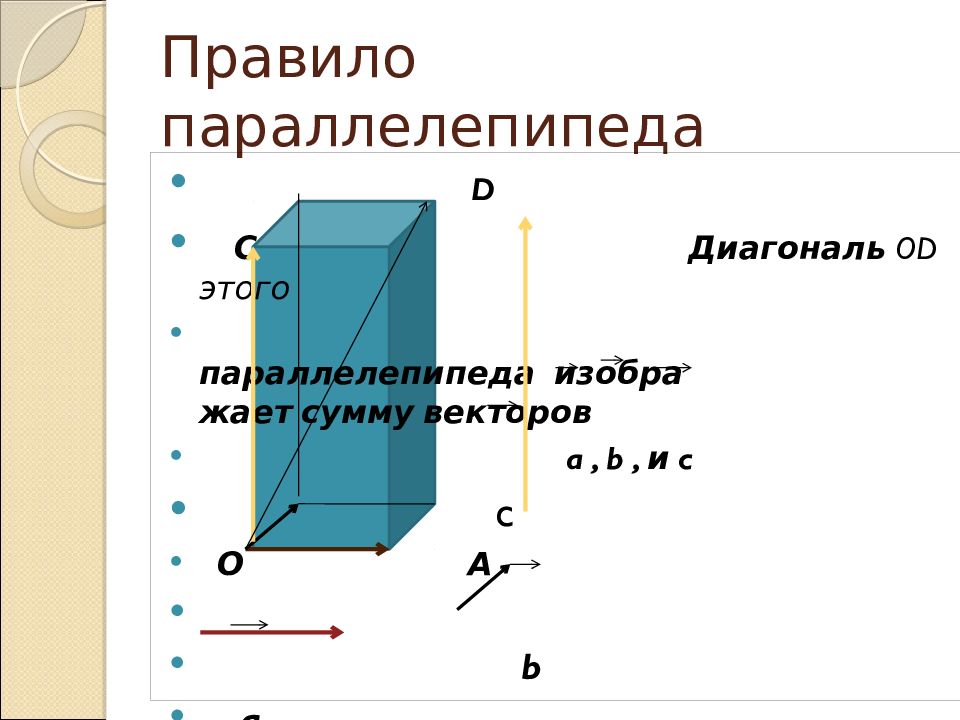
Слайд 6: Правило параллелепипеда
D С Диагональ OD этого параллелепипеда изобра жает сумму векторов a, b, и c c О А b a
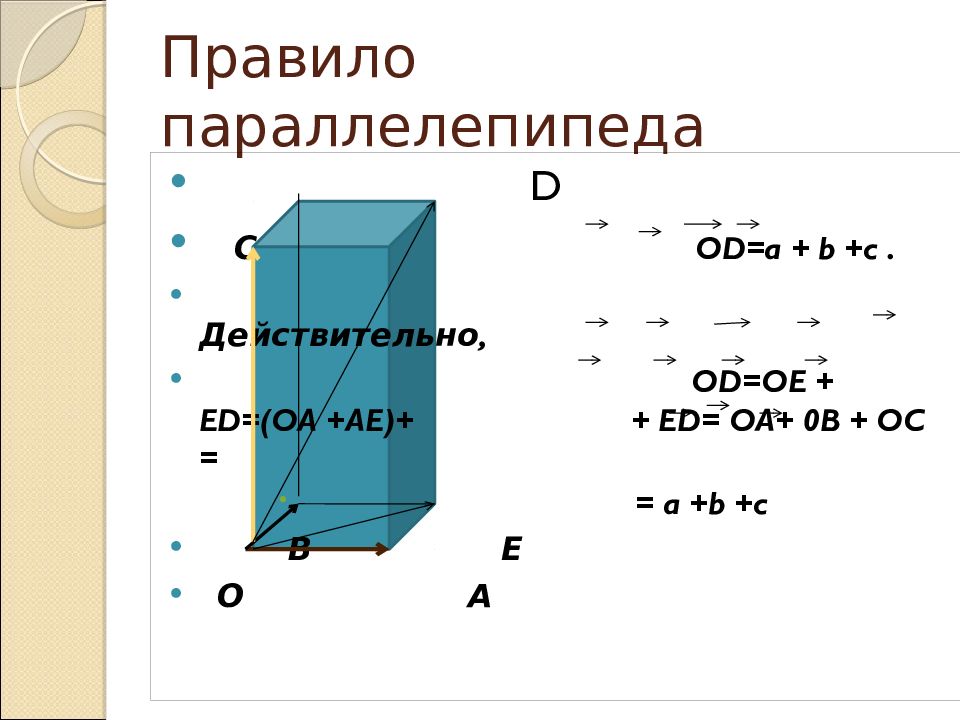
Слайд 7: Правило параллелепипеда
D С OD=a + b +c. Действительно, OD=OE + ED=(OA +AE)+ + ED= OA+ 0B + OC = = a +b +c В Е О А
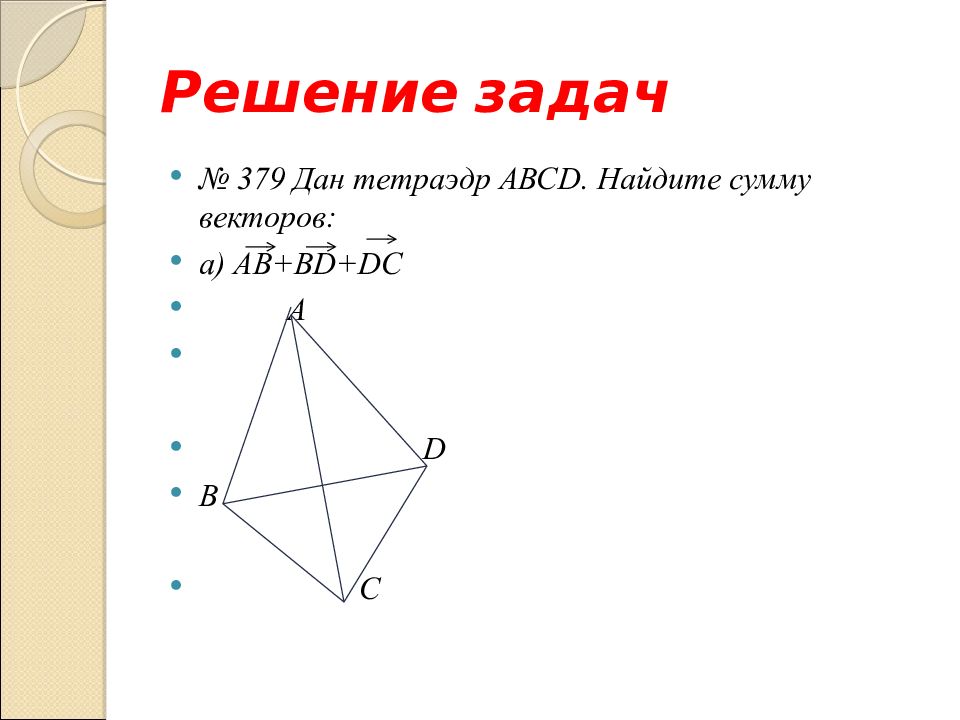
Слайд 8: Решение задач
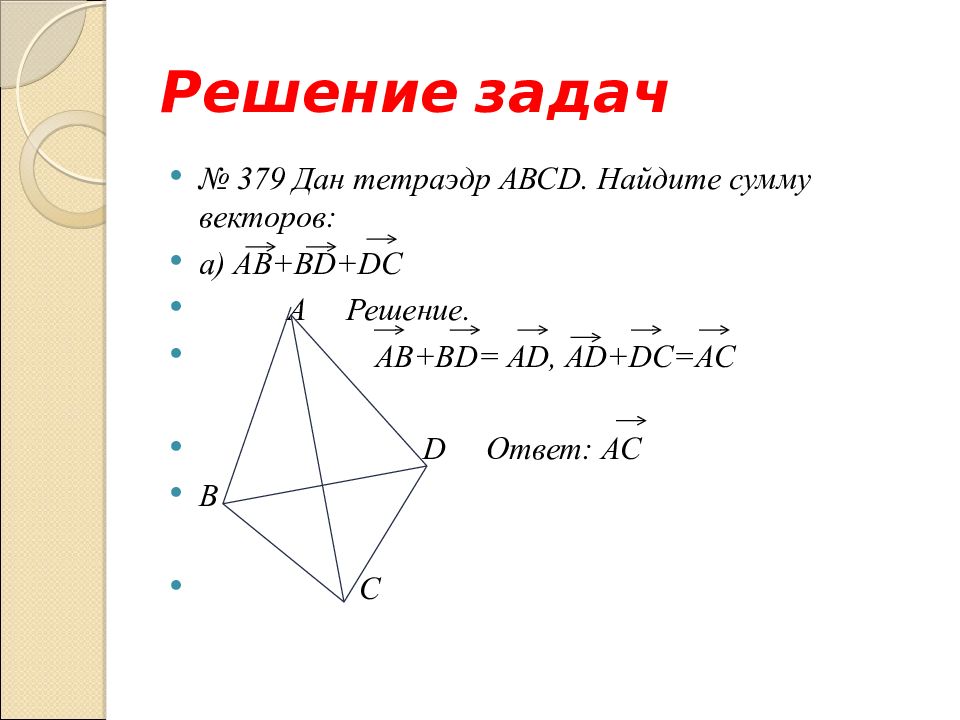
№ 379 Дан тетраэдр АВС D. Найдите сумму векторов: а) АВ+В D+DC
Слайд 9: Решение задач
№ 379 Дан тетраэдр АВС D. Найдите сумму векторов: а) АВ+В D+DC A D B C
Слайд 10: Решение задач
№ 379 Дан тетраэдр АВС D. Найдите сумму векторов: а) АВ+В D+DC A Решение. AB+BD= AD, AD+DC=AC D Ответ: АС B C
Слайд 11: Решение задач
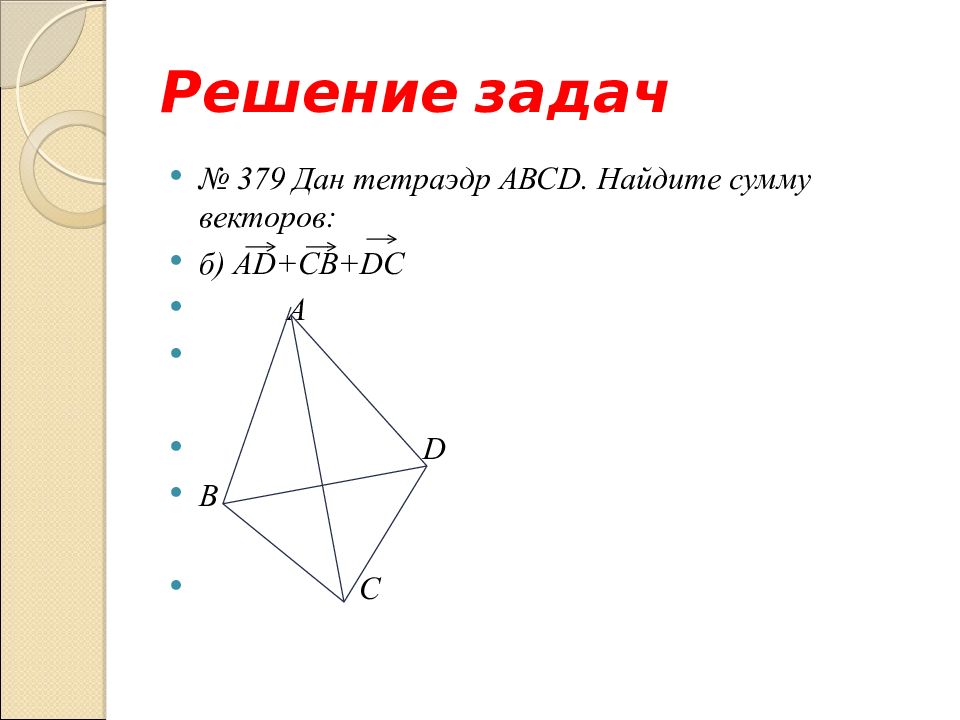
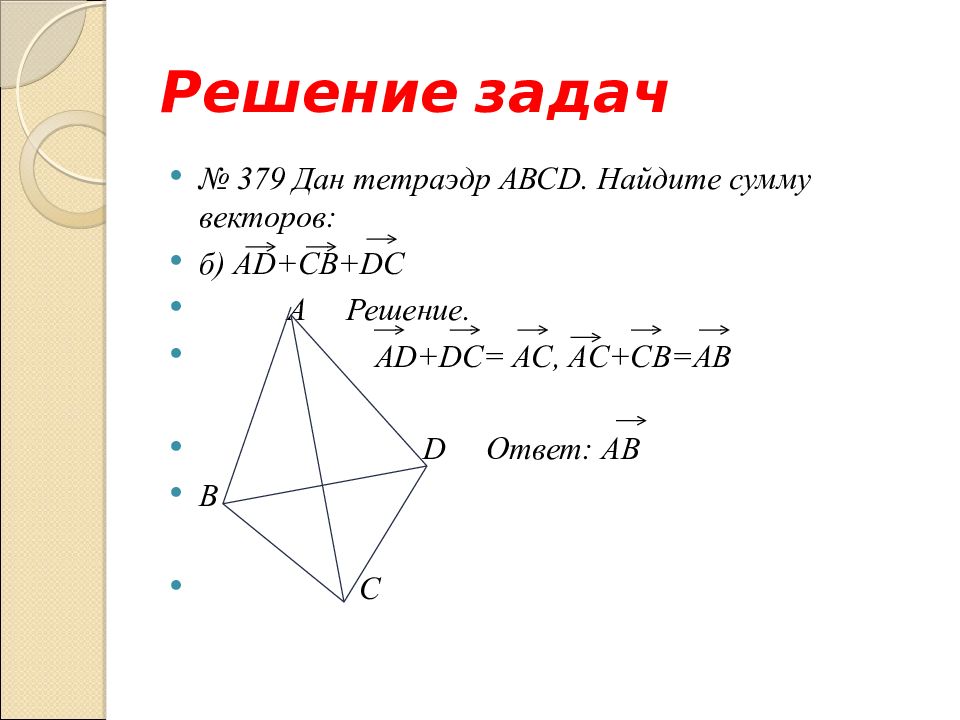
№ 379 Дан тетраэдр АВС D. Найдите сумму векторов: б) А D + C В +DC
Слайд 12: Решение задач
№ 379 Дан тетраэдр АВС D. Найдите сумму векторов: б) А D + C В +DC A D B C
Слайд 13: Решение задач
№ 379 Дан тетраэдр АВС D. Найдите сумму векторов: б) А D + C В +DC A Решение. AD+DC= AC, AC+CB=AB D Ответ: А B B C
Слайд 14: Решение задач
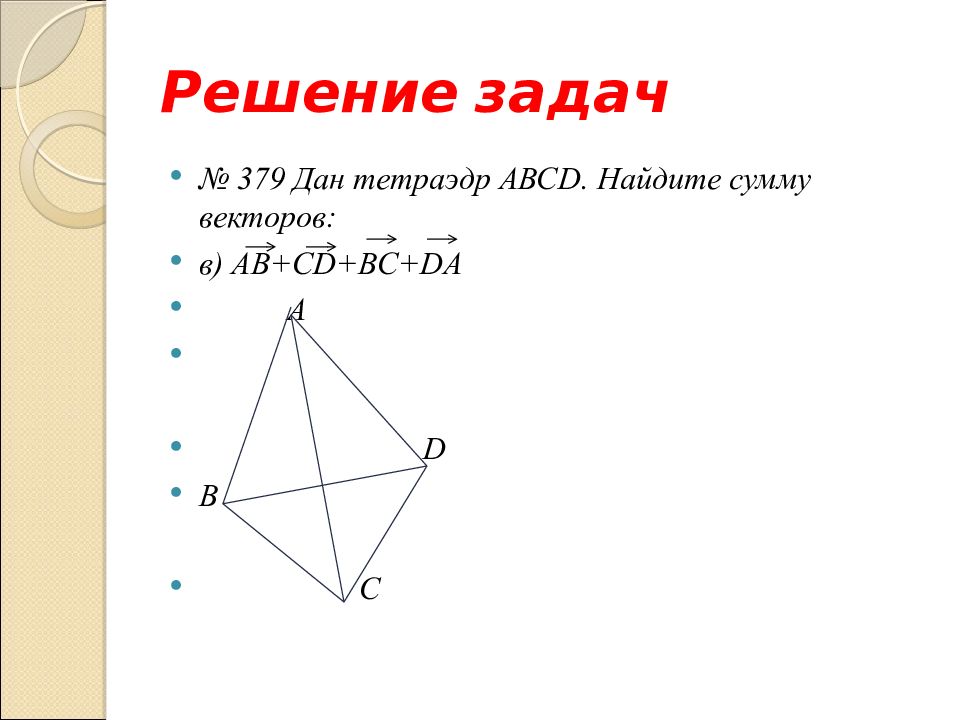
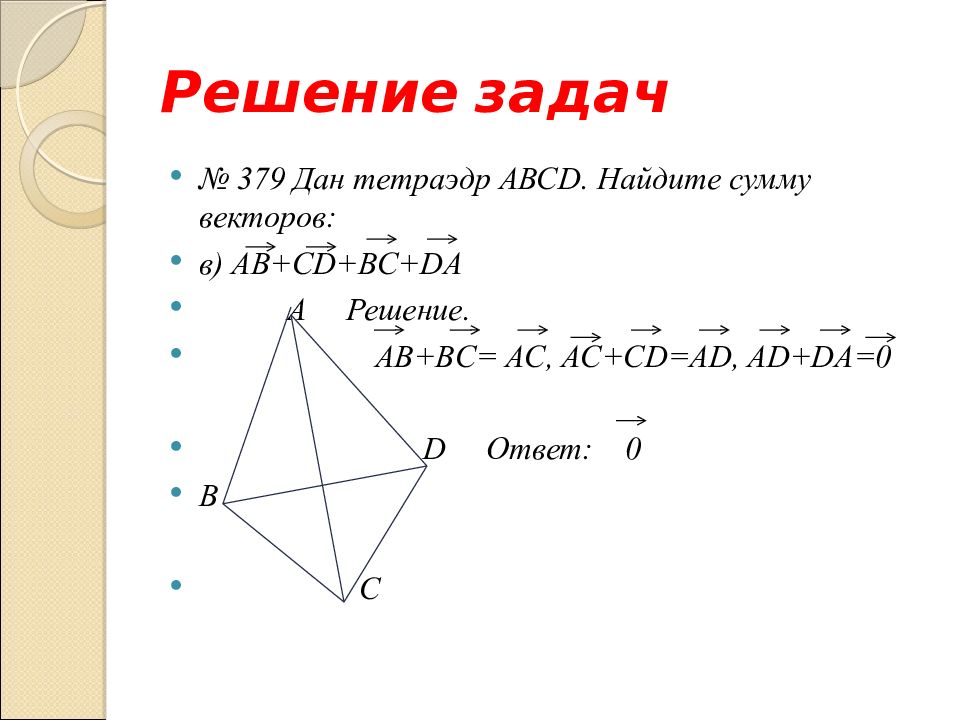
№ 379 Дан тетраэдр АВС D. Найдите сумму векторов: в) А B + CD+BC+DA
Слайд 15: Решение задач
№ 379 Дан тетраэдр АВС D. Найдите сумму векторов: в) А B + CD+BC+DA A D B C
Слайд 16: Решение задач
№ 379 Дан тетраэдр АВС D. Найдите сумму векторов: в) А B + CD+BC+DA A Решение. AB+BC= AC, AC+CD=AD, AD+DA=0 D Ответ: 0 B C
Слайд 17: Решение задач
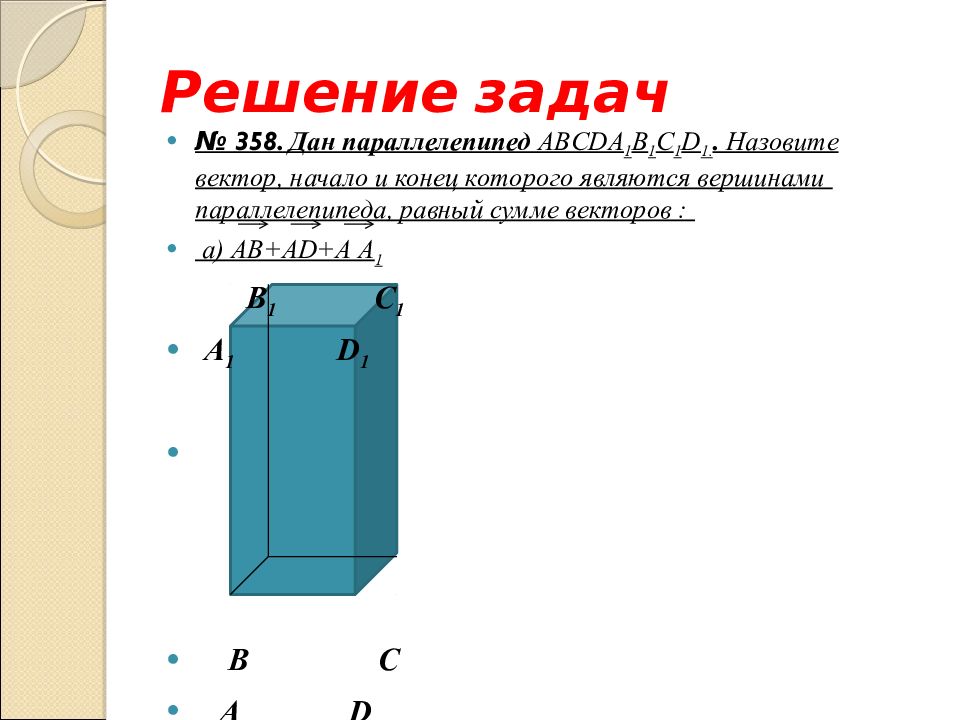
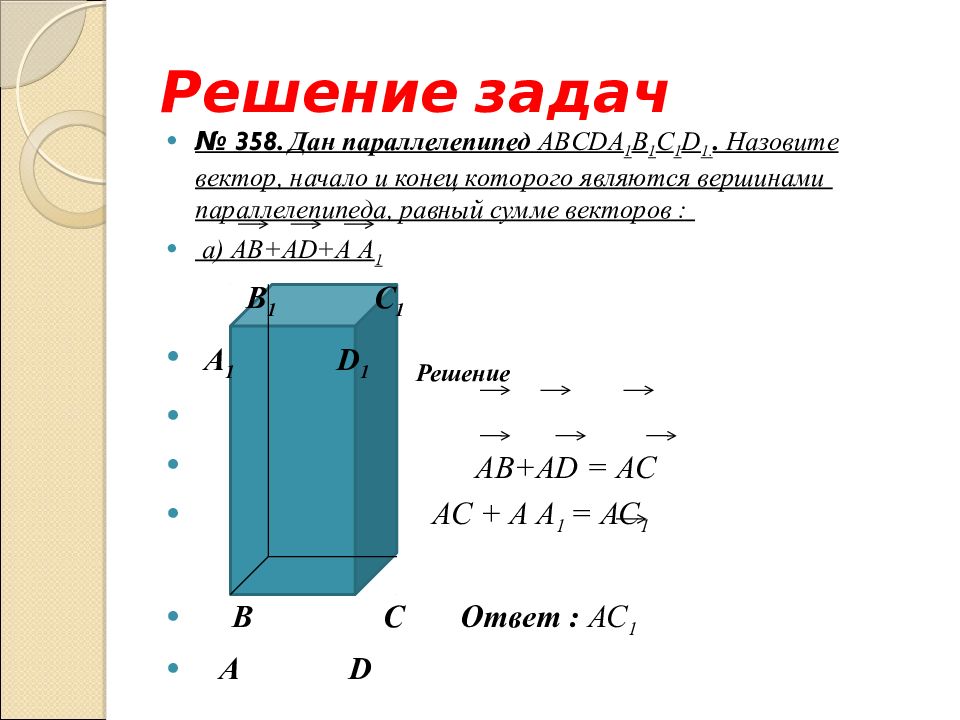
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : а) AB+AD+A А 1
Слайд 18: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : а) AB+AD+A А 1 B 1 С 1 А 1 D 1 B С А D
Слайд 19: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : а) AB+AD+A А 1 B 1 С 1 А 1 D 1 Решение AB+AD = АС АС + A А 1 = АС 1 B С Ответ : АС 1 А D
Слайд 20: Решение задач
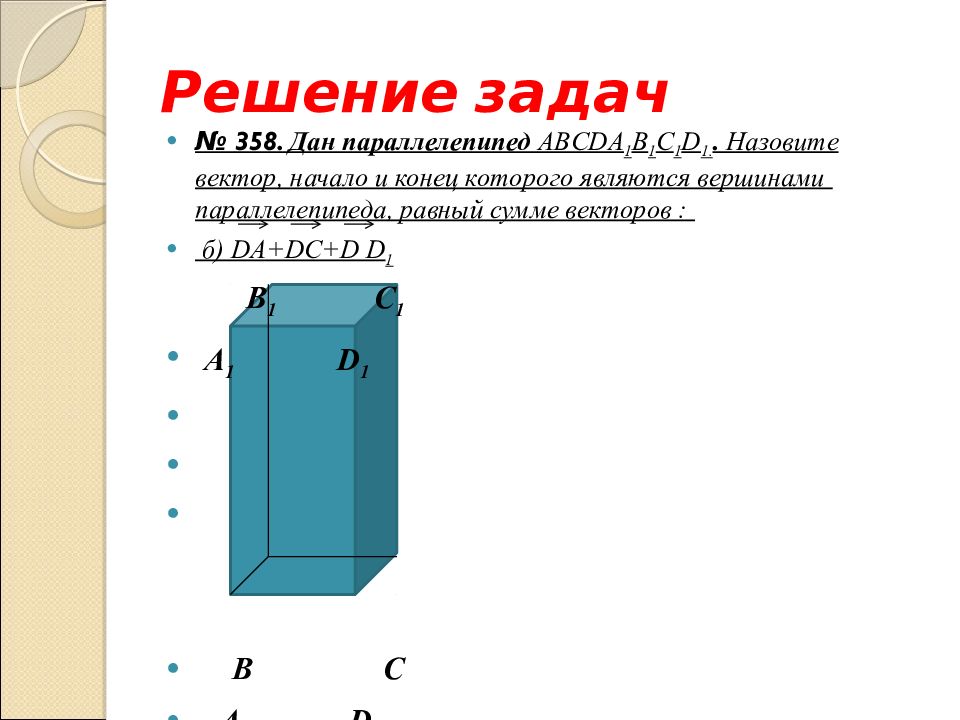
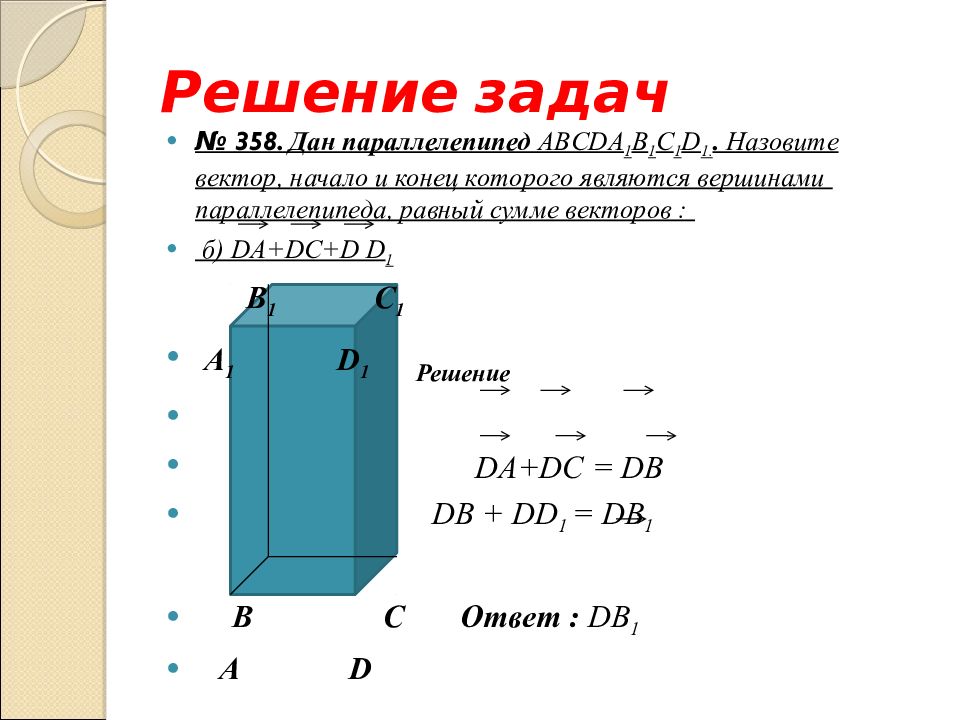
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : б) DA+DC+D D 1
Слайд 21: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : б) DA+DC+D D 1 B 1 С 1 А 1 D 1 B С А D
Слайд 22: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : б) DA+DC+D D 1 B 1 С 1 А 1 D 1 Решение DA+DC = DB DB + DD 1 = DB 1 B С Ответ : DB 1 А D
Слайд 23: Решение задач
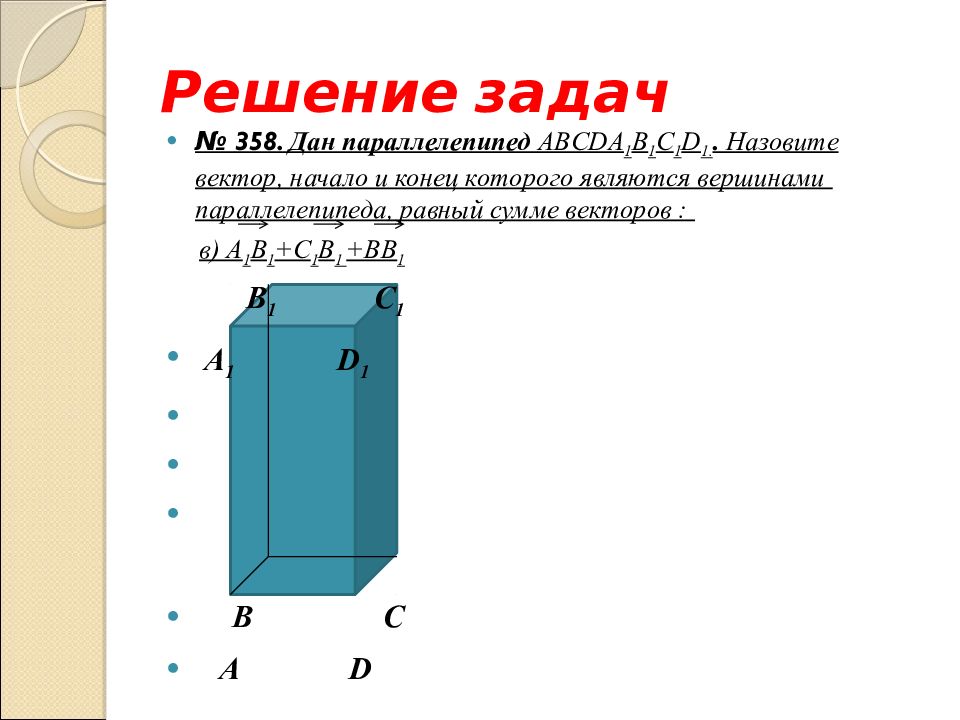
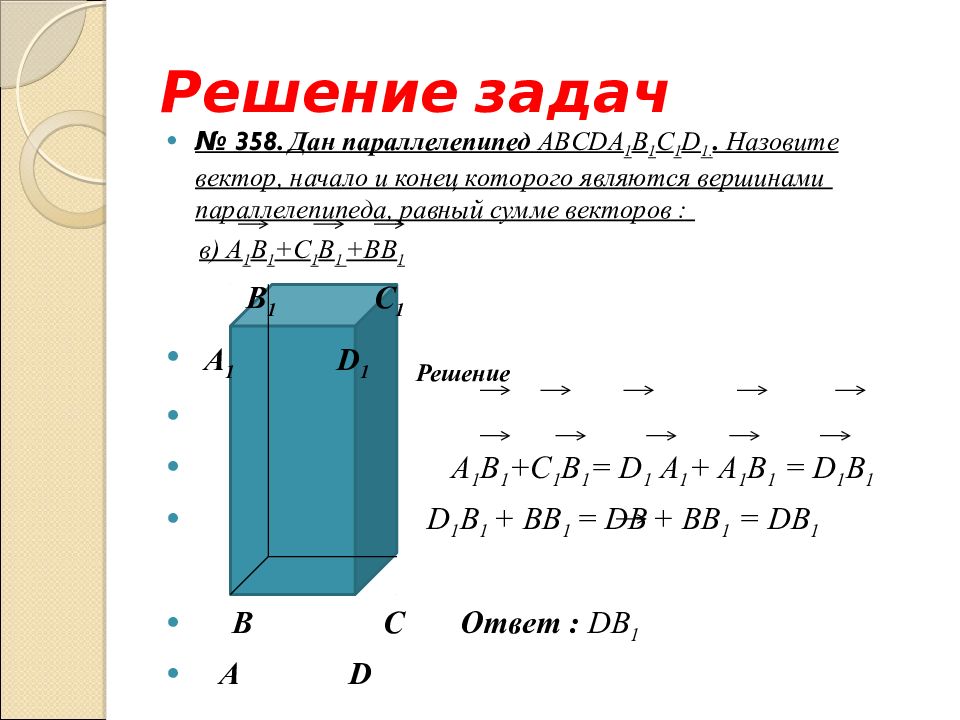
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : в) А 1 B 1 + С 1 B 1 + ВВ 1
Слайд 24: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : в) А 1 B 1 + С 1 B 1 + ВВ 1 B 1 С 1 А 1 D 1 B С А D
Слайд 25: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : в) А 1 B 1 + С 1 B 1 + ВВ 1 B 1 С 1 А 1 D 1 Решение А 1 B 1 + С 1 B 1 = D 1 А 1 + А 1 B 1 = D 1 В 1 D 1 В 1 + ВВ 1 = D В + ВВ 1 = DB 1 B С Ответ : DB 1 А D
Слайд 26: Решение задач
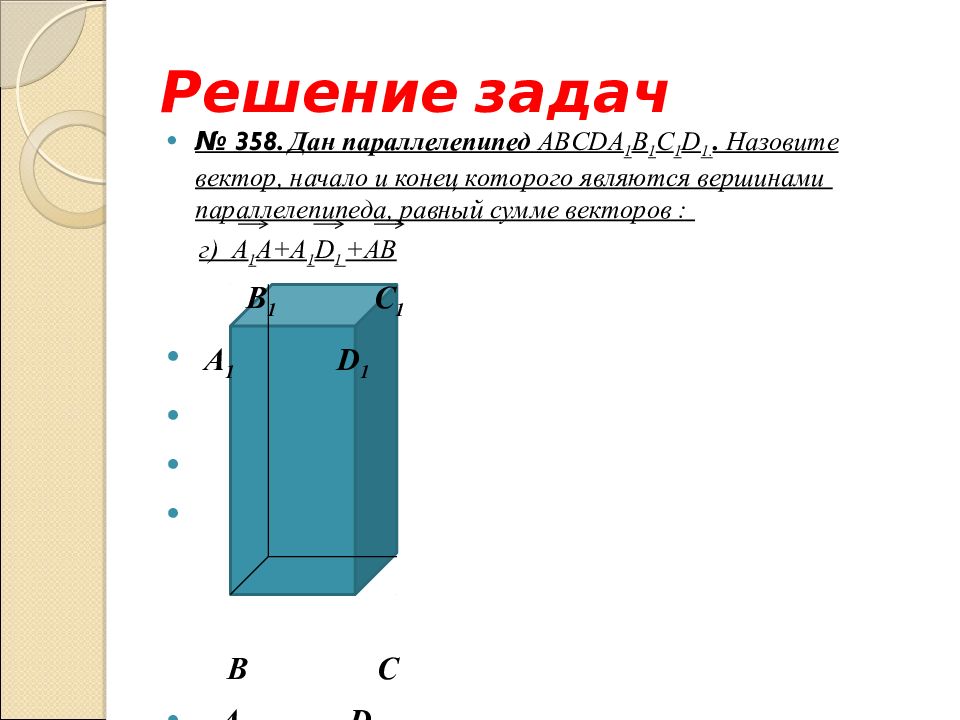
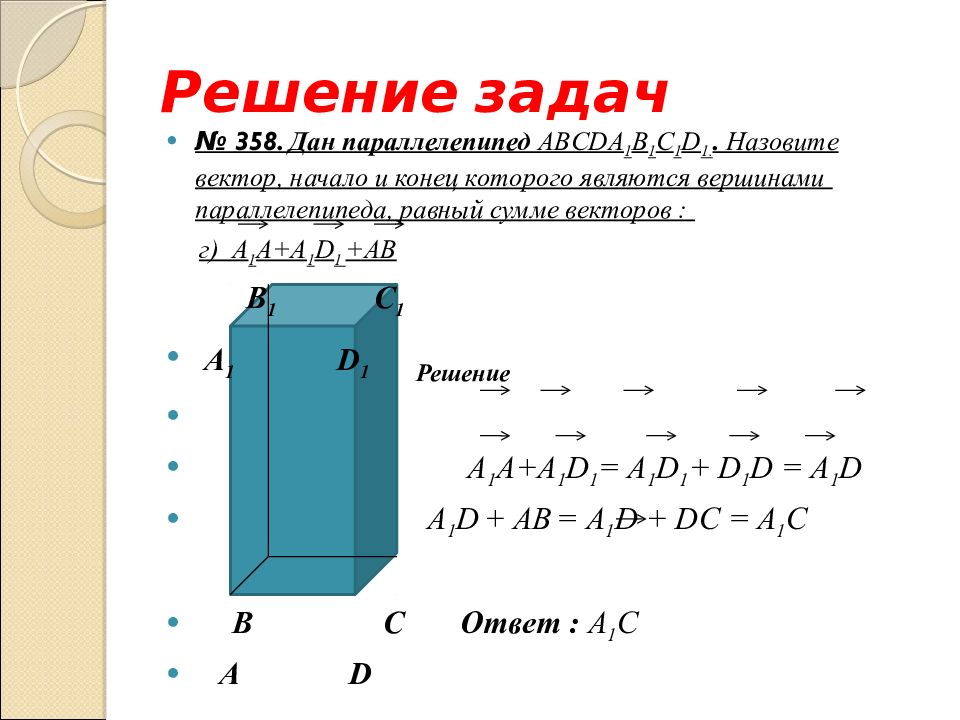
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : г) A 1 A+A 1 D 1 +A В
Слайд 27: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : г) А 1 А +A 1 D 1 +A В B 1 С 1 А 1 D 1 B С А D
Слайд 28: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : г) А 1 А +A 1 D 1 +A В B 1 С 1 А 1 D 1 Решение А 1 A+A 1 D 1 = A 1 D 1 + D 1 D = A 1 D A 1 D + A В = A 1 D + DC = A 1 C B С Ответ : A 1 C А D
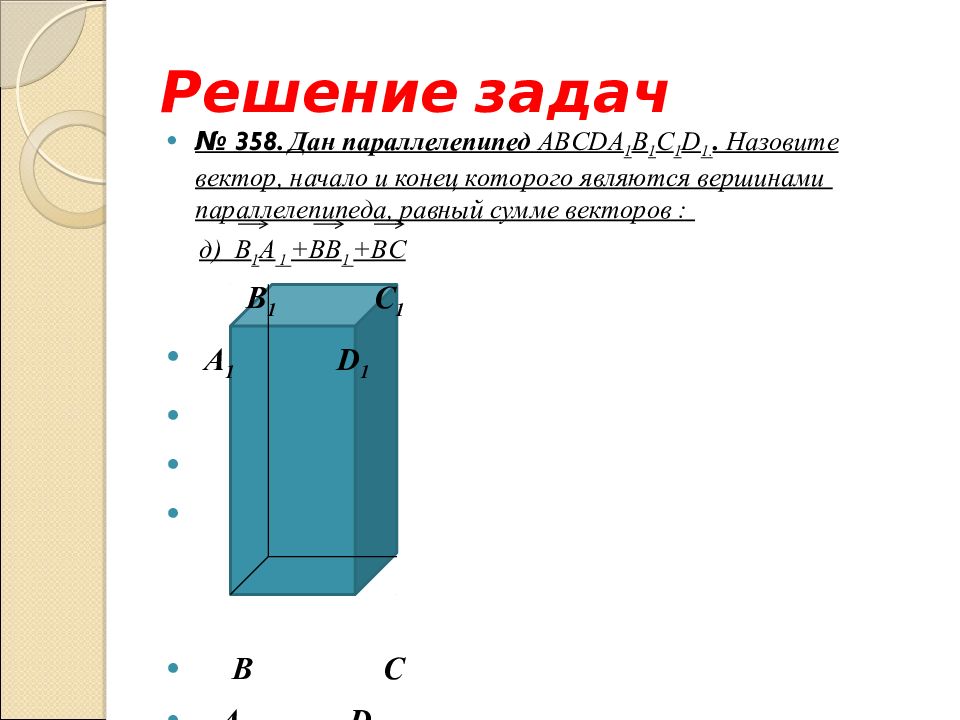
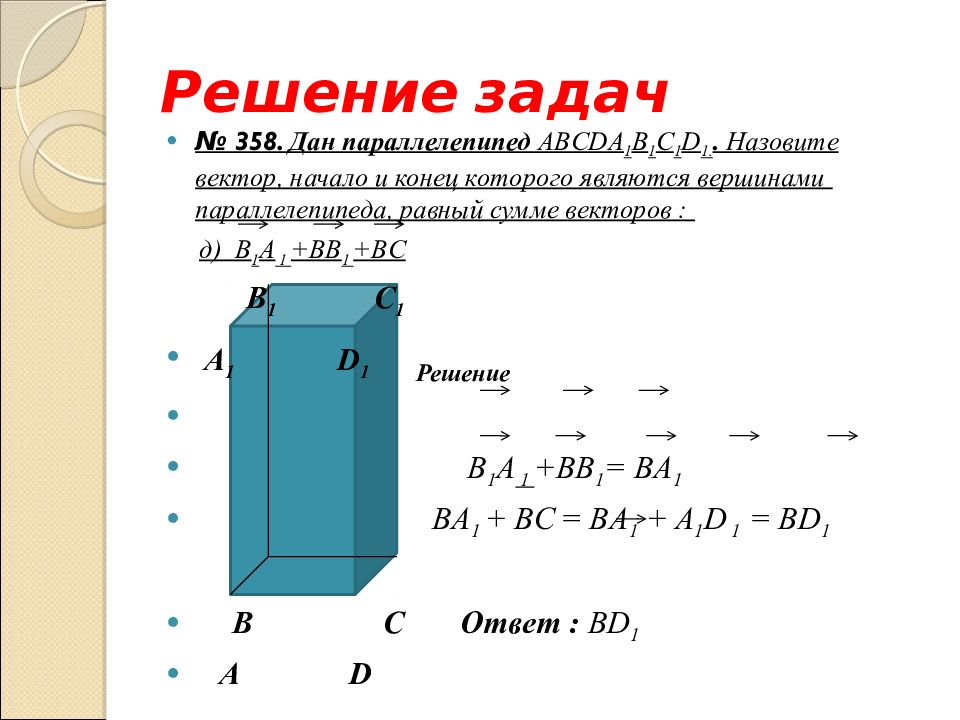
Слайд 29: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : в) B 1 A 1 +BB 1 + В C
Слайд 30: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : д) B 1 А 1 +BB 1 +BC B 1 С 1 А 1 D 1 B С А D
Слайд 31: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : д) B 1 А 1 +BB 1 +BC B 1 С 1 А 1 D 1 Решение B 1 A 1 +BB 1 = BA 1 BA 1 + В C = BA 1 + A 1 D 1 = BD 1 B С Ответ : BD 1 А D
Слайд 32: Решение задач
№ 358. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов : в) B 1 A 1 +BB 1 + В C
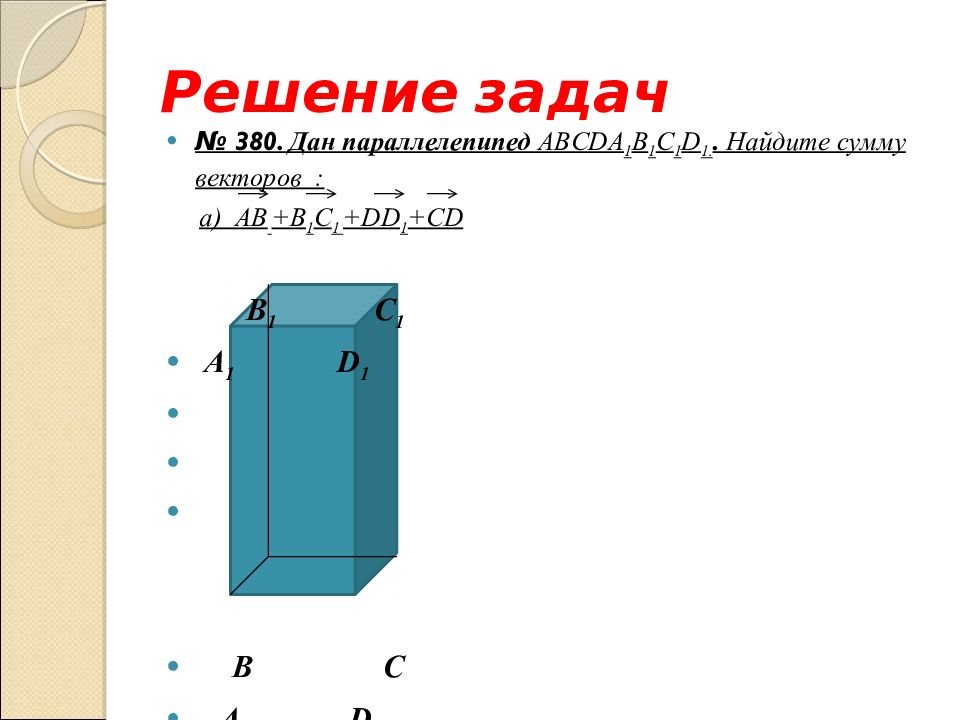
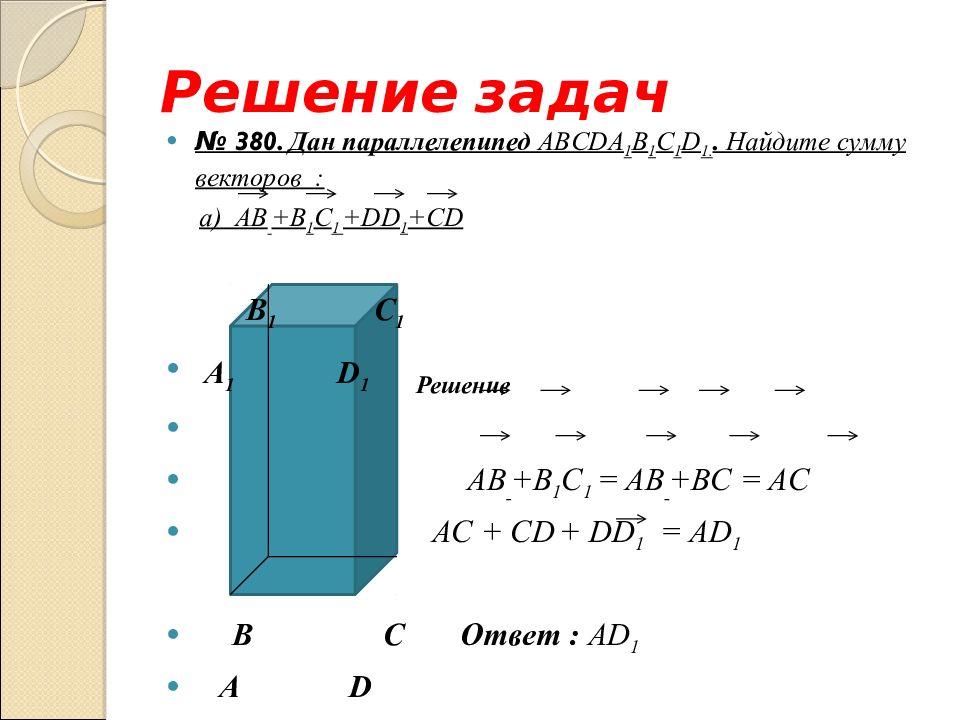
Слайд 33: Решение задач
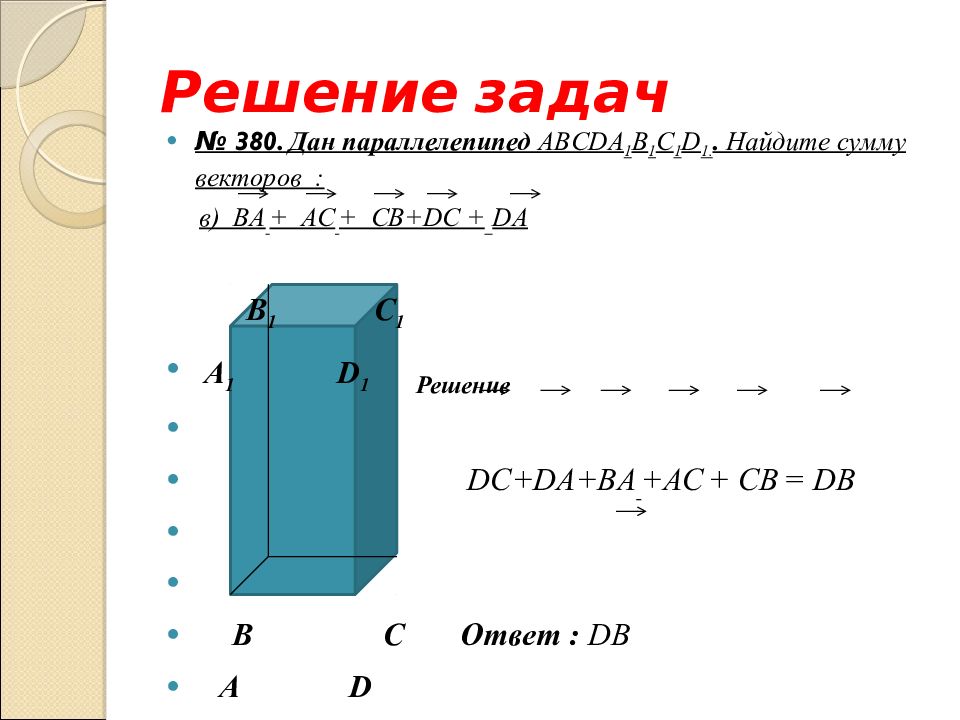
№ 380. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Найдите сумму векторов : а) А B +B 1 C 1 +DD 1 +CD B 1 С 1 А 1 D 1 B С А D
Слайд 34: Решение задач
№ 380. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Найдите сумму векторов : а) А B +B 1 C 1 +DD 1 +CD B 1 С 1 А 1 D 1 Решение AB +B 1 C 1 = AB +BC = AC AC + CD + DD 1 = AD 1 B С Ответ : AD 1 А D
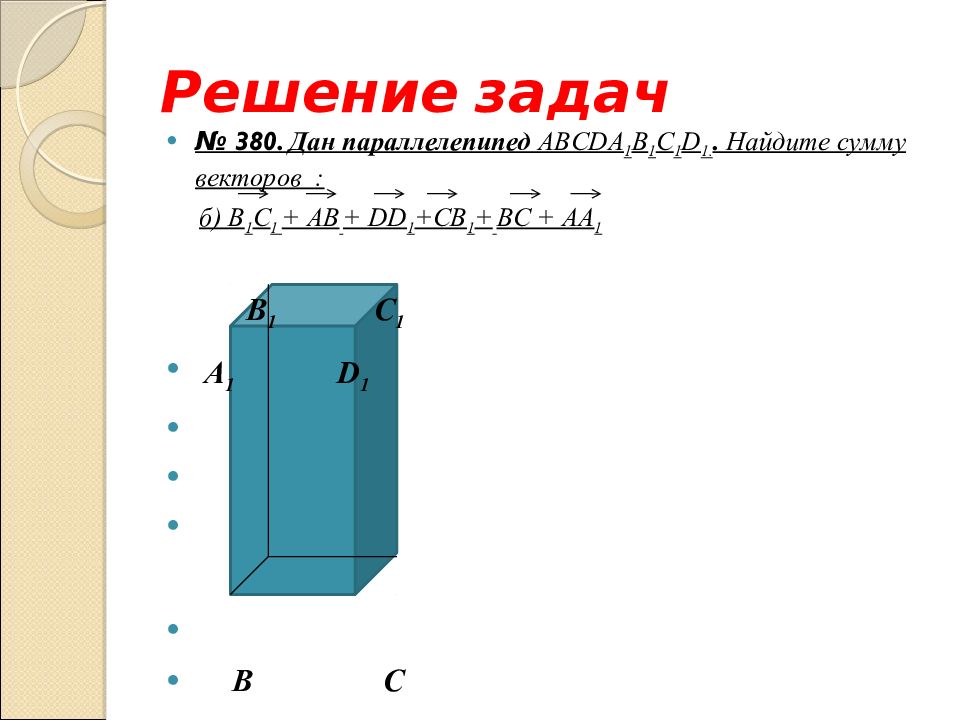
Слайд 35: Решение задач
№ 380. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Найдите сумму векторов : б ) B 1 C 1 + А B + DD 1 +CB 1 + BC + AA 1 B 1 С 1 А 1 D 1 B С А D
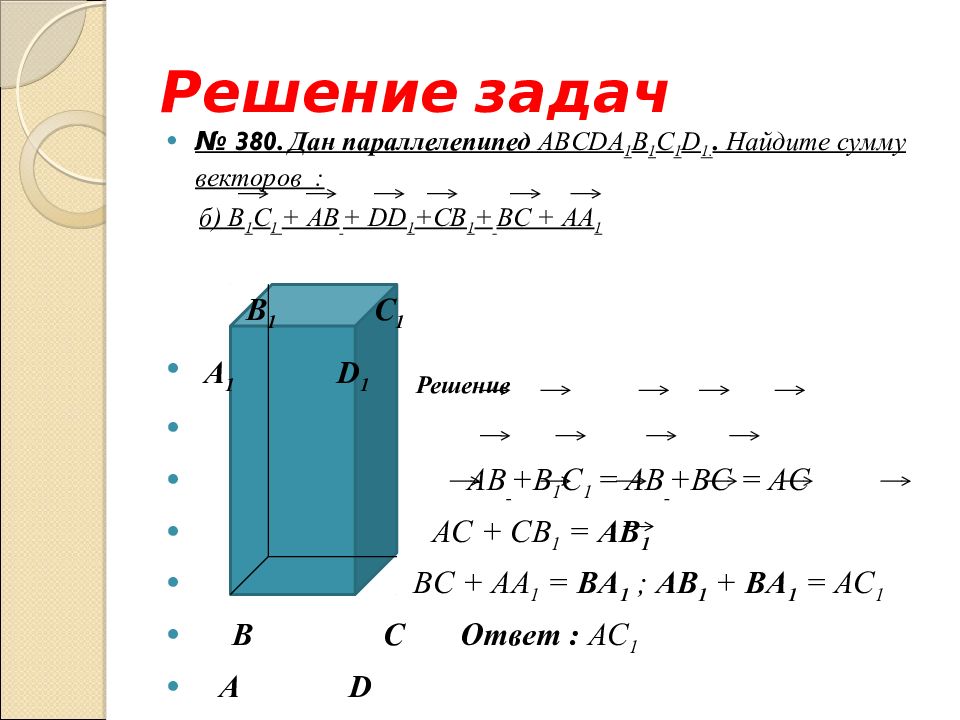
Слайд 36: Решение задач
№ 380. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Найдите сумму векторов : б ) B 1 C 1 + А B + DD 1 +CB 1 + BC + AA 1 B 1 С 1 А 1 D 1 Решение AB +B 1 C 1 = AB +BC = AC AC + CB 1 = AB 1 BC + AA 1 = BA 1 ; AB 1 + BA 1 = AC 1 B С Ответ : A С 1 А D
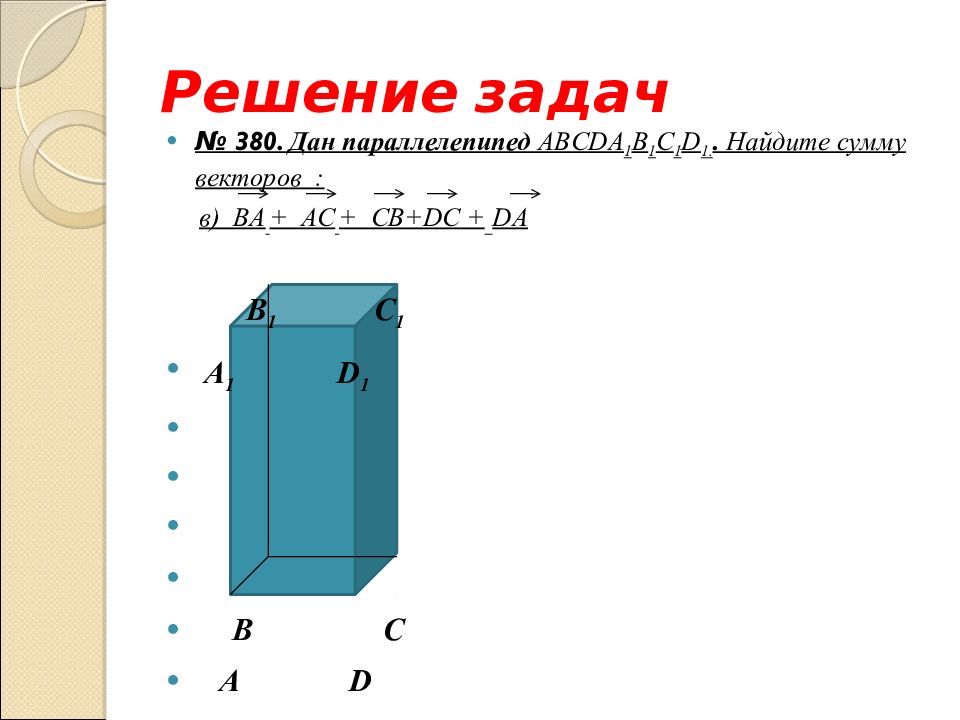
Слайд 37: Решение задач
№ 380. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Найдите сумму векторов : в ) B А + А C + CB+DC + DA B 1 С 1 А 1 D 1 B С А D
Слайд 38: Решение задач
№ 380. Дан параллелепипед ABCD А 1 B 1 С 1 D 1.. Найдите сумму векторов : в ) B А + А C + CB+DC + DA B 1 С 1 А 1 D 1 Решение DC+DA+BA +AC + CB = DB B С Ответ : DB А D
Слайд 39: Решение задач
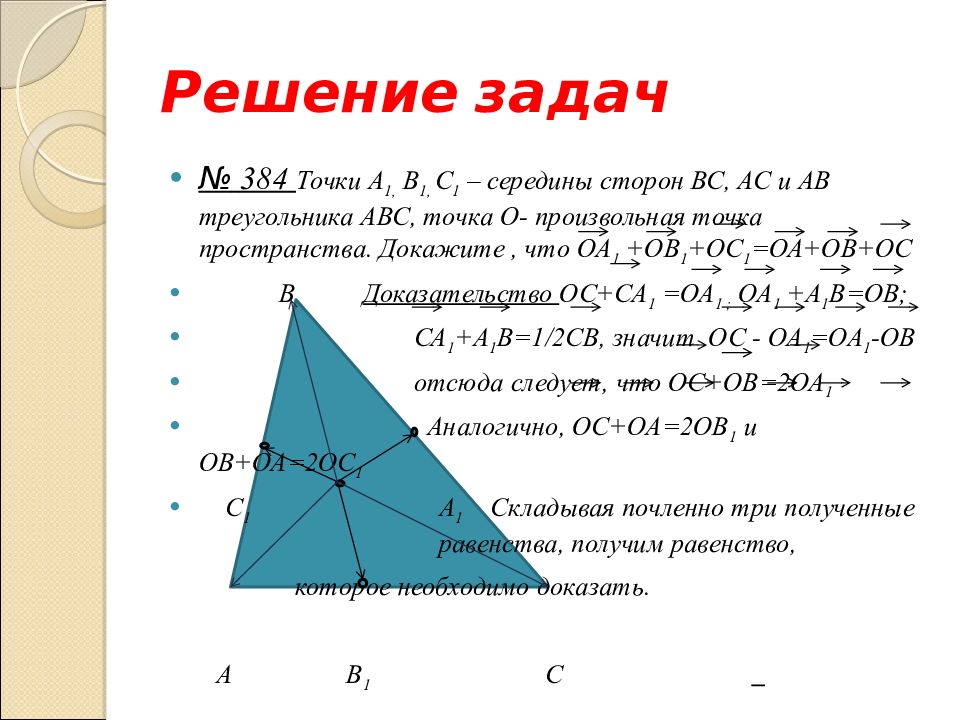
№ 384 Точки А 1, B 1, С 1 – середины сторон ВС, АС и АВ треугольника АВС, точка О- произвольная точка пространства. Докажите, что ОА 1 + ОВ 1 +ОС 1 =ОА+ОВ+ОС
Слайд 40: Решение задач
№ 384 Точки А 1, B 1, С 1 – середины сторон ВС, АС и АВ треугольника АВС, точка О- произвольная точка пространства. Докажите, что ОА 1 +ОВ 1 +ОС 1 =ОА+ОВ+ОС В С 1 А 1 А В 1 С
Последний слайд презентации: Работа по геометрии: Решение задач
№ 384 Точки А 1, B 1, С 1 – середины сторон ВС, АС и АВ треугольника АВС, точка О- произвольная точка пространства. Докажите, что ОА 1 +ОВ 1 +ОС 1 =ОА+ОВ+ОС В Доказательство ОС+СА 1 =ОА 1 ; ОА 1 +А 1 В=ОВ; СА 1 +А 1 В=1/2СВ, значит ОС - ОА 1 =ОА 1 -ОВ отсюда следует, что ОС+ОВ=2ОА 1 Аналогично, ОС+ОА=2ОВ 1 и ОВ+ОА=2ОС 1 С 1 А 1 Складывая почленно три полученные равенства, получим равенство, которое необходимо доказать. А В 1 С