А. А. Разборов Чикагский Университет Математический Институт им. Стеклова Семинар отдела мат. о снов ИИ, 19 Июня 2024 г. О вопросах сходимости и генерализации нейронных сетей малой глубины
I. Виды машинного обучения Supervised learning Agnostic learning Unsupervised/semi-supervised learning Generative learning (transformers, ChatGPT etc.) Reinforcement learning Etc.
II. Функции ошибок
III. Обучение и тестирование Статистическая теория
б ) Бенчмарки Оказывается, что по большому счёту разница между этими двумя моделями невелика. Статистическая теория, популяционная ошибка
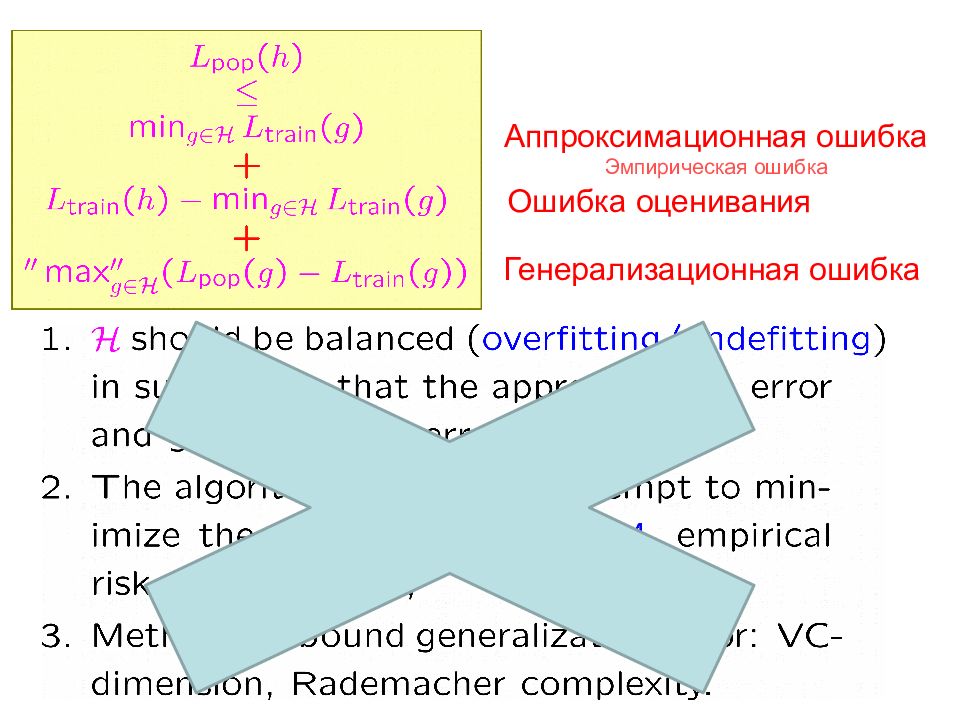
Аппроксимационная ошибка Ошибка оценивания Генерализационная ошибка Классическая теория ( underfitting / overfitting ): Эмпирическая ошибка
IV. В эпоху нейронных сетей... 3. ??? Fantastic Generalization Measures and Where to Find Them [Jiang Neyshabur Mobahi Krishan Bengio 20]
Класс г ипотез: полносвязные схемы глубины 2
Алгоритм: (стохастический) градиентный спуск/поток Инициализация (одна из возможных) Градиентный спуск Градиентный поток
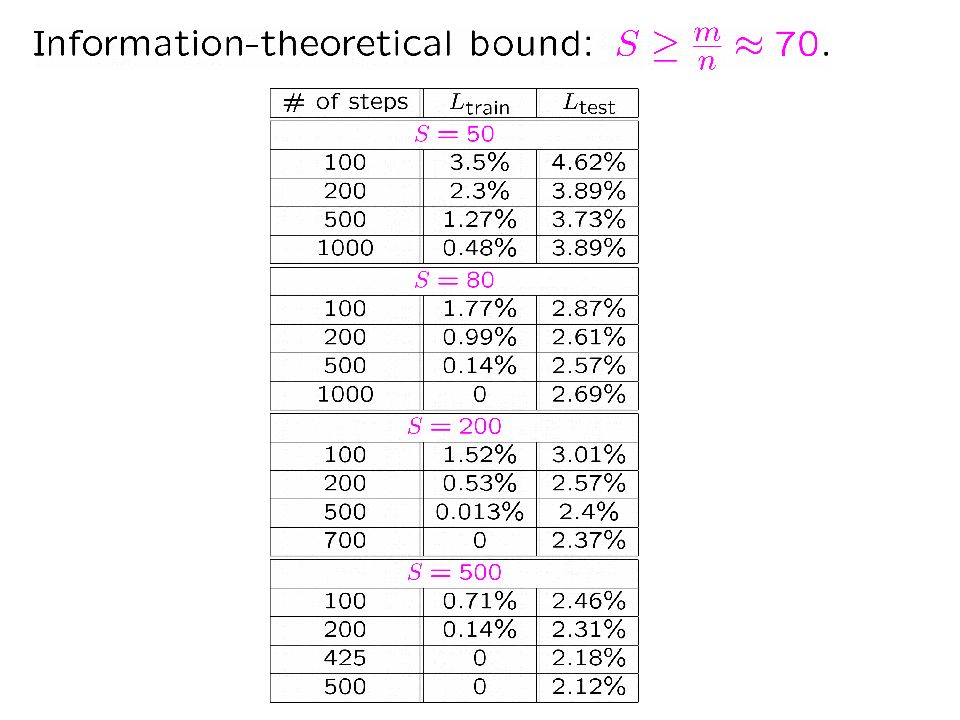
Эксперименты ( довольно примитивные ) MNIST – простейшая ( и одна из самых популярных ) баз данных, состоящая из рукописных цифр [ Bottou et al. 94]. Использовалась в [Hinton Osindero Teh 06].
Теоретическое объяснение генерализации предполагает : В чём состоит специфика исходных данных ? “ Ёмкость ” ( capacity ) градиентного спуска. Cat1 airplane, cat2 dog etc. [Zhang Bengio Hardt Recht Vinyals 17, 21]: при случайном выборе меток сходимость ( при тех же параметрах ) сохраняется … Но, возможно, дело в том, что она становится существенно более медленной ? [ Arora Du Hu Li Wang 19]
Одна попытка объяснения : пройденное расстояние [Li Liang 18, Allen-Zhu Li Song 19, Arora Du Hu Li Wang 19] Ёмкость Большой градиент быстрая сходимость. Большой градиент малое смещение Rademacher generalization.
Сходимость
Градиентный спуск / поток сходится к критической точке ( нулевой градиент ), но почему это глобальный ( или даже локальный ) минимум ? Quadratic loss in the error space, the dynamics is determined by a linear ODE
Агрессивный подход : Часть I: инициализация [ Oymak Soltanolkotabi 19, Arora Du Hu Li Salakhutdinov Wang 19, Nguyen Mondelli Montafar 21, Montanari Zhong 21, R 22] Часть I.I: предельный случай (NTK, Neural Tangent Kernel) [ Jacot Gabriel Hongler 18]
Часть I.II: сходимость к NTK [ADHLSW 19, MZ21] Вывод : ситуация при инициализации вполне удовлетворительна.
Часть II: от к Типичные результаты никак не зависят от меток ( ср. [Zhang Bengio Hardt Recht Vinyals 17, 21 ] ). Это снижает их ценно сть для изучения генерализации. Они относятся к так называемому NTK - режиму (lazy training). На практике обучение происходит далеко за его пределами. Число нейронов неоправданно велико. [ Du Zhai Pocsoz Singh 19, Wu Du Ward 19, Oymak Soltanolkotabi 19, Song Yang 20, Nguyen 21, R. 22 ] Критические замечания
Матриц а активации – формулы слегка упрощаются.
Общая стратегия доказательств Совместной индукцией по устанавливаются следующие ( взаимосвязанные !) факты. При этом используются различные свойства выборки выполняющиеся почти всюду. -- сравнительно просто [ Du Zhai Pocsoz Singh 19 ].
Главные условия Независимость от меток [R 22]
Некоторые частные случаи
Some Directions for Future (Label-Independent) Research Generalize known results to deeper networks (new layers of difficulties arise)... Going outside of the NTK regime (more intelligent ways to analyze the learning trajectory…) The first goal: go beyond the barrier To what extent are ``practical’’ data and databases (but not labels) quasi-random? Better unification of known results for regression vs. (multi)-classification or the feedforward archirecture vs. CNN/ Resnet etc.
Спасибо за внимание
