Первый слайд презентации: Раздел 4 Колебания и волны
Курс лекций по общей физики Доцент Петренко Л.Г. Кафедра общей и экспериментальной физики НТУ «ХПИ» Харьков - 2013 год
Слайд 2
Колебания - это процессы (движения или изменения состояния), имеющие различную физическую природу, в той или иной степени повторяющиеся во времени. В зависимости от физической природы колебательных процессов их разделяют на: 1) механические, 2) электромагнитные и 3) электромеханические. 5.1.1. Понятие о колебательных процессах. Единый подход к колебаниям различной физической природы. Характеристики гармонических колебаний: смещение от положения равновесия, амплитуда, период, линейная и циклические частоты, фаза, начальная фаза. 5. ФИЗИКА КОЛЕБАНИЙ И ВОЛН. ОПТИКА 5.1. КИНЕМАТИКА СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР Механические колебания совершают маятники, струны, пружины. Механическими являются колебания давления в упругой среде, в которой распространяются звук или сейсмические колебания.
Слайд 3
Электромеханические колебания совершают мембраны громкоговорителей, телефонов, микрофонов, слуховых аппаратов. Электромагнитные колебания совершают напряжение и сила тока в электрических сетях и колебательных контурах электрических систем, электромагнитное поле при распространении света, радиосигналов. Все эти колебания обусловлены двумя из четырёх фундаментальных взаимодействий в природе - гравитационным и электромагнитным.
Слайд 4
Периодическими называются колебания, при которых значения всех физических величин, характеризующих систему и изменяющихся при колебаниях, повторяются через равные промежутки времени, наименьший из которых называется периодом колебаний ( Т ). Тела или системы тел, способные без внешнего воздействия совершать колебания, называются колебательными системами. Колебания, совершаемые без внешнего воздействия, называются свободными. Переменное внешнее воздействие обуславливает возникновение в колебательной системе вынужденных колебаний. Математический аппарат, описывающий все виды колебательных процессов, является общим. Независимо от физической природы колебаний, они описываются одинаковыми уравнениями и аналогичными параметрами. Это позволяет широко использовать аналогии - закономерности, полученные при изучении колебаний одного вида, переносить на другой вид.
Слайд 5
Здесь S ( t ) - смещение или отклонение физической величины S от равновесного значения в момент времени t, = 2 /Т = 2 - циклическая (угловая) частота, = 1/Т - линейная частота, S 0 - амплитуда колебаний, равная максимальному значению колеблющейся величины, ( t ) = t + 0 - фаза колебаний, представляющая собой аргумент периодически изменяющейся функции, описывающей колебательный процесс, 0 = (0) - начальная фаза колебаний, определяющая фазу в начальный момент времени. Простейшими являются гармонические или синусоидальные колебания, при которых колеблющаяся физическая величина S (безразлично механическая или электромагнитная) изменяется со временем по гармоническому, т.е. синусоидальному закону : S ( t ) = S 0 sin ( t ) = S 0 sin ( t + 0 ) = S 0 cos ( t + 0 * ) ( 0 * = 0 - /2).
Слайд 6
Очевидно, что S ( t ) = S ( t + Т) = S ( t + n Т), где n = 1,2,3.... Если колебательное движение может быть описано периодической (но не гармонической) функцией f(t) с частотой ω, то, пользуясь математическим методом разложения функций в ряд Фурье, можно её представить в виде: то есть в виде ряда гармонических функций с частотами n ω, кратными основной частоте, и амплитудами А n, где n =1,2,3… - номер гармоники. Гармонические колебания достаточно широко распространены в природе. Всякий периодический процесс можно представить как наложение большего или меньшего числа гармонических колебаний (гармоник). Математически это выражается в разложении периодической функции, описывающей колебательный процесс, в ряд Фурье.
Слайд 7
5.1.2. Скорость и ускорение точки, совершающей гармонические колебания. Быстрота изменения смещения со временем, т.е. производная от гармонической функции S ( t ) по времени, также изменяется по гармоническому закону : При механических колебаниях эта величина есть скорость движения колеблющейся точки, т.е. где v 0 = S 0 - амплитуда скорости. При механических колебаниях эта величина есть ускорение точки, т.е. . ; v(t) = - S 0 . sin( t + 0 ) = - v 0. sin( t + 0 ) = v 0. cos( t + 0 + π/2) Быстрота изменения скорости, т.е. вторая производная от гармонической функции S ( t ) по времени, также изменяется по гармоническому закону : , а (t) = - S 0 2. cos( t + 0 ) = - a 0 cos( t + 0 ) = a 0 cos( t + 0 + ) где а 0 = S 0 2 - амплитуда ускорения. . ,
Слайд 8
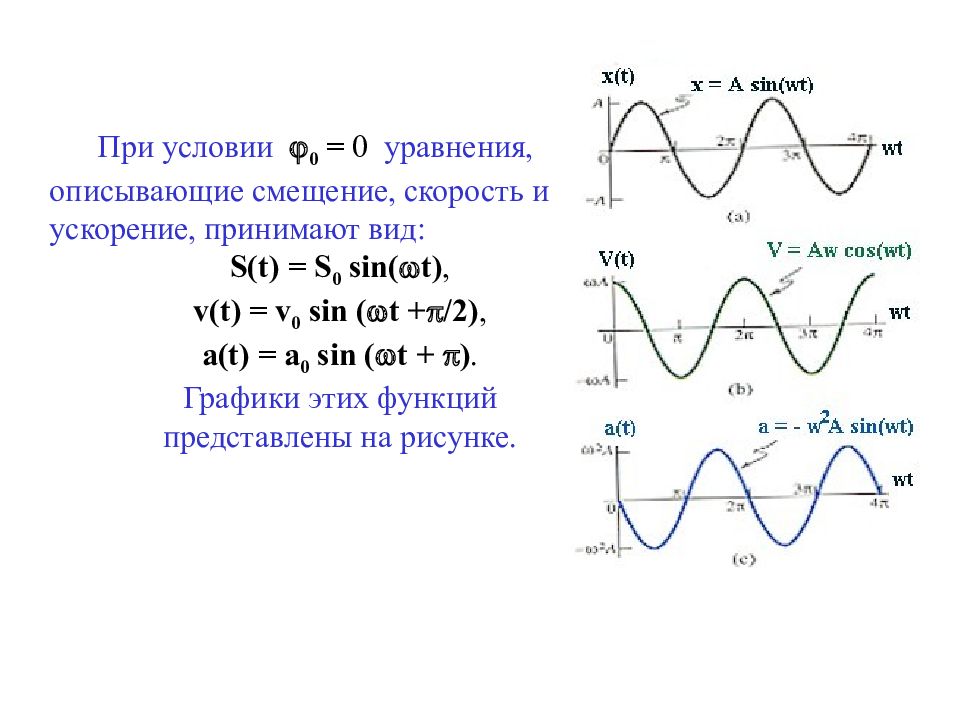
При условии 0 = 0 уравнения, описывающие смещение, скорость и ускорение, принимают вид: S(t) = S 0 sin( t), v(t) = v 0 sin ( t + /2 ), а( t ) = a 0 sin ( t + ). Графики этих функций представлены на рисунке.
Слайд 9
5.1.3. Графический способ представления колебаний с помощью вращающегося вектора. Комплексная форма представления колебаний. Гармонические колебания удобно сопоставлять с движением точки по окружности - проекция этой точки на любую прямую, проведенную через центр окружности, совершает гармоническое колебание около этого центра с частотой, равной угловой скорости движения точки по окружности. Выбирается горизонтальная ось Х, называемая опорной линией. Из некоторой точки О на этой линии проводится вектор, называемый вектором амплитуды, модуль которого равен амплитуде S 0, направленный под углом, равным начальной фазе колебаний 0, к опорной линии. Вектор амплитуды равномерно вращается против часовой стрелки с угловой скоростью, равной циклической частоте колебаний. В момент времени t вектор амплитуды составляет с осью Х угол, равный фазе колебаний ( t ) = t + 0. Соответственно, проекция вектора на ось Х совершает колебания по гармоническому закону : S ( t ) = S 0 cos ( t + 0 ). Описанный метод называется методом векторных диаграмм.
Слайд 10
При решении некоторых задач в теории колебаний удобнее пользоваться не тригонометрической, а комплексной формой записи уравнений колебаний. Для этого необходимо воспользоваться формулами Эйлера : Здесь i = - мнимая единица. Комплексная форма записи гармонического колебания имеет вид: где - комплексная амплитуда колебаний. Физический смысл имеют только отдельно действительная и мнимая части комплексного уравнения.
Слайд 11
5.1.4. Сложение скалярных и векторных колебаний. Сложение гармонических колебаний одного направления. Векторные диаграммы. Биения. Одной из фундаментальных задач теории колебаний является задача нахождения уравнения движения, являющегося суперпозицией двух или нескольких гармонических скалярных или векторных колебаний. Сложение векторных колебаний всегда можно свести к сложению колебаний одного направления и взаимно перпендикулярных колебаний. Рассмотрим задачу о сложении двух гармонических колебаний одинаковой частоты и одного направления (сложение скалярных колебаний или сложение колебаний двух коллинеарных векторов). Уравнения этих колебаний имеют вид: Уравнение результирующего колебания представляет собой сумму: Задача нахождения функции S(t) решается методом векторных диаграмм.
Слайд 12
На рисунке представлены векторы амплитуды и. Поскольку циклическая частота складываемых колебаний одинакова, то и угловая скорость вращения векторов амплитуды также одинакова и равна . Поэтому форма параллелограмма, построенного на векторах и, и длина его диагонали не изменяются со временем. (1) Вектор амплитуды результирующего колебания совпадает с диагональю параллелограмма и вращается с той же угловой скоростью . Длина его не изменяется со временем и может быть определена по теореме косинусов :
Слайд 13
Фаза результирующего колебания равна: ( t ) = t + 0, а начальная фаза 0 может быть определена из векторной диаграммы: Таким образом, суперпозиция двух гармонических колебаний одинаковой частоты и одинакового направления есть гармоническое колебание того же направления и той же частоты, выражающееся формулой: (2) в которой амплитуда S 0 определяется формулой (1), а начальная фаза 0 - формулой (2). Главным результатом является то, что амплитуда результирующего колебания S 0 и его интенсивность I, пропорциональная квадрату амплитуды ( I S 0 2 ), не являются суммой амплитуд и интенсивностей составляющих колебаний, а существенным образом зависят от разности фаз складываемых колебаний.
Слайд 14
Частные случаи: = 2n , где n =1,2,3,... S 0 = S 01 + S 02 и I > I 1 + I 2 ; = (2n + 1) , где n =1,2,3,... S 0 = S 01 - S 02 и I < I 1 + I 2 ; = (2n + 1) /2, где n =1,2,3,... S 0 2 = S 01 2 + S 02 2 и I = I 1 + I 2. Этот вывод является предпосылкой к рассмотрению явления интерференции. Рассмотренные выше колебания являются когерентными. Когерентные колебания происходят согласовано во времени так, что разность их фаз остаётся постоянной. Гармонические колебания одинаковой частоты всегда когерентны. Гармонические колебания с разными частотами ( 1 2 ) - не когерентны, так как разность фаз складываемых колебаний непрерывно меняется. Векторы амплитуды и вращаются с разными скоростями, а построенный на них параллелограмм непрерывно деформируется. Результирующее колебание не является гармоническим. Особый интерес представляет сложение одинаково направленных гармонических колебаний с разными, но близкими частотами - | 1 - 2 |<< 1. Результирующие колебания являются негармоническими и называются биениями.
Слайд 15
Рассмотрим частный случай биений. Исходные колебания описываются уравнениями: причём << , амплитуды колебаний одинаковы, а начальные фазы равны 0. Уравнение результирующего колебания можно представить в виде: Частота = | 1 - 2 | называется частотой биений, а величина Т б =2 / называется периодом биений. Характер зависимости S ( t ) при биениях представлен на рисунке. Величина называется условной амплитудой биений и изменяется от 0 до 2 S 0 c циклической частотой 2 S 0 - 2 S 0
Слайд 16
5.1.5 Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу. Практическое применение сложения колебаний. Рассмотрим задачу о сложении взаимно перпендикулярных гармонических колебаний материальной точки М, происходящих вдоль осей ОХ и О Y с одинаковой частотой . Уравнения этих колебаний имеют вид: где х и y - декартовы координаты точки М. Эти уравнения представляют траекторию точки М в параметрическом виде (параметром является время t ). Для получения уравнения траектории в аналитическом виде необходимо из этих уравнений исключить параметр t. Это уравнение эллипса с неприведенными осями. Точка М описывает этот эллипс за время Т = 2 / . Результирующее движение точки М называют эллиптически поляризованным колебанием. Форма эллипса и ориентация его осей зависят от разности фаз складываемых колебаний и от их амплитуды.
Слайд 17
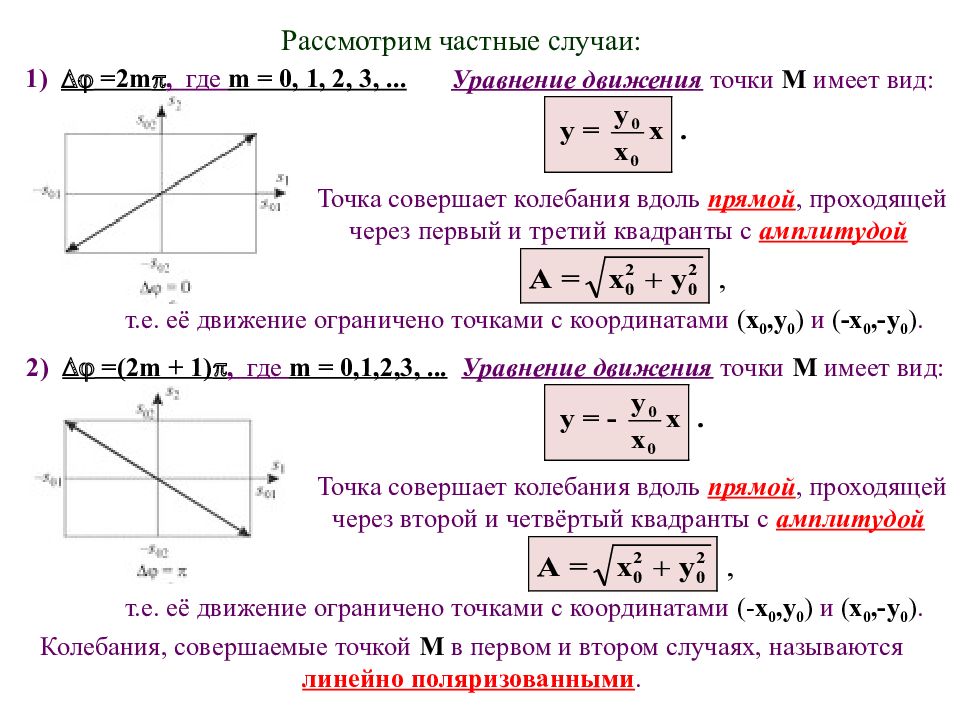
Рассмотрим частные случаи: 1) =2 m , где m = 0, 1, 2, 3,... Уравнение движения точки М имеет вид: Точка совершает колебания вдоль прямой, проходящей через первый и третий квадранты с амплитудой т.е. её движение ограничено точками с координатами ( x 0, y 0 ) и ( - x 0,- y 0 ). 2) =(2 m + 1) , где m = 0,1,2,3,... Уравнение движения точки М имеет вид: Точка совершает колебания вдоль прямой, проходящей через второй и четвёртый квадранты с амплитудой т.е. её движение ограничено точками с координатами (- x 0, y 0 ) и ( x 0,- y 0 ). Колебания, совершаемые точкой М в первом и втором случаях, называются линейно поляризованными.
Слайд 18
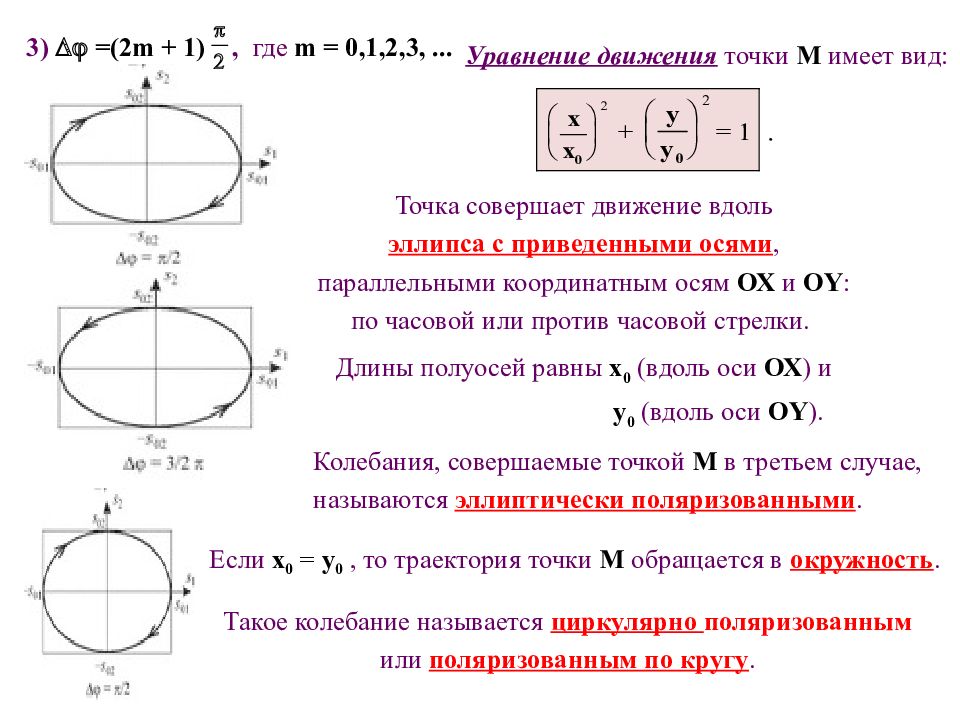
3) =(2 m + 1), где m = 0,1,2,3,... Уравнение движения точки М имеет вид: Точка совершает движение вдоль эллипса с приведенными осями, параллельными координатным осям ОХ и О Y : по часовой или против часовой стрелки. Длины полуосей равны х 0 (вдоль оси ОХ ) и y 0 (вдоль оси О Y ). Такое колебание называется циркулярно поляризованным или поляризованным по кругу. Если х 0 = y 0, то траектория точки М обращается в окружность. Колебания, совершаемые точкой М в третьем случае, называются эллиптически поляризованными.
Слайд 19
Если частоты складываемых взаимно перпендикулярных колебаний некоторой точки М различны, то результирующее движение будет представлять собой сложную кривую линию. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Форма кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. где p и q - целые числа. Фигуры Лиссажу вписываются в прямоугольник с центром в начале координат и длиной сторон 2х 0 вдоль оси ОХ и 2 y 0 вдоль оси О Y. Отношение числа касаний к х и к y фигуры Лиссажу с соответствующими сторонами прямоугольника обратно пропорционально отношению соответствующих частот : Наиболее простой вид имеют фигуры Лиссажу для колебаний с кратными частотами :
Слайд 20
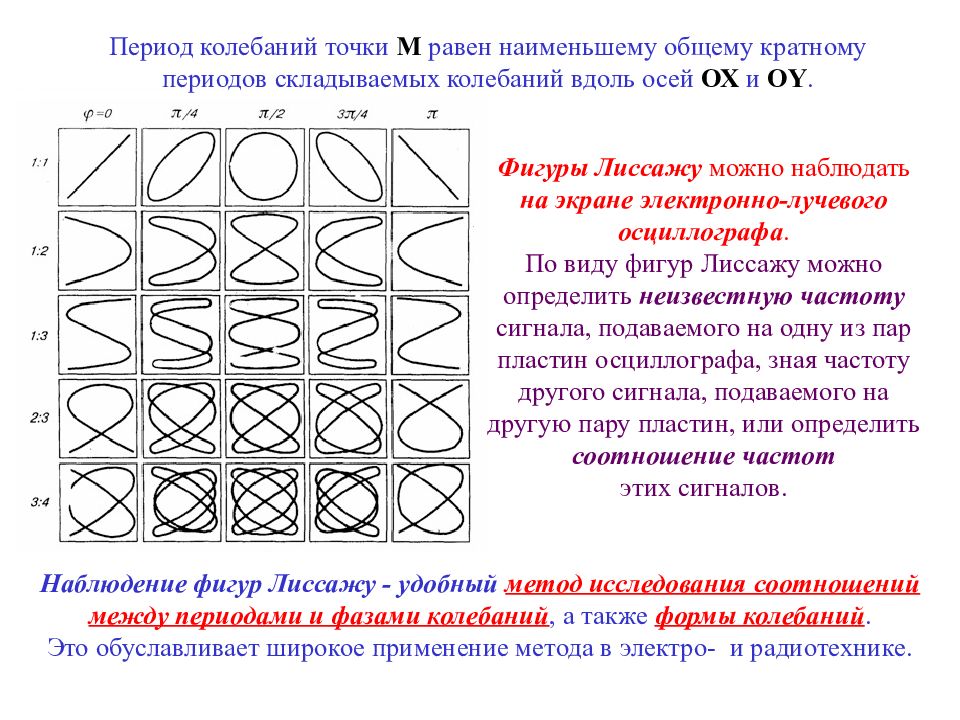
Фигуры Лиссажу можно наблюдать на экране электронно-лучевого осциллографа. По виду фигур Лиссажу можно определить неизвестную частоту сигнала, подаваемого на одну из пар пластин осциллографа, зная частоту другого сигнала, подаваемого на другую пару пластин, или определить соотношение частот этих сигналов. Наблюдение фигур Лиссажу - удобный метод исследования соотношений между периодами и фазами колебаний, а также формы колебаний. Это обуславливает широкое применение метода в электро- и радиотехнике. Период колебаний точки М равен наименьшему общему кратному периодов складываемых колебаний вдоль осей ОХ и О Y.
Слайд 21
5.1.6. Дифференциальное уравнение гармонических колебаний. Линейные и нелинейные колебательные системы. Всякое устройство, способное совершать гармонические колебания, называется гармоническим осциллятором. Если колебание описывается уравнением: то выполняется следующее равенство: из которого следует, что гармонически изменяющаяся величина S удовлетворяет дифференциальному уравнению : (1) (2) Уравнение (1) является общим решением дифференциального уравнения (2), а S 0 и 0 - произвольные постоянные величины, значения которых определяются начальными условиями (т.е. при t = 0 ). Уравнение (1) является кинематическим, а уравнение (2) - динамическим дифференциальным уравнением гармонических колебаний.
Слайд 22
Уравнение (2) является линейным дифференциальным уравнением (функция S ( t ) и её вторая производная входит в уравнение в первой степени). Физические системы, совершающие колебания, с достаточным приближением описываемые линейными дифференциальными уравнениями, называются линейными колебательными системами, все другие - нелинейными. Все реально существующие колебательные системы являются нелинейными. Их свойства зависят от происходящих в них процессов. Примеры нелинейных колебательных систем : 1) Механические системы тел, модули упругости которых зависят от деформации. 2) Электромагнитные системы, содержащие сегнетоэлектрики или ферромагнетики, диэлектрическая и магнитная проницаемости которых зависят от напряжённости электрического или магнитного полей. К нелинейным системам не применяется принцип суперпозиции колебаний. Однако, именно эта особенность нелинейных систем позволяет с их помощью осуществлять генерирование и преобразование частоты электромагнитных колебаний - выпрямление, умножение частоты, модуляцию колебаний.
Слайд 23
5.1.7. Математический и пружинный маятники. Рассмотрим несколько примеров гармонических осцилляторов. 1) Математический маятник. Математический маятник - это идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити длиною l, и колеблющаяся под действием силы тяжести. Материальная точка А отклоняется от положения равновесия на угол против часовой стрелки, а затем отпускается. Сила тяжести создаёт вращательный момент М, где I = m 2 - момент инерции материальной точки; - угловое ускорение. стремящийся вернуть точку в положение равновесия (по часовой стрелке). Сила натяжения нити не создаёт вращательный момент, так как её направление проходит через точку подвеса. Основное уравнение вращательного движения имеет вид: (если угол невелик, то sin ). Т.о. уравнение движения маятника принимает вид:
Слайд 24
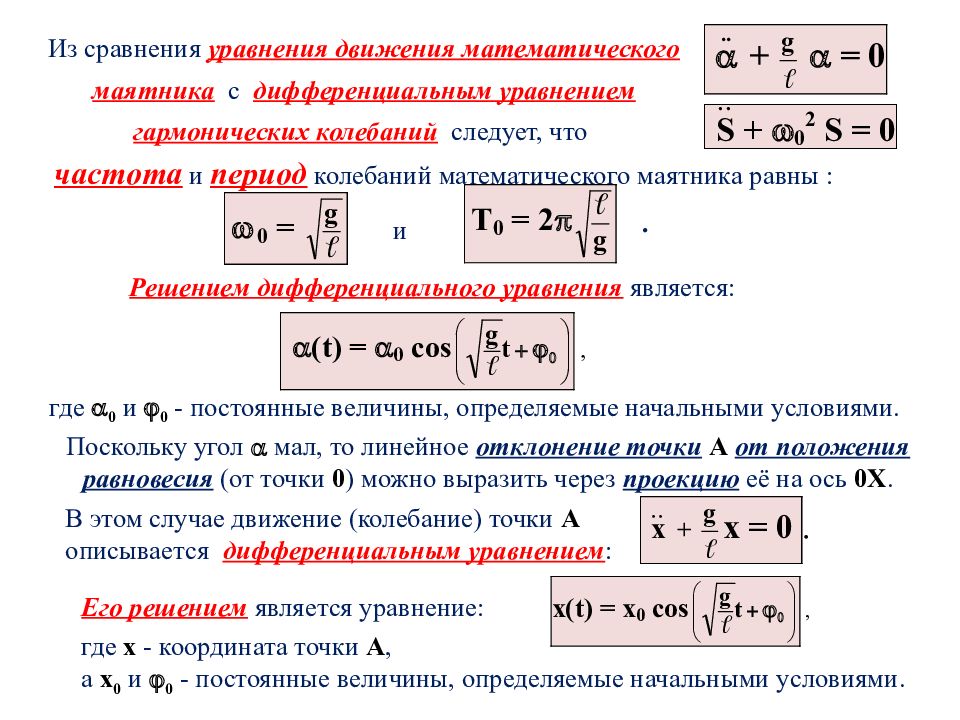
Из сравнения уравнения движения математического маятника с дифференциальным уравнением гармонических колебаний следует, что и . частота и период колебаний математического маятника равны : Решением дифференциального уравнения является: где 0 и 0 - постоянные величины, определяемые начальными условиями. Поскольку угол мал, то линейное отклонение точки А от положения равновесия (от точки 0 ) можно выразить через проекцию её на ось 0Х. Его решением является уравнение: В этом случае движение (колебание) точки А описывается дифференциальным уравнением : где х - координата точки А, а х 0 и 0 - постоянные величины, определяемые начальными условиями.
Слайд 25
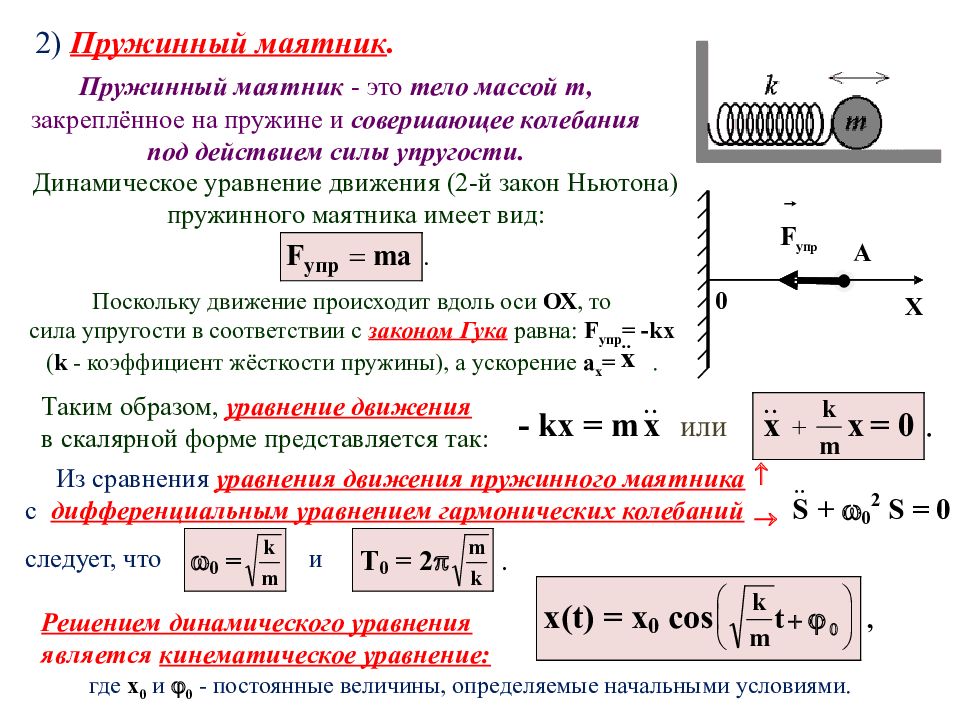
2) Пружинный маятник. Пружинный маятник - это тело массой m, закреплённое на пружине и совершающее колебания под действием силы упругости. Динамическое уравнение движения (2-й закон Ньютона) пружинного маятника имеет вид: Поскольку движение происходит вдоль оси ОХ, то сила упругости в соответствии с законом Гука равна: F упр = - k х ( k - коэффициент жёсткости пружины), а ускорение а х =. Таким образом, уравнение движения в скалярной форме представляется так: Из сравнения уравнения движения пружинного маятника с дифференциальным уравнением гармонических колебаний следует, что и Решением динамического уравнения является кинематическое уравнение: где х 0 и 0 - постоянные величины, определяемые начальными условиями.
Слайд 26
5.1.8. Томсоновский колебательный контур. Формула Томсона. Свободные электрические колебания возникают в простом колебательном контуре, состоящем из конденсатора с электроёмкостью С, соединённой с ним последовательно катушкой индуктивности L и электросопротивлением R =0. Такой колебательный контур называется идеальным. Конденсатор заряжается путём сообщения его обкладкам электрического заряда + q и - q. При этом между обкладками возникает напряжение U = q / C. В результате перетекания зарядов с одной обкладки на другую в контуре возникает электрический ток, сила которого равна. Нарастающий электрический ток возбуждает в контуре ЭДС самоиндукции:. Согласно второму правилу Кирхгофа си = U или. Это уравнение является дифференциальным уравнением идеального колебательного контура. В стандартной форме оно имеет вид: Сравнение его с дифференциальным уравнением гармонических колебаний позволяет выразить частоту и период колебаний идеального контура: Формула, определяющая период колебаний называется формулой Томсона. , Решением дифференциального уравнения является : где q 0 и 0 - постоянные величины, определяемые начальными условиями.
Слайд 27
5.1.9. Энергетические соотношения для осцилляторов. а) Механические колебания. При свободных гармонических колебаниях в механической системе происходит периодическое преобразование кинетической энергии системы в потенциальную (например, в математическом маятнике - это потенциальная энергия материальной точки поднятой на некоторую высоту относительно равновесного положения, а в пружинном маятнике - потенциальная энергия упругой деформации пружины). Очевидно, что полная механическая энергия колебательной системы в процессе колебаний не меняется. На рисунке представлены временные зависимости кинетической и потенциальной энергии механического осциллятора.
Слайд 28
б) Электромагнитные колебани я При свободных гармонических колебаниях в идеальном колебательном контуре происходит периодическое преобразование энергии электрического поля W э конденсатора в энергию магнитного поля W м катушки индуктивности и наоборот: Колебания, происходящие в электрическом колебательном контуре, называются электромагнитными. Колебания электрической и магнитной ( W э и W м ) составляющих происходят в противофазе, то есть, в те моменты, когда энергия электрического поля обращается в нуль, энергия магнитного поля становится максимальной, и наоборот. Полная же энергия электромагнитных колебаний в контуре с течением времени не изменяется : График зависимостей W э ( t ) и W м ( t ) выглядит аналогично графику зависимостей W п ( t ) и W к ( t ) соответственно.
Слайд 29
5.2. ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. 5.2.1. Свободные затухающие (механические и электромагнитные) колебания и их дифференциальное уравнение. Логарифмический декремент затухания, добротность, время релаксации. Свободные колебания в реальных системах всегда с течением времени затухают. Затухание колебаний обусловлено потерей энергии системой с течением времени. Затухание механических колебаний обусловлено трением, сопротивлением окружающей среды и возбуждением в ней упругих волн. Затухание электромагнитных колебаний контура обусловлено тепловыми потерями в проводниках, потерями на излучение электромагнитных волн. В нелинейных колебательных системах - тепловыми потерями в диэлектриках и ферромагнетиках вследствие электрического или магнитного гистерезиса. Получим дифференциальное уравнение затухающих колебаний линейных систем. 1. Механическая система - пружинный маятник. Материальная точка массой m, прикреплённая к пружине с жёсткостью k, совершает колебания в вязкой среде вдоль оси ОХ. На такой пружинный маятник действуют две силы: 1) сила упругости F упр = - k х (в соответствии с законом Гука ); 2) сила сопротивления вязкой среды, пропорциональная скорости v движения и направленная против движения ( r - коэффициент вязкости среды).
Слайд 30
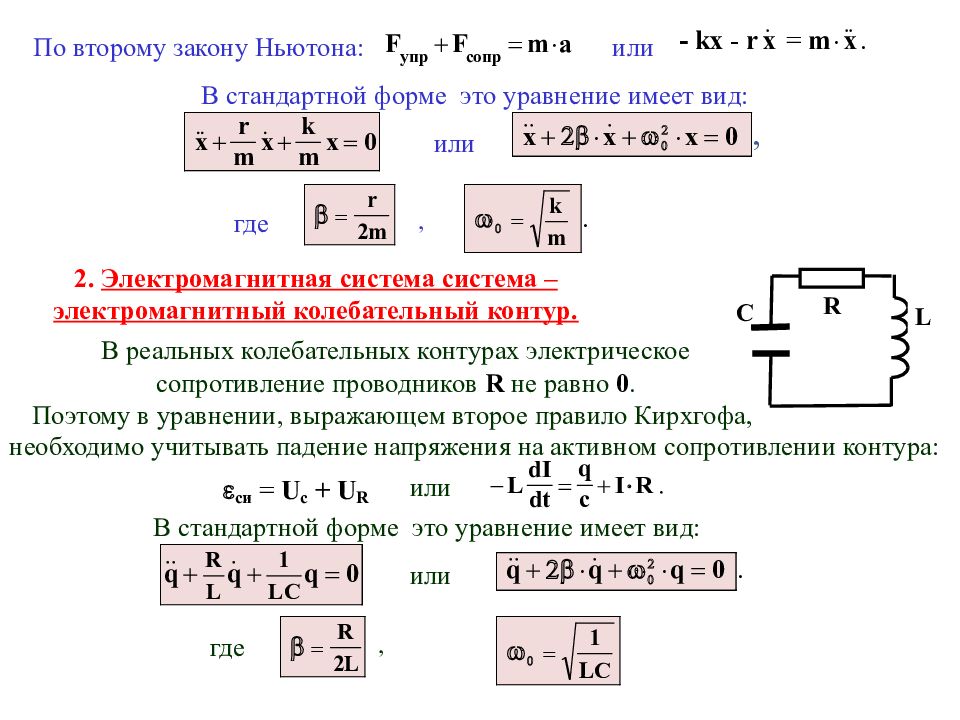
По второму закону Ньютона: или В стандартной форме это уравнение имеет вид: или где , 2. Электромагнитная система система – электромагнитный колебательный контур. В реальных колебательных контурах электрическое сопротивление проводников R не равно 0. Поэтому в уравнении, выражающем второе правило Кирхгофа, необходимо учитывать падение напряжения на активном сопротивлении контура: или В стандартной форме это уравнение имеет вид: или где , .
Слайд 31
Уравнения и можно представить в обобщённой форме: Это уравнение является дифференциальным уравнением свободных затухающих колебаний линейных систем, где S - изменяющаяся при колебаниях физическая характеристика системы, - коэффициент затухания колебательной системы, 0 - циклическая частота свободных незатухающих колебаний той же системы в отсутствие потерь ( = 0 ). Это линейное, однородное дифференциальное уравнение имеет следующее решение : в котором величина называется условной частотой затухающих колебаний. а постоянные величины S 0 и 0 находятся из начальных условий, то есть по значениям:
Слайд 32
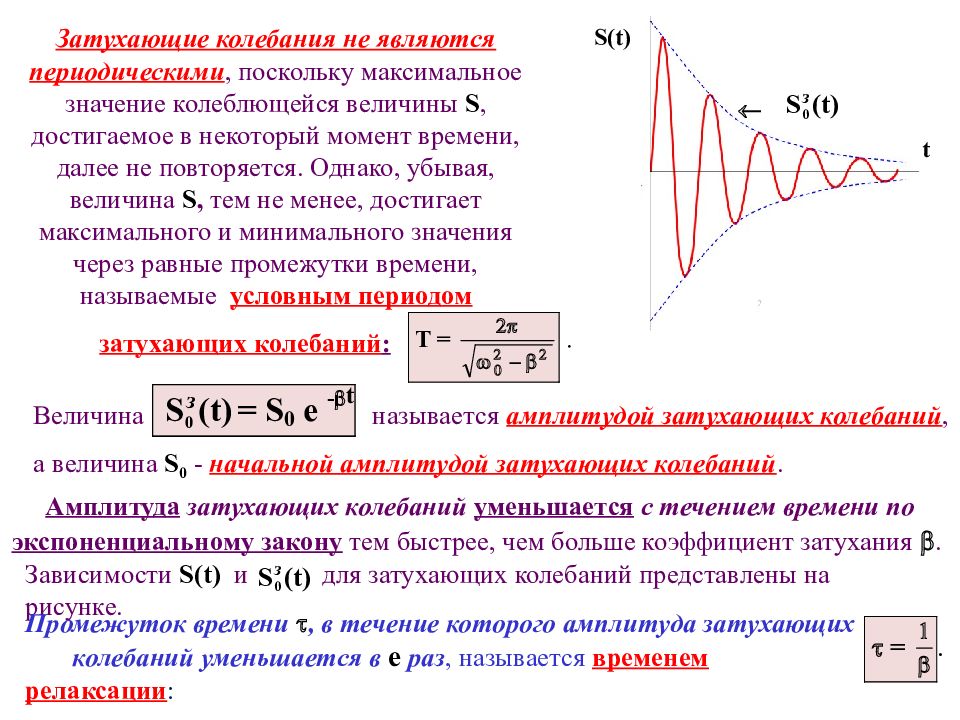
Затухающие колебания не являются периодическими, поскольку максимальное значение колеблющейся величины S, достигаемое в некоторый момент времени, далее не повторяется. Однако, убывая, величина S, тем не менее, достигает максимального и минимального значения через равные промежутки времени, называемые условным периодом затухающих колебаний : а величина S 0 - начальной амплитудой затухающих колебаний. Величина называется амплитудой затухающих колебаний, Амплитуда затухающих колебаний уменьшается с течением времени по экспоненциальному закону тем быстрее, чем больше коэффициент затухания . S ( t ) t Зависимости S ( t ) и для затухающих колебаний представлены на рисунке. Промежуток времени , в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации :
Слайд 33
Для количественной характеристики быстроты убывания амплитуды затухающих колебаний вводится декремент затухания, определяющий, во сколько раз уменьшается амплитуда затухающих колебаний за время, равное одному периоду: Часто для характеристики затухающих колебаний более удобно использовать не декремент, а логарифм декремента затухания. Эта величина называется логарифмическим декрементом затухания : где N - число колебаний, в течение которых амплитуда уменьшается в е раз. Для характеристики быстроты убывания энергии колебательной системы за один условный период затухающих колебаний вводится добротность Q : (здесь использовано приближение - при <<1 e -2 T 1 - 2 T ). Для пружинного маятника : для электромагнитного колебательного контура : (здесь - волновое сопротивление колебательного контура).
Слайд 34
5.2.2. Вынужденные механические колебания осциллятора под воздействием синусоидальной силы. Процесс установления колебаний. Время установления колебаний и его связь с добротностью. Амплитуда и фаза при вынужденных колебаниях. Резонанс. Под действием переменной внешней силы механическая система совершает вынужденные колебания. Получим дифференциальное уравнение вынужденных колебаний простейшей линейной колебательной системы – пружинного маятника, происходящих вдоль оси ОХ под действием вынуждающей силы, изменяющейся по гармоническому закону: F x ( t ) = F 0 cos ( t ), где F 0 - амплитуда вынуждающей силы, - частота вынуждающей силы. Вынужденные колебания пружинного маятника совершаются под действием трёх сил: силы упругости, силы сопротивления среды и вынуждающей силы. Их динамическое уравнение имеет вид: F упр + F сопр + F x = ma или
Слайд 35
Это уравнение является линейным, неоднородным дифференциальным уравнением второго порядка. Его решением является сумма общего решения х 1 ( t ) однородного уравнения (аналогичного уравнению затухающих колебаний) и частного решения х 2 ( t ) неоднородного уравнения (уравнения вынужденных колебаний): В стандартной форме уравнение вынужденных колебаний имеет вид: Первое решение х 1 ( t ) играет роль только в процессе установления вынужденных колебаний. Его амплитудное значение, равное х 0. е - t, более или менее быстро уменьшается. За время 0 = ln100/β амплитуда затухающих колебаний уменьшается в 100 раз.
Слайд 36
За время 0 свободные колебания маятника практически прекращаются, и маятник переходит в состояние установившихся вынужденных колебаний, совершающихся с частотой вынуждающей силы, амплитудой А и начальной фазой 0В. При этом: х( t ) х 2 ( t ). Время 0 называется временем установления вынужденных колебаний. Время 0 прямо пропорционально добротности Q колебательной системы: Q = π/( βT ), β ~ 1/Q и 0 ~ Q. Значения амплитуды А и начальной фазы 0В вынужденных колебаний зависят от соотношения между частотой вынуждающей силы и частотой 0 собственных (свободных незатухающих) колебаний, а также от коэффициента затухания : При = 0 0В = 0 и То есть, под действием постоянной силы F x = F 0 происходит статическое смещение маятника от положения равновесия. При 0В и А( ) 0.
Слайд 37
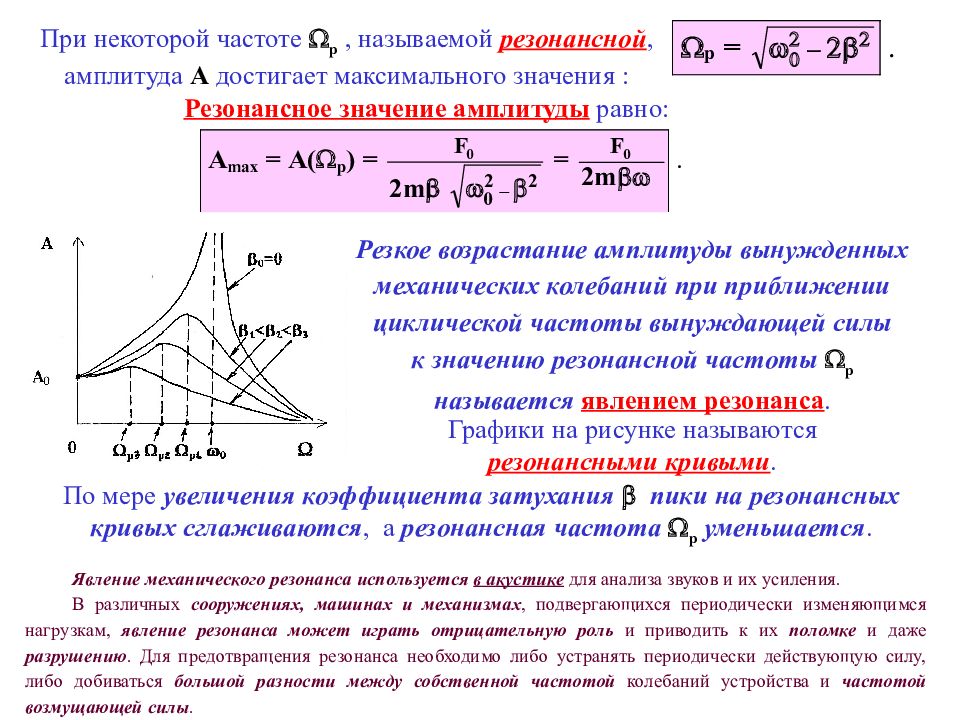
При некоторой частоте р, называемой резонансной, амплитуда А достигает максимального значения : Резонансное значение амплитуды равно: Резкое возрастание амплитуды вынужденных механических колебаний при приближении циклической частоты вынуждающей силы к значению резонансной частоты р называется явлением резонанса. По мере увеличения коэффициента затухания пики на резонансных кривых сглаживаются, а резонансная частота р уменьшается. Графики на рисунке называются резонансными кривыми. Явление механического резонанса используется в акустике для анализа звуков и их усиления. В различных сооружениях, машинах и механизмах, подвергающихся периодически изменяющимся нагрузкам, явление резонанса может играть отрицательную роль и приводить к их поломке и даже разрушению. Для предотвращения резонанса необходимо либо устранять периодически действующую силу, либо добиваться большой разности между собственной частотой колебаний устройства и частотой возмущающей силы.
Слайд 38
5.2.3. Вынужденные колебания в электрических цепях. Для осуществления вынужденных колебаний в электромагнитном колебательном контуре в него нужно включить источник энергии, ЭДС которого изменяется по периодическому закону. где 0 – амплитудное значение ЭДС, - частота переменной ЭДС. Второе правило Кирхгофа в этом случае имеет вид: В стандартной форме уравнение вынужденных колебаний имеет вид: Это уравнение является дифференциальным уравнением вынужденных электромагнитных колебаний контура (по структуре оно полностью соответствует уравнению для механических колебаний). Решение уравнения, как и в случае механических колебаний, является суммой общего решения однородного уравнения q 1 (t) и частного решения неоднородного уравнения q 2 (t). В наиболее простом случае ЭДС изменяется по гармоническому закону : ~ ( t)
Слайд 39
При установившихся колебаниях (т.е. при t >> t 0 ) q(t) q 2 (t). Амплитуда q 0 и начальная фаза 0В вынужденных электромагнитных колебаний находятся по формулам, полученным для механических колебаний: Если учесть, что то эти формулы приобретают вид: Сила тока при установившихся вынужденных колебаниях в контуре равна: I = = - q 0 sin( t + 0 В ) = q 0 cos( t + 0 В + /2) = I 0 cos( t - ), где I 0 = q 0 - амплитудное значение силы тока, = - ( 0В + /2) – сдвиг фаз между током и напряжением в контуре.
Слайд 40
Таким образом, амплитудное значение силы тока в контуре и сдвиг фаз между током и напряжением определяются формулами: Графики зависимостей I 0 ( ) и ( ) представлены на рисунке. Зависимости I 0 ( ) при разных R называются резонансными кривыми колебательного контура. Максимальный ток в контуре возникает в случае, когда L - 1/ C = 0 или при частоте внешнего напряжения, равной: Эта частота называется резонансной. Рассмотренное явление называется резонансом напряжений. Амплитуда силы тока при резонансе напряжений равна : I 0 ( р ) = 0 /R, а сдвиг фаз между током и напряжением : ( р ) = 0.
Слайд 41
5.3. ВОЛНОВЫЕ ПРОЦЕССЫ 5.3.1. Механизм образования механических волн. Продольные и поперечные волны. Упругие волны в твёрдых телах, газах и жидкостях. Волны - это изменения состояния среды (возмущения), распространяющиеся в среде или вакууме и несущие с собой энергию. Основное свойство волн, не зависящее от их природы - это перенос энергии без переноса вещества. В реальных колебательных системах амплитуда колебаний с течением времени уменьшается из-за рассеяния энергии в окружающей среде. Это происходит в результате возбуждения в среде механических или электромагнитных волн. В природе и технике встречается три типа волн: 1) упругие ; 2) электромагнитные ; 3) волны на поверхности жидкости.
Слайд 42
Волны могут иметь различную форму: 1) одиночная волна или импульс ; 2) цуг - ограниченный ряд повторяющихся возмущений; 3) неограниченная волна, в частности гармоническая волна. Волны могут различаться по тому, как возмущение ориентированы относительно направления распространения. В продольной волне возмущения (смещения) происходят в направлении распространения волны. Пример - звук. В поперечной волне возмущения (смещения) перпендикулярны направлению распространения волны. Примеры - колебания струны, электромагнитные волны. Волны на поверхности жидкости возникают под влиянием внешнего воздействия, выводящего жидкость из состояния равновесия. В результате этого возникают силы, восстанавливающие равновесие – силы поверхностного натяжения и гравитации. Молекулы в этом случае совершают движение по эллипсу. Таким образом, эти волны не являются ни продольными, ни поперечными. Это особый вид волн, математическое описание которых достаточно сложное.
Слайд 43
Ниже рассматриваются только механические и электромагнитные волны. Механическими (упругими) волнами называется процесс распространения механических колебаний в упругой среде. Упругая (сплошная) среда - это среда, непрерывно распределённая в пространстве и обладающая упругими свойствами. То есть не учитывается молекулярное строение упругой среды, а внутренние силы, возникающие при её деформациях, пропорциональны этим деформациям ( закон Гука ). В первом приближении все среды (кроме разрежённых газов) можно считать упругими. Механические продольные волны связаны с объёмной деформацией среды - сжатием и растяжением. Они могут возникать как в твёрдых телах, так и жидкостях и газах. Механические поперечные волны связаны с деформацией формы среды - сдвигом. Они могут возникать только в твёрдых телах.
Слайд 44
5.3.2. Уравнения бегущих волн (плоской и сферической). Фазовая скорость, длина волны, волновое число и волновой вектор. Связь фазовой скорости с волновым вектором. Одномерное волновое уравнение. Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. На рисунке представлен график гармонической поперечной волны, распространяющейся со скоростью вдоль оси Х. Источник колебаний находится в начале координат. На графике S ( x, t *) изображена зависимость смещения S частиц среды от их координаты x в некоторый фиксированный момент времени t *. Аналогично может быть представлен график S ( x *, t ) зависимости смещения S любой частицы среды с фиксированной координатой х* от времени t. Расстояние между ближайшими точками, колеблющимися в одинаковой фаза, называется длиной волны . Длина волны равна тому расстоянию, на которое распространяется определённая фаза колебания за один период, то есть: λ = vT = v / ν (здесь - линейная частота колебаний). t * - фиксировано S ( x, t *)
Слайд 45
Скорость, с которой распространяется какая-либо фаза волны, называется фазовой скоростью v. В фиксированный момент времени волновых поверхностей существует бесчисленное множество, а волновой фронт - только один. В зависимости от формы волновых поверхностей волны называют плоскими, сферическими, цилиндрическими и т.д. Если источник колебаний находится в некоторой среде, то с течением времени в колебательный процесс будут вовлекаться всё новые области этой среды. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Распространение механических волн в среде связано с переносом энергии (в отличие от стоячих волн). Поэтому такие волны принято называть бегущими.
Слайд 46
Получим уравнение плоской бегущей волны. Источник колебаний находится в начале координат ( х = 0 ) и совершает колебания по закону: S (0, t ) = S 0 cos ( t + 0 ). Некоторая точка В с координатой х колеблется по такому же закону, но её колебания будут отставать по времени на величину = х/ v, где v - скорость распространения волны. Уравнение колебаний точки В имеет вид: Это и есть уравнение плоской бегущей волны. Если волна распространяется в противоположном оси Х направлении, её называют встречной волной, а её уравнение имеет вид: Для характеристики волн используется волновой вектор, ориентированный вдоль направления распространения волны и равный: Фазовая скорость и волновой вектор связаны друг с другом соотношением:
Слайд 47
Введение волнового числа и волнового вектора позволяет уравнение плоской бегущей волны представить: - в экспоненциальной форме (на основании формул Эйлера ), где физический смысл имеет только действительная часть. - в векторной форме - в скалярной форме Уравнение сферической волны, волновые поверхности которой - концентрические сферы, записывается так: где S 0 ( r ) ~1/ r ; r - расстояние от источника колебаний до рассматриваемой точки сферы ( r значительно превышает размеры источника волны). Амплитуда сферической волны даже в среде, не поглощающей энергию, убывает обратно пропорционально расстоянию от источника волны.
Слайд 48
Вектор фазовой скорости параллелен волновому вектору, а оба эти вектора перпендикулярны волновой поверхности. Фазовая скорость продольной волны в тонком стержне равна: Фазовая скорость поперечной волны в струне равна: где Е - модуль Юнга, - плотность материала стержня ( Е = σ/ε, = F / S - механическое напряжение, = l / l - относительное удлинение стержня ). где G - модуль сдвига, - плотность материала струны ( G = / , = F / S - напряжение сдвига; - деформация сдвига). Скорость распространения гармонической волны является фазовой скоростью. Она равна скорости перемещения волновой поверхности (то есть точек, имеющих определённое значение фазы: = const ). В случае плоской гармонической волны из условия ( t, x ) = t - kx + 0 = const следует:
Слайд 49
Получим динамическое дифференциальное уравнение плоской гармонической волны, распространяющейся вдоль оси Х со скоростью v. называемое волновым уравнением. Кинематическое уравнение такой волны: S(x,t) = S 0 cos ( t - kx + 0 ). Вторые производные функции S ( x, t ) по параметрам х и t равны: Отсюда следует волновое уравнение плоской гармонической волны : Кинематическое уравнение плоской гармонической волны является решением этого дифференциального уравнения. где - оператор Лапласа, равный: В общем случае распространение волн в однородной изотропной среде описывается волновым уравнением : Решениями дифференциальных уравнений являются кинематические уравнения плоских или сферических волн.
Слайд 50
5.3.3. Энергия волн. Поток энергии. Вектор Умова. Упругая среда, в которой распространяется механическая волна, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной её деформацией. Рассмотрим плоскую продольную гармоническую волну, уравнение которой имеет вид: S ( x, t ) = S 0 cos ( t - kx + 0 ). Выделим в среде малый объём V такой, что для всех его частиц производные ( S/ t ) и ( S/ x ) были одинаковыми. Кинетическая энергия частиц этого объёма равна: Потенциальная энергия равна: Полная энергия равна:
Слайд 51
Объёмная плотность энергии равна: Среднее значение объёмной плотности энергии равно: C реда, в которой распространяется волна, обладает дополнительным запасом энергии. Волна переносит эту энергию от источника к различным точкам среды. Потоком энергии называется энергия, переносимая через некоторую поверхность за единицу времени: P = dW/dt. Интенсивность потока характеризуется плотностью потока энергии – векторной величиной, направленной в сторону переноса энергии, численно равной потоку энергии через единичную площадку, перпендикулярную этому направлению. По модулю плотность потока энергии равна: А в векторной форме : Этот вектор называется вектором Умова. Если плотность потока энергии в среде постоянна, то Р = J. S . Если же она в разных точках различна, то
Слайд 52
5.3.4. Принцип суперпозиции волн и границы его применимости. Когерентность. Интерференция синусоидальных волн. Связь между разностью хода и разностью фаз. В линейных средах, свойства которых не изменяются при распространении в них волн, волновые процессы подчиняются принципу суперпозиции - При сложении в пространстве когерентных волн наблюдается явление интерференции - усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Особый интерес представляет суперпозиция когерентных волн. Обычно амплитуда, частота и фаза волн, излучаемых реальными источниками, изменяется беспорядочно. Когерентными могут быть только волны, имеющие одинаковую частоту. К когерентным волнам применимы известные законы сложения колебаний. Если при этом разность фаз двух или нескольких волн остаётся постоянной во времени, то волны называются когерентными. результирующее возмущение в какой-либо точке линейной среды при одновременном распространении в ней нескольких волн равно сумме возмущений, соответствующих каждой из этих волн.
Слайд 53
Рассмотрим сложение двух когерентных волн, распространяющихся от точечных источников S 1 и S 2 в направлениях и соответственно. Уравнения этих волн : S 1 (r, t) = S 0 1 cos ( t - kr 1 + 0 1 ), S 2 ( r, t) = S 0 2 cos ( t - kr 2 + 0 2 ), где k = 2π/λ = const. Результирующая волна описывается уравнением: в котором амплитуда определяется формулой: где = k r (при 01 = 02 ). Величина r называется геометрической разностью хода волн. Формула устанавливает связь между разностью фаз и разностью хода волн.
Слайд 54
Поскольку энергия, переносимая волной, пропорциональна квадрату амплитуды, то в точках, в которых выполняется условие: наблюдается усиление интенсивности результирующей волны. Эти точки соответствуют интерференционным максимумам. В точках, в которых выполняется условие: наблюдается ослабление интенсивности результирующей волны. Эти точки соответствуют интерференционным минимумам. Число m называется порядком интерференционного максимума или минимума.
Слайд 55
5.3.5. Стоячие волны, узлы и пучности. Частным случаем интерференции волн являются стоячие волны, которые образуются при наложении двух встречных бегущих волн с одинаковой амплитудой и частотой. Например, две плоских волны, описывающиеся уравнениями: S 1 ( х, t) = S 0 cos ( t - k х ), S 2 ( х, t) = S 0 cos ( t + k х ) (начало координат выбрано в точке, в которой волны имеют одинаковую фазу, а отсчёт времени начинается с момента, когда фазы обеих волн равны нулю). Уравнение результирующей стоячей волны : S( х,t) = S 1 ( х,t) + S 2 ( х,t) = 2S 0 cosk х cos t. Результирующие колебания происходят с той же частотой , что и исходные, а их амплитуда зависит от координаты точк и и определяется уравнением: S 0 ст (х) = |2 S 0 cosk х|. Точки, в которых амплитуда максимальна и равна 2 S 0, называются пучностями стоячей волны. Точки, в которых амплитуда равна нулю, называются узлами стоячей волны.
Слайд 56
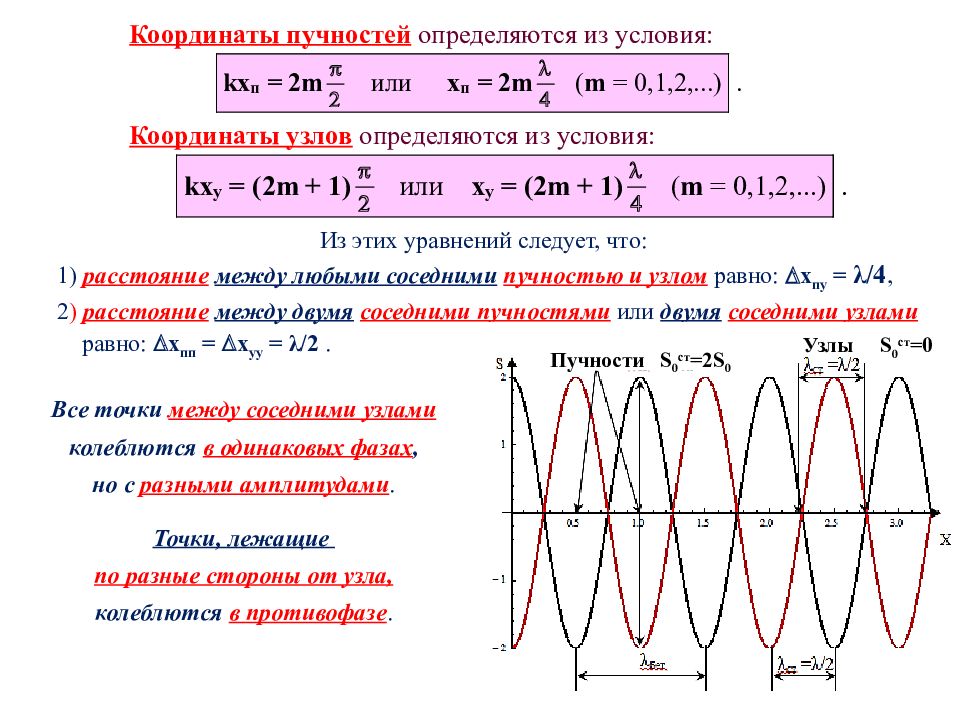
Координаты пучностей определяются из условия: Координаты узлов определяются из условия: Все точки между соседними узлами колеблются в одинаковых фазах, но с разными амплитудами. Точки, лежащие по разные стороны от узла, колеблются в противофазе. Из этих уравнений следует, что: 1) расстояние между любыми соседними пучностью и узлом равно: х пу = λ/4, 2 ) расстояние между двумя соседними пучностями или двумя соседними узлами равно: х пп = х уу = λ/2. Узлы S 0 ст = 0 Пучности S 0 ст =2 S 0
Слайд 57
Стоячие волны образуются при наложении бегущей и отражённой волн. При отражении от более плотной среды волна меняет фазу на противоположную. Поэтому на границе раздела сред образуется узел. При отражении от менее плотной среды волна не меняет фазу. Поэтому на границе образуется пучность. Бегущая и отражённая волны несут одинаковую энергию в противоположные стороны, поэтому полная энергия результирующей стоячей волны, заключённая между узлами, остаётся постоянной. Таким образом, стоячая волна не переносит энергию в пространстве. Отсюда возникло название - стоячая волна. Только в пределах расстояния, равного половине длины волны, происходит взаимное превращение кинетической энергии движения частиц в потенциальную энергию их взаимодействия (энергию деформации) и обратно.
Слайд 58
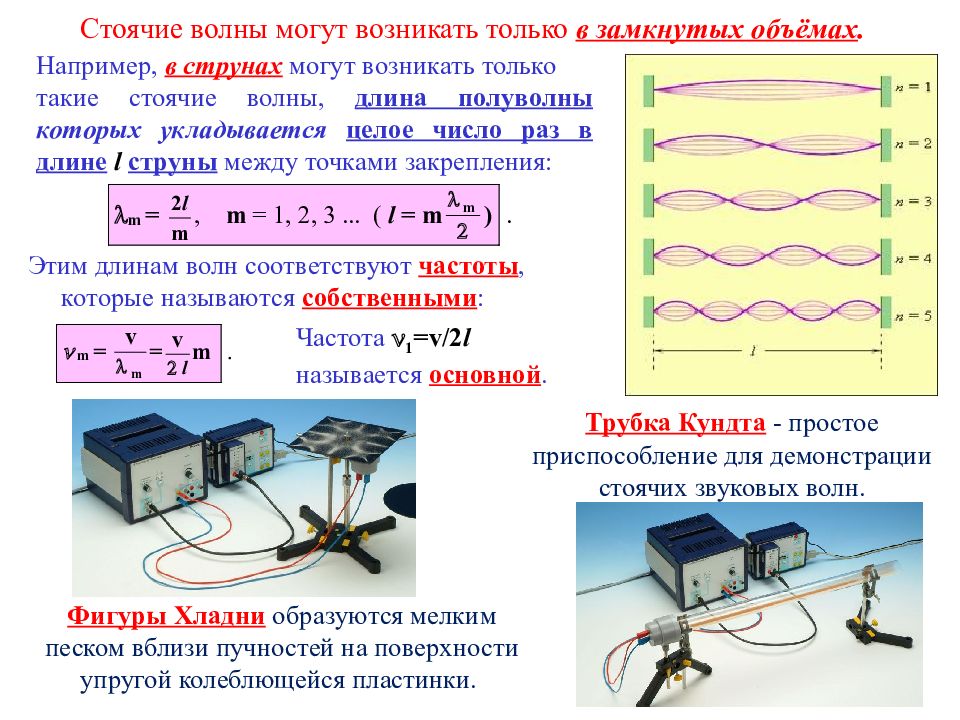
Стоячие волны могут возникать только в замкнутых объёмах. Этим длинам волн соответствуют частоты, которые называются собственными : Частота 1 = v/2 l называется основной. Например, в струнах могут возникать только такие стоячие волны, длина полуволны которых укладывается целое число раз в длине l струны между точками закрепления: Фигуры Хладни образуются мелким песком вблизи пучностей на поверхности упругой колеблющейся пластинки. Трубка Кундта - простое приспособление для демонстрации стоячих звуковых волн.
Слайд 59
5.3.6. Распространение волн в средах с дисперсией. Групповая скорость и её связь с фазовой скоростью. Нормальная и аномальная дисперсия. В пределах пакета волны в большей или меньшей степени усиливают друг друга, вне пакета - практически полностью гасят друг друга. Понятие фазовой скорости имеет смысл только для монохроматических волн. Реально существуют ограниченные цуги волн. Любую ограниченную волну можно представить, как наложение большого числа монохроматических волн с различной частотой. Суперпозиция волн с мало отличающимися частотами, занимающими в каждый момент времени ограниченную область пространства, называется группой волн или волновым пакетом. Если дисперсии нет, то волновой пакет распространяется со скоростью, равной фазовой. В диспергированных средах волновой пакет со временем расплывается. Скорость распространения волн может зависеть от частоты (длины волны). В этом случае наблюдается дисперсия волн.
Слайд 60
Если дисперсия невелика, то расплывание пакета происходит медленно, и ему можно приписать некоторую скорость u, называемую групповой, которая характеризует скорость перемещения центра волнового пакета : В диспергированной среде групповая скорость отличается от фазовой. В зависимости от знака производной групповая скорость может быть больше или меньше фазовой: Групповая скорость всегда меньше скорости света в вакууме u < с. Для фазовой скорости таких ограничений не существует. Обычно понятие групповой скорости вводится для сред с малым поглощением энергии. если дисперсия называется нормальной и u < v, если дисперсия называется аномальной и u > v, если дисперсии нет и u = v.
Слайд 61
5.3.7. Электромагнитные волны. Предсказание электромагнитных волн теорией Максвелла. Волновое уравнение для электромагнитной волны. Скорость распространения электромагнитных волн в средах. Закон Максвелла. Дифференциальное уравнение плоской монохроматической электромагнитной волны. Поляризация волн. Электромагнитные волны - это возмущения электромагнитного поля, распространяющиеся в пространстве. Существование электромагнитных волн вытекает из уравнений Максвелла. Из уравнений Максвелла следует, что в однородной изотропной среде вдали от электрических зарядов и токов, создающих электромагнитное поле, векторы напряжённости электрического и магнитного полей удовлетворяют волновым уравнениям : Решающую роль в утверждении теории Максвелла явились опыты Герца (1888 год), доказавшие, что электромагнитное поле, действительно, распространяется в виде волн. Здесь - лапласиан, v - фазовая скорость, определяемая законом Максвелла : совпадает со скоростью света в вакууме. В вакууме v = c, а в любой среде r r > 1 и v < c.
Слайд 62
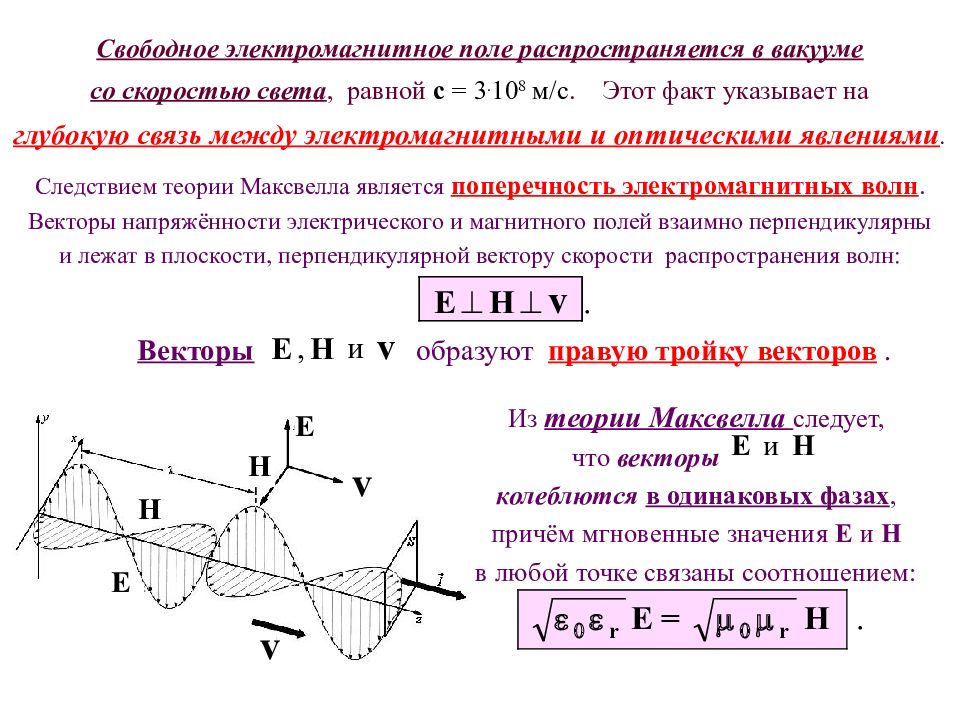
Свободное электромагнитное поле распространяется в вакууме со скоростью света, равной c = 3. 10 8 м/с. Этот факт указывает на глубокую связь между электромагнитными и оптическими явлениями. Следствием теории Максвелла является поперечность электромагнитных волн. Векторы напряжённости электрического и магнитного полей взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору скорости распространения волн: Из теории Максвелла следует, что векторы колеблются в одинаковых фазах, причём мгновенные значения Е и Н в любой точке связаны соотношением: Векторы образуют правую тройку векторов.
Слайд 63
Поскольку векторы образуют правую тройку векторов, то волновые уравнения можно записать в скалярной форме следующим образом: (другие компоненты векторов равны нулю). Этим уравнениям, в частности, удовлетворяет плоская монохроматическая электромагнитная волна, описываемая уравнениями: Е y = E 0 cos ( t -kx + 0 ), H z = H 0 cos ( t -kx + 0 ) (фазы колебаний одинаковы). Если векторы в электромагнитной волне колеблются каждый в определённой плоскости, то волна называется линейно поляризованной. Плоскость, в которой колеблется вектор, называется плоскостью поляризации. Если концы векторов описывают эллипсы в плоскости, перпендикулярной вектору, то волна называется эллиптически поляризованной, если окружности - то циркулярно поляризованной.
Слайд 64
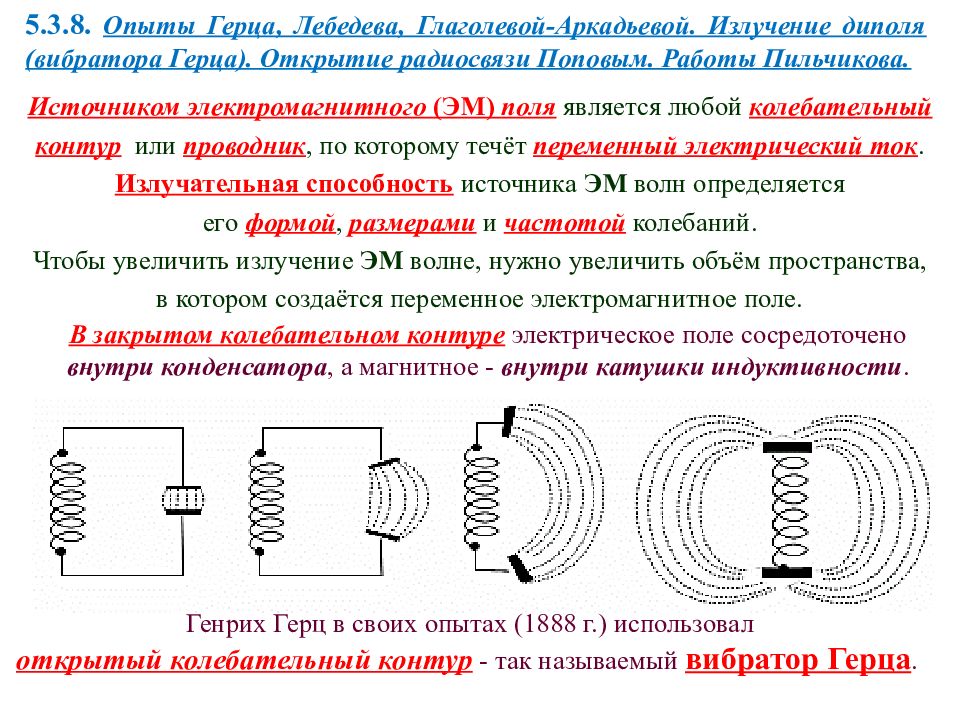
5.3.8. Опыты Герца, Лебедева, Глаголевой-Аркадьевой. Излучение диполя (вибратора Герца). Открытие радиосвязи Поповым. Работы Пильчикова. Источником электромагнитного (ЭМ) поля является любой колебательный контур или проводник, по которому течёт переменный электрический ток. Излучательная способность источника ЭМ волн определяется его формой, размерами и частотой колебаний. Чтобы увеличить излучение ЭМ волне, нужно увеличить объём пространства, в котором создаётся переменное электромагнитное поле. В закрытом колебательном контуре электрическое поле сосредоточено внутри конденсатора, а магнитное - внутри катушки индуктивности. Генрих Герц в своих опытах (1888 г.) использовал открытый колебательный контур - так называемый вибратор Герца.
Слайд 65
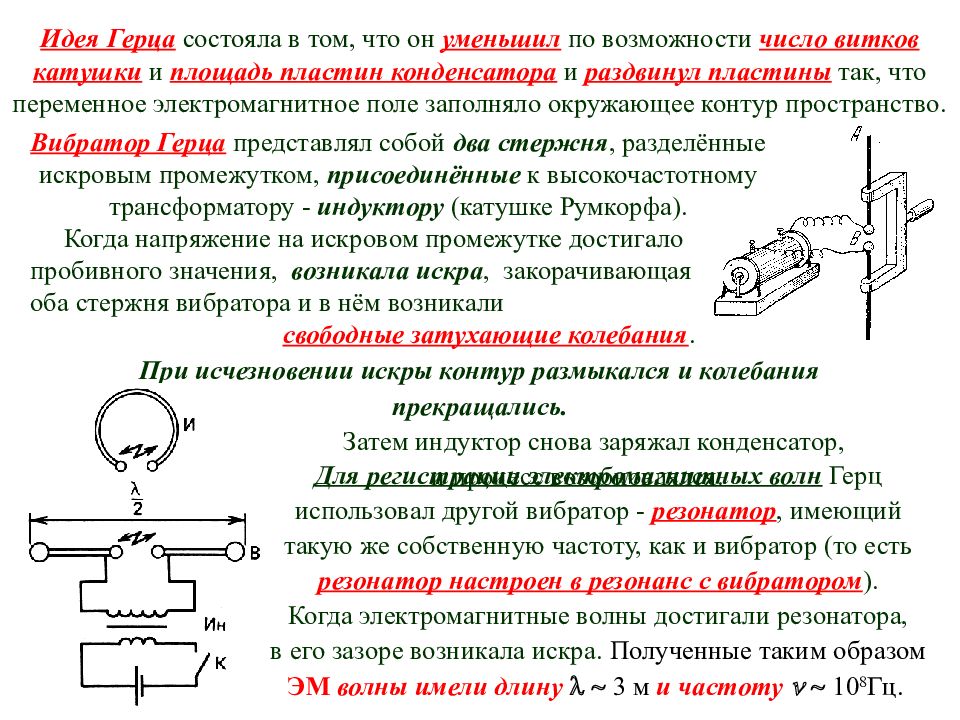
Вибратор Герца представлял собой два стержня, разделённые искровым промежутком, присоединённые к высокочастотному трансформатору - индуктору (катушке Румкорфа). Когда напряжение на искровом промежутке достигало пробивного значения, возникала искра, закорачивающая оба стержня вибратора и в нём возникали свободные затухающие колебания. Идея Герца состояла в том, что он уменьшил по возможности число витков катушки и площадь пластин конденсатора и раздвинул пластины так, что переменное электромагнитное поле заполняло окружающее контур пространство. Для регистрации электромагнитных волн Герц использовал другой вибратор - резонатор, имеющий такую же собственную частоту, как и вибратор (то есть резонатор настроен в резонанс с вибратором ). Когда электромагнитные волны достигали резонатора, в его зазоре возникала искра. Полученные таким образом ЭМ волны имели длину 3 м и частоту 10 8 Гц. При исчезновении искры контур размыкался и колебания прекращались. Затем индуктор снова заряжал конденсатор, и процесс возобновлялся.
Слайд 66
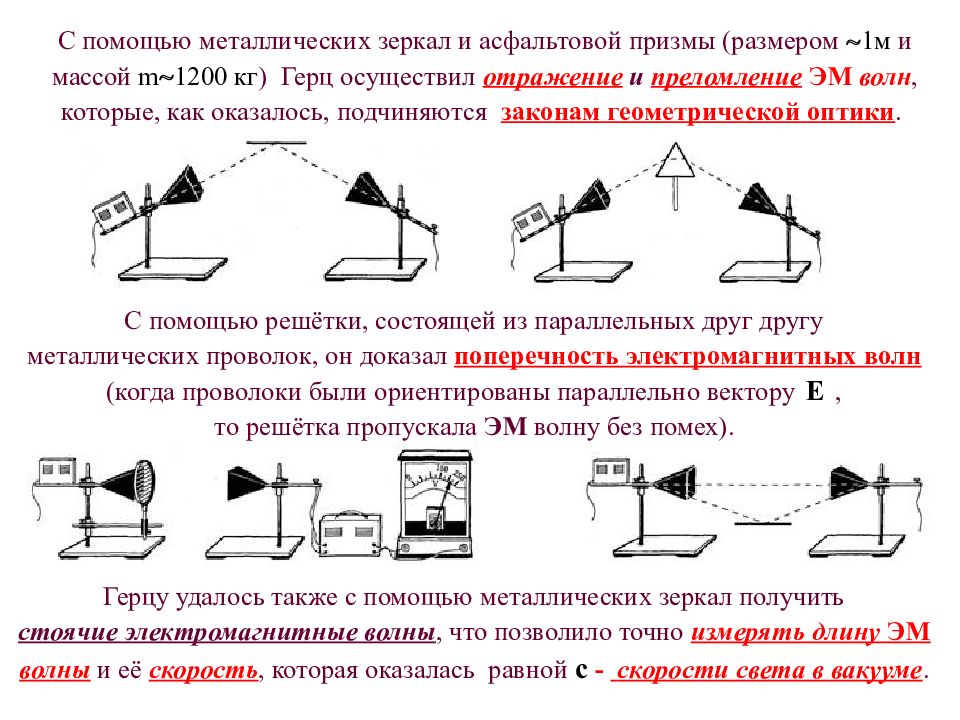
С помощью металлических зеркал и асфальтовой призмы (размером 1м и массой m 1200 кг ) Герц осуществил отражение и преломление ЭМ волн, которые, как оказалось, подчиняются законам геометрической оптики. Герцу удалось также с помощью металлических зеркал получить стоячие электромагнитные волны, что позволило точно измерять длину ЭМ волны и её скорость, которая оказалась равной с - скорости света в вакууме. С помощью решётки, состоящей из параллельных друг другу металлических проволок, он доказал поперечность электромагнитных волн (когда проволоки были ориентированы параллельно вектору, то решётка пропускала ЭМ волну без помех).
Слайд 67
В 1895 году российский физик экспериментатор-виртуоз П.Н. Лебедев впервые создал комплекс устройств для генерирования и приёма миллиметровых ЭМ волн ( = 4-6 мм ), установил их отражение, двойное преломление, интерференцию. Так были получены ЭМ волны в диапазоне длин волн от 50 мм до 80 мкм, т.е. был перекрыт диапазон между радиоволнами и инфракрасным излучением. ЭМ волны, полученные в описанных экспериментах, имели малую мощность. В 20-х годах генерирование электромагнитных волн стали осуществлять с помощью электроламповых генераторов – автоколебательных систем, позволяющих получать колебания заданной мощности, имеющие синусоидальную форму. В 1923 году профессор Московского университета А.А. Глаголева-Аркадьева сконструировала массовый излучатель в котором короткие ЭМ волны возбуждались колебаниями электрических зарядов в молекулах и атомах. Эти колебания происходили под воздействием искрового разряда, возникающего между металлическим опилками, взвешенными в масле.
Слайд 68
Электромагнитные волны различной длины (частоты) отличаются друг от друга по способам их генерации и регистрации, а также по их свойствам. Диапазоны электромагнитных волн: радиоволны - 10 3 10 -4 м; свет - инфракрасный - 5. 10 -4 8. 10 -7 м; видимый - 8. 10 -7 4. 10 -7 м; ультрафиолетовый - 4. 10 -7 10 -9 м; рентгеновское излучение - 2. 10 -9 6. 10 -12 м; -излучение - менее 6. 10 -12 м. В 1888 году русский физик А.С.Попов повторил опыты Герца, а в 1889 году впервые указал на возможность их использования для передачи сигналов на расстояние. В 1894 году он сконструировал генератор электромагнитных колебаний и когерер - элемент приёмника электромагнитных волн. 7 мая 1895 года продемонстрировал на заседании Российского физико-химического общества радиоприёмник (грозоотметчик), а 24 марта 1896 года наглядно продемонстрировал при помощи своих приборов передачу сигналов на расстояние 250 м. Первая в мире радиограмма состояла из двух слов - «Генрих Герц». В 1898 году в Одессе Н.Д.Пильчиков впервые продемонстрировал радиоуправляемые часы.
Последний слайд презентации: Раздел 4 Колебания и волны
5.3.9. Энергия электромагнитных волн. Поток энергии. Вектор Умова-Пойнтинга. Материальность электромагнитного поля. Объёмная плотность энергии электромагнитной волны равна сумме объёмных плотностей энергии электрического поля и магнитного поля : Поскольку то Модуль плотности потока энергии электромагнитной волны равен: S = w v = E H (здесь v - фазовая скорость). Вектор плотности потока энергии электромагнитной волны параллелен вектору скорости, называется вектором Умова-Пойнтинга и равен: Таким образом, электромагнитные волны, как и любой другой вид материи, обладают энергией, а значит и импульсом. Они оказывают давление на поверхности, на которые падают, что подтвердил своими блестящими опытами П.Н.Лебедев.