Первый слайд презентации: Сабақтың тақырыбы :
Сан аралықтардың бірігуі мен қиылысуы
Слайд 2: Сабақтың мақсаты:
6.2.2.7 сан аралықтарын жазу үшін белгілеулерді пайдалану; 6.2.2.8 сан аралықтарды кескіндеу; 6.2.2.9 сан аралықтардың бірігуін және қиылысуын табу;
Слайд 3: Сабақтың мақсаты:
сан аралықтарын жазу үшін белгілеулерді пайдалану; сан аралықтарды кескіндеу.
Слайд 4: Миға шабуыл"
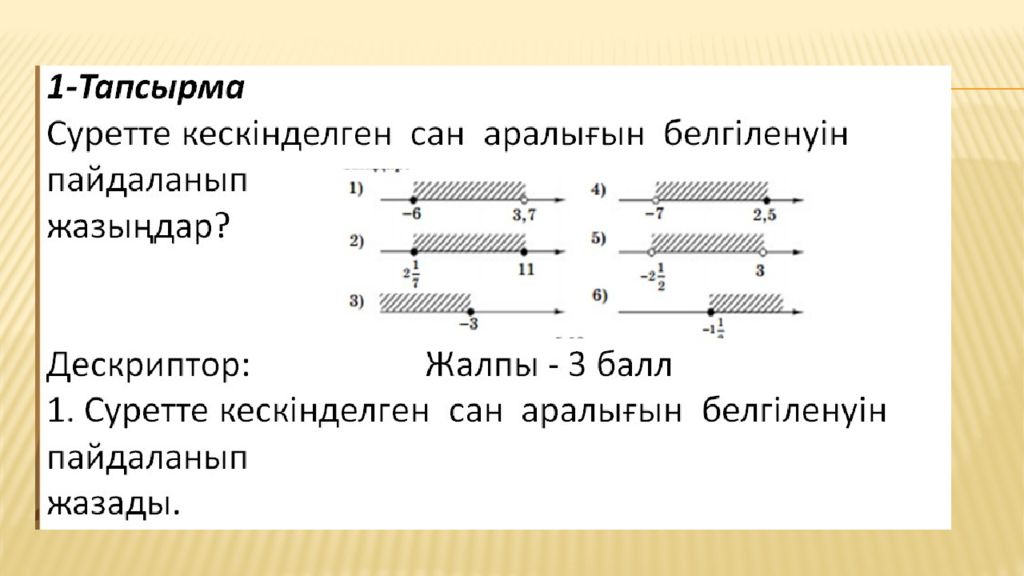
1),Сан аралықтары дегеніміз не? 2)Сан аралығының қандай түрлерін білесіңдер ? 3)Қатаң теңсіздіктің шешімдер жиыны координаталық түзуде қалай кескінделеді? 4) Қатаң емес теңсіздіктің сан аралығын жазу үшін қандай жақша қолданылады? 5)Неліктен кесіндіде координаталық түзуде көрсетілген сандар шешімдер жиынына кіреді?
Слайд 5: Сан аралықтарының қиылысуы ∩ А ∩ В қиылысу белгісі
Мысал 1. (– ∞; 3] және [– 4; +∞) сан аралықтарының қиылысу аралығын табайық. Жазылуы: (– ∞; 3] ∩ [– 4; +∞) = ? Мысал 2. Сан аралықтарының қиылысуы. [-2;4] және [1;6] сан аралықтарының қиылысуы - [1;4]. Бұл олардың ортақ сан аралығы. Белгіленуі: [-2;4] ∩ [1;6 ]= ? [– 4; 3]. [1;4]
Слайд 6: Бүгінгі сабақта НЕ ҮЙРЕНДІМ ?
сан аралықтарын жазу үшін белгілеулерді пайдалану сан аралықтарды кескіндеу
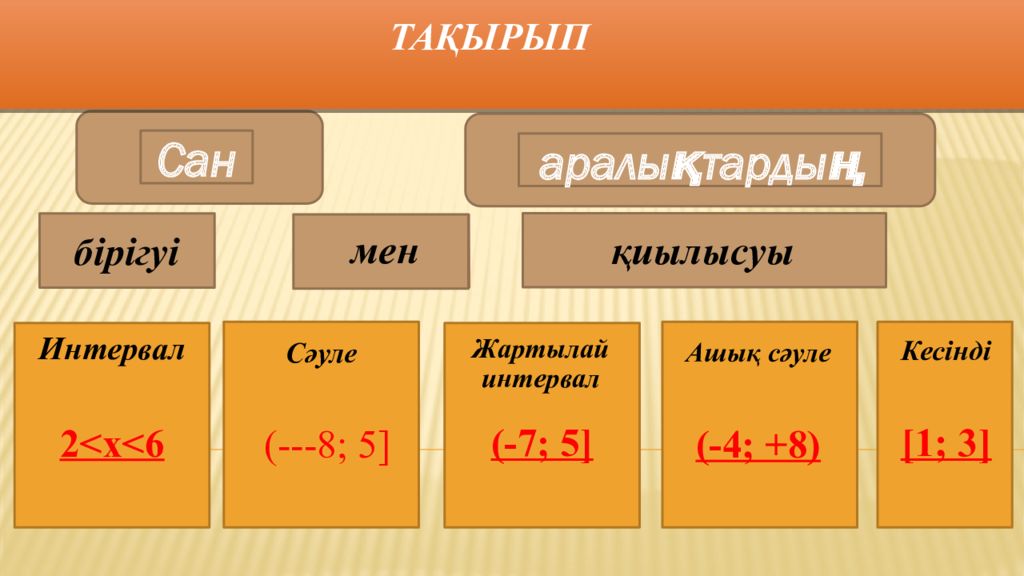
Слайд 7: Та қырып
2<x<6 (---8; 5] Сан аралы қтардың Та қырып Интервал Сәуле Жартылай интервал Ашы қ сәуле Кес інді (---8; 5] 2 <x<6 [1; 3] б ірігуі [1; 3] (-4; +8) мен (-4; +8) (-7; 5] қиылысуы (-7; 5]
Слайд 9
2-тапсырма. 1. Бірінші жәшіктегі мандариндер саны екінші жәшіктегі мандарин-дер санынан 25%-ке артық. Бірінші жәшіктен 6 мандаринді алып, оның жартысын екінші жәшіктегі мандариндерге қосқанда, екі жәшіктегі мандариндер саны бірдей болады. Алғашқыда екінші жәшікте неше мандарин болған? Дескриптор : Жалпы - 3 балл 1. Алғашқыда екінші жәшікте неше мандарин болғанын есептеп шығарады.
Слайд 10: РЕФЛЕКСИЯ
« Аяқталмаған сөйлем » әдісі. Жеке жұмыс: - бүгінгі сабақта мен .... түсіндім,...білдім,....көзімді жеткіздім. - бүгін сабақта қуантқаны..... - мен өзімді.....үшін мақтар едім. - маған ерекше ұнағаны..... - сабақтан соң маған........келді - бүгін маған..........сәті түсті. «Бас бармақ » әдісі арқылы бағаланады.