САНКТ-ПЕТЕРБУРГ о3.о3.2о25 ФИНАНСОВЫЙ МЕНЕДЖМЕНТ Тема 3. Риск и доходность. Модель ценообразования финансовых активов ( Capital Asset Pricing Model, CAPM)
Какова стоимость облигации с погашением через 2 года, ставкой купона 4% и номинальной стоимостью 1000 рублей, если ставка доходности составляет 6 %? Решаем дома и публикуем В k,,,
2 ОСНОВНЫЕ ВОПРОСЫ ТЕМЫ Для чего это нужно? Чтобы оценивать стоимость капитала / требуемую доходность для инвестиций … … чтобы потом ее использовать для нахождения NPV инвестиций
3 ГЛАВНОЕ ИЗ ПРОШЛОЙ ТЕМЫ Инвестиция / проект – денежные потоки Будущие денежные потоки оцениваются с помощью приведенной стоимости ( Prevent Value, PV) – ценность денежных потоков с позиции сегодня Каждый проект можно оценить, вычтя из PV будущих потоков требуемые сегодняшние инвестиции, т.е., посчитав чистую приведенную стоимость
4 ГЛАВНОЕ ИЗ ПРОШЛОЙ ТЕМЫ Ставку дисконтирования i можно рассматривать как альтернативные издержки капитала или стоимость капитала ( opportunity cost of capital) какую доходность инвестор «упускает», предпочтя проект инвестиции на рынке с таким же риском и горизонтом Другой термин для i : требуемая доходность ( required return), т.е. минимальная доходность, на которую согласен инвестор, вкладывающийся в проект Мы рассматривали безрисковые инвестиции, i = i f, но эти определения применимы для любых инвестиций
5 ПОНЯТИЕ НЕОПРЕДЕЛЕННОСТИ И РИСКА ЧТО ЕСЛИ ДЕНЕЖНЫЕ ПОТОКИ СЛУЧАЙНЫ? Как оценить приведенную стоимость таких потоков и NPV инвестиции? Простой неправильный способ: - взять средний CF 1 : ( 1/2)*80 + (1/2)*160 = 120 - продисконтировать 120 по безрисковой ставке
6 ПОНЯТИЕ НЕОПРЕДЕЛЕННОСТИ И РИСКА НЕОПРЕДЕЛЕННОСТЬ И РИСК Чтобы вы предпочли? Как правило, для заданного среднего значения (мат. ожидания) люди предпочитают гарантированные деньги неопределенным – это отвращение к риску, неприятие риска ( Risk Aversion) Гарантированно 100 000 руб. «Лотерея» Орел Решка 200 000 руб. 0 руб.
7 ПОНЯТИЕ НЕОПРЕДЕЛЕННОСТИ И РИСКА НЕОПРЕДЕЛЕННОСТЬ И РИСК Можно померить отвращение к риску. Например: на какую минимальную гарантированную сумму вы готовы променять «лотерею»? Допустим 92 000 рублей. Тогда: - 92 000 – безрисковый эквивалент «лотереи» ( Certainty Equivalent, CE) - Премия за риск = ожидаемый выигрыш в лотерее – безрисковый эквивалент = 100 000 – 92 000 = 8 000 Гарантированно 100 000 руб. «Лотерея» Орел Решка 200 000 руб. 0 руб.
8 ОТСТУПЛЕНИЕ: МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ Если случайная величина X принимает дискретные значения X 1, X 2, X 3 … X n с вероятностями p 1, p 2, p 3 … p n, то математическое ожидание – это Для непрерывно распределенных случайных величин формула аналогична, но вместо суммы – интеграл, а вместо вероятностей – плотность вероятности, но мы будем работать с дискретными величинами
9 ПОНЯТИЕ НЕОПРЕДЕЛЕННОСТИ И РИСКА КАК УЧЕСТЬ РИСК ПРИ ОЦЕНКЕ ОЖИДАЕМОГО ДЕНЕЖНОГО ПОТОКА? Два способа: - Посчитать безрисковый эквивалент для денежных потоков, применить безрисковую ставку дисконтирования - Применить более высокую ставку дисконтирования к ожидаемым денежным потокам (1+ )
10 ПОНЯТИЕ НЕОПРЕДЕЛЕННОСТИ И РИСКА КАК УЧЕСТЬ РИСК ПРИ ОЦЕНКЕ ОЖИДАЕМОГО ДЕНЕЖНОГО ПОТОКА? На практике: 2 способ Откуда взять ставку?? Примечание: рискованные потоки необязательно должны дисконтироваться по ставке выше безрисковой
11 ПОНЯТИЕ НЕОПРЕДЕЛЕННОСТИ И РИСКА ОТКУДА ВЗЯТЬ СТАВКУ? ОБЩАЯ ИДЕЯ Посмотреть на финансовый рынок Найти ценную бумагу (или комбинацию, портфель) с «таким же риском» как наш проект Оценить ее ожидаемую доходность – это и будет требуемая доходность для проекта Но как найти такую бумагу? Что значит «с таким же риском»?
12 ПОНЯТИЕ НЕОПРЕДЕЛЕННОСТИ И РИСКА ОЖИДАЕМАЯ ДОХОДНОСТЬ ОДНОПЕРИОДНОЙ ИНВЕСТИЦИИ Доход CF 1 - I 0 Доходность Обозначим Е( CF 1 ) – мат. ожидание потоков Ожидаемая доходность
13 ПОНЯТИЕ НЕОПРЕДЕЛЕННОСТИ И РИСКА ОЖИДАЕМАЯ ДОХОДНОСТЬ ОДНОПЕРИОДНОЙ ИНВЕСТИЦИИ I 0 100 Вероятность ½ ½ CF 1 80 160 Доходность, R Мат. ожидание CF 1, E(CF 1 ) ½*80+½*160 = 120 Ожидаемая доходность, E(R)
1 4 ПОНЯТИЕ НЕОПРЕДЕЛЕННОСТИ И РИСКА ОЖИДАЕМАЯ ДОХОДНОСТЬ ОДНОПЕРИОДНОЙ ИНВЕСТИЦИИ Замечание: не путать ожидаемую доходность инвестиции и требуемую доходность Требуемая доходность – ставка, по которой нужно дисконтировать денежные потоки, чтобы получит из PV Ожидаемая доходность может быть: выше требуемой ↔ NPV инвестиции > 0 ниже требуемой ↔ NPV < 0
15 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ ОЖИДАЕМАЯ ДОХОДНОСТЬ НА ФИНАНСОВОМ РЫНКЕ На финансовом рынке: I 0 =P 0 – сегодняшняя цена бумаги (например, акции) или портфеля бумаг (например, 2-х облигаций Газпрома и 1-й акций Google) Будущая стоимость P t – будущая цена ценной бумаги Выплаты инвесторам - Купонные выплаты C t в случае облигаций (если нет дефолта) - Дивиденды Div t в случае акций
16 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ ОЖИДАЕМАЯ ДОХОДНОСТЬ НА ФИНАНСОВОМ РЫНКЕ Тогда доходность бумаги на финансовом рынке за один период на примере акции: Ожидаемая доходность:
17 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ Ближайшая цель: понять, как связан риск финансового инструмента с его доходностью Узнав это и оценив риск нашего проекта, мы сможем узнать требуемую доходность для проекта Стандартные меры риска: дисперсия и «волатильность» доходности
18 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ ДИСПЕРСИЯ И СТАНДАРТНОЕ ОТКЛОНЕНИЕ (ВОЛАТИЛЬНОСТЬ) ДОХОДНОСТИ Дисперсия доходности: Стандартное отклонение доходности: Смысл: мера того, насколько велик ожидаемый разброс значений доходности относительно ожидаемого значения
19 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ ДИСПЕРСИЯ И ВОЛАТИЛЬНОСТЬ ДОХОДНОСТИ. ПРИМЕР АКЦИИ P 0 100 Вероятности ½ ½ P 1 + Div 1 80 160 R -20% 60%
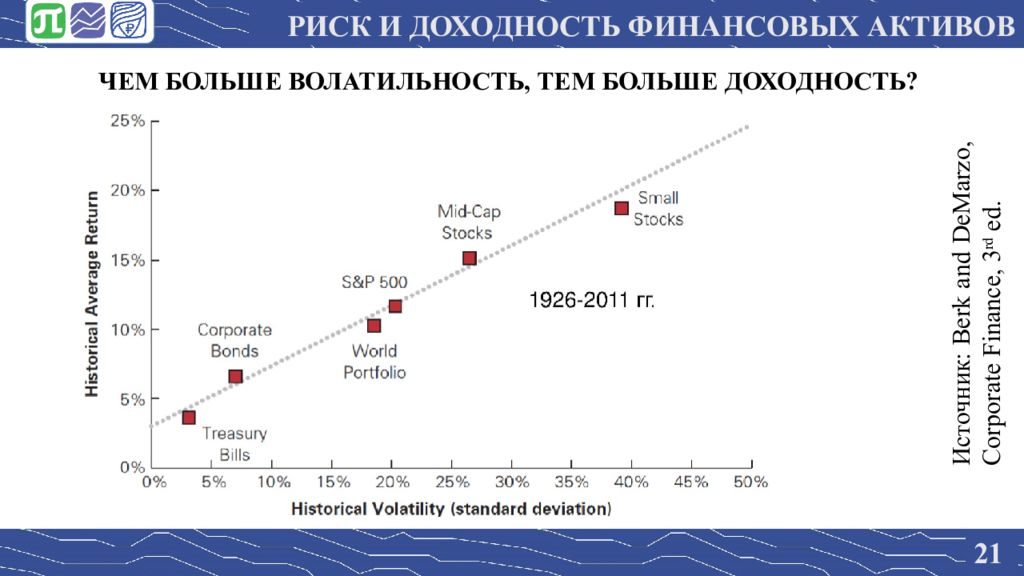
2 0 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ ЧЕМ БОЛЬШЕ ВОЛАТИЛЬНОСТЬ, ТЕМ БОЛЬШЕ ДОХОДНОСТЬ? Например, две акции: А и В Пусть за один год ни одна из них не приносит дивидендов Акция А будет стоить 105 р. точно Акция В через год будет стоить либо 100 р. либо 110 р. с равными вероятностями Таким образом: ожидаемая будущая стоимость А и В одинакова Верно ли утверждение: Акция В сегодня должна стоить меньше А, т.е., ее ожидаемая доходность должна быть выше, т.к. она волатильнее ?
2 1 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ ЧЕМ БОЛЬШЕ ВОЛАТИЛЬНОСТЬ, ТЕМ БОЛЬШЕ ДОХОДНОСТЬ? Источник: Berk and DeMarzo, Corporate Finance, 3 rd ed.
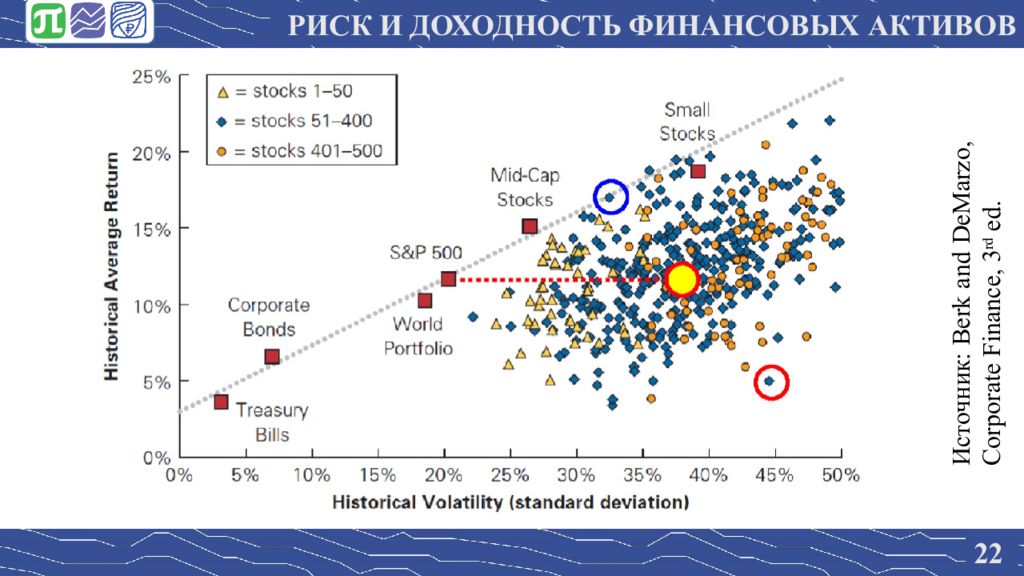
2 2 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ Источник: Berk and DeMarzo, Corporate Finance, 3 rd ed.
2 3 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ Два наблюдения из графика: Волатильность больше портфеля акций ниже волатильности каждой акции Менее волатильные акции могут иметь бОльшую ожидаемую доходность! Интуитивное объяснение 1-го наблюдения: диверсификация Объяснение 2-го наблюдения?
2 4 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ Пусть есть акции 2-х фирм: А и В Обе стоят 100 р. и приносят доходность -20% и 60% с равными вероятностями Доходности А и В независимы друг от друга (вероятность высокой доходности одной не зависит от реализации другой) ДИВЕРСИФИКАЦИЯ РИСКА Акция А P 0 100 р. Вероятности ½ ½ P 1 +Div 1 80 160 R -20% 60% E(R) 20% SD(R) 40% Акция B P 0 100 р. Вероятности ½ ½ P 1 +Div 1 80 160 R -20% 60% E(R) 20% SD(R) 40%
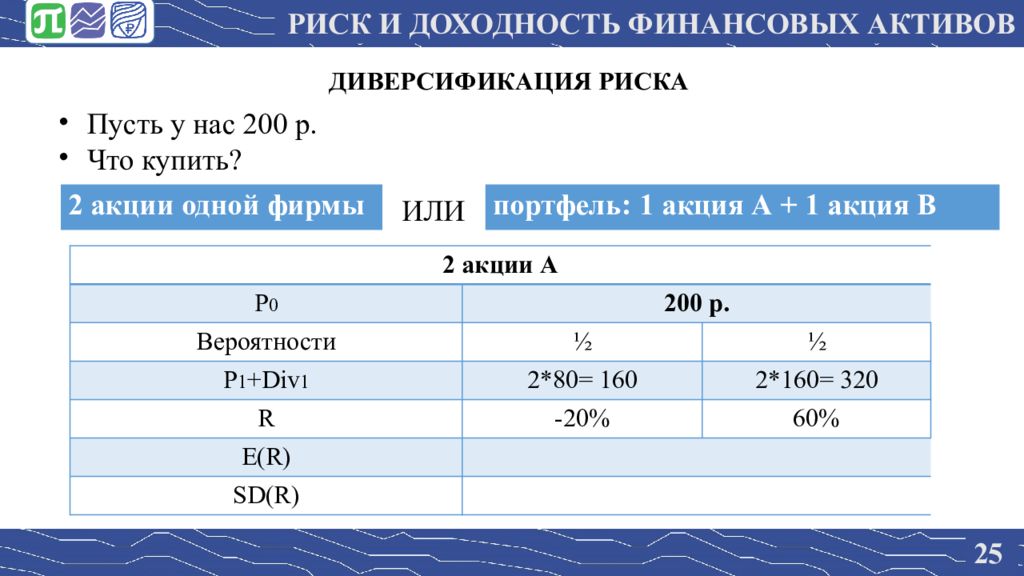
25 Пусть у нас 200 р. Что купить? ДИВЕРСИФИКАЦИЯ РИСКА 2 акции А P 0 2 00 р. Вероятности ½ ½ P 1 +Div 1 2* 80 = 160 2* 160 = 320 R -20% 60% E(R) SD(R) 2 акции одной фирмы ИЛИ портфель: 1 акция А + 1 акция В РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
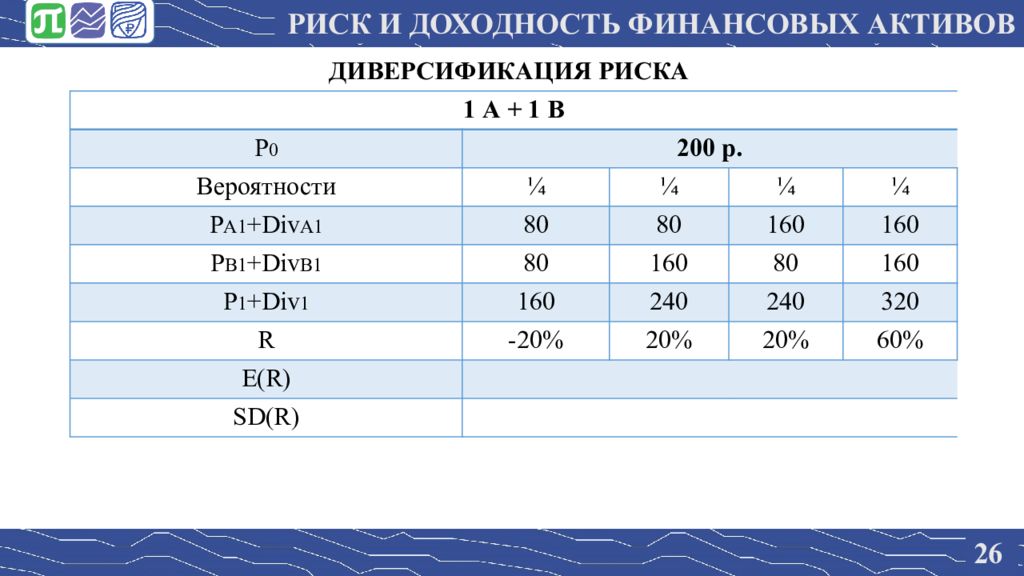
26 ДИВЕРСИФИКАЦИЯ РИСКА 1 А + 1 В P 0 2 00 р. Вероятности ¼ ¼ ¼ ¼ P А1 + Div А1 80 80 160 160 P В1 + Div В1 80 160 80 160 P 1 + Div 1 160 240 240 320 R -20% 20% 20% 60% E(R) SD(R) РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
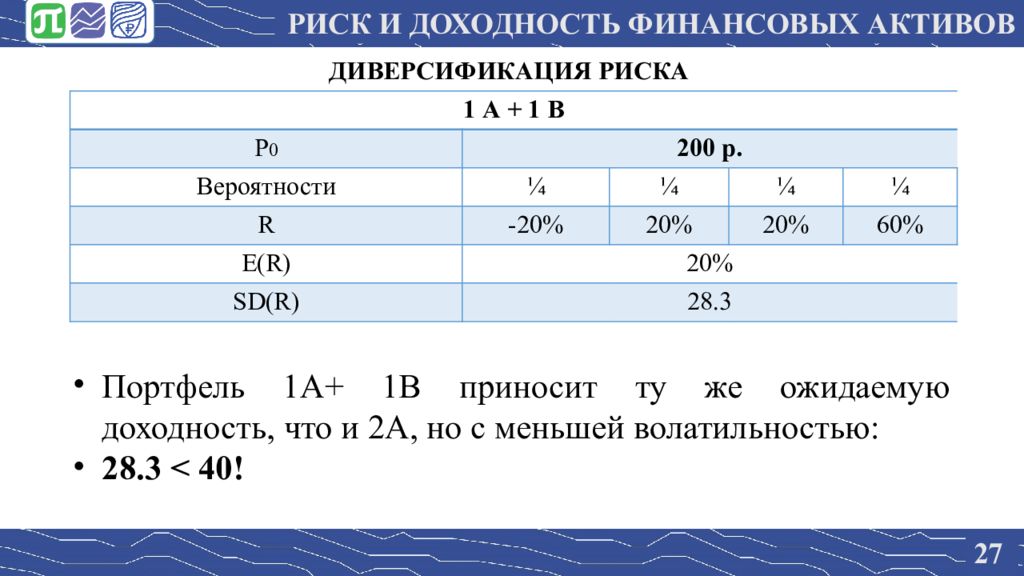
2 7 ДИВЕРСИФИКАЦИЯ РИСКА 1 А + 1 В P 0 2 00 р. Вероятности ¼ ¼ ¼ ¼ R -20% 20% 20% 60% E(R) 20% SD(R) 28.3 Портфель 1А+ 1В приносит ту же ожидаемую доходность, что и 2А, но с меньшей волатильностью: 28.3 < 40! РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
28 ДИВЕРСИФИКАЦИЯ РИСКА С ростом n дисперсия (и волатильность) уменьшается и стремится к 0 при n →∞ - полная диверсификация → Доходность такого портфеля ( n =∞) должна быть безрисковой, иначе можно было бы делать «арбитраж» Если E( Rp )> i f, инвестор мог бы взять в долг под if и вложить в портфель, заработав «бесплатную» гарантированную прибыль Если E( Rp )< i f, инвестор мог бы продать портфель (возможно «в короткую») и вложить деньги в безрисковые облигации под i f, заработав «бесплатную» гарантированную прибыль Такие бы действия оказали давление на цены инструментов так, что E( Rp ) и i f выровнялись бы Что будет, если акций с независимыми друг от друга доходностями будет 10? 1000? ∞? РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
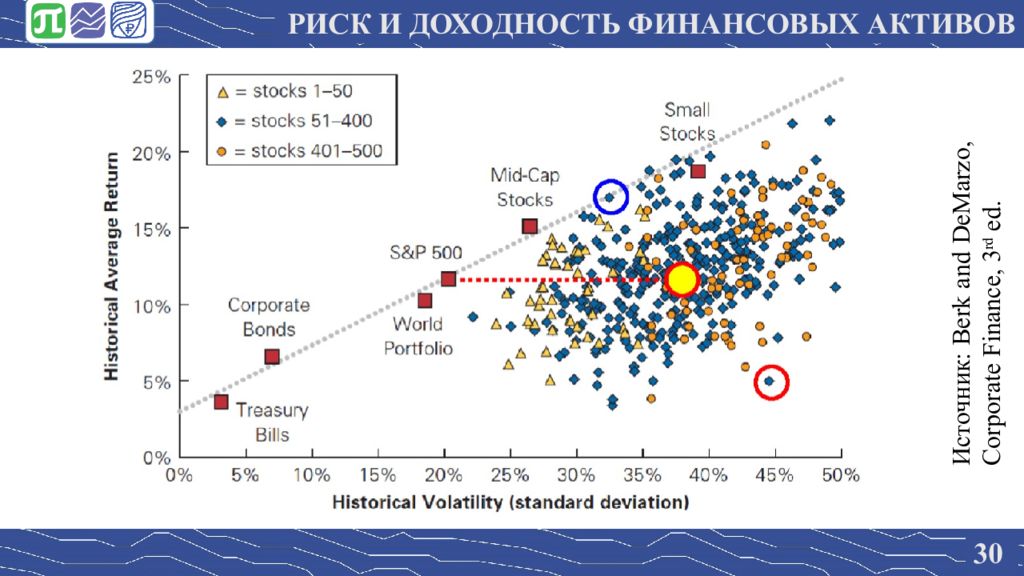
29 ДИВЕРСИФИКАЦИЯ РИСКА Д оходность акции даже с большой волатильностью может быть мала и близка к безрисковой ! → Интуитивная догадка: на самом деле доходность акции определяется не только ее волатильностью, сколько способностью улучшать диверсификацию портфеля Почему же волатильность большого портфеля акций ( S&P 500) сильно отличается от нуля, а доходность – от безрисковой ? Ответ: корреляция между доходностями акций - Акция А и другая акция А полностью коррелированы, «портфель» из двух акций А никак не уменьшил риск РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
30 Источник: Berk and DeMarzo, Corporate Finance, 3 rd ed. РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
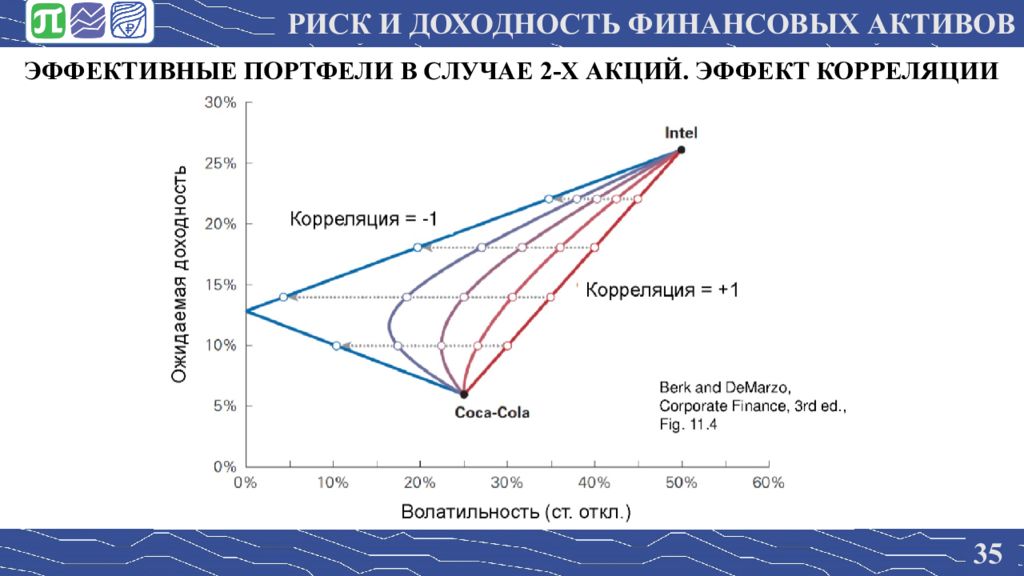
31 КОРРЕЛЯЦИЯ И ДИВЕРСИФИКАЦИЯ. ПРИМЕР 2-Х БУМАГ Положительная корреляция мешает диверсификации Отрицательная корреляция – помогает Корреляция всегда лежит от -1 до 1 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
32 ДИВЕРСИФИКАЦИЯ, КАК ИЗБАВЛЕНИЕ ОТ ИДИОСИНКРАТИЧЕСКОГО РИСКА Риск ценной бумаги: Идиосинкратический (специфический для фирмы) Колебания доходности, связанные с новостями непосредственно о данной компании (компания получила патент, уволился гендиректор, авария на платформе…) Системный (рыночный) Колебания, вызванные глобальными факторами, влияющими на весь рынок (цена на нефть, война, изменение процентной ставки) Диверсификация позволяет избавиться от идиосинкратического, но не от системного риска, т.к. именно системный риск ответственен за корреляцию доходностей РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
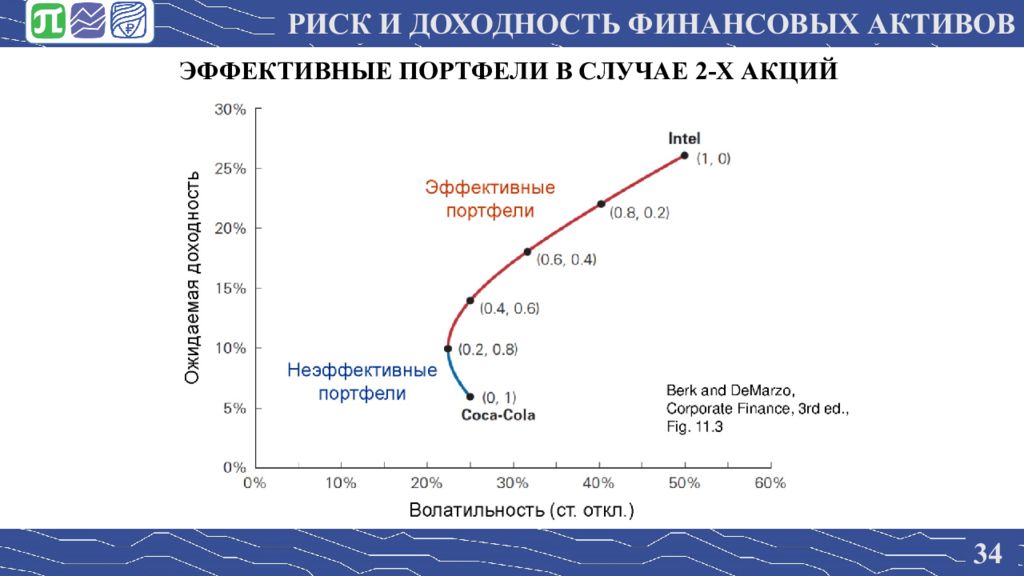
33 Пример 2-х акций (из Berk, DeMarzo, 3 rd ed., ch. 11) КАКОЙ ЖЕ ПОРТФЕЛЬ БУДУТ ДЕРЖАТЬ ИНВЕСТОРЫ? Акция E(R) SD(R) Intel 26% 50% Coca-Cola 6% 25% Рассмотрим портфель: x% Intel, (100-x)% Coca-Cola Пусть корреляция между доходностями = 0 Цель: - ожидаемая доходность как можно больше, - волатильность как можно меньше РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
34 ЭФФЕКТИВНЫЕ ПОРТФЕЛИ В СЛУЧАЕ 2-Х АКЦИЙ РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
35 ЭФФЕКТИВНЫЕ ПОРТФЕЛИ В СЛУЧАЕ 2-Х АКЦИЙ. ЭФФЕКТ КОРРЕЛЯЦИИ РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ
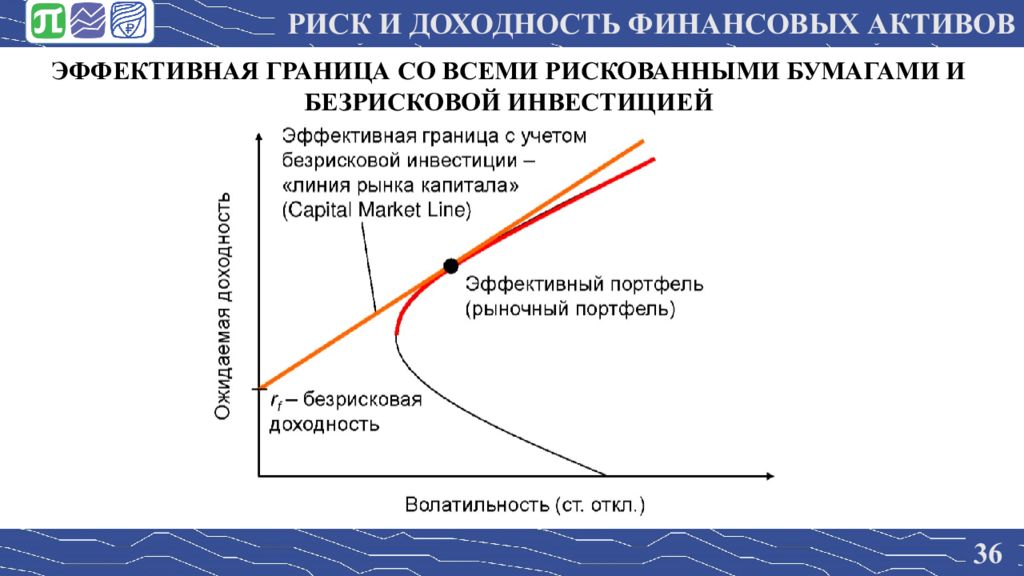
36 РИСК И ДОХОДНОСТЬ ФИНАНСОВЫХ АКТИВОВ ЭФФЕКТИВНАЯ ГРАНИЦА СО ВСЕМИ РИСКОВАННЫМИ БУМАГАМИ И БЕЗРИСКОВОЙ ИНВЕСТИЦИЕЙ
37 Каждый инвестор держит комбинацию эффективного портфеля и безрискового актива – т.е., выбирает точку на «линии рынка капитала» Какую конкретно – зависит от отношения инвестора к риску Эффективный портфель включает в себя все бумаги, существующие на рынке – рыночный портфель Если есть бумага, не входящая в эффективный портфель, значит ее никто не держит → значит ее нет! Ожидаемая доходность каждой бумаги определяется ее вкладом в волатильность эффективного портфеля, т.е. ее способностью улучшить диверсификацию портфеля МОДЕЛЬ ЦЕНООБРАЗОВАНИЯ ФИНАНСОВЫХ АКТИВОВ
38 Ожидаемая доходность каждой бумаги определяется ее вкладом в волатильность эффективного портфеля или, эквивалентно, ее чувствительностью к рыночному риску – коэффициентом бета R Mkt – доходность рыночного портфеля Бета – «чувствительность» к колебаниям рынка Интуитивно: большая чувствительность – слабая роль к диверсификации, большой вклад в волатильность → нужна компенсация за риск → большая ожидаемая доходность МОДЕЛЬ ЦЕНООБРАЗОВАНИЯ ФИНАНСОВЫХ АКТИВОВ
39 МОДЕЛЬ ЦЕНООБРАЗОВАНИЯ ФИНАНСОВЫХ АКТИВОВ
40 ИТОГ Ожидаемая доходность ценной бумаги определяется: Безрисковой ставкой доходности Рыночной премией – превышением ожидаемой доходности рыночного портфеля над безрисковой ставкой Коэффициент бета - чувствительностью бумаги к рыночному риску Правильная мера риска бумаги - бета МОДЕЛЬ ЦЕНООБРАЗОВАНИЯ ФИНАНСОВЫХ АКТИВОВ
41 МОДЕЛЬ ЦЕНООБРАЗОВАНИЯ ФИНАНСОВЫХ АКТИВОВ ЗАМЕЧАНИЯ Если бумага рискованная, но не коррелирована с рынком, ее доходность = безрисковой Поскольку сама бумага тоже входит в портфель, нулевая корреляция с рынком означает отрицательную корреляцию с рыночным портфелем, из которого выключена эта бумага – это и говорит о способности бумаги к участию к диверсификации Негативная бета ↔ E(R) < r f. CAPM объясняет, почему могут быть рискованные инструменты с ожидаемой доходностью ниже безрисковой. Теория предполагает, что инвесторы не ограничены в возможностях диверсификации. Если это не так, премия за риск будет зависеть и от специфического риска бумаги
42 Доходность акции равновероятно принимает значения -5% и 15%. Какого стандартное отклонение доходности данной акции? Для какого портфеля коэффициент бета равен 1 ? Решаем дома и публикуем В k,,,
Спасибо за внимание!
