Слайд 2
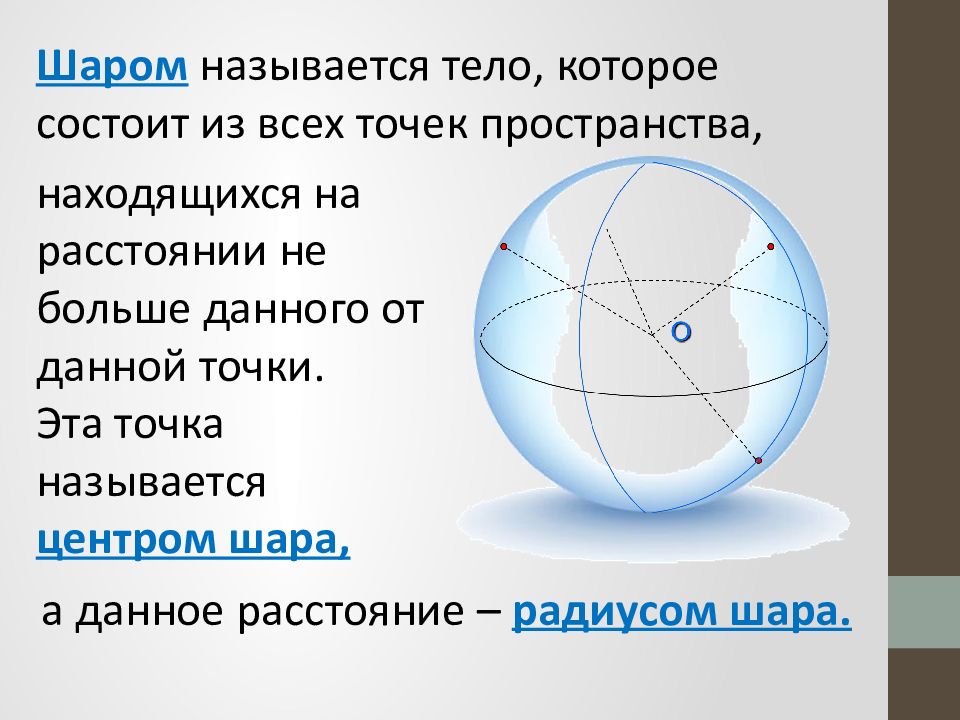
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии не больше данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара.
Слайд 3
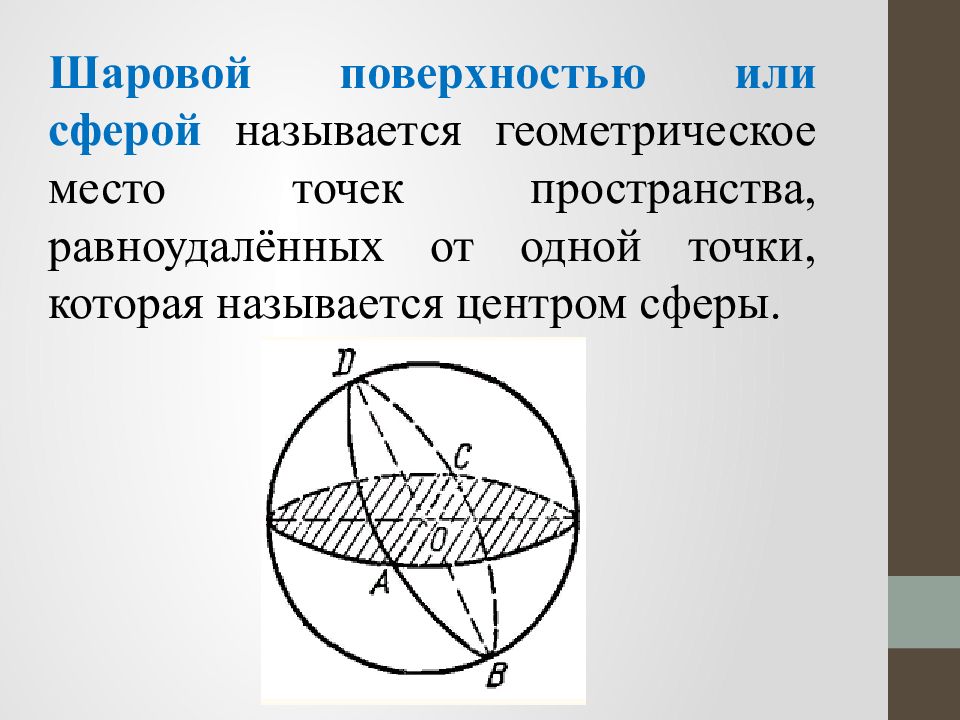
Шаровой поверхностью или сферой называется геометрическое место точек пространства, равноудалённых от одной точки, которая называется центром сферы.
Слайд 4
Радиусом сферы называется отрезок прямой, который соединяет центр сферы с любой её точкой, например АО = ОВ = R.
Слайд 5
Хордой сферы называется отрезок прямой, который соединяет две её любых точки. Диаметром сферы называется хорда, которая проходит через её центр, например АС или ВD. Концы любого диаметра называют диаметрально противоположными точками сферы. Шаром называется тело, ограниченное сферой. Сферу можно получить вращением полукруга вокруг диаметра
Слайд 7
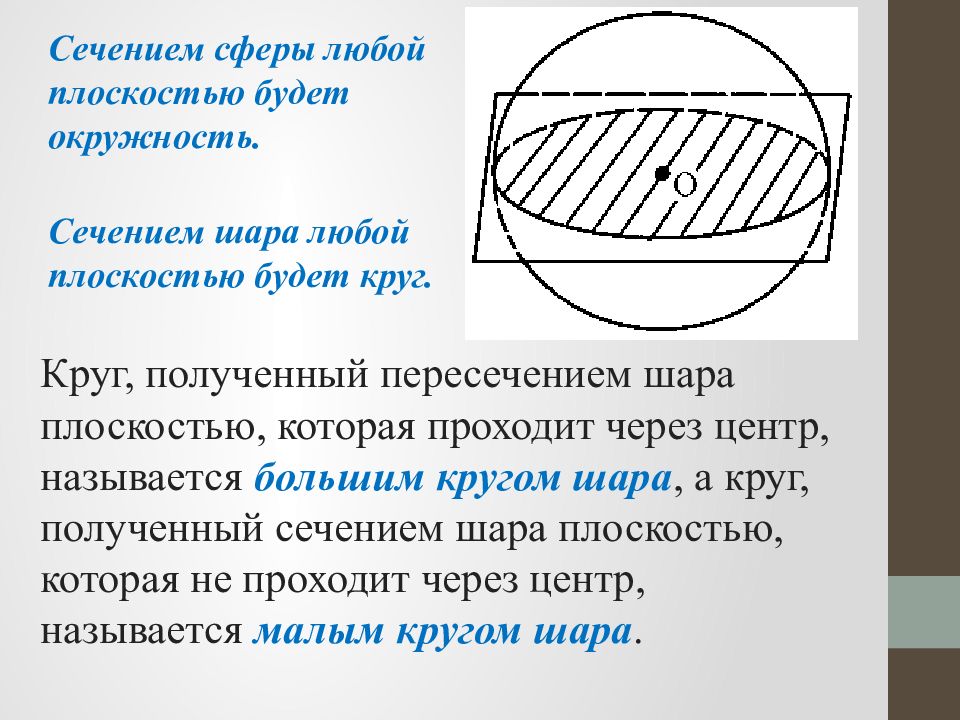
Сечением сферы любой плоскостью будет окружность. Сечением шара любой плоскостью будет круг. Круг, полученный пересечением шара плоскостью, которая проходит через центр, называется большим кругом шара, а круг, полученный сечением шара плоскостью, которая не проходит через центр, называется малым кругом шара.
Слайд 8
Сечения равноудалённые от центра шара, равны между собой. Из двух сечений, не одинаково удалённых от центра шара, больший радиус имеет то, которое лежит ближе к центру. Любая плоскость, которая проходит через центр шара, делит его поверхность на две симметричные и равные части. Через две точки сферы, которые не лежат на концах одного диаметра, можно провести окружность большого круга, и только одну. Окружности двух больших кругов при пересечении делятся пополам.
Слайд 9: Плоскость, касательная к шару
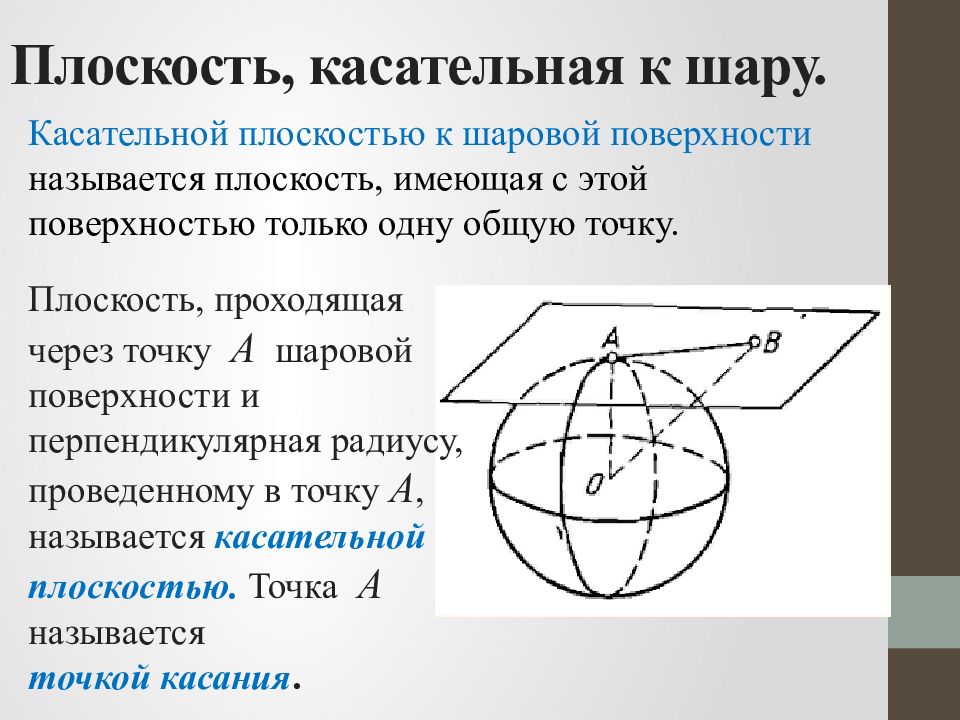
Касательной плоскостью к шаровой поверхности называется плоскость, имеющая с этой поверхностью только одну общую точку. Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью. Точка А называется точкой касания.
Слайд 10
Касательная плоскость имеет с шаром только одну общую точку – точку касания. Прямая в касательной плоскости шара, которая проходит через точку касания, называется касательной шара в этой точке. Так как касательная плоскость имеет с шаром только одну общую точку, то касательная прямая тоже имеет с шаром только одну общую точку – точку касания.
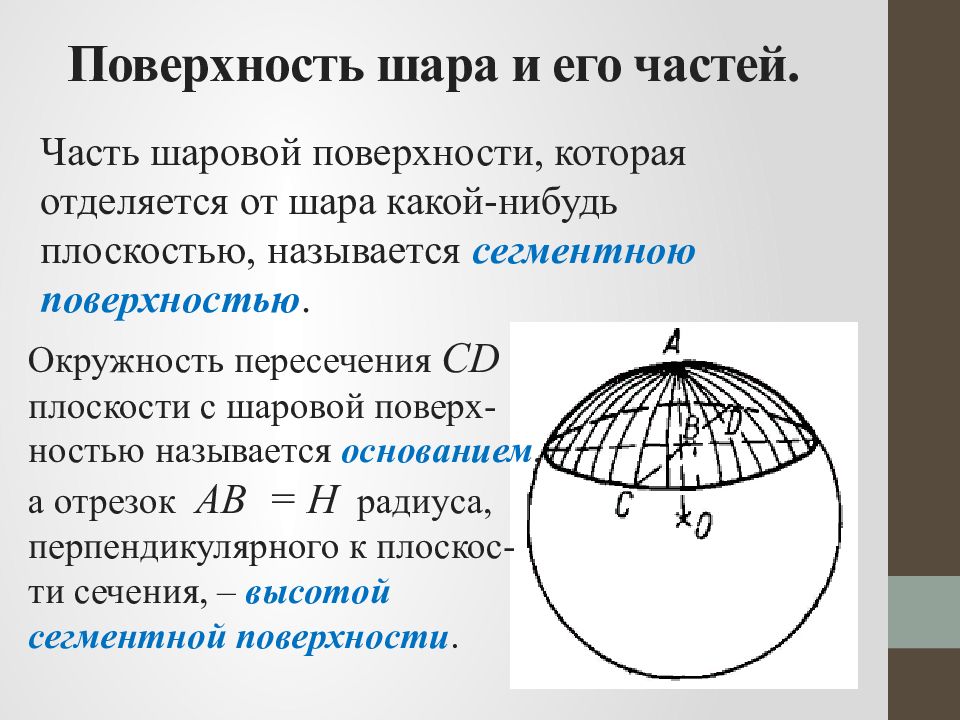
Слайд 11: Поверхность шара и его частей
Часть шаровой поверхности, которая отделяется от шара какой-нибудь плоскостью, называется сегментною поверхностью. Окружность пересечения СD плоскости с шаровой поверх- ностью называется основанием, а отрезок АВ = Н радиуса, перпендикулярного к плоскос-ти сечения, – высотой сегментной поверхности.
Слайд 12
Часть шаровой поверхности, заключённая между двумя параллельными секущими плоскостями, называется шаровым поясом. Окружности сечения С 1 D 1 и С 2 D 2 называются основаниями шарового пояса, а расстояние АВ = Н между параллельными плоскостями – высотой пояса.