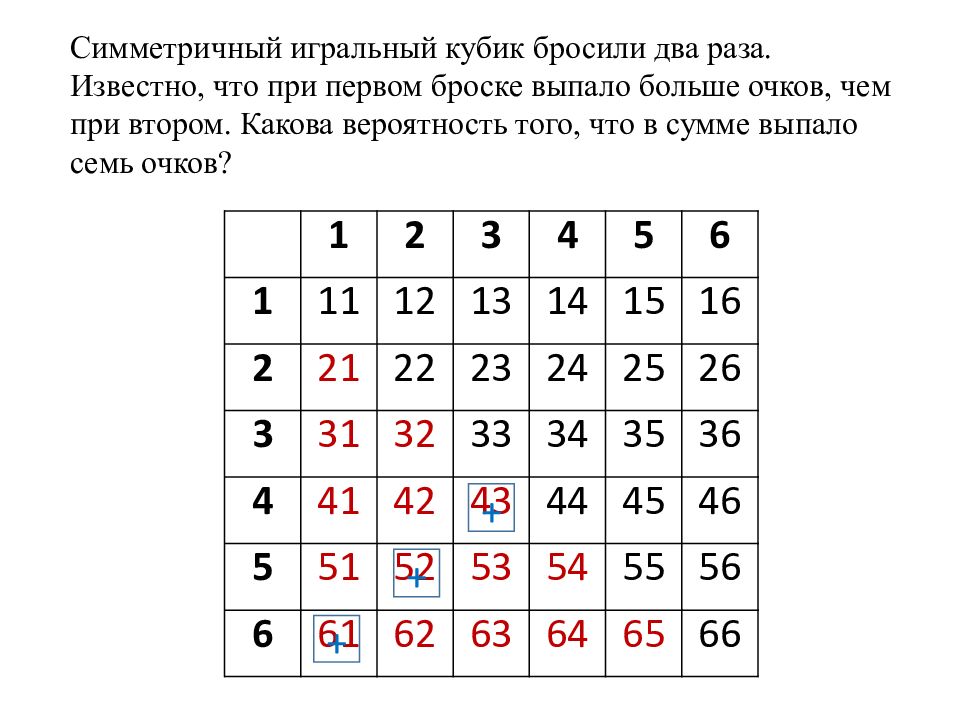
Симметричный игральный кубик бросили два раза. Известно, что при первом броске выпало больше очков, чем при втором. Какова вероятность того, что в сумме выпало семь очков? 1 2 3 4 5 6 1 11 12 13 14 15 16 2 21 22 23 24 25 26 3 31 32 33 34 35 36 4 41 42 43 44 45 46 5 51 52 53 54 55 56 6 61 62 63 64 65 66 + + +
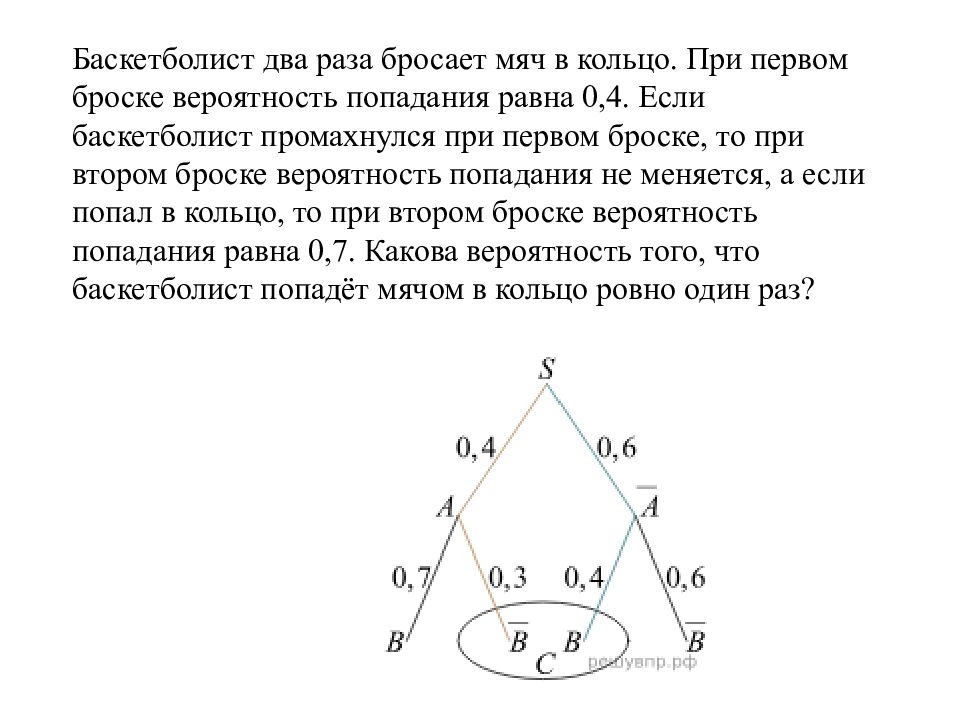
Баскетболист два раза бросает мяч в кольцо. При первом броске вероятность попадания равна 0,4. Если баскетболист промахнулся при первом броске, то при втором броске вероятность попадания не меняется, а если попал в кольцо, то при втором броске вероятность попадания равна 0,7. Какова вероятность того, что баскетболист попадёт мячом в кольцо ровно один раз?
Баскетболист два раза бросает мяч в кольцо. При первом броске вероятность попадания равна 0,4. Если баскетболист промахнулся при первом броске, то при втором броске вероятность попадания не меняется, а если попал в кольцо, то при втором броске вероятность попадания равна 0,7. Какова вероятность того, что баскетболист попадёт мячом в кольцо ровно один раз? Обозначим A и B события «попадание при первом броске» и «попадание при втором броске» соответственно и построим дерево этого случайного опыта. Событию C «ровно одно попадание» благоприятствуют цепи
Вероятность того, что батарейка бракованная, равна 0,03. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными. Найдём вероятность того, что батарейка исправна: 1 – 0,03 = 0,97 Значит, вероятность того, что обе батарейки исправны: 0,97 ٠ 0,97 = 0,9409
Николай Валентинович выбирает интернет-магазин на основе рейтинга надёжности. Вероятность того, что нужный товар доставят из магазина A в течение недели, равна 0,8. Вероятность того, что нужный товар доставят из магазина B в течение недели, равна 0,75. Николай Валентинович заказал товар сразу в двух магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один из магазинов не доставит товар в указанный срок. Решение. Вероятность того, что первый магазин не доставит нужный товар в течение недели равна 1 − 0,8 = 0,2. Вероятность того, что второй магазин не доставит нужный товар в течение недели равна 1 − 0,75 = 0,25. Поскольку эти события независимы, вероятность их произведения (оба магазина не доставят товар в указанный срок) равна произведению вероятностей этих событий: 0,2 · 0,25 = 0,05.
Платежный терминал в течение рабочего дня может выйти из строя. Вероятность этого события 0,07. В торговом центре независимо друг от друга работают два таких платёжных терминала. Найдите вероятность того, что хотя бы один из них в течение рабочего дня будет исправен. Решение. Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,07 · 0,07 = 0,0049. Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0049 = 0,9951.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,21. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит. Решение. Найдем вероятность того, что перегорят три лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,21·0,21·0,21 = 0,009261. Событие, состоящее в том, что не перегорит хотя бы одна лампа — противоположное. Следовательно, его вероятность равна 1 − 0,009261 = 0,990739.
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,03 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. Решение. Найдем вероятность того, что неисправны оба автомата. Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий: 0,03 · 0,03 = 0,0009. Событие, состоящее в том, что исправен хотя бы один автомат, противоположное. Следовательно, его вероятность равна 1 − 0,0009 = 0,9991.
Какова вероятность того, что в случайно выбранном телефонном номере последняя цифра чётная, а предпоследняя — нечётная? Решение: Вероятность того, что на последнем месте окажется чётное число, равна 0,5. Вероятность того, что на предпоследнем месте окажется нечётное число, равна 0,5. Следовательно, вероятность того, что в случайно выбранном телефонном номере последняя цифра чётная, а предпоследняя — нечётная, равна 0,5 · 0,5=0,25.
В коробке 8 синих, 6 красных и 11 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер? Решение. Возможны два случая: сначала выбрали синий фломастер, потом красный, или сначала выбрали красный фломастер, потом синий. Эти события несовместны, поэтому искомая вероятность равна:
Садовник принес две корзинки фруктов. В одной из них 2 яблока и 6 персиков, а в другой — 8 яблок и 12 персиков. Хозяйка, не глядя, взяла из каждой корзинки по одному фрукту. Какова вероятность того, что она достала два яблока или два персика? Решение. Вероятность того, что хозяйка достала два яблока равна Вероятность того, что хозяйка достала два персика равна Вероятность того, что хозяйка достала два яблока или два персика равна сумме вероятностей этих событий:
Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что биатлонист первые 4 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых. Решение. Поскольку биатлонист попадает в мишени с вероятностью 0,9, он промахивается с вероятностью 1 − 0,9 = 0,1. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, попал, промахнулся» равна
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Решение. События выиграть белыми и черными фигурами независимы, вероятность произведения независимых событий равна произведению их вероятностей: 0,5 · 0,32 = 0,16.
В магазине три продавца. Каждый из них занят обслуживанием клиента с вероятностью 0,7 независимо от других продавцов. Найдите вероятность того, что в случайный момент времени все три продавца заняты. Решение: Три продавца могут быть заняты независимо друг от друга. Вероятность того, что и первый занят, и второй, и третий занят, — это произведение вероятностей трёх событий.
