Первый слайд презентации: 9 сынып алгебра курсында екі айнымалысы бар сызықты қ емес теңдеулер жүйесін оқыту әдістемесі
Магистрант: Нурмұхан Амандық 2 курс Ғылыми жетекші : Қасқатаева Б.Р. – п.ғ.д., профессор. Абай атындағы Қазақ ұлттық педагогикалық университеті Математика, физика және информатика институты
Слайд 2: 9 сынып алгебра пәнінің оқу бағдарламасы
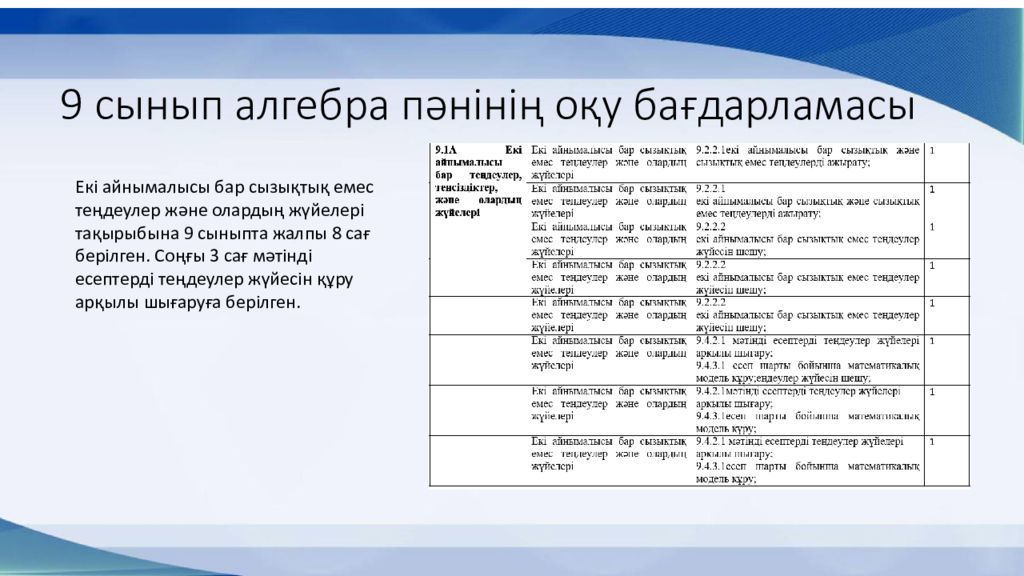
Екі айнымалысы бар сызықтық емес теңдеулер және олардың жүйелері тақырыбына 9 c ыныпта жалпы 8 са ғ берілген. Соңғы 3 са ғ мәтінді есептерді теңдеулер жүйесін құру арқылы шығаруға берілген.
Слайд 3: Екі айнымалысы бар теңдеулер жүйесін шешудің негізгі әдістері:
Алмастыру Алгебралық қосу Жаңа айнымалы еңгізу Графиктік
Слайд 4: 1) Алмастыру
a) Тікелей алмастыру тәсілі 2 – ш і теңдеуден x т і y арқылы өрнектеп алып, 1 – ші теңдеуге қоямыз. Жауабы : (3;1), (-1;-3).
Слайд 5
Ә ) Басқа әдістермен бірге Төменде берілген теңдеулер жүйесі бірден алмастыру тәсіліне келмейді, бірінші мүшелеп қосу ( алу, бөлу,көбейту ) сияқты амалдарды қолдану арқылы қарапайым сызықтық теңдеулер жүйесіне келтіруге болады. Жауабы: ( 0,5 ; 4)
Слайд 6: Жаңа айнымалы енгізу
Жаңа айнымалы енгіземіз : х + у = u, = v Пайда болған теңдеулер жүйесін шешеміз: Жауабы: ( ; ) (4 ; 1)
Слайд 7: Жаңа айнымалы енгізу
Егерде теңдеулер жүйесінде өзара кері өрнектер бар болса, онда жаңа айнымалы енгізу арқылы шешуге болады: Жаңа айнымалы енгіземіз: t= t + = бастапқы теңдеулер жүйесіне ораламыз:
Слайд 8: Алгебралық қосу тәсілі
Теңдеулер жүйесіндегі бір айнымалыдан арылу үшін екі теңдеудегі айналылардың коэффиценттерін теңестіріп алып, мүшелеп қосу амалын орындаймыз: бірінші теңдеуді 3 ке, екіншіні 2 ге к өбейтеміз: Жауабы: (1 ; 2) ( - ; - )
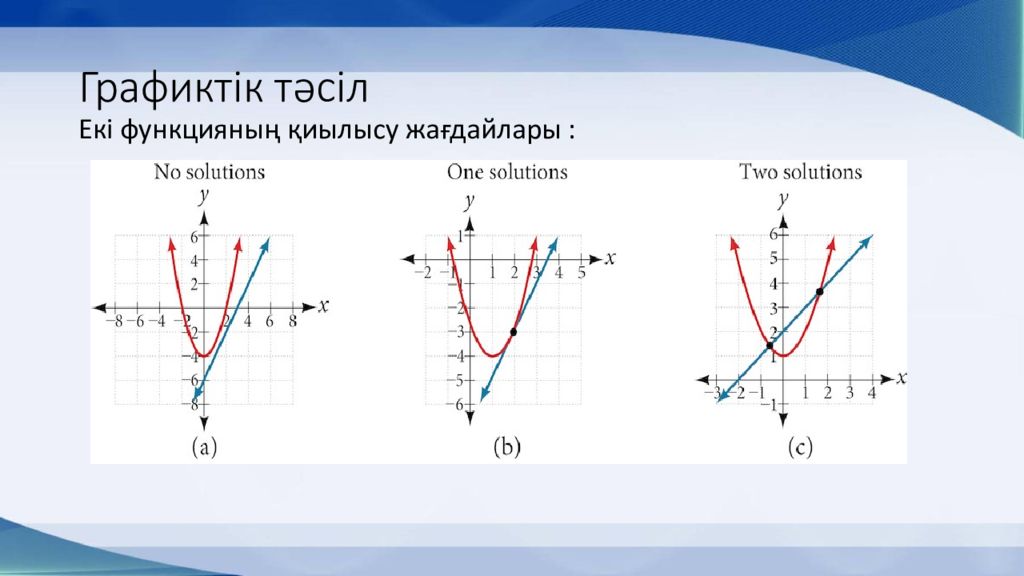
Слайд 9: Графиктік тәсіл
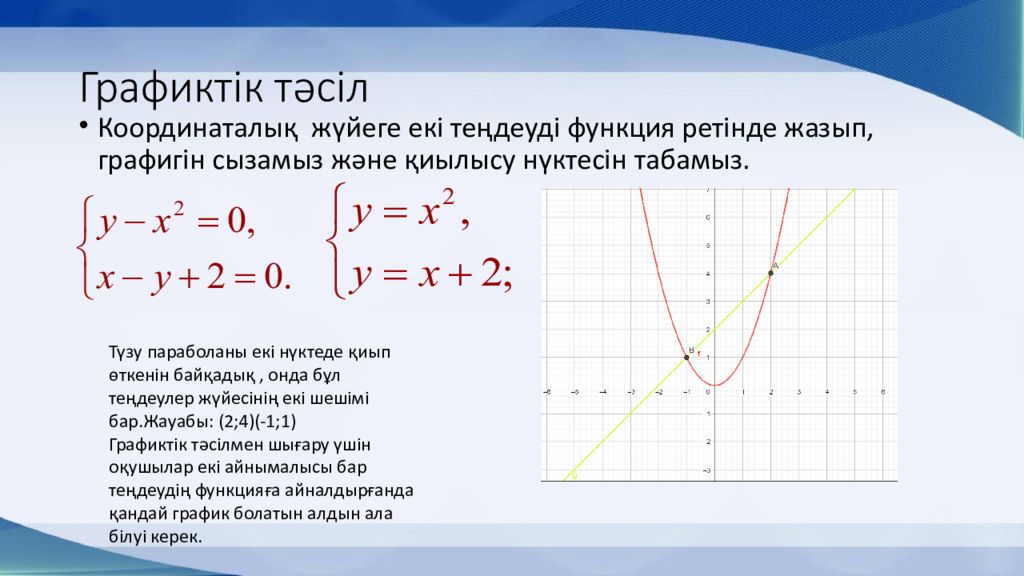
Координаталық жүйеге екі теңдеуді функция ретінде жазып, графигін сызамыз және қиылысу нүктесін табамыз. Түзу параболаны екі нүктеде қиып өткенін байқадық, онда бұл теңдеулер жүйесінің екі шешімі бар.Жауабы: (2 ; 4)(-1 ; 1) Графиктік тәсілмен шығару үшін оқушылар екі айнымалысы бар теңдеудің функцияға айналдырғанда қандай график болатын алдын ала білуі керек.
Слайд 11: Ортақ көбейткіштерін жақшаның сыртына шығару арқылы көбейткіштерге жіктеу
Жауабы: (3;4), (3; - 4), (0;5).
Слайд 12: Теңдеудің біртектілік қасиетін қолдану
Егер теңдеулер жүйесі осындай түрде берілсе, алгебралық қосу тәсілімен біртекті теңдеуге келтіріп, оны х – қа қатысты шешеміз.Бірінші теңдеуді (-3) ке, екінші теңдеуді 5 ке к өбейтіп, мүшелеп қосуды орындаймыз: = Жауабы:
Слайд 13: Виет теоремасын қолдану
Егер жүйе теңдеулердің бірі қосынды түрінде, ал екіншісі-кейбір квадрат теңдеудің түбірлері болып табылатын кейбір сандардың көбейтіндісі түрінде берілсе, онда Виет теоремасын қолдана отырып, біз квадрат теңдеуді құрамыз және оны шешеміз. - 5а + 4 = 0.