Схема независимых испытаний Бернулли Теория вероятностей
Повторение Теория вероятностей
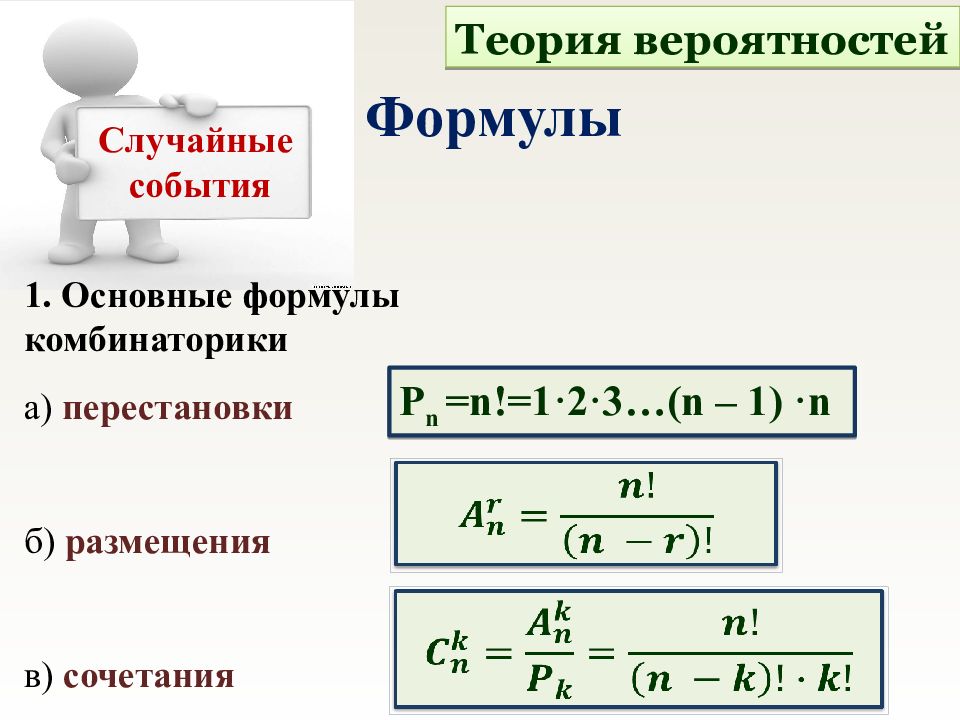
1. Основные формулы комбинаторики а) перестановки б) размещения в) сочетания P n =n!=1·2·3…(n – 1) ·n Теория вероятностей Формулы Случайные события
2. Классическое определение вероятности Теория вероятностей Формулы Случайные события , где m – число благоприятствующих событию A исходов, n – число всех элементарных равновозможных исходов
3. Вероятность суммы событий Теория вероятностей Формулы Случайные события Теорема сложения вероятностей несовместных событий: Теорема сложения вероятностей совместных событий: P(A+ B) = P(A) +P(B)−P(AB)
4. Вероятность произведения событий Теория вероятностей Формулы Случайные события Теорема умножения вероятностей независимых событий: Теорема умножения вероятностей зависимых событий: P(A⋅ B) = P(A) ⋅ P(B) P(A⋅ B) = P(A) ⋅ P(B|A) P(A⋅ B) = P(B) ⋅ P(A|B)
Сочетания Задача. Сколькими способам можно вывезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков ? Решение. n =10, r = 5, порядок не важен, повторений нет. Нужна формула: Сочетания
Размещения Задача. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин. Решение. n =11, r = 5, порядок важен (уроки идут по порядку), повторений нет. Нужна формула: Размещения
Перестановки Задача. Сколькими способами 4 человека могут разместиться в четырехместном купе? Решение. n = 4, r = 4, порядок важен (места в купе различны), нужно выбрать все объекты, повторений нет. Нужна формула: Перестановки P n = n!
Независимые испытания. Формула Бернулли При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний: 1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну; 2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой Независимые испытания. Формула Бернулли
Независимые испытания. Формула Бернулли А Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях).
Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли Распределение числа успехов (появлений события) носит название биномиального распределения. Независимые испытания. Формула Бернулли Сумма вероятностей всегда равна 1.
Формула Бернулли вероятность появления события ровно k раз при n независимых испытаниях, p - вероятность появления события при одном испытании.
Примеры: Пример 1. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых. Решение. Событие А – достали белый шар. Тогда вероятности, По формуле Бернулли требуемая вероятность равна
Примеры: Пример 2. Определить вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми. Решение. Вероятность рождения девочки, тогда Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки: Следовательно, искомая вероятность
Примеры: Пример 3. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными. Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - «появление нестандартной детали», его вероятность p = 0,004, тогда q = 0,96. Отсюда по формуле Бернулли находим
Примеры: Пример 4. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19. Решение. Вычисляем по формуле Бернулли:
Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов (появлений события) имеет вид: Так как то эти границы отличаются на 1. Поэтому k являющееся целым числом, может принимать либо одно значение, когда np целое число ( k=np ), то есть когда np+p ( а отсюда и np-q ) нецелое число, либо два значения, когда np-q целое число Наивероятнейшее число успехов
Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Найти наивероятнейшее число попаданий в цель. Решение n=25; p=0,7; q=0,3 Т.к. k - целое число, то k=18 Ответ: k=18
В урне 10 белых и 40 черных шаров. Подряд вынимают 14 шаров, причем цвет вынутого шара регистрируют, а затем шар возвращают в урну. Найти наивероятнейшее число появлений белого шара. Решение n=14; p=10 / 50=1 / 5; q=1-1 / 5=4 / 5 Т.о., задача имеет 2 решения: k=2; k=3 Ответ: k=2; k=3
7. В результате многолетних наблюдений установлено, что вероятность выпадения дождя в Москве 1 октября равна 1/7.Найти наивероятнейшее число дождливых дней в Москве 1 октября за 40 лет. 8. Имеется 20 ящиков однородных деталей. Вероятность того, что в одном наудачу взятом ящике детали окажутся стандартными, равна 0,75. Найти наивероятнейшее число ящиков, в которых все детали стандартные. 9. В урне 100 белых и 80 черных шаров. Из урны извлекают n шаров (с возвратом каждого вынутого шара).Наивероятнейшее число появлений белого шара равно 11. Найти n.
10. Один рабочий за смену может изготовить 120 изделий, другой – 140 изделий, причем вероятности того, что эти изделия высшего сорта, составляют соответственно 0,94 и 0,8. Определить наивероятнейшее число изделий высшего сорта, изготовленных каждым рабочим.
1. В каждом из 4 ящиков по 5 белых и по 15 черных шаров. Из каждого ящика вынули по одному шару. Какова вероятность вынуть 2 белых и 2 черных шара? 2. Имеется 100 урн с белыми и черными шарами. Вероятность появления белого шара из каждой урны равно 0,6. Найти наивероятнейшее число урн, в которых все шары белые.
