Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше. Указанные события противоположны, поэтому искомая вероятность равна 1 − 0,81 = 0,19.
При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм. По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035.
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
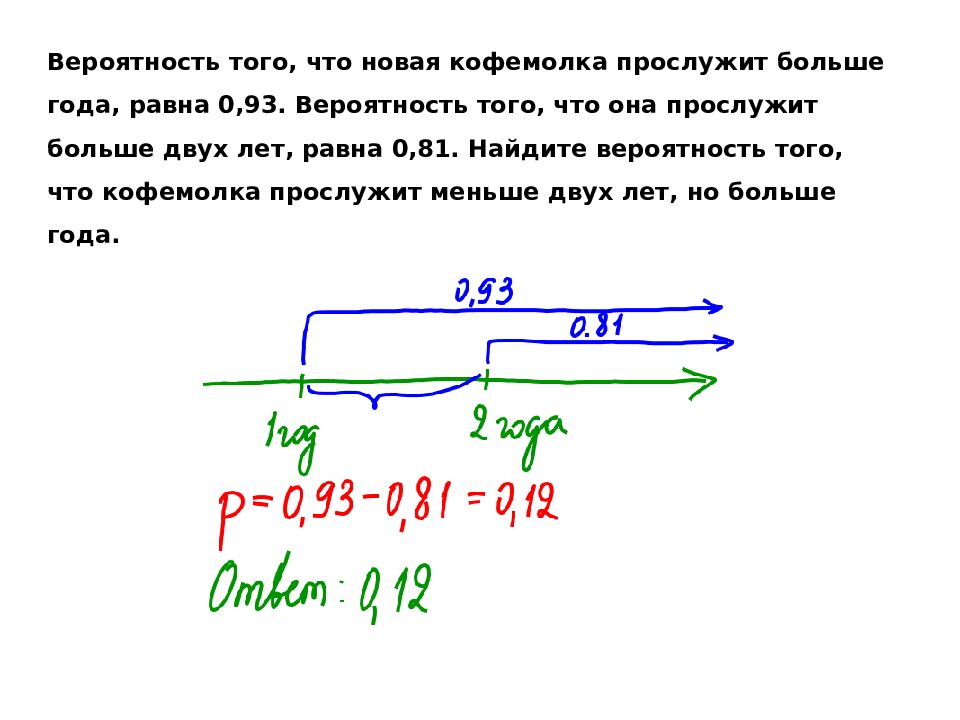
Вероятность того, что новая кофемолка прослужит больше года, равна 0,93. Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года.
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года. Решение. Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года». События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час, наносекунду и т. д. — равна нулю. Тогда: P(A + B + С) = P(A) + P(B) + P(С)= P(A) + P(B), откуда, используя данные из условия, получаем 0,97 = P(A) + 0,89. Тем самым для искомой вероятности имеем: P(A) = 0,97 − 0,89 = 0,08. Ответ: 0,08.
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17. Рассмотрим события A = «в автобусе меньше 10 пассажиров» и В = «в автобусе от 10 до 17 пассажиров». Их сумма — событие A + B = «в автобусе меньше 18 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,82 = 0,51 + P(В), откуда P(В) = 0,82 − 0,51 = 0,31. Ответ: 0,31.
Вероятность того, что на тестировании по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач. Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по теме «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. ПРАВИЛО «ИЛИ» Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий
