Первый слайд презентации: Содержание:
Графы: определения и примеры Ориентированные графы Путь в орграфе Матрица смежности Иерархический список Алгоритм Дейкстры Программа “ ProGraph ” Описание работы программы Достоинства программы Список литературы
Слайд 2: Графы: определения и примеры
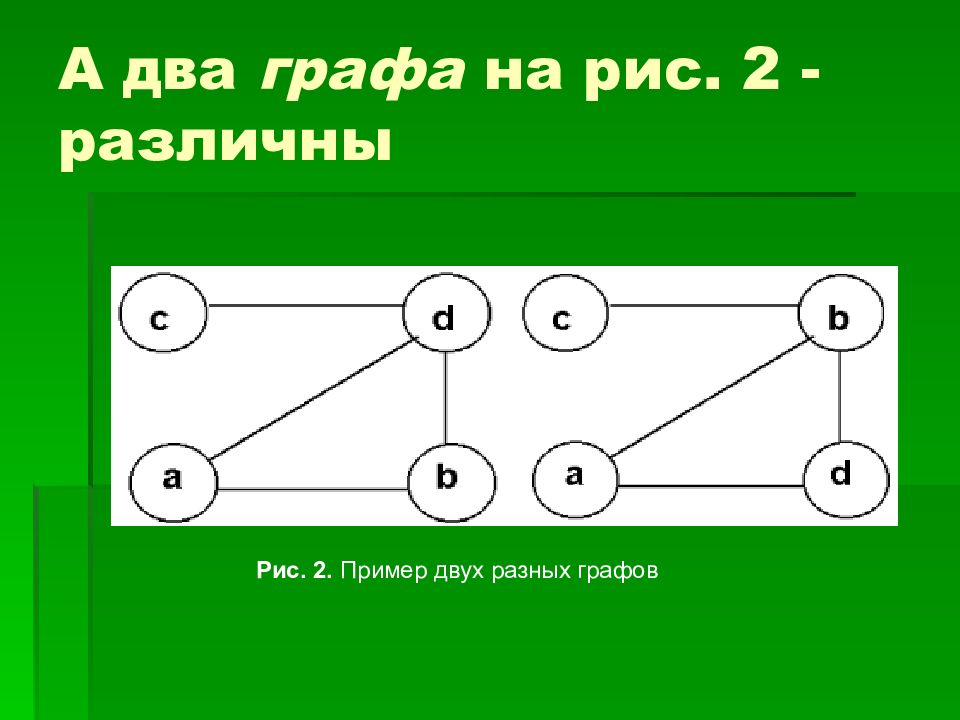
Говоря простым языком, граф - это множество точек (для удобства изображения - на плоскости) и попарно соединяющих их линий (не обязательно прямых). В графе важен только факт наличия связи между двумя вершинами. От способа изображения этой связи структура графа не зависит.
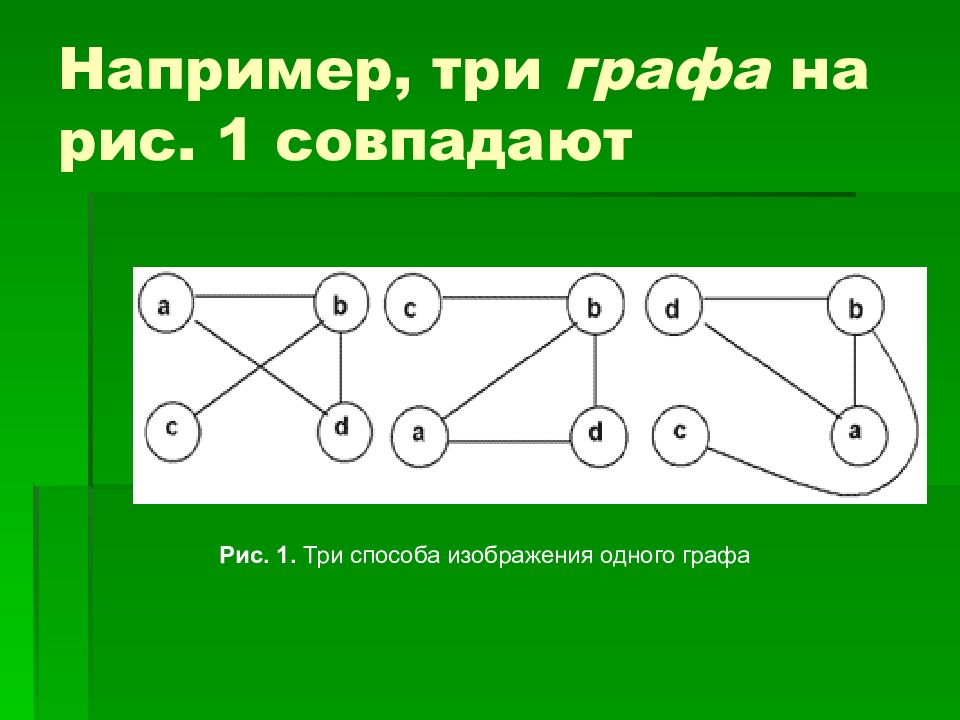
Слайд 3: Например, три графа на рис. 1 совпадают
Рис. 1. Три способа изображения одного графа Например, три графа на рис. 1 совпадают
Слайд 5: Степень вершины
Любому ребру соответствует ровно две вершины, а вот вершине может соответствовать произвольное количество ребер, это количество и определяет степень вершины. Изолированная вершина вообще не имеет ребер (ее степень равна 0).
Слайд 6: Смежные вершины и рёбра
Две вершины называются смежными, если они являются разными концами одного ребра. Два ребра называются смежными, если они выходят из одной вершины.
Слайд 7: Путь в графе
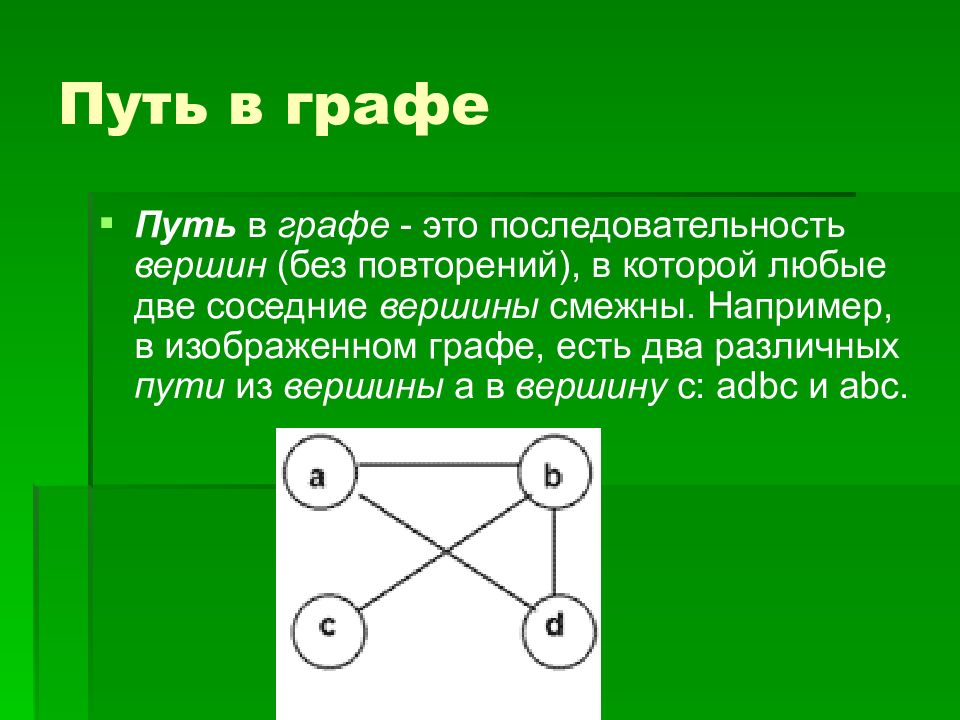
Путь в графе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны. Например, в изображенном графе, есть два различных пути из вершины a в вершину с: adbc и abc.
Слайд 8: Достижимость
Вершина v достижима из вершины u, если существует путь, начинающийся в u и заканчивающийся в v. Граф называется связным, если все его вершины взаимно достижимы.
Слайд 9: Длина пути
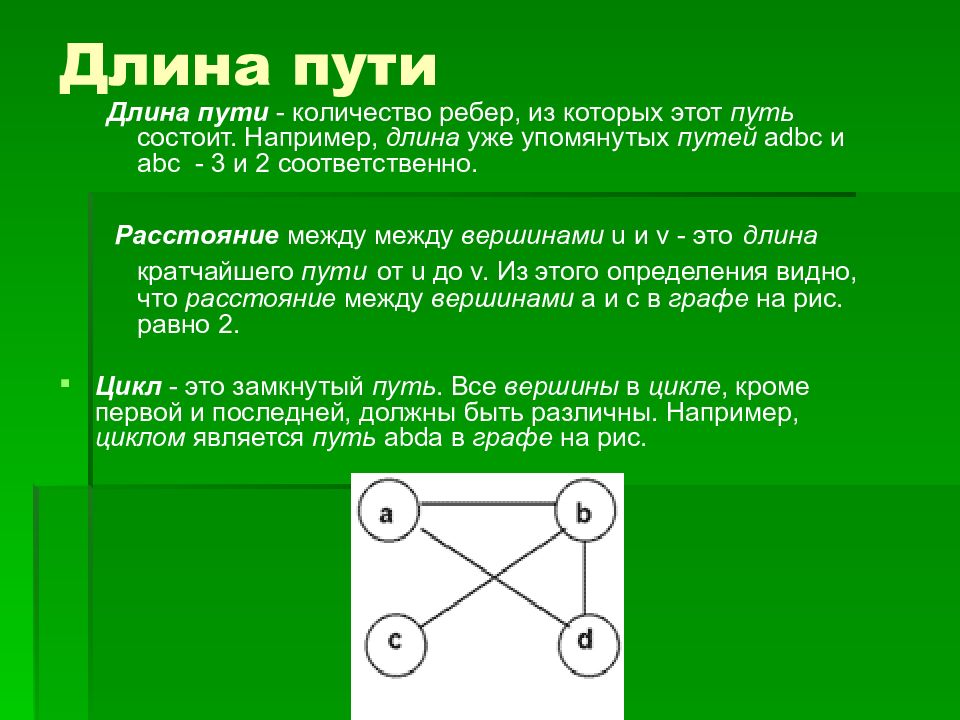
Длина пути - количество ребер, из которых этот путь состоит. Например, длина уже упомянутых путей adbc и abc - 3 и 2 соответственно. Расстояние между между вершинами u и v - это длина кратчайшего пути от u до v. Из этого определения видно, что расстояние между вершинами a и c в графе на рис. равно 2. Цикл - это замкнутый путь. Все вершины в цикле, кроме первой и последней, должны быть различны. Например, циклом является путь abda в графе на рис.
Слайд 10: Примеры неориентированных графов
Граф Вершины Ребра Семья Люди Родственные связи Город Перекрестки Улицы Сеть Компьютеры Кабели Домино Костяшки Возможность Дом Квартиры Соседство Лабиринт Развилки и тупики Переходы Метро Станции Пересадки Листок в клеточку Клеточки Наличие общей границы
Слайд 11: Ориентированные графы
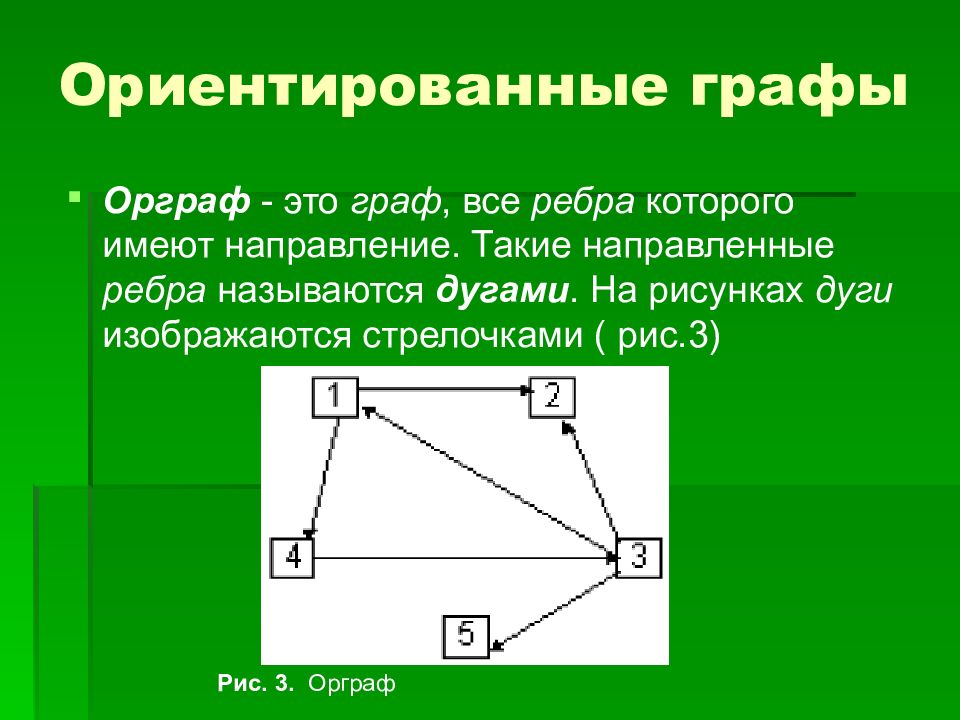
Орграф - это граф, все ребра которого имеют направление. Такие направленные ребра называются дугами. На рисунках дуги изображаются стрелочками ( рис.3) Рис. 3. Орграф
Слайд 12: Смешанный граф
В отличие от ребер, дуги соединяют две неравноправные вершины : одна из них называется началом дуги ( дуга из нее исходит ), вторая - концом дуги ( дуга в нее входит ). Можно сказать, что любое ребро - это пара дуг, направленных навстречу друг другу. Если в графе присутствуют и ребра, и дуги, то его называют смешанным
Слайд 13: Путь в орграфе
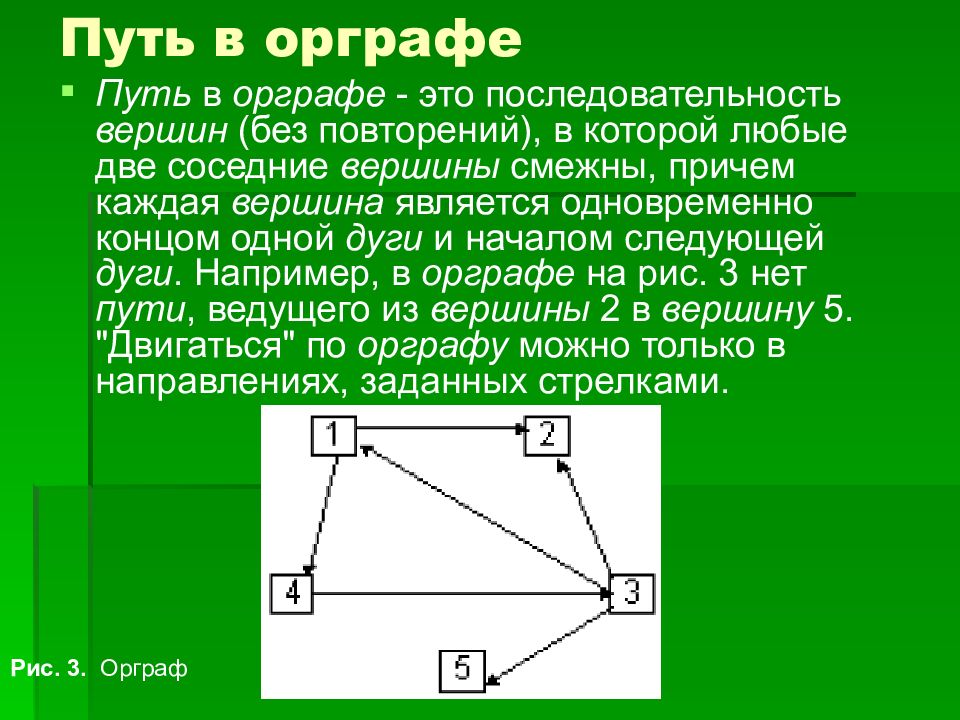
Путь в орграфе - это последовательность вершин (без повторений), в которой любые две соседние вершины смежны, причем каждая вершина является одновременно концом одной дуги и началом следующей дуги. Например, в орграфе на рис. 3 нет пути, ведущего из вершины 2 в вершину 5. "Двигаться" по орграфу можно только в направлениях, заданных стрелками. Рис. 3. Орграф
Слайд 14: Примеры ориентированных графов
Орграф Вершины Дуги Чайнворд Слова Совпадение последней и первой букв (возможность связать два слова в цепочку) Стройка Работы Необходимое предшествование (например, стены нужно построить раньше, чем крышу, т. п.) Обучение Курсы Необходимое предшествование (например, курс по языку Pascal полезно изучить прежде, чем курс по Delphi, и т.п.) Одевание ребенка Предметы гардероба Необходимое предшествование (например, носки должны быть надеты раньше, чем ботинки, и т.п.) Европейский город Перекресток Узкие улицы с односторонним движением
Слайд 15: Взвешенные графы
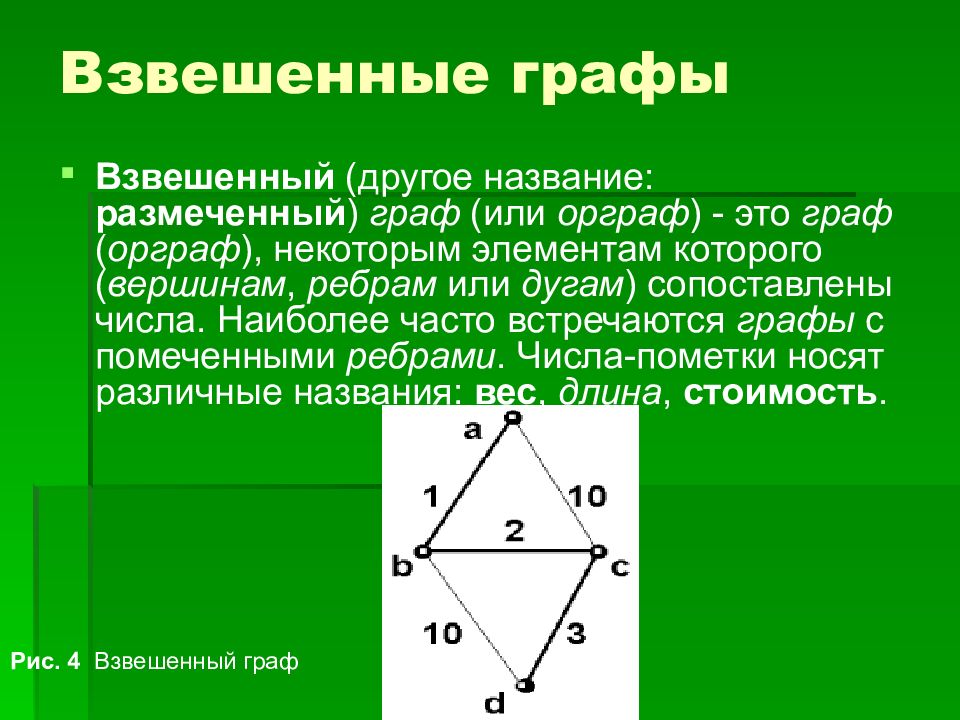
Взвешенный (другое название: размеченный ) граф (или орграф ) - это граф ( орграф ), некоторым элементам которого ( вершинам, ребрам или дугам ) сопоставлены числа. Наиболее часто встречаются графы с помеченными ребрами. Числа-пометки носят различные названия: вес, длина, стоимость. Рис. 4 Взвешенный граф
Слайд 16: Длина пути во взвешенном графе
Длина пути во взвешенном (связном) графе - это сумма длин (весов) тех ребер, из которых состоит путь. Расстояние между вершинами - это, как и прежде, длина кратчайшего пути. Например, расстояние от вершины a до вершины d во взвешенном графе, изображенном на рис. 4, равно 6. Рис. 4 Взвешенный граф
Слайд 17: Примеры взвешенных графов
Граф Вершины Вес вершины Ребра (дуги) Вес ребра (дуги) Таможни Государства Площадь территории Наличие наземной границы Стоимость получения визы Переезды Города Стоимость ночевки в гостинице Дороги Длина дороги Супер-чайнворд Слова - Совпадение конца и начала слов(возможность "сцепить" слова) Длина пересекающихся частей Карта Государства Цвет на карте Наличие общей границы - Сеть Компьютеры - Сетевой кабель Стоимость кабеля
Слайд 18: Способы представления графов
Существует довольно большое число разнообразных способов представления графов. Однако мы изложим здесь только самые полезные с точки зрения программирования.
Слайд 19: Матрица смежности
Матрица смежности Sm - это квадратная матрица размером N x N (N - количество вершин в графе ), заполненная по следующему правилу: Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = V es(e), в противном случае Sm[u,v] = “-”.
Слайд 20: Пример матрицы смежности
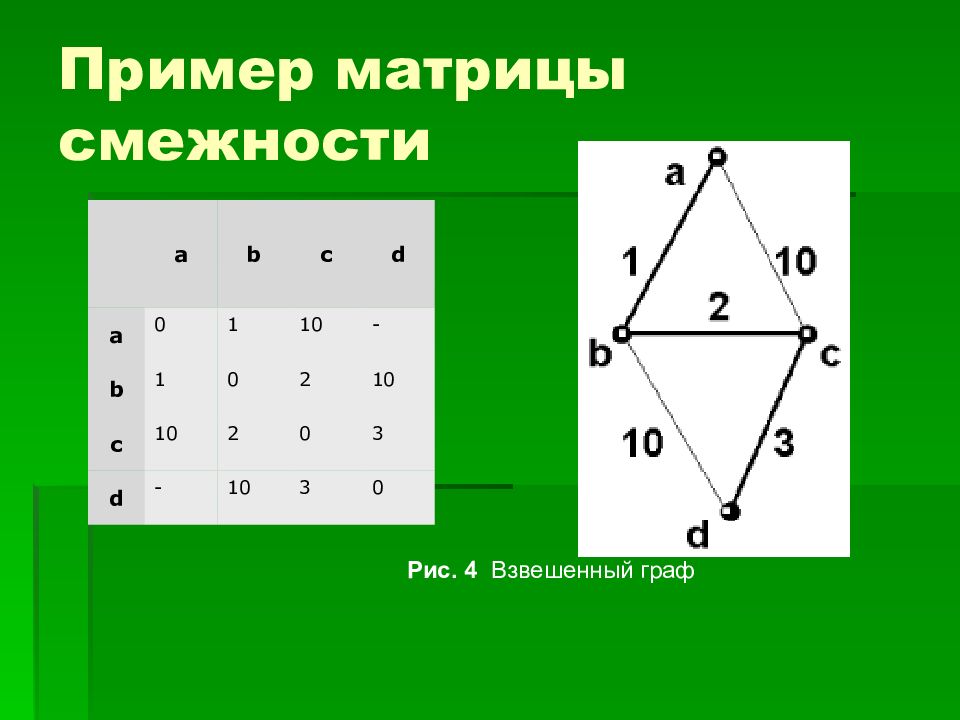
a b c d a 0 1 10 - b 1 0 2 10 c 10 2 0 3 d - 10 3 0 Рис. 4 Взвешенный граф
Слайд 21: Преимущества матрицы смежности
Удобство матрицы смежности состоит в наглядности и прозрачности алгоритмов, основанных на ее использовании. А неудобство - в несколько завышенном требовании к памяти: если граф далек от полного, то в массиве, хранящем матрицу смежности, оказывается много "пустых мест" (нулей). Кроме того, для "общения" с пользователем этот способ представления графов не слишком удобен: его лучше применять только для внутреннего представления данных.
Слайд 22: Иерархический список
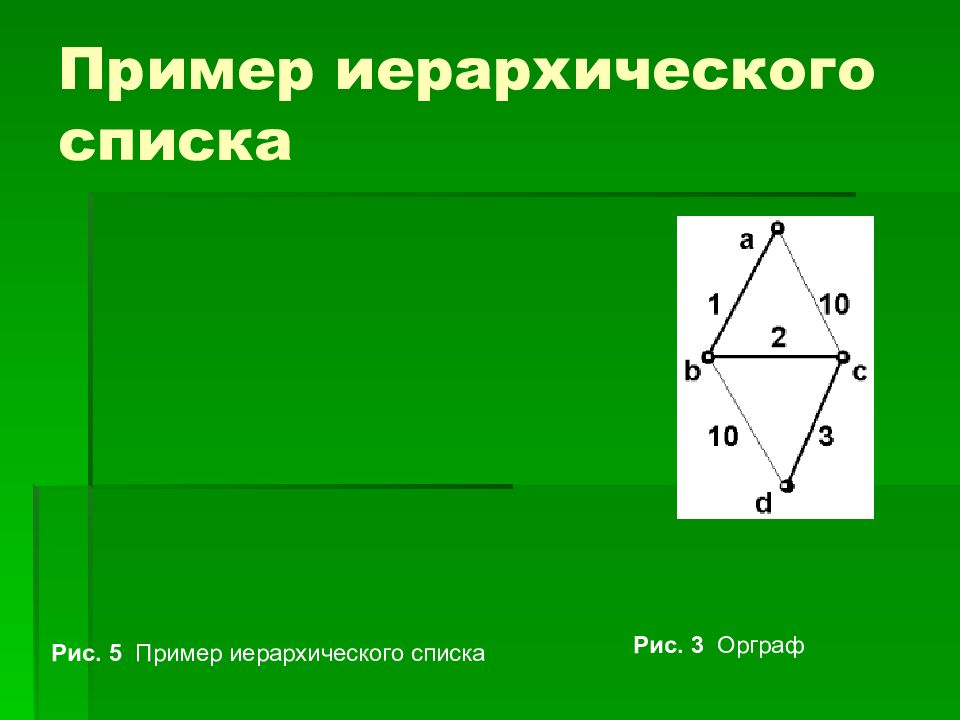
В одном линейном списке содержатся номера "начальных вершин ", а в остальных - номера смежных вершин или указатели на эти вершины. В качестве примера приведем иерархический список, задающий орграф, изображенный на рис.3
Слайд 23: Пример иерархического списка
Рис. 5 Пример иерархического списка Рис. 3 Орграф
Слайд 24: Преимущества иерархического списка
Вершина = запись Номер : Число ; Имя: Строка; След Вершина: указатель на Вершина ; Список Дуг: Дуга ; end; Дуга = запись Стоимость: Число; Конец Дуги: Вершина; След Дуга: Дуга ; end; Очевидное преимущество такого способа представления графов заключается в экономичном использовании памяти. И даже небольшая избыточность данных, к которой приходится прибегать в случае неориентированного графа, задавая каждое ребро как две дуги, искупается гибкостью всей структуры, что особенно удобно при необходимости частых перестроений в процессе работы программы.
Слайд 25: Программа “ProGraph”
Программа “ProGraph” была специально созданна для создания графов в графической оболочке. Поддерживает возможность добавления алгоритмов на графах.
Слайд 26: Алгоритм Дейкстры
Мы рассмотрим один из основных алгоритмов поиска кратчайших путей в графе – алгоритм Дейкстры, применимый для графов с неотрицательными весами.
Слайд 27: Описание алгоритма
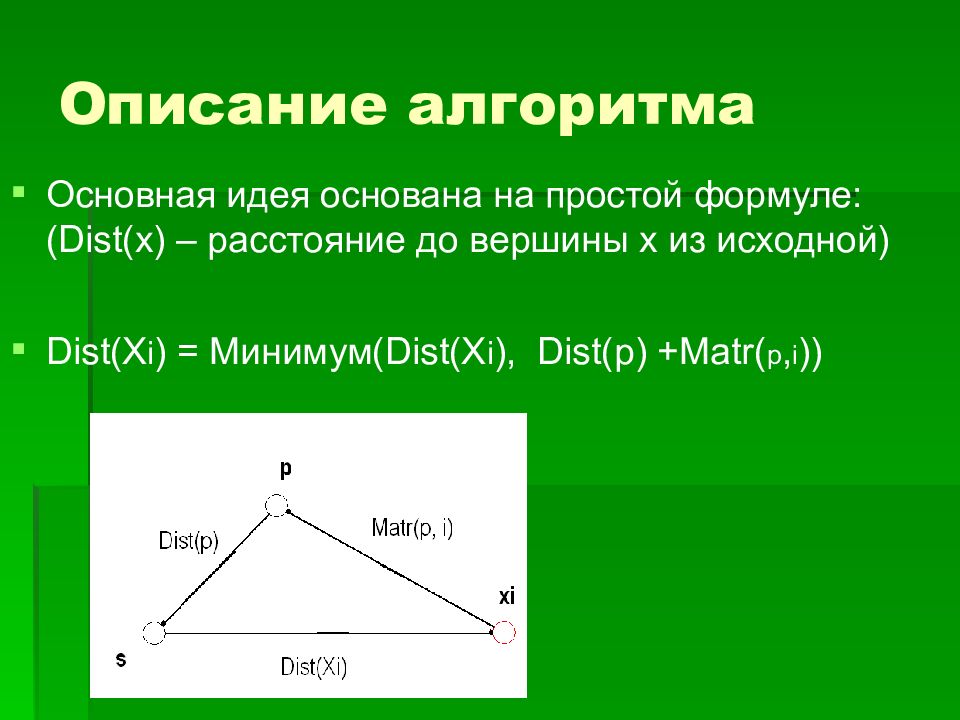
Основная идея основана на простой формуле: (Dist ( x) – расстояние до вершины x из исходной) Dist ( X i ) = Минимум (Dist ( X i ), Dist(p) +Matr( p, i ) )
Слайд 28: Описание алгоритма
Допустим, нам надо найти кратчайший путь из вершины A в вершину D. Перебираем все возможные расстояния до вершин, находим из них минимальное и выводим кратчайший путь. a b c d a 0 1 10 - b 1 0 2 10 c 10 2 0 3 d - 10 3 0
Слайд 29
Описание работы программы Работа делится на две части: Создание графа в Редакторе. Применение алгоритма Дейкстры к получившемуся графу и просмотр результата.
Слайд 30
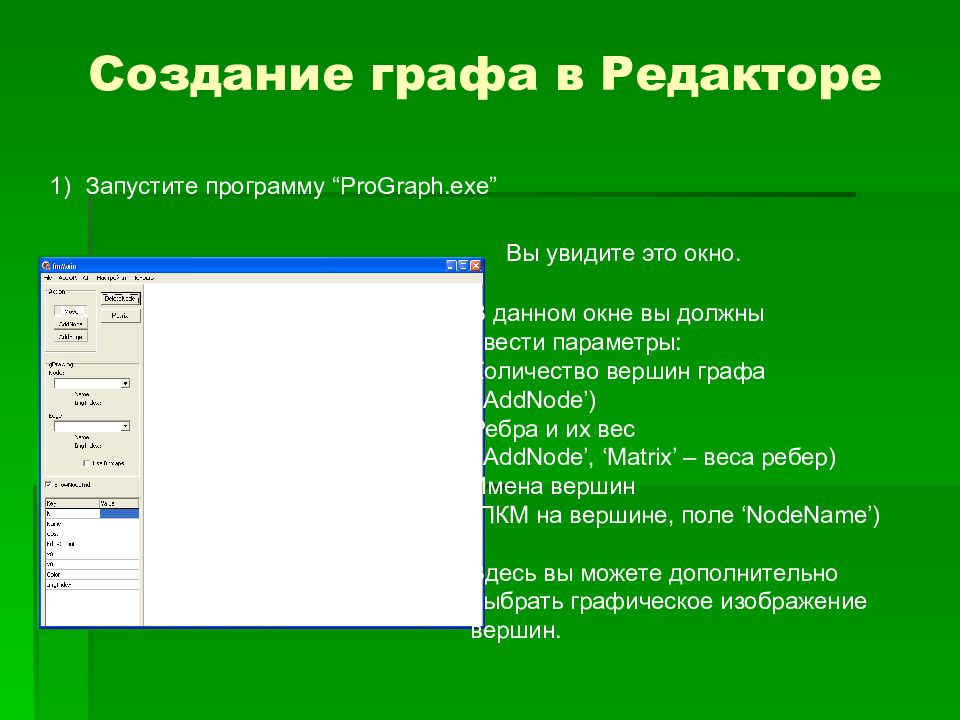
Создание графа в Редакторе Запустите программу “ProGraph.exe” Вы увидите это окно. В данном окне вы должны ввести параметры: Количество вершин графа ( ‘ AddNode ’ ) Ребра и их вес ( ‘ AddNode ’, ‘Matrix’ – веса ребер) Имена вершин (ПКМ на вершине, поле ‘ NodeName ’) Здесь вы можете дополнительно выбрать графическое изображение вершин.
Слайд 31
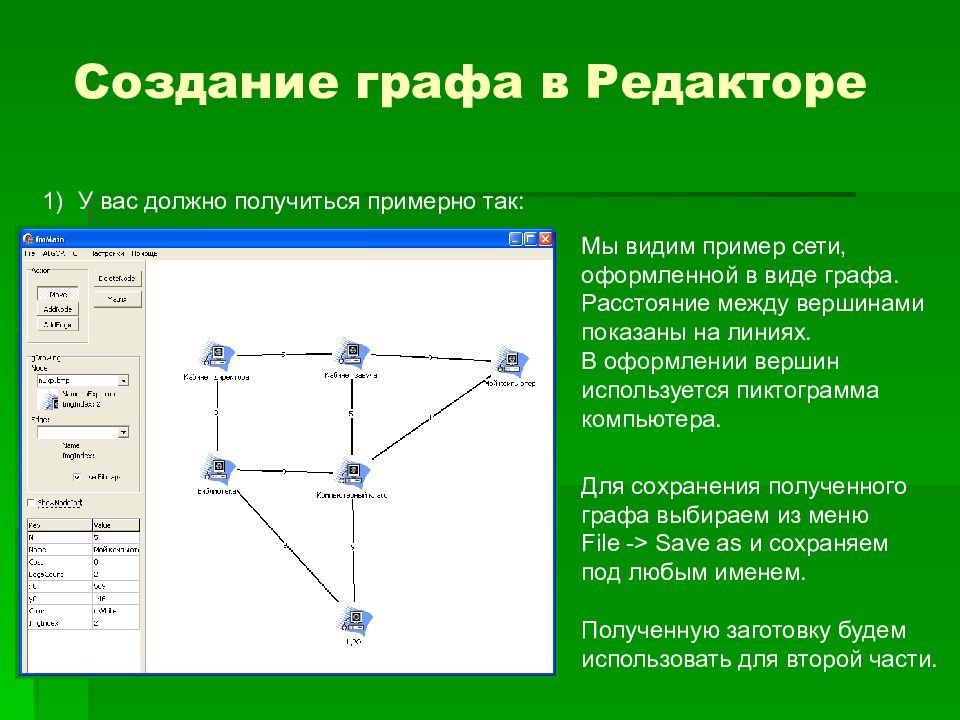
Создание графа в Редакторе У вас должно получиться примерно так: Мы видим пример сети, оформленной в виде графа. Расстояние между вершинами показаны на линиях. В оформлении вершин используется пиктограмма компьютера. Для сохранения полученного графа выбираем из меню File -> Save as и сохраняем под любым именем. Полученную заготовку будем использовать для второй части.
Слайд 32
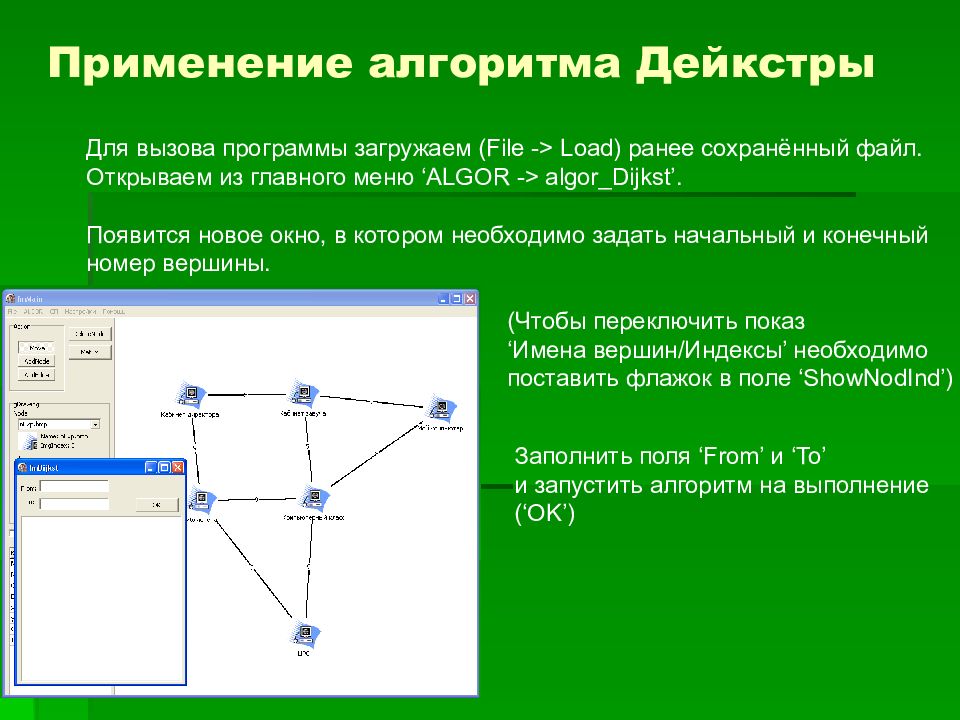
Применение алгоритма Дейкстры Для вызова программы загружаем ( File -> Load) ранее сохранённый файл. Открываем из главного меню ‘ALGOR -> algor_Dijkst’. Появится новое окно, в котором необходимо задать начальный и конечный номер вершины. (Чтобы переключить показ ‘ Имена вершин/Индексы ’ необходимо поставить флажок в поле ‘ShowNodInd’ ) Заполнить поля ‘From’ и ‘To’ и запустить алгоритм на выполнение ( ‘OK’)
Слайд 33
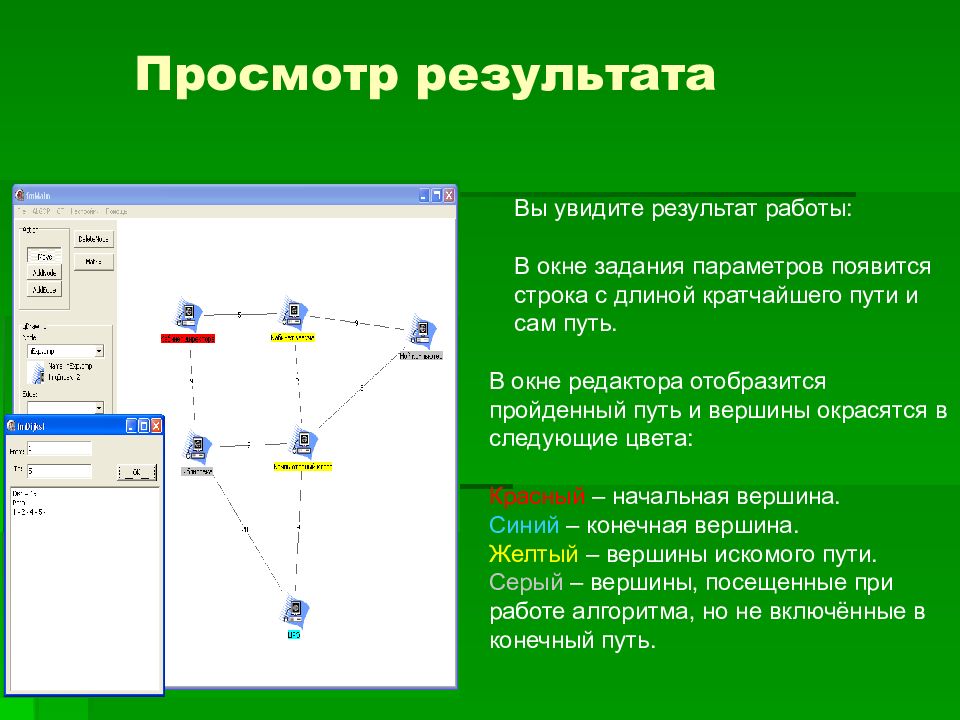
Просмотр результата Вы увидите результат работы: В окне задания параметров появится строка с длиной кратчайшего пути и сам путь. В окне редактора отобразится пройденный путь и вершины окрасятся в следующие цвета: Красный – начальная вершина. Синий – конечная вершина. Желтый – вершины искомого пути. Серый – вершины, посещенные при работе алгоритма, но не включённые в конечный путь.
Слайд 34
Достоинства программы С помощью этой программы вы можете создать любой граф с помощью удобного редактора графов: схема метро, карта городов, компьютерные сети, карту лабиринта и многое другое. Представить его в графическом виде, добавляя названия вершин, пиктограммы, расстояния. Определить кратчайший путь между двумя заданными вершинами и увидеть результат работы алгоритма в графическом и текстовом виде. Программа была создана на языке “Delphi” с использованием объектно-ориентированного программирования. Данная программа может быть использована для подготовки к ЕГЭ по информатике.
Последний слайд презентации: Содержание:
Кирюхин В.М., Лапунов А.В., Окулов С.М. Задачи по информатике: Международные олимпиады 1989 – 1996: Для факультативов по информатике в старших классах. – М.: ABF, 1996 Боглаев Ю.П. Вычислительная математика и программирование. – М.: Высшая школа, 1990 Кушниренко А.Г., Лебедев Г.В. Программирование для математиков. – М.: Наука, 1988. Майерс Г. Искусство тестирования программ. – М.: Финансы и статистика, 1982. Никольская И.Л. Математическая логика. – M. : Высшая школа, 1981. Список использованной литературы