Первый слайд презентации
Связанные колебательные контуры В радиотехнике широко применяется способ выделения полезных сигналов с помощью частотно-избирательных линейных цепей. Такие цепи пропускают лишь колебания с частотами, которые лежат в относительно узкой полосе вокруг некоторой центральной частоты. Простейшей узкополосной частотно-избирательной системой является колебательный контур. В радиотехнике такие контуры применяются в основном как фильтры промежуточной частоты (ФПЧ). Однако одноконтурные узкополосные цепи обладают существенным недостатком — невысокой частотной избирательностью. За границами полосы пропускания значения амплитудно-частотные характеристики (АЧХ) таких цепей стремятся к нулю недостаточно быстро. Поэтому выходное колебание содержит не только полезный сигнал, спектр которого располагается вблизи максимума АЧХ, но и некоторую, порой значительную долю мешающих сигналов, шумов и т. д. Для повышения частотной избирательности фильтров используют многоконтурные устройства, в которых удается получить форму АЧХ, близкую к идеальной (прямоугольной). Простейшим многоконтурным частотно-избирательным фильтром является система двух связанных колебательных контуров. Контуры называются связанными, если имеет место переход энергии из одного контура в другой.
Слайд 2
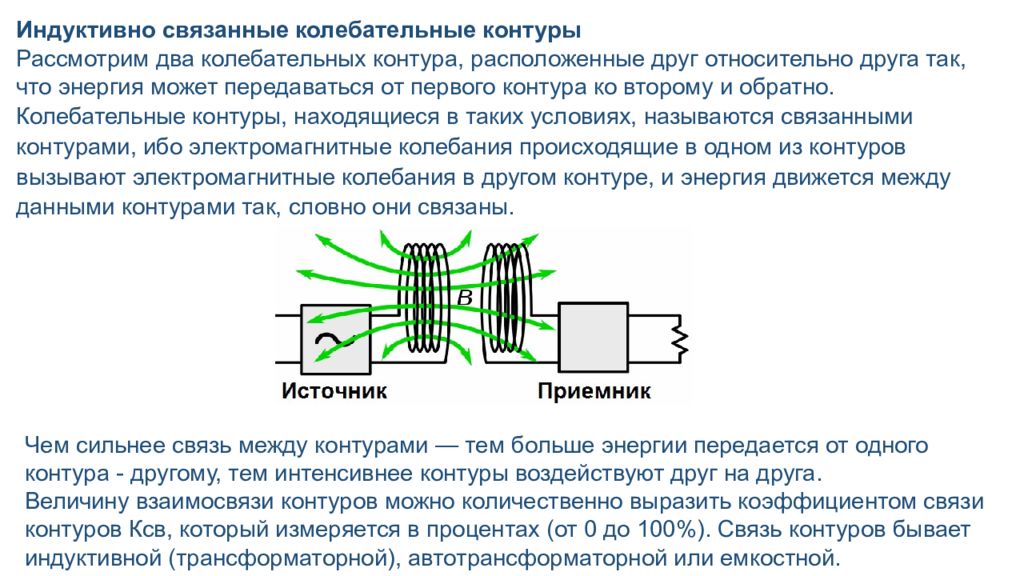
Индуктивно связанные колебательные контуры Рассмотрим два колебательных контура, расположенные друг относительно друга так, что энергия может передаваться от первого контура ко второму и обратно. Колебательные контуры, находящиеся в таких условиях, называются связанными контурами, ибо электромагнитные колебания происходящие в одном из контуров вызывают электромагнитные колебания в другом контуре, и энергия движется между данными контурами так, словно они связаны. Чем сильнее связь между контурами — тем больше энергии передается от одного контура - другому, тем интенсивнее контуры воздействуют друг на друга. Величину взаимосвязи контуров можно количественно выразить коэффициентом связи контуров Ксв, который измеряется в процентах (от 0 до 100%). Связь контуров бывает индуктивной (трансформаторной), автотрансформаторной или емкостной.
Слайд 3
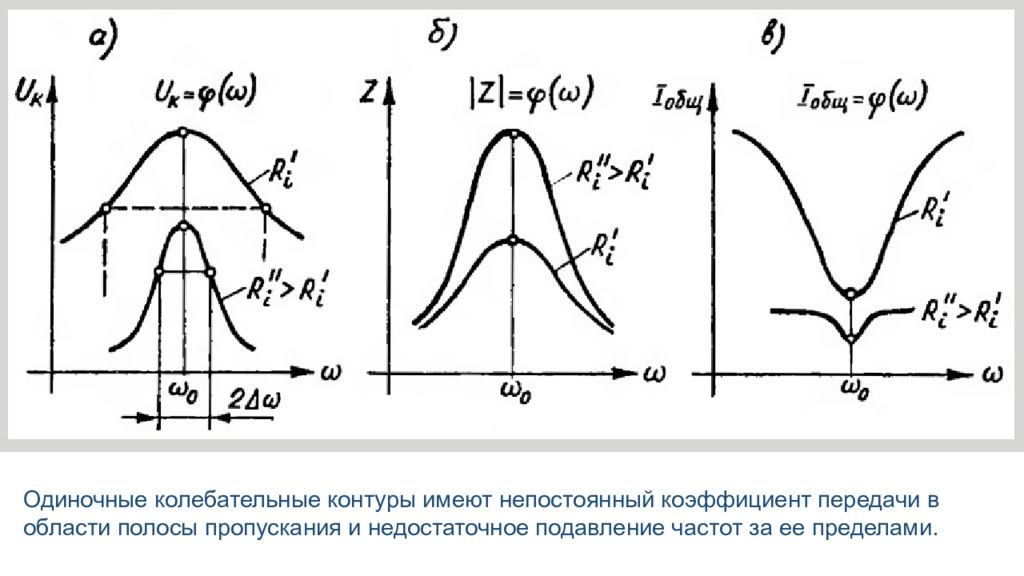
Одиночные колебательные контуры имеют непостоянный коэффициент передачи в области полосы пропускания и недостаточное подавление частот за ее пределами.
Слайд 4
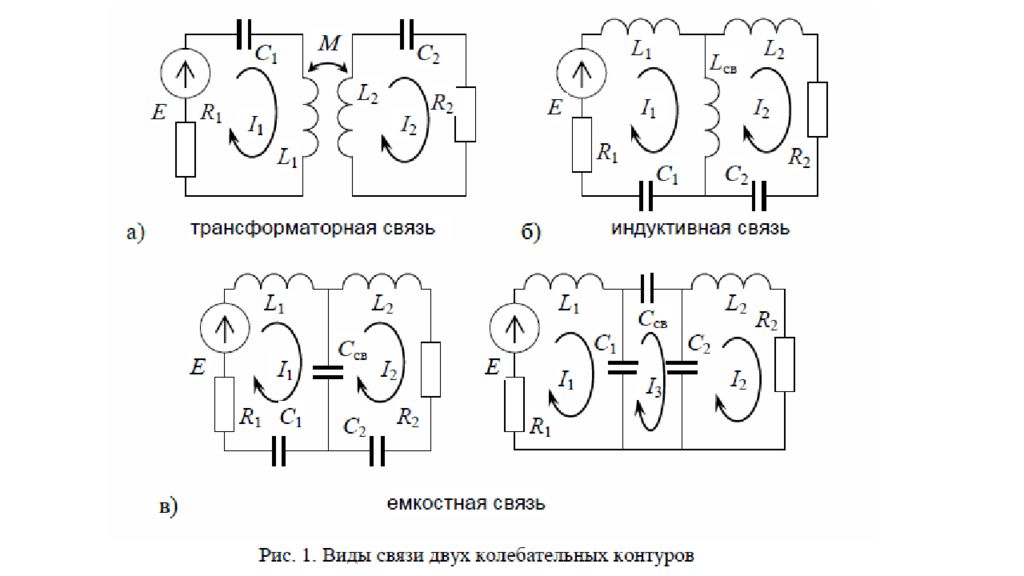
Связь между контурами при заданной полосе пропускания можно подобрать такой, чтобы резонансная кривая системы была по форме близка к П-образной характеристике идеального полосового фильтра. Подобную систему широко используют в основном для усиления промежуточной частоты радиоприемников. Кроме двухконтурных, в радиоаппаратуре находят применение и многоконтурные связанные системы. Их АЧХ еще более приближаются к П-образной форме. В настоящее время вместо колебательных контуров используют фильтры промежуточной частоты (ПЧ) на пьезоэффекте. Связь между контурами может осуществляться через электрическое поле (благодаря емкости) или через магнитное поле (благодаря взаимоиндуктивности или индуктивности). На рис. 1 показаны три разновидности связи двух колебательных контуров: а ) трансформаторная, когда связь между контурами осуществляется благодаря взаимоиндуктивности между катушками L 1 и L 2; б ) индуктивная, когда связь между контурами осуществляется непосредственно через индуктивность связи L 1,2; в ) емкостная, когда связь между контурами осуществляется через емкость связи С 3. Наиболее часто в радиотехнике применяется трансформаторная связь.
Слайд 6
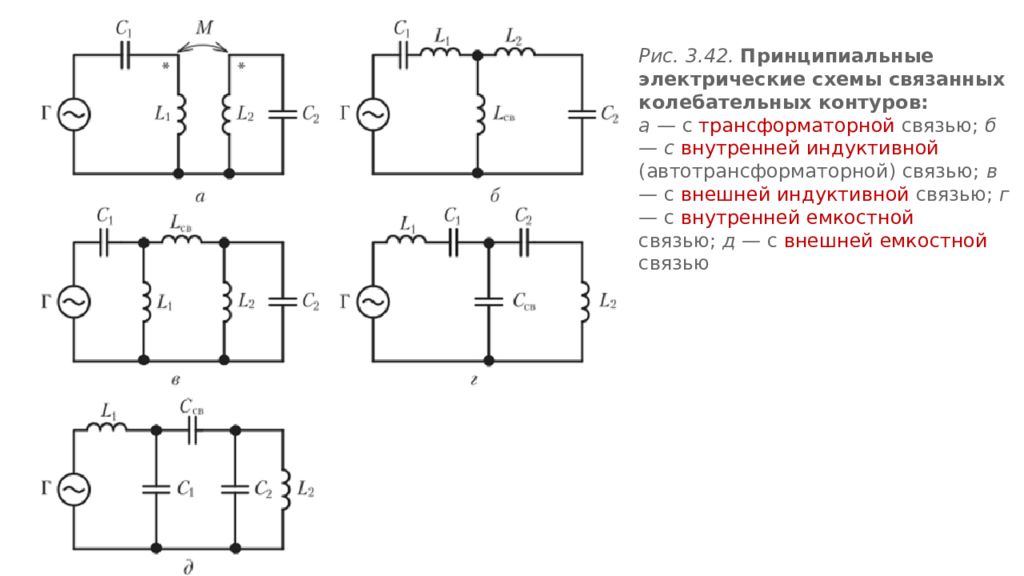
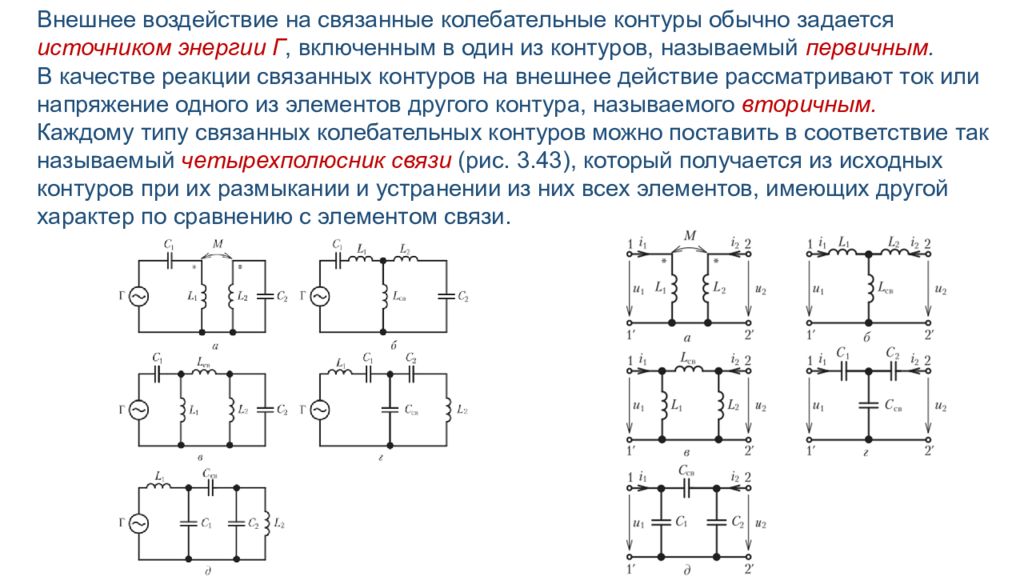
Рис. 3.42. Принципиальные электрические схемы связанных колебательных контуров: а — с трансформаторной связью; б — с внутренней индуктивной (автотрансформаторной) связью; в — с внешней индуктивной связью; г — с внутренней емкостной связью; д — с внешней емкостной связью
Слайд 7
Внешнее воздействие на связанные колебательные контуры обычно задается источником энергии Г, включенным в один из контуров, называемый первичным. В качестве реакции связанных контуров на внешнее действие рассматривают ток или напряжение одного из элементов другого контура, называемого вторичным. Каждому типу связанных колебательных контуров можно поставить в соответствие так называемый четырехполюсник связи (рис. 3.43), который получается из исходных контуров при их размыкании и устранении из них всех элементов, имеющих другой характер по сравнению с элементом связи.
Слайд 8
В системе из двух связанных контуров, имеющих одинаковые собственные частоты , во вторичном контуре наводится э.д.с. Связь между контурами характеризуется коэффициентом связи. Вторичный контур, в котором возникают вынужденные колебания, в свою очередь оказывает обратное воздействие на контур первичный, изменяя его параметры и внося в него добавочное сопротивление. Одиночные колебательные контуры имеют непостоянный коэффициент передачи в области полосы пропускания и недостаточное подавление частот за ее пределами. Эти недостатки в значительно меньшей степени присущи связанным колебательным контурам. Система связанных контуров позволяет уменьшить влияние внутреннего сопротивления источника сигнала и нагрузки на контур и получать резонансные кривые, близкие к П-образным или специальной формы.
Слайд 9
Рис. 104. Схема связанных контуров : а —- индуктивная связь; б —автотрансформатор- ная связь; в — емкостная связь. Простейшей и, вместе с тем, наиболее распространенной является индуктивная (трансформаторная) связь между контурами ( рис. 104, а ). Э.д.с. Е, подключенная к первому контуру, создает в нем ток I 1. Около катушки индуктивности L 1 образуется переменное магнитное поле, которое наводит в катушке L 2 э.д.с. взаимоиндукции. Во втором контуре появляется ток I 2, создающий около катушки L 2 переменное магнитное поле, которое, в свою очередь, наводит э. д. с. взаимоиндукции в первом контуре. Так как катушки L 1 и L 2 находятся на некотором расстоянии друг от друга, то часть магнитных силовых линий катушки L 1 замыкается в окружающем пространстве, не достигая катушки L 2. Степень влияния контуров друг на друга оценивается коэффициентом связи К св. В случае индуктивной связи между контурами он показывает, во сколько раз э.д.с, наводимая во втором контуре, меньше той э.д.с, которая могла бы быть в нем наведена, если бы все магнитные силовые линии катушки L 1 участвовали в ее создании.
Слайд 10
Таким образом, коэффициент связи всегда меньше единицы: Изменяя расстояние между катушками, можно менять величину коэффициента К св. В ряде случаев это изменение связи между контурами осуществляют, поворачивая одну катушку относительно другой, при фиксированном расстоянии между катушками. При индуктивной связи Формула примет более общий вид, если числитель и знаменатель умножить на ω: Итак, коэффициент связи между контурами определяется отношением сопротивления связи ( Х св ) к корню квадратному из произведения одноименных реактивных сопротивлений контура (индуктивных или емкостных). Коэффициент взаимной индукции двух контуров (М ) равен магнитному потоку, сцепленному с одним из контуров, когда ток в другом контуре равен единице. Взаимная индуктивность зависит от геометрической формы, размеров, взаимного расположения контуров и от магнитных свойств среды, окружающей их.
Слайд 11
В этом случае сопротивление связи Х св = ωL 1,2, одноименные реактивные сопротивления контуров Х 1 и Х 2 соответственно равны ( L 1 + L 1,2 ) и ( L 2 + L 1,2 ). Подставив значения Х св, X 1 и Х 2 в формулу, после несложных преобразований получим, применительно к рассматриваемому случаю автотрансформаторной связи, выражение для коэффициента связи : Как следует из формулы, связь между контурами тем больше, чем больше индуктивность L 1,2. На рис. 104, б показана система связанных контуров при так называемой автотрансформаторной связи между контурами, когда взаимное влияние контуров друг на друга осуществляется через катушку индуктивности L 1,2, одновременно входящую в оба контура. При емкостной связи между контурами взаимное влияние их друг на друга осуществляется через конденсатор C 1,2, одновременно входящий в оба контура ( рис.104, в ). При определении коэффициента связи, так же как и ранее, напишем выражения для Х св, X 1 и X 2 :
Слайд 12
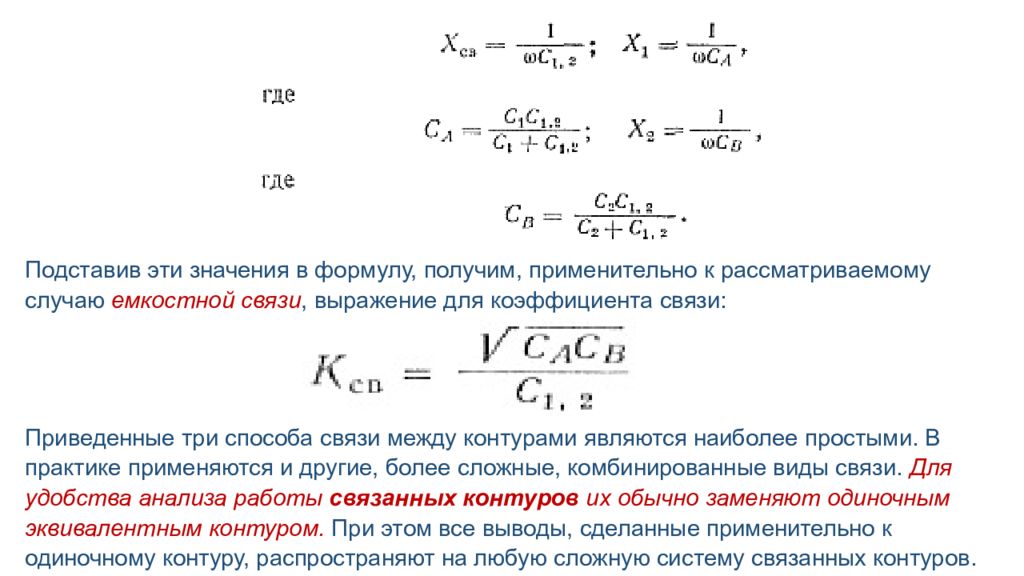
Подставив эти значения в формулу, получим, применительно к рассматриваемому случаю емкостной связи, выражение для коэффициента связи: Приведенные три способа связи между контурами являются наиболее простыми. В практике применяются и другие, более сложные, комбинированные виды связи. Для удобства анализа работы связанных контуров их обычно заменяют одиночным эквивалентным контуром. При этом все выводы, сделанные применительно к одиночному контуру, распространяют на любую сложную систему связанных контуров.
Слайд 13
Коэффициенты связи между другими контурами: • с внутренней индуктивной (автотрансформаторной) связью (см. рис. 3.42, б) • с внешней индуктивной связью (см. рис. 3.42, в) • с внутренней емкостной связью (см. рис. 3.42, г) Коэффициент связи не зависит от частоты и используется для количественной оценки степени связи между контурами. Коэффициент связи между контурами с трансформаторной связью равен коэффициенту связи между входящими в эти контуры индуктивностями:
Слайд 14
• с внешней емкостной связью (см. рис. 3.42, д) Из выражений (3.107)—(3.111) следует, что значение коэффициента связи между контурами k CB не может превышать единицы, причем с увеличением параметра элемента связи (М, L CB, С св ) возрастает коэффициент k CB между контурами с трансформаторной, автотрансформаторной и внешней емкостной связями и уменьшается коэффициент связи между контурами с внешней индуктивной и внутренней емкостной связями.
Слайд 15
Таким образом, систему связанных контуров можно заменить эквивалентным последовательным контуром в виде последовательного соединения активного и реактивного сопротивлений эквивалентного контура. Влияние второго контура на первый заключается в увеличении активных потерь в первом контуре и в изменении его реактивного сопротивления. Активное сопротивление эквивалентного контура всегда больше активного сопротивления первого контура, а реактивное сопротивление эквивалентного контура зависит от знаков Х 1 и Х 2. Резонанс в эквивалентном контуре (в связанных контурах) наступает при Х 1э = 0. Взаимное влияние контуров можно объяснить и при помощи векторной диаграммы
Слайд 16
Векторная диаграмма построена для случая, когда оба контура настроены на частоту э.д.с, приложенной к перво-му контуру, т.е. резонансная частота первого контура ω 01, равна резонансной частоте второго контура ω 02 и обе они совпадают с частотой внешней э.д.с. Из векторной диаграммы видно, что ток в первом контуре совпадает по фазе с внешней э.д.с. Это объясняется тем, что сопротивление настроенного в резонанс контура имеет активный характер. Ток I 1 наводит э. д. с. взаимоиндукции в катушке L 2. Рис. Векторная диаграмма связанных контуров Е М2 отстает по фазе от I 1 на 90°. Ток во втором контуре I 2 наводит в первом контуре э.д.с. взаимоиндукции Е М1 которая отстает по фазе от тока на 90 °. Из векторной диаграммы также видно, что внешняя э. д. с. E и э. д. с. взаимоиндукции Е М1 находятся в противофазе. Последнее вызывает уменьшение тока в первом контуре: так как внешней э. д. с. приходится преодолевать встречную э. д. с. Е М1
Слайд 17
Действительно, когда оба контура настроены в резонанс, т. е. когда X 1 = 0 и Х 2 = 0, ток в первом контуре Влияние второго контура на первый сказывается в форме увеличения сопротивления первого контура на величину вносимого сопротивления R вн, что вызывает уменьшение тока в первом (эквивалентном) контуре.
Слайд 18
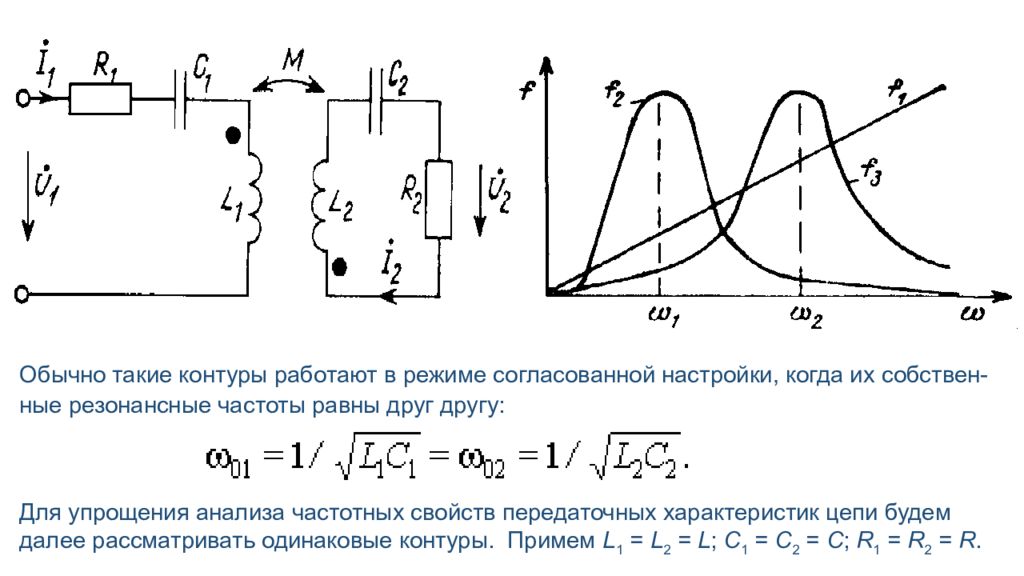
Обычно такие контуры работают в режиме согласованной настройки, когда их собствен-ные резонансные частоты равны друг другу: Для упрощения анализа частотных свойств передаточных характеристик цепи будем далее рассматривать одинаковые контуры. Примем L 1 = L 2 = L ; C 1 = C 2 = C ; R 1 = R 2 = R.
Слайд 19
Поскольку Z н = R ; Z 11 = Z 22 = R + j ( ω L – 1/ ω C ), перепишем это выражение. Частотная зависимость модуля: Представим K U (w) как произведение трех функций частоты : f 1 (ω) = ω MR ; f 2,3 (ω) = Коэффициент передачи по напряжению: изображенных на рис.
Слайд 20
Распишем контурными уравнениями, как для трансформатора. Введем понятие фактора связи, К= Q k, где к – коэффициент связи, Q- добротность. При K=1 связь называется критической.
Слайд 22
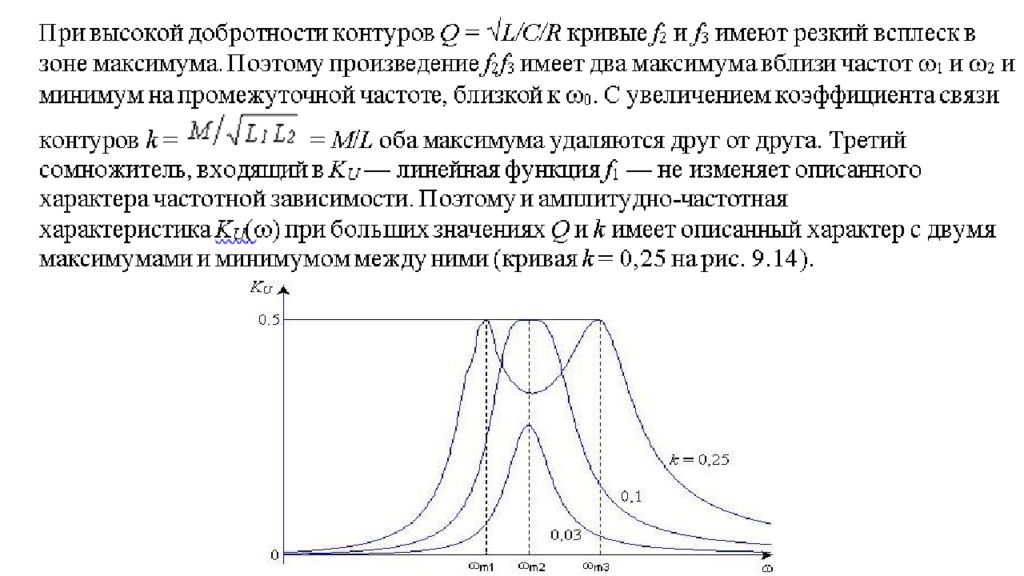
С увеличением значений k и Q провал частотной характеристики усиливается. С уменьшением добротности контуров Q и коэффициента связи k кривые f 2 и f 3 приобретают более плавный характер, их максимумы сближаются. В результате оба максимума кривой K U (ω) сливаются, и амплитудно-частотная характеристика имеет один максимум ω m2 вблизи частоты ω 0 (кривые k = 0,1 и 0,03 на рис. 9.14 ).
Слайд 24
Рис. Резонансные кривые для тока во втором контуре в случае одинаковых контуров. Эта зависимость имеет один максимум при κ < 1 (слабая связь) и два максимума — при κ > 1 (сильная связь между контурами). Значение κ = 1 называется критическим. При критической связи резонансная кривая обладает плоской вершиной и по форме близка к П-образной характеристике идеального полосового фильтра. Произведение коэффициента связи на добротность контура К = k Q называют фактором связи, или параметром связи. Введем обобщенную расстройку x = ζ Q.
Слайд 25
Таким образом, простой способ определения критической связи состоит в измерении зависимости и нахождении ее максимума. На резонансной частоте ω при критической связи реализуется режим передачи максимальной мощности от источника сигнала во второй контур. Полосой пропускания системы связанных контуров называют полосу частот, в пределах которой ток во втором контуре не падает ниже от наибольшего. Для одиночного колебательного контура При критической связи Полоса пропускания связанных контуров при критической связи в раз больше полосы пропускания одиночного контура. Форма резонансной кривой при небольших расстройках характеризуется более плоской вершиной в полосе пропускания и более крутым спадом в полосе подавления. При связи меньше критической резонансная кривая имеет один максимум. Связанные контуры имеют полосу пропускания как у одиночного контура, при При очень слабой связи то есть полоса пропускания связанных контуров оказывается уже, чем полоса одиночного контура.
Слайд 27
ξ — обобщенная расстройка. Принято, что при построении резонансной кривой контура с достаточно большой добротностью можно принять множитель и при вычислении добротности Q считать. Это, конечно, справедливо при достаточно малых расстройках (например, при ξ =3 и Q=20 получается. Резонансная кривая: Если kQ <<1 — слабая связь контуров, то
Слайд 28
Резонансная кривая имеет один максимум при ξ = 0, т. е. при Ток меньше в раз (границы полосы пропускания) при а у последовательного контура и на границах полосы пропускания Следовательно, полоса пропускания связанных контуров при слабой связи меньше, чем у последовательного контура. При kQ = 1 — критической связи и на границах полосы пропускания т. е. полоса пропускания больше, чем у последовательного контура. При kQ > 1 — сильной связи получается резонансная кривая с двумя максимумами. Если считать, что на границе полосы пропускания значение тока, как и у последовательного контура, в раз меньше максимального, то получится полоса пропускания в 3,1 раза шире и ближе к прямоугольной, чем у последовательного контура при той же добротности контуров, что может быть важным достоинством цепи при построении систем с большой полосой пропускания (широкополосных ). Значение тока зависит от коэффициента связи контуров. Наибольшее значение можно найти обычным исследованием на максимум. Оно получается при и.
Слайд 29
Аналогично исследуются «частные резонансы». Первый частный резонанс достигается изменением емкости (или индуктивности) первого контура. При резонансе и ток совпадает по фазе с напряжением Для получения второго частного резонанса добиваются максимального значения тока изменением емкости (или индуктивности) второго контура. «Сложный резонанс» получается при изменении параметров одного из контуров и коэффициента связи.