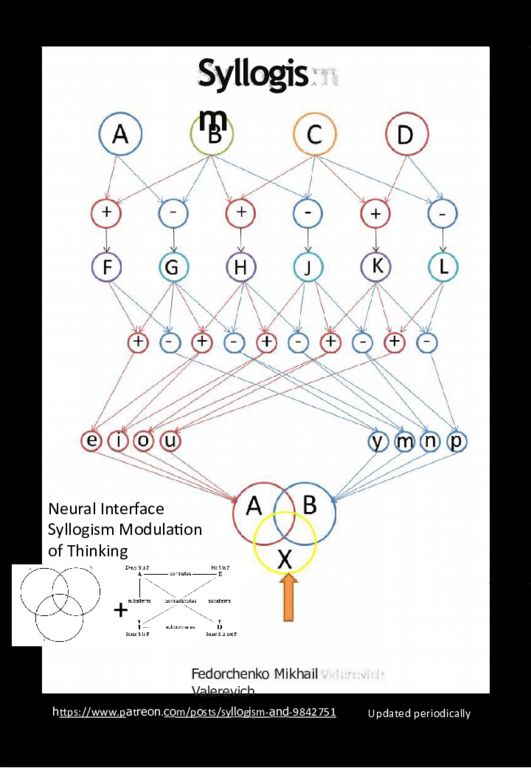
Fedorchenko Mikhail Valerevich h ttps://www.p a t reon. co m/p o sts/sy llo g i sm- and -9842751 Updated periodically + Neural Interface Syllogism Modulation of Thinking
Subj e c t i v e P r oo f Experience Practice T h e o r y X Statemen P S Pr T h E x
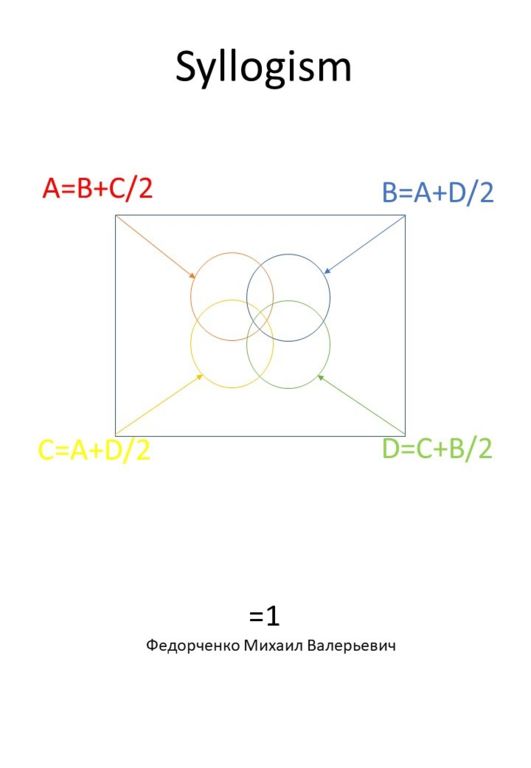
The result of a syllogism depends on the particular logical operation. Assuming the scheme uses the standard AND operation, the results are as follows: - **\\( A = 0, B = 0 \) → 0** - **\\( A = 1, B = 0\) → 0** - **\\( A = 0, B = 1 \) → 0** - **\( A = 1, B = 1 \) → 1** If OR is used: - **\( A = 0, B = 0 \) → 0** - **\\( A = 1, B = 0 \) → 1** - **\*( A = 0, B = 1 \) → 1** - **\( A = 1, B = 1 \) → 1** Without specific indications of the logical operations used, two interpretations (AND and OR) can be proposed. However, based on the most likely approach (the logical operation AND), the latter case \( A = 1, B = 1 \) will lead to a true result (1), while all other combinations will lead to a false result (0).
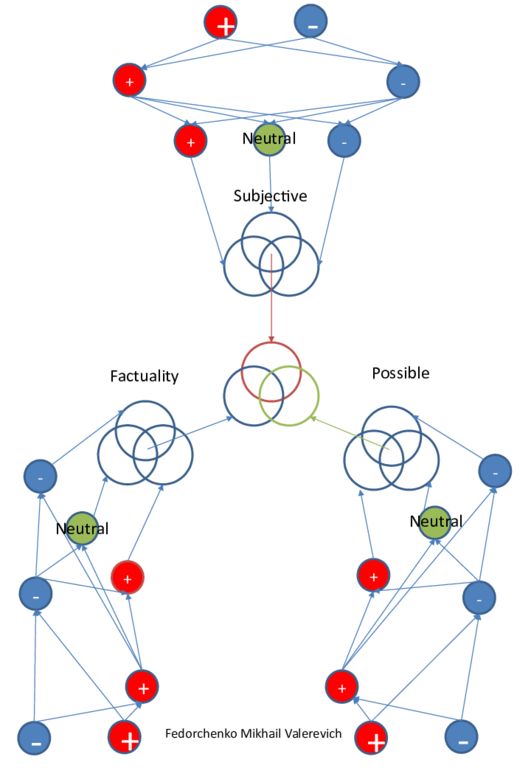
+ - + - - + - + + - + - + - - + + - Subjective Factuality Possible Fedorchenko Mikhail Valerevich Neutral Neutral Neutral
=1
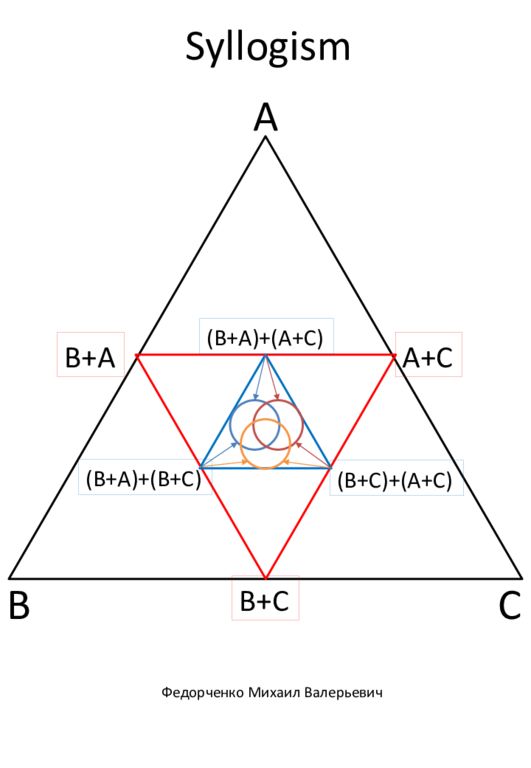
A B C B+C B+A A+C (B+A)+(A+C) (B+A)+(B+C) (B+C)+(A+C) Федорченко Михаил Валерьевич Syllogism
Got it, you've provided sets of values for the variables \(A\), \(B\) and \(C\) (0 or 1), and now you need to determine whether the result is 1 or 0 for each case. Let's look at the basic expressions in the triangle: 1. **(B + A) + (A + C)** 2. **(B + A) + (B + C)** 3. **(B + C) + (A + C)** The value of the expression depends on the values of the variables \(A\), \(B\), and \(C\). ### Logical Operations: - Adding the logical variables \(A + B\) gives 1 if at least one of \(A\) or \(B\) is 1. - If both are 0, the result is 0. - Adding two expressions \(X + Y\) is also 1 if at least one of them is 1. #### Consider each set of values: 1. **\\(A = 0\), \(B = 0\), \(C = 0\)**. - \((B + A) + (A + C) = (0 + 0) + (0 + 0) = 0 + 0 = 0\) - \((B + A) + (B + C) = (0 + 0) + (0 + 0) = 0 + 0 = 0\) - \((B + C) + (A + C) = (0 + 0) + (0 + 0) = 0 + 0 = 0\) - **Result: 0** 2. **\\(A = 1\), \(B = 0\), \(C = 0\)**. - \((B + A) + (A + C) = (0 + 1) + (1 + 0) = 1 + 1 = 1\) - \((B + A) + (B + C) = (0 + 1) + (0 + 0) = 1 + 0 = 1\) - \((B + C) + (A + C) = (0 + 0) + (1 + 0) = 0 + 1 = 1\) - **Result: 1** 3. **\\(A = 0\), \(B = 0\), \(C = 1\)**. - \((B + A) + (A + C) = (0 + 0) + (0 + 1) = 0 + 1 = 1\) - \((B + A) + (B + C) = (0 + 0) + (0 + 1) = 0 + 1 = 1\) - \((B + C) + (A + C) = (0 + 1) + (0 + 1) = 1 + 1 = 1\) - **Result: 1** 4. **\(A = 1\), \(B = 1\), \(C = 0\)**. - \((B + A) + (A + C) = (1 + 1) + (1 + 0) = 1 + 1 = 1\) - \((B + A) + (B + C) = (1 + 1) + (1 + 0) = 1 + 1 = 1\) - \((B + C) + (A + C) = (1 + 0) + (1 + 0) = 1 + 1 = 1\) - **Result: 1** 5. **\(A = 1\), \(B = 0\), \(C = 1\)**. - \((B + A) + (A + C) = (0 + 1) + (1 + 1) = 1 + 1 = 1\) - \((B + A) + (B + C) = (0 + 1) + (0 + 1) = 1 + 1 = 1\) - \((B + C) + (A + C) = (0 + 1) + (1 + 1) = 1 + 1 = 1\) - **Result: 1** 6. **\(A = 1\), \(B = 1\), \(C = 1\)**. - \((B + A) + (A + C) = (1 + 1) + (1 + 1) = 1 + 1 = 1\) - \((B + A) + (B + C) = (1 + 1) + (1 + 1) = 1 + 1 = 1\) - \((B + C) + (A + C) = (1 + 1) + (1 + 1) = 1 + 1 = 1\) - ### Score: 1** ### Totals: For your given sets of variable values \(A\), \(B\), \(C\): - For the set \(0, 0, 0\), the result is 0. - For all other sets ( \(1, 0, 0\); \(0, 1, 0 \); \(0, 0, 1\); \(1, 1, 0\); \(1, 0, 1\); \(1, 1, 1\) ), the result is 1.
https://archive.org/754189189-syllogism-and-syllogistic-syllogistic-intellectus-cognitum/Logic_of_Being-Syllogism-and-Syllogistic-Syllogistic-intellectus-cognitum.pptx https://archive.org/details/logic-of-being-statements
