Слайд 2
«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем… ». Иоганн Кеплер
Слайд 3: История «Золотого сечения»
В Древнем Египте существовала «система правил гармонии», основанная на Золотом Сечении. В Древней Греции Золотое Сечение было своеобразным каноном культуры, который пронизывает все сферы науки и искусства. Красота и гармония стали важнейшими категориями познания. В толковании древних греков понятие золотого сечения, и понятие гармонии идентичны. Согласно Пифагору гармония имеет численное выражение, то есть, она связана с концепцией числа. Евклид излагает теорию Платоновых тел, которая является существенным разделом геометрической теории Золотого Сечения. Теория гармонии Древних
Слайд 4
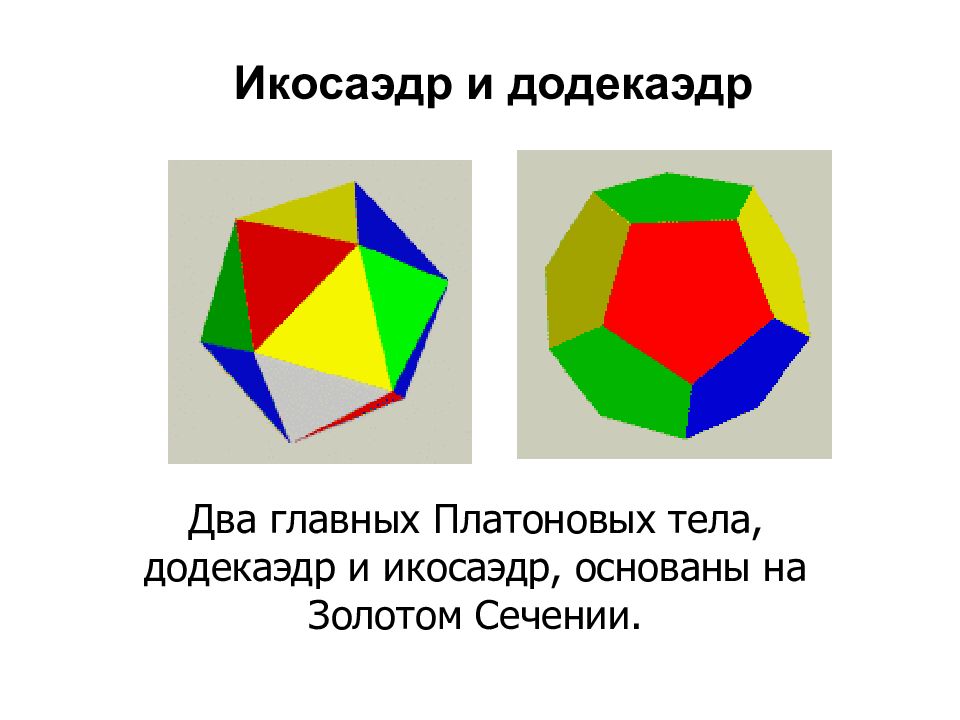
Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом Сечении. Икосаэдр и додекаэдр
Слайд 5: Золотая Пропорция» - главный эстетический принцип эпохи Средневековья
Эпоха Возрождения ассоциируется с именами таких «титанов», как Леонардо да Винчи, Микеланджело, Рафаэль, Николай Коперник, Альберт Дюрер, Лука Пачоли. Имеется много авторитетных свидетельств о том, что именно Леонардо да Винчи(1452-1519) был одним из первых, кто ввел сам термин «Золотое Сечение». Доказано, что во многих своих произведениях Леонардо да Винчи использовал пропорции золотого сечения, в частности, в своей всемирно известной фреске «Тайная вечеря» и непревзойденной « Джоконде».
Слайд 6: Витрувийский человек» Леонардо да Винчи
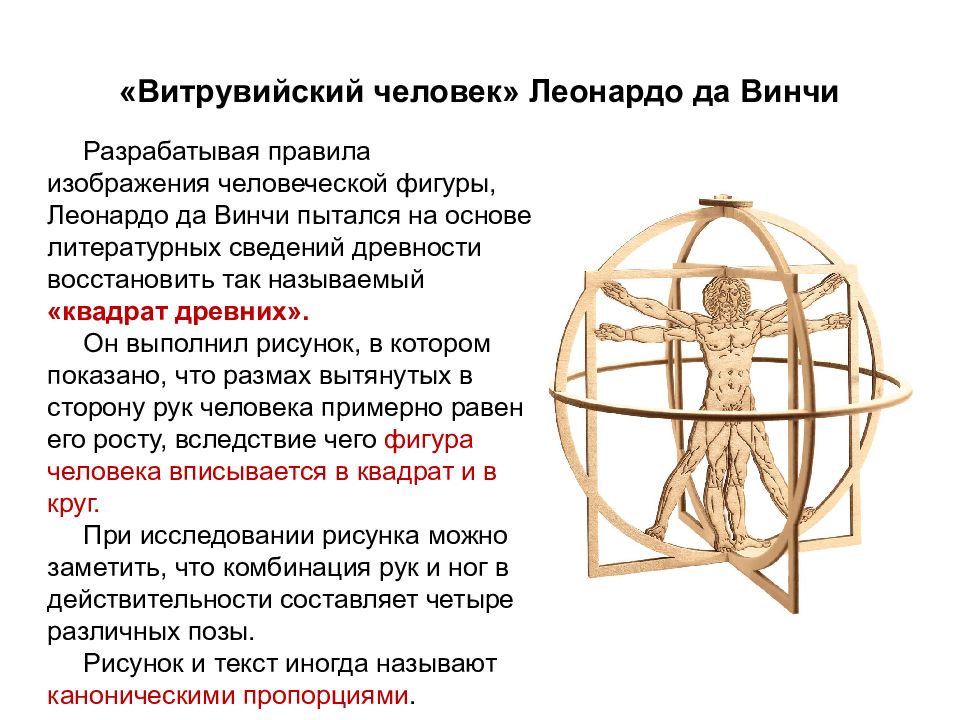
Разрабатывая правила изображения человеческой фигуры, Леонардо да Винчи пытался на основе литературных сведений древности восстановить так называемый «квадрат древних». Он выполнил рисунок, в котором показано, что размах вытянутых в сторону рук человека примерно равен его росту, вследствие чего фигура человека вписывается в квадрат и в круг. При исследовании рисунка можно заметить, что комбинация рук и ног в действительности составляет четыре различных позы. Рисунок и текст иногда называют каноническими пропорциями.
Слайд 7: Ряд Фибоначчи
С историей золотого сечения связано имя итальянского математика Леонардо Фибоначчи. Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Каждый член последовательности, начиная с третьего, равен сумме двух предыдущих, а отношение смежных чисел ряда приближается к отношению золотого деления. Все исследователи золотого деления в растительном и в животном мире, искусстве, неизменно приходили к ряду Фибоначчи как арифметическому выражению закона золотого деления.
Слайд 8: Вклад Кеплера в теорию Золотого Сечения
Гениальный астроном Иоганн Кеплер (1571-1630) был последовательным приверженцем Золотого Сечения, Платоновых тел и Пифагорейской доктрины о числовой гармонии Мироздания. Считается, что именно Кеплер обратил внимание на ботаническую закономерность филлотаксиса и установил связь между числами Фибоначчи и золотой пропорцией, доказав, что последовательность отношений соседних чисел Фибоначчи: 1/1; 2/1; 3/2; 5/3 ;8/5; 13/8;… в пределе стремится к золотой пропорции
Слайд 9: Золотое сечение в природе
Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали. Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Паук плетет паутину спиралеобразно.
Слайд 10: Золотое сечение лист розы
Величины отростков и лепестков цикория подчинены правилу золотой пропорции.
Слайд 14
Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках "упакованы" по логарифмическим ("золотым") спиралям, завивающимся навстречу друг другу, причем числа "правых "и "левых" спиралей всегда относятся друг к другу, как соседние числа Фибоначчи.
Слайд 15: Рога и бивни животных развиваются в форме спирали. Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль
Слайд 16
Золотая пропорция в теле ящерицы – длина хвоста так относится к длине остального тела, как 62 к 38.
Слайд 17
У многих бабочек узоры на крыльях, соотношение размеров грудной и брюшной части тела соответствуют золотой пропорции
Слайд 18
Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.
Слайд 19
Соотношение воды и суши на планете Земля составляет 62% и 38%. У Земли отношение радиусов равно числу золотого сечения в первой степени
Слайд 21: Математическая эстетика Цейзинга
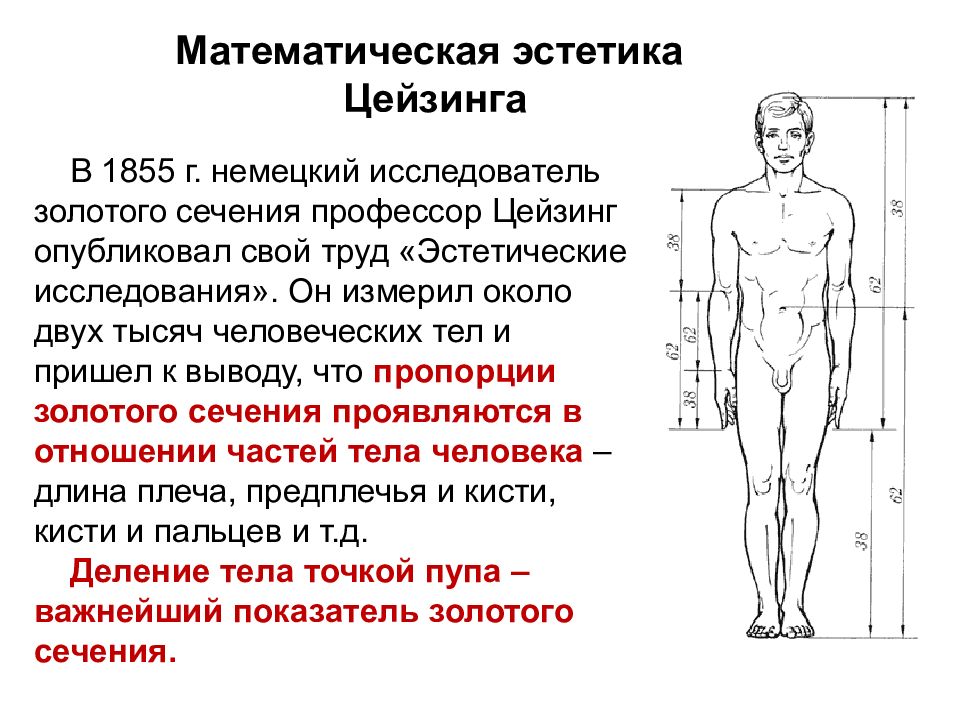
В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он измерил около двух тысяч человеческих тел и пришел к выводу, что пропорции золотого сечения проявляются в отношении частей тела человека – длина плеча, предплечья и кисти, кисти и пальцев и т.д. Деление тела точкой пупа – важнейший показатель золотого сечения.
Слайд 22: Результаты измерений учащихся
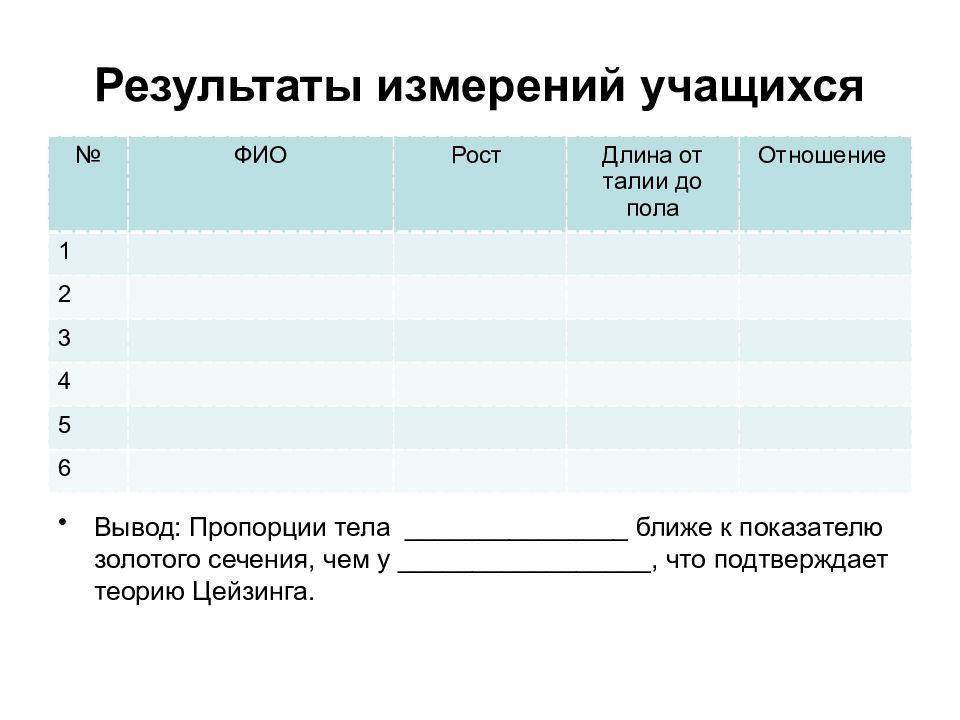
№ ФИО Рост Длина от талии до пола Отношение 1 2 3 4 5 6 Вывод: Пропорции тела _______________ ближе к показателю золотого сечения, чем у _________________, что подтверждает теорию Цейзинга.
Слайд 23
Сердце бьется непрерывно – от рождения до его смерти. Его работа должна быть оптимальной. Отклонения от оптимального режима вызывают различные заболевания. В.Цветков установил, что у человека оптимальная «золотая» частота сердцебиения,составляет 63 удара в минуту. Он также установил, что систолическое (нижнее) давление крови в аорте равно 0,382, а диастолическое (верхнее) - 0,618 от среднего давления крови в аорте. Таким образом, работа сердца, изменения давления крови оптимизировано по одному и тому же принципу- по правилу золотой пропорции.
Слайд 24
В качестве примера построения скрипки на основе закона золотого сечения возьмем скрипку работы Антонио Страдивари, созданную им в 1700 г. Длина корпуса 355 мм Ширина верхнего овала 167,5 мм Ширина нижнего овала 207 мм Ширина средней части 109 мм Золотое сечение в музыке
Слайд 25
Известно также, что скрипка благотворно действует на меланхоликов, альт эффективен при нарушениях нервной системы и упадке сил — отлично влияет при этом на флегматиков. Арфа помогает при истерии, флейта — при заболеваниях бронхолегочной системы и от несчастной любви, а кларнет избавляет от подавленного состояния. При депрессии и психозе показаны элегии, ноктюрны, колыбельные... Пятая “ Лунная соната ” Бетховена снимает раздражительность и озлобленность, а гипертоникам рекомендуют слушать музыку из балета “ Лебединое озеро ” Чайковского, Ноктюрн ре минор Шопена и Концерт ре минор для скрипки Баха. Оказывается, они снижают кровяное давление...
Слайд 26
Н. Васютинский констатирует: "Кульминацией главы является объяснение Евгения в любви к Татьяне - строка "Бледнеть и гаснуть... вот блаженство!". Эта строка делит всю восьмую главу на две части - в первой 477 строк, а во второй - 295 строк. Их отношение равно 1,617! Тончайшее соответствие величине золотой пропорции! Это великое чудо гармонии, совершенное гением Пушкина!". Золотое сечение в литературе Евгений Онегин
Слайд 27
Сенсационное открытие сделал петербургский поэт и переводчик “Слова о полку Игореве” Андрей Чернов. Он нашел, что построение стихов загадочного древнерусского памятника подчиняется математическим законом. Исследования позволили сделать Чернову заключение о том, что в основу “Слова о полку Игореве”, состоящего из девяти песен, легла круговая композиция. Уже первые расчеты стали подтверждать закономерность, да еще какую! Если число стихов во всех трех частях (их 804) разделить на число стихов в первой и последней части (256), получается 3,14, т.е. число с точностью до третьего знака. Слово о полку Игореве
Слайд 28
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.). Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада. Золотое сечение в архитектуре
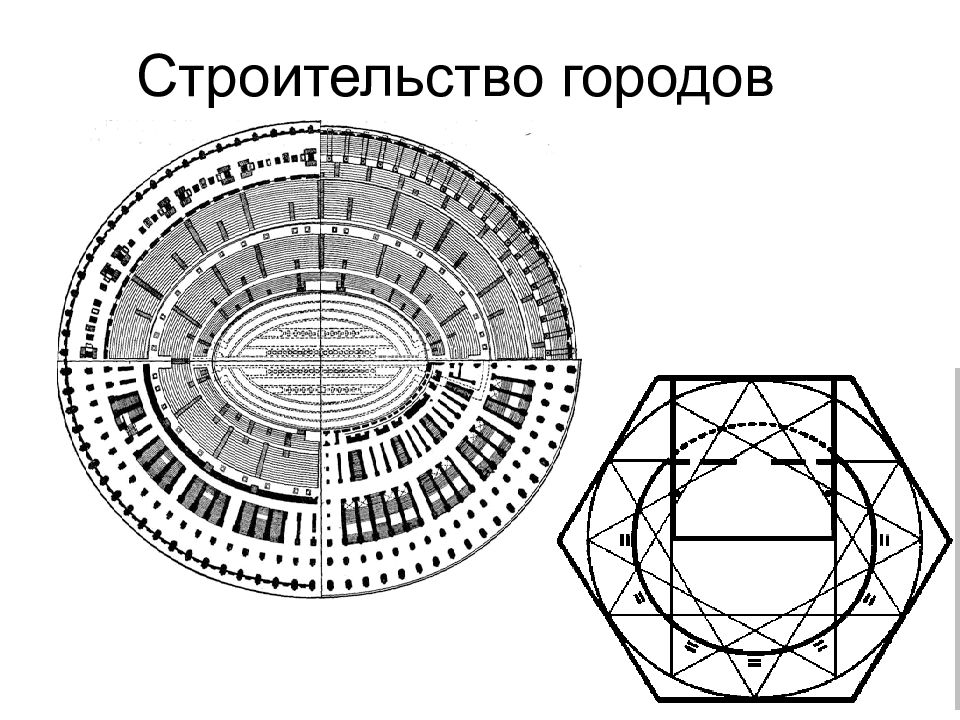
Слайд 29: Строительство
Римский архитектор Ветрувий считал, что при планировки городов улицы спланировать нужно так, чтобы вдоль них не дули основные ветра.
Слайд 30
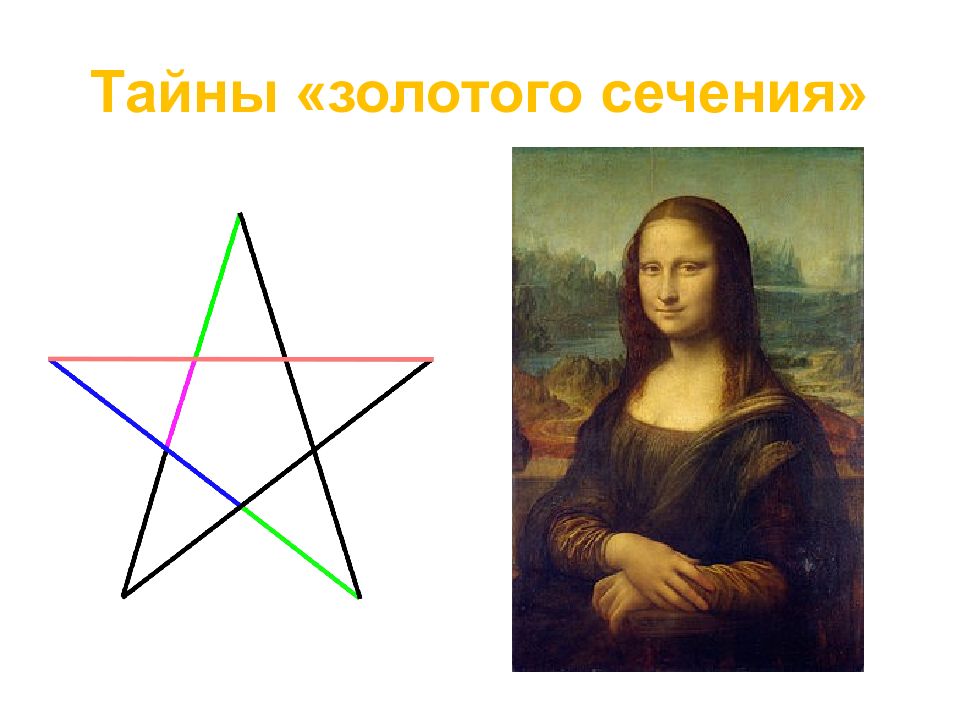
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды». Золотое сечение в живописи
Слайд 31
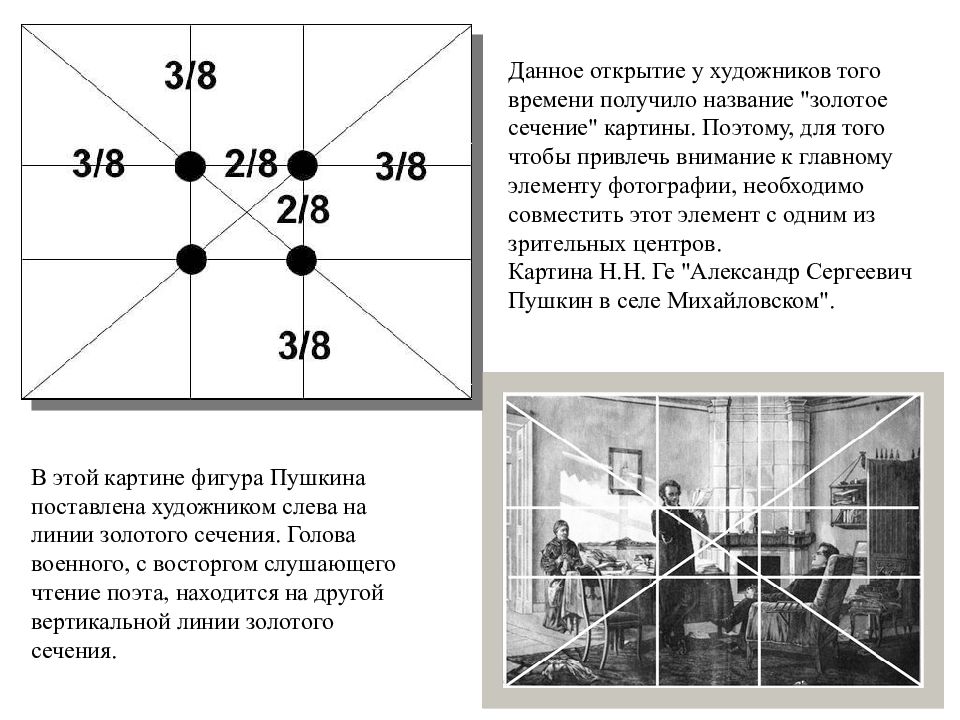
Данное открытие у художников того времени получило название "золотое сечение" картины. Поэтому, для того чтобы привлечь внимание к главному элементу фотографии, необходимо совместить этот элемент с одним из зрительных центров. Картина Н.Н. Ге "Александр Сергеевич Пушкин в селе Михайловском". В этой картине фигура Пушкина поставлена художником слева на линии золотого сечения. Голова военного, с восторгом слушающего чтение поэта, находится на другой вертикальной линии золотого сечения.
Слайд 32
Рассмотрим отрезок АВ. А С В Его можно разделить точкой С на две части бесконечным множеством способов, но говорят что точка С производит золотое сечение отрезка АВ, Если выполняется пропорция: длина меньшего отрезка так относится к длине большего, как больший отрезок относится к длине всего отрезка, т.е. СВ АС АС АВ = . (1)
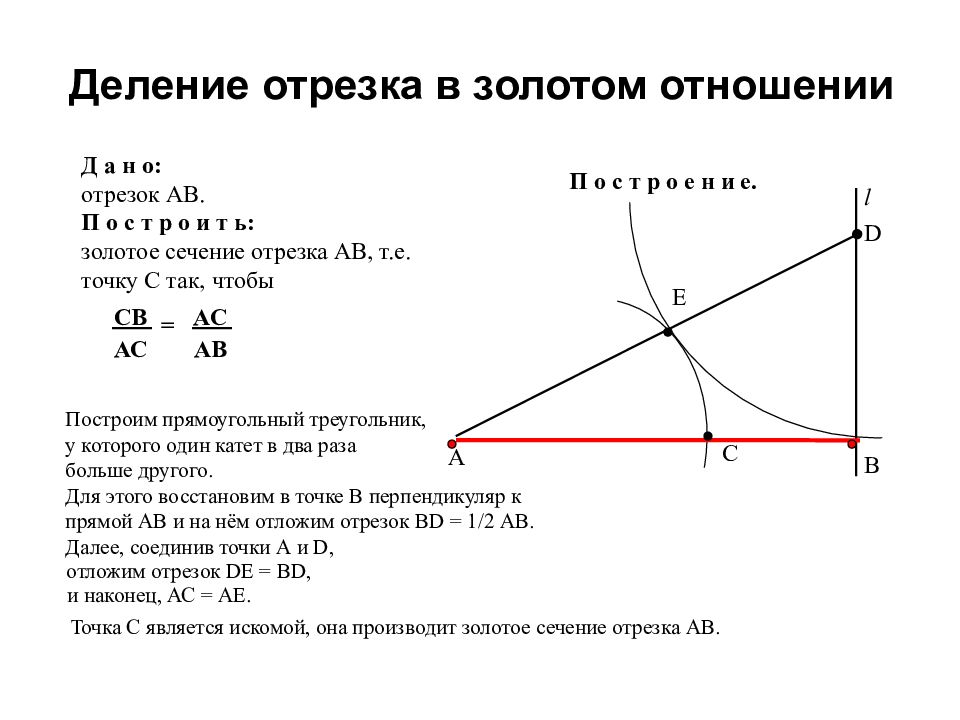
Слайд 33: Деление отрезка в золотом отношении
Д а н о: отрезок АВ. П о с т р о и т ь: золотое сечение отрезка АВ, т.е. точку С так, чтобы П о с т р о е н и е. СВ АС АС АВ = А В Е Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нём отложим отрезок BD = 1/2 AB. ●D l Точка С является искомой, она производит золотое сечение отрезка АВ. Далее, соединив точки А и D, отложим отрезок DЕ = ВD, и наконец, АС = АЕ. C
Слайд 34
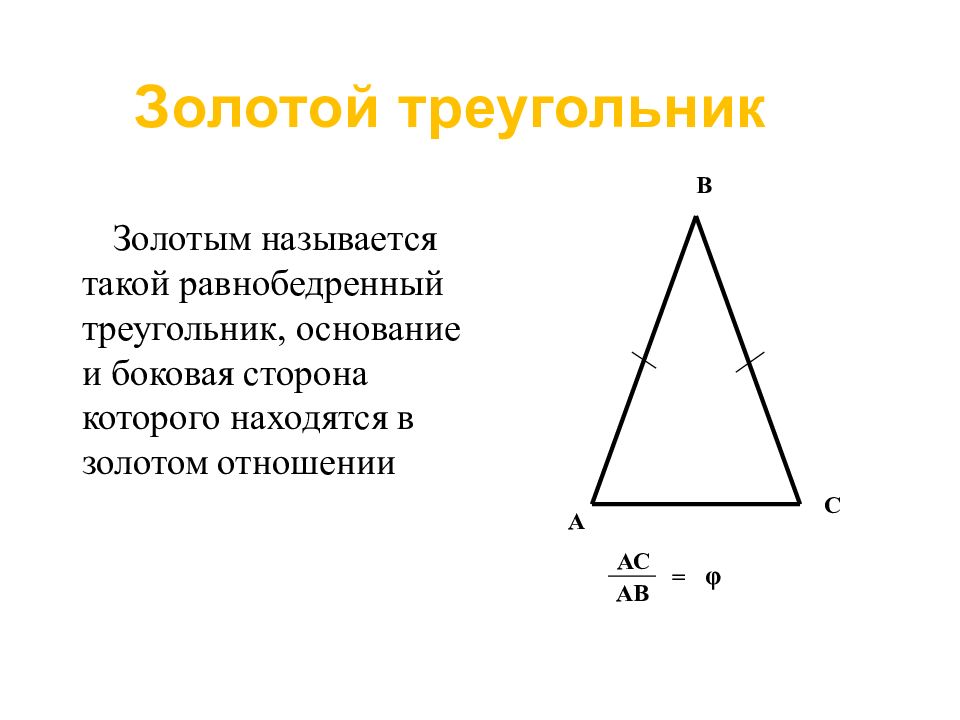
Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении В А С φ АС АВ = Золотой треугольник
Слайд 35
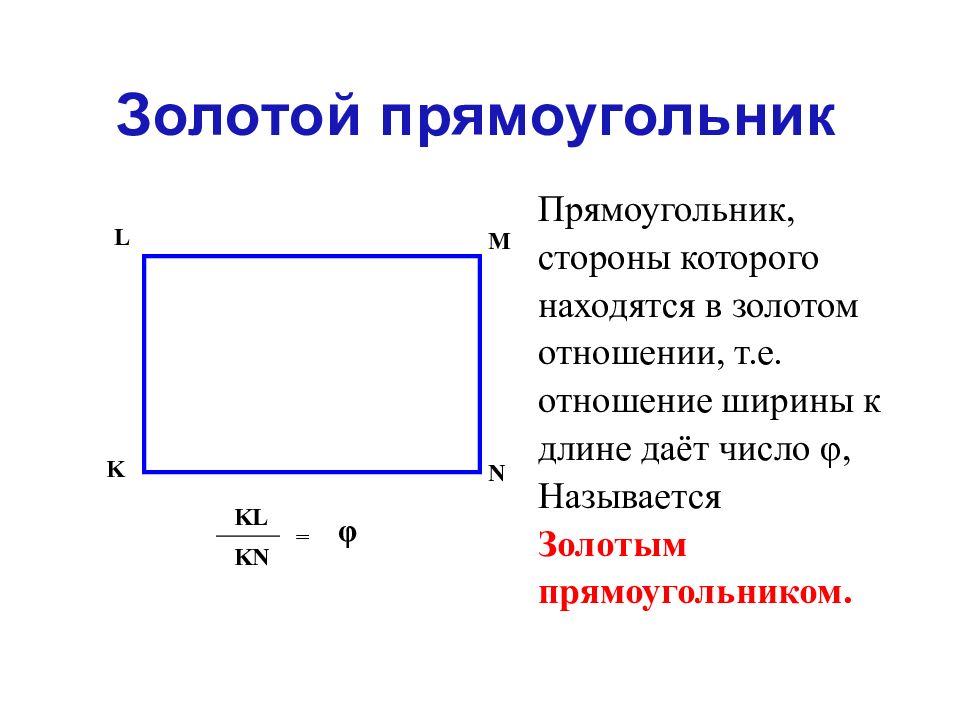
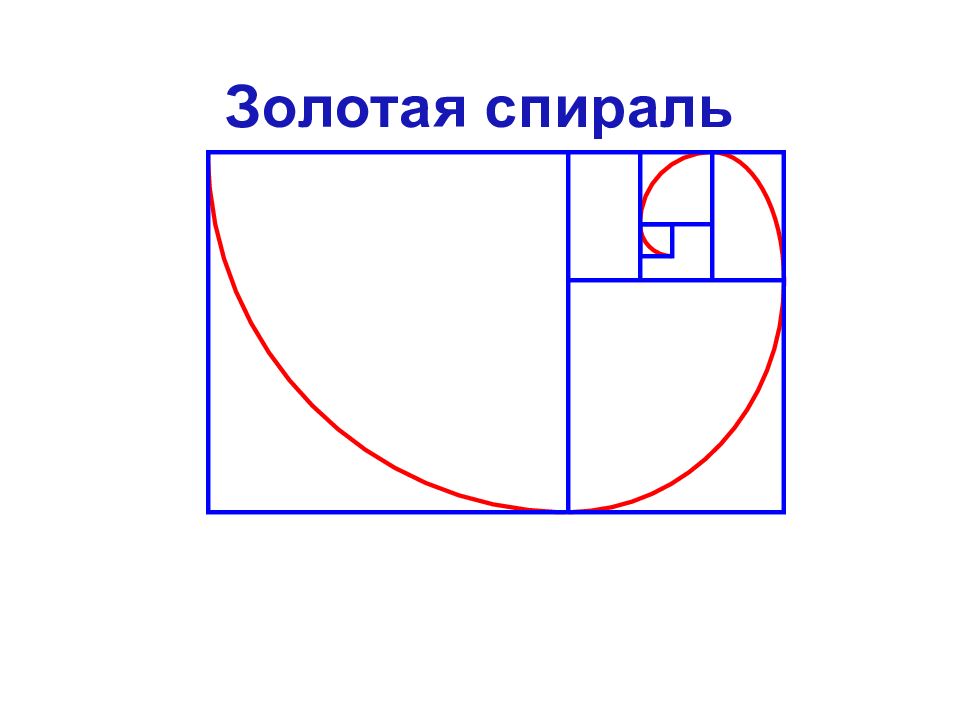
Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение ширины к длине даёт число φ, Называется Золотым прямоугольником. L K M N φ KL KN = Золотой прямоугольник
Слайд 36
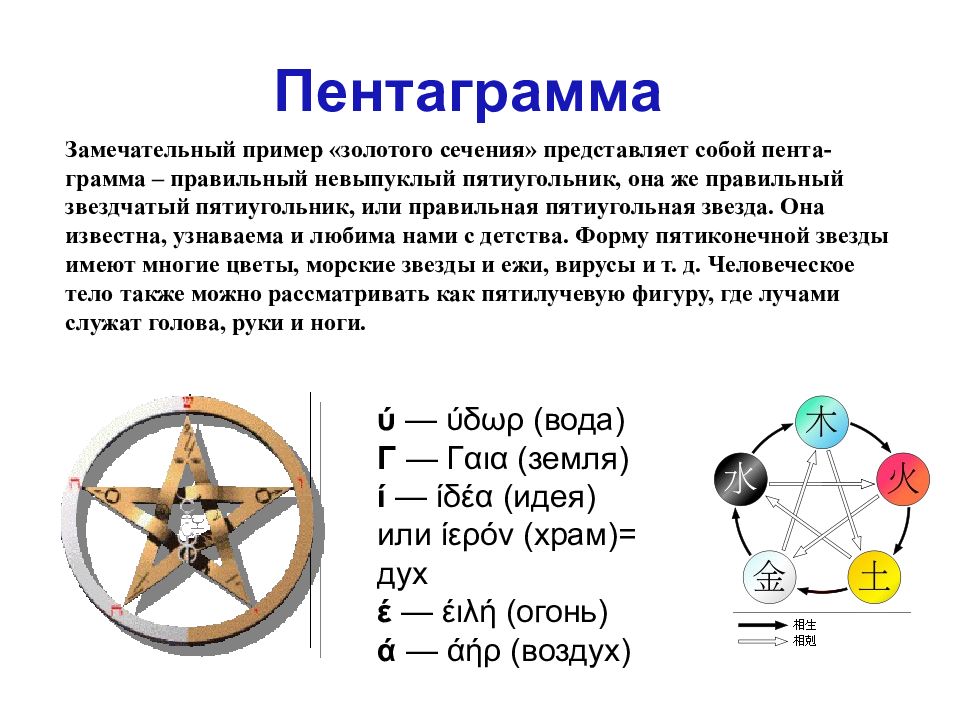
Замечательный пример «золотого сечения» представляет собой пента- грамма – правильный невыпуклый пятиугольник, она же правильный звездчатый пятиугольник, или правильная пятиугольная звезда. Она известна, узнаваема и любима нами с детства. Форму пятиконечной звезды имеют многие цветы, морские звезды и ежи, вирусы и т. д. Человеческое тело также можно рассматривать как пятилучевую фигуру, где лучами служат голова, руки и ноги. Пентаграмма ύ — ύδωρ ( вода) Γ — Γαια ( земля) ί — ίδέα ( идея) или ίερόν ( храм )= дух έ — έιλή ( огонь) ά — άήρ ( воздух)
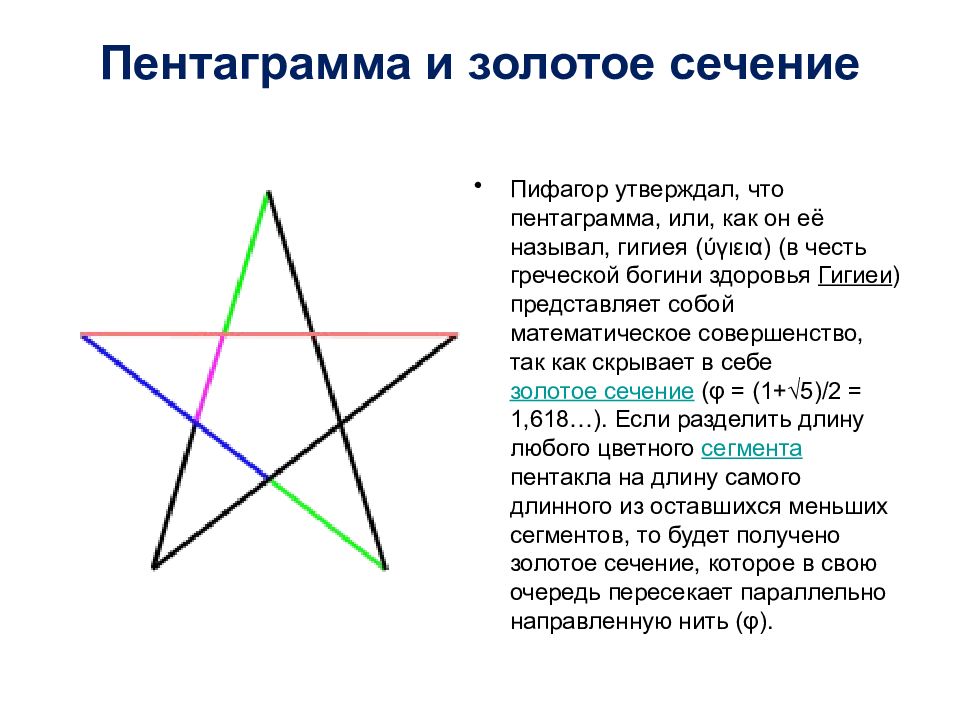
Слайд 37: Пентаграмма и золотое сечение
Пифагор утверждал, что пентаграмма, или, как он её называл, гигиея ( ύγιει α) (в честь греческой богини здоровья Гигиеи ) представляет собой математическое совершенство, так как скрывает в себе золотое сечение (φ = (1+√5)/2 = 1,618…). Если разделить длину любого цветного сегмента пентакла на длину самого длинного из оставшихся меньших сегментов, то будет получено золотое сечение, которое в свою очередь пересекает параллельно направленную нить (φ).