ЛИТЕРАТУРА: Справочник учителя начальной школы. Математика/ А.С. Добротворский, Л.П. Ковригина, И.С. Ордынкина и др. – М. : Дрофа, 2007. – 158 с. Баймарукова П.У. Методика обучения математике в начальных классах/ П.У. Байрамукова, А.У. Уртенова – Ростов н/Д : Феникс, 2009. – 299 с. Белошистая А. В. Методика обучения математике в начальной школе: курс лекций: учебное пособие для студентов вузов, обучающихся по спец. «Педагогика и методика начального образования». – М. : ВЛАДОС, -2007.- 455с. Калиниченко А. В. Методика преподавания начального курса математики / А. В. Калиниченко, Р. Н. Шикова, Е. Н. Леонович. – М. : Академия, 2013. – 208 с.
ПЛАН ЛЕКЦИИ Понятие «текстовая задача». Моделирование в процессе решения текстовых задач. Методы и способы решения текстовых задач. Формы записи решения задач. Этапы решения текстовой задачи и приемы их выполнения.
1. Понятие «текстовая задача» Понятие задача относится к числу общенаучных. В начальном курсе математики понятие задача используется тогда, когда идет речь об арифметических задачах, сформулированных в виде текста. Такие задачи называются «текстовыми» или «сюжетными».
ТЕКСТОВАЯ ЗАДАЧА УСЛОВИЕ ТРЕБОВАНИЕ
В условии задачи указываются связи между данными числами, а также между данными и искомым – эти связи определяют выбор арифметических действий, необходимых для решения задачи.
« Решить задачу – значит раскрыть связи между данными и искомым, заданных условием задачи, на основе чего выбрать, а затем выполнить арифметические действия и дать ответ на вопрос задачи» (М. А. Бантова, Г. В. Бельтюкова).
2. Моделирование в процессе решения текстовых задач Модель – искусственно созданный объект в виде схемы, чертежа, математической формулы, выражения, записи решения и другого.
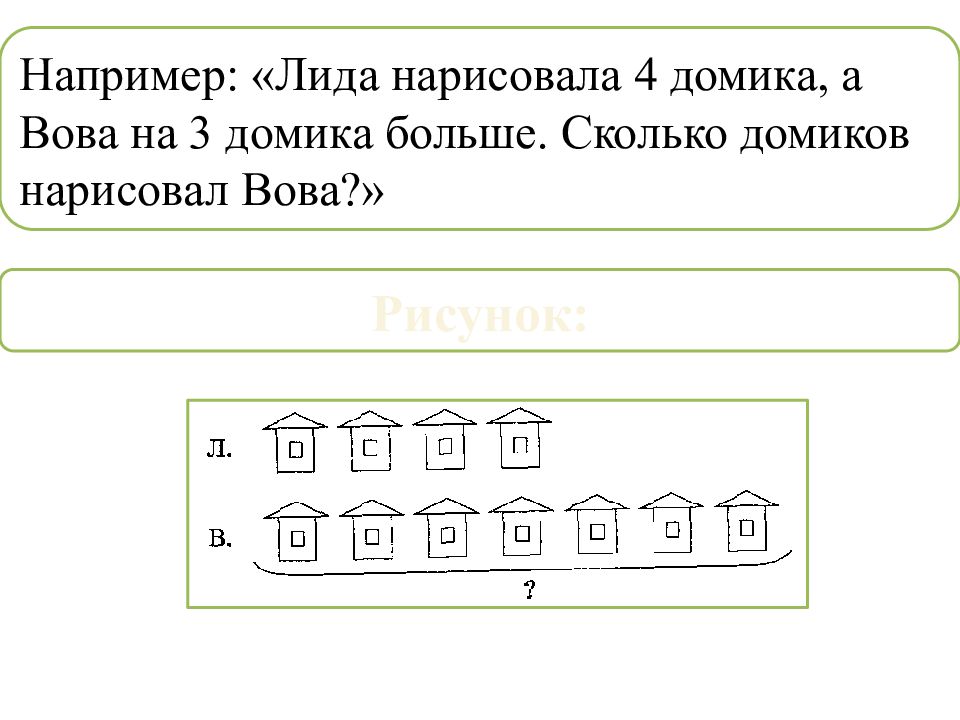
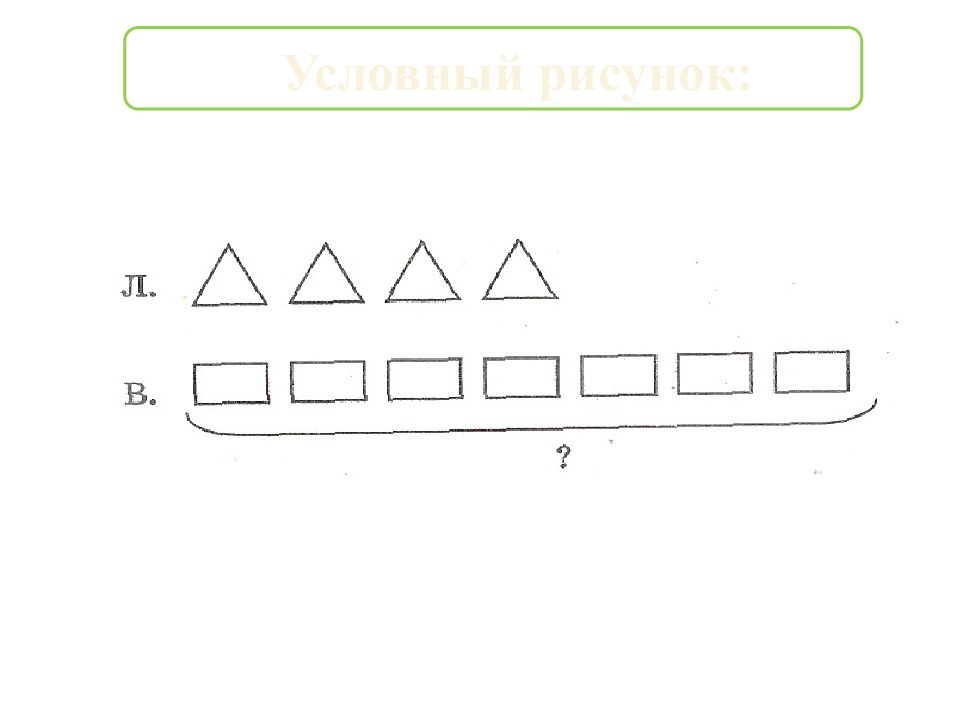
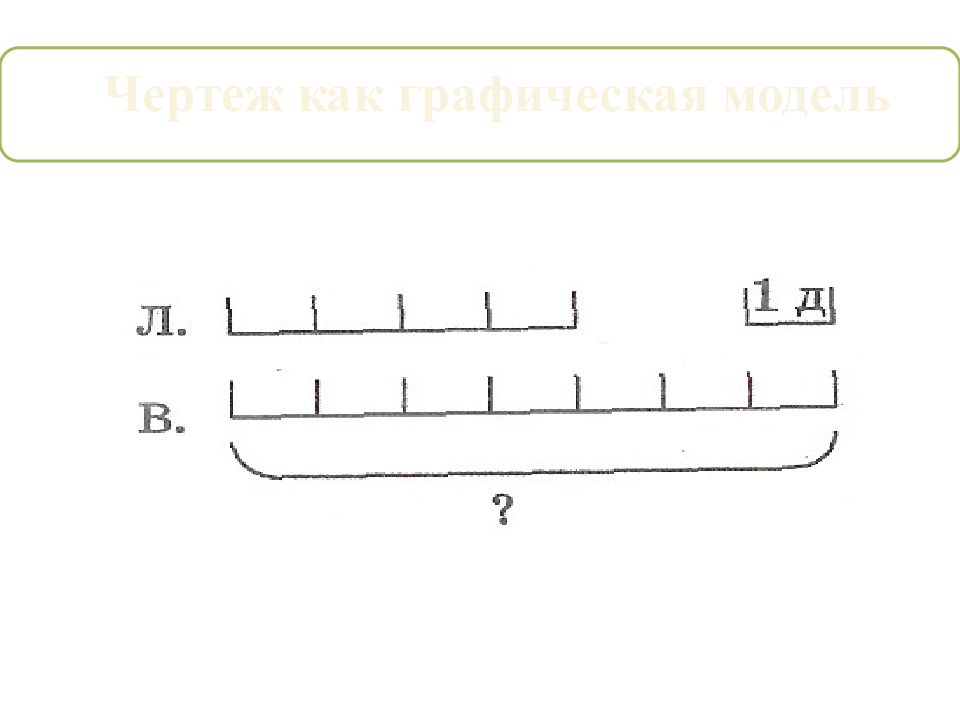
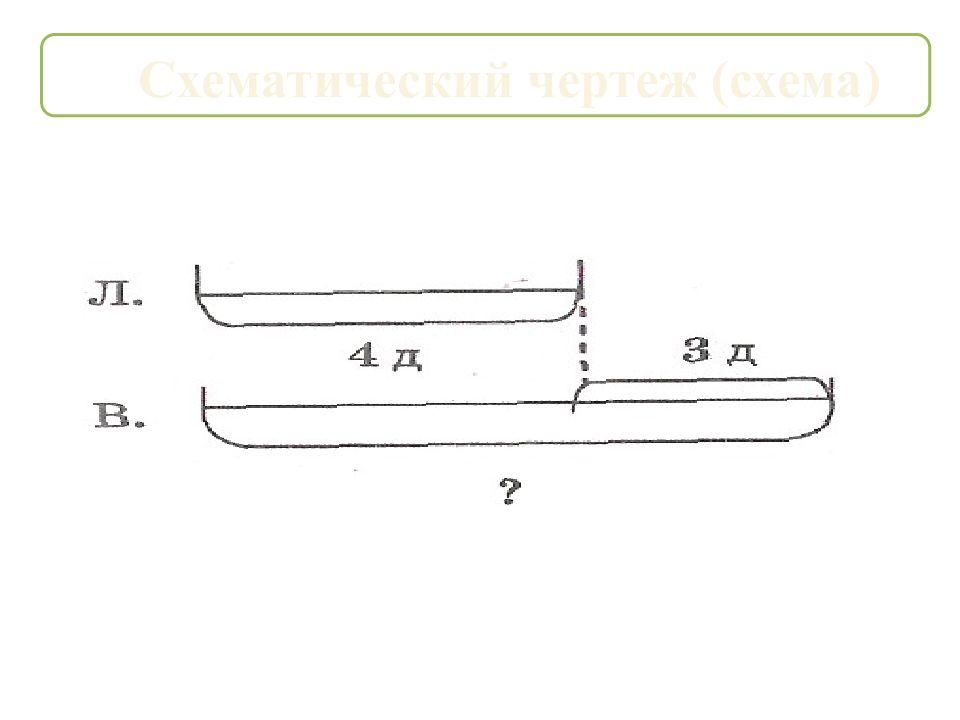
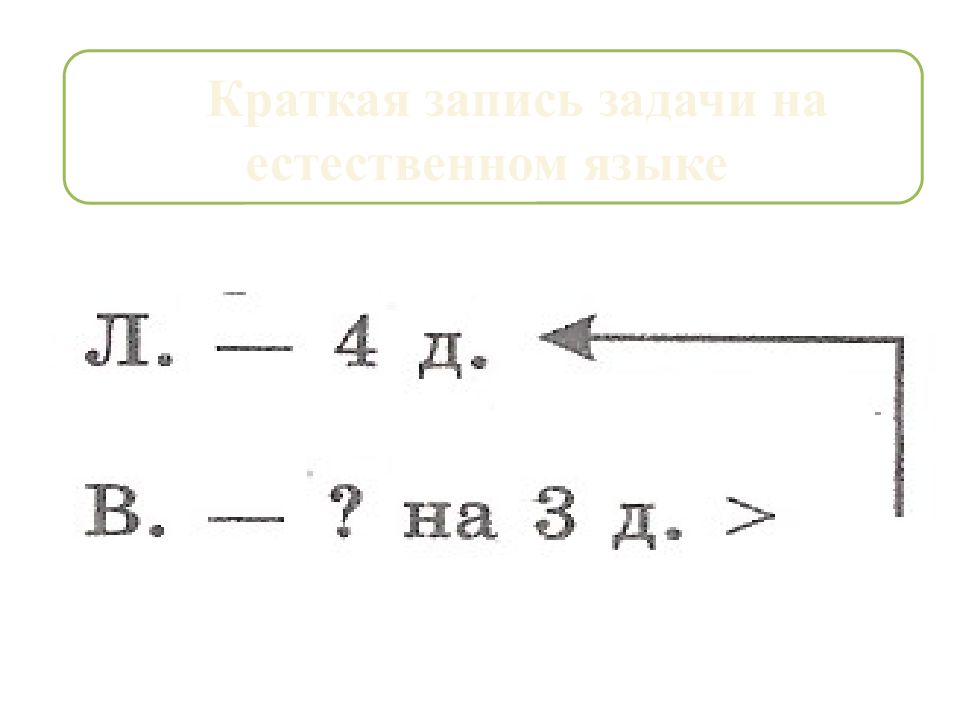
Например: «Лида нарисовала 4 домика, а Вова на 3 домика больше. Сколько домиков нарисовал Вова?» Рисунок:
Условный рисунок:
Чертеж как графическая модель
Схематический чертеж (схема)
Краткая запись задачи на естественном языке
Цена Количество Стоимость ? одинак. 20 м ? м 960 р. 288 р. Таблица (задачи связанные с пропорциональными величинами) Задача. 20 м ткани стоят 960 рублей. Сколько такой ткани можно купить на 288 рублей?
Так как модель – это своеобразная копия задачи, то на ней должны быть представлены все ее объекты, все отношения между ними, указаны требования.
3. Методы и способы решения текстовых задач Основными методами решения текстовых задач являются алгебраический и арифметический.
Решить задачу арифметическим методом - это значит найти ответ на требование задачи посредством выполнения арифметических действий над числами.
Одну и ту же задачу можно решить различными арифметическими способами. Они отличаются друг от друга логикой рассуждений, выполняемых в процессе решения задачи.
Например: Сшили 3 платья, расходуя на каждое по 4 м ткани. Сколько кофт можно сшить из этой ткани, если расходовать на одну кофту 2 м? 2 способ 1) 4 : 2 = 2 (раза) - во столько раз больше идет ткани на платье, чем на кофту; 2) 3 – 2 = 6 (к) - столько кофт можно сшить. 1 способ 1) 4 • 3=12 (м) - столько было ткани; 2) 12 : 2=6 (к) - столько кофт можно сшить из 12 м ткани.
Решить задачу алгебраическим методом - это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений. Если для одной и той же задачи можно составить различные уравнения, то это означает, что данную задачу можно решить различными алгебраическими способами.
Задача. Свитер, шапку и шарф связали из 1 кг 200 г шерсти. На шарф потребовалась на 100 г больше, чем на шапку, и на 400 г меньше, чем на свитер. Сколько грамм шерсти израсходовали на каждую вещь? Эту задачу можно решить тремя различными способами.
1 способ: Обозначим через х (г) массу шерсти, израсходованной на шапку. Тогда на шарф будет израсходовано (х +100) г, а на свитер ((х + 100) + 400) г. Так как на все три вещи израсходовано 1 200 г, то можно составить уравнение. х+(х+100)+((х+100)+400)=1 200 Выполнив преобразования, получим, что х = 200. Таким образом, на шапку было израсходовано 200 г, на шарф - 300 г, так как 200 + 100 = 300, на свитер - 700 г.
2 способ Обозначим через х (г) массу шерсти, израсходованной на шарф. Тогда на шапку будет израсходовано (х - 100) г, а на свитер - (х + 400) г. Поскольку на все три вещи израсходовано 1 200 г, то можно составить уравнение: х + (х - 100) + (х + 400) = 1 200
3 способ Обозначим через х (г) массу шерсти, израсходованной на свитер. Тогда на шарф будет израсходовано (х - 400) г, а на шапку - (х- 400-100) г. Поскольку на все три вещи израсходовано 1 200 г, то можно составить уравнение; х+(х-400) +(х-400-100)=1 200 Выполнив преобразования, получим, что х=700. Таким образом, если на свитер израсходовано 700 г, то на шарф пошло 300 г, а на шапку - 200 г (700-400-100=200).
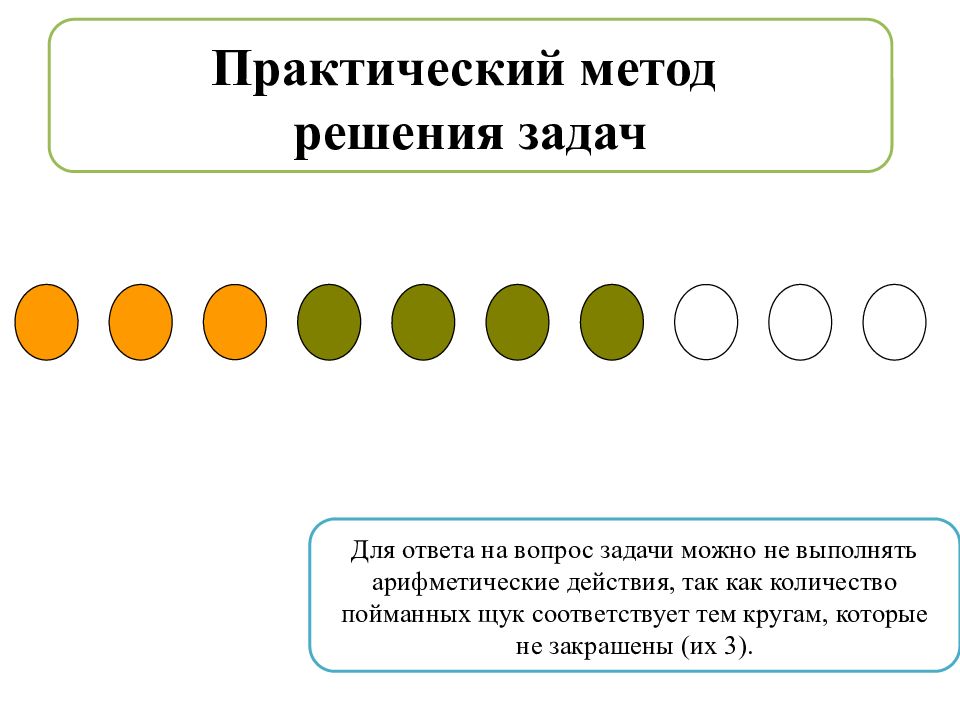
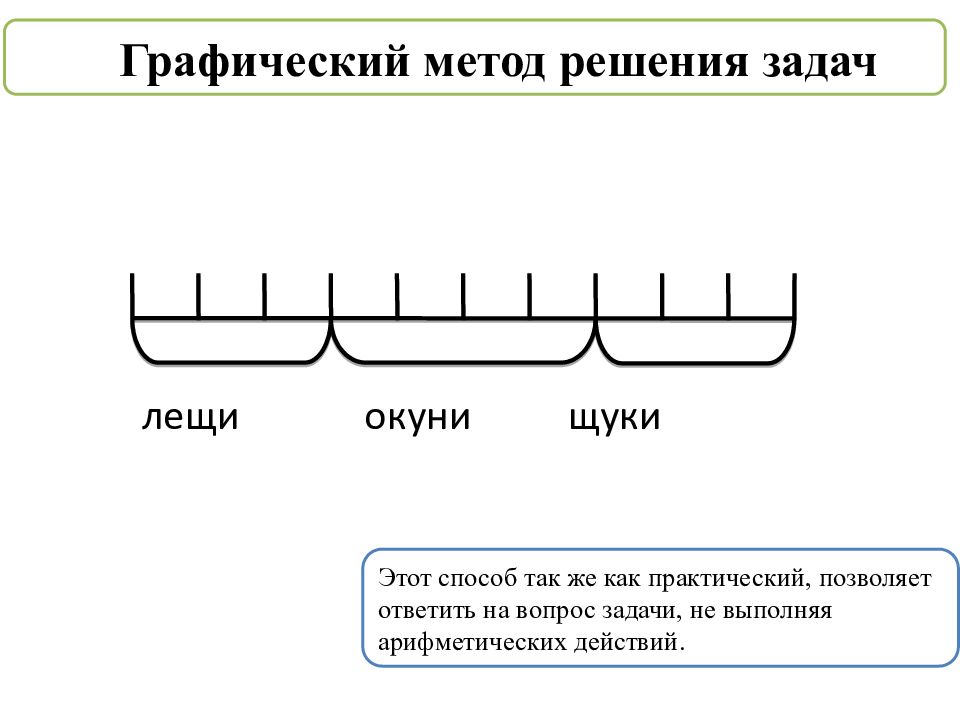
Задача. Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак? Кроме арифметического и алгебраического методов решения задач существуют еще практический и графический.
Практический метод решения задач Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не закрашены (их 3).
Графический метод решения задач Этот способ так же как практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий. лещи окуни щуки
