Первый слайд презентации: Текстовые задачи
Слайд 2
План Структура текстовой задачи. Методы и способы решения задач. Этапы решения задач. анализ задачи; поиск и составление плана решения; осуществление плана решения; проверка плана решения. 4.Моделирование в процессе решения задачи.
Слайд 4: Содержание
Текстовая задача есть описание на естественном языке некоторого явления (ситуации, процесса) с требованием дать количественную характеристику какого-либо компонента этого явления, установить наличие или отсутствие некоторого отношения между компонентами или определить вид этого отношения.
Слайд 5: Роль текстовой задачи
Формирование многих математических понятий. Формирование умений строить математические модели реальных явлений. Развитие логического мышления.
Слайд 6
Задача Условие Требование Условия задачи - количественные или качественные характеристики объектов задачи и отношений между ними. Требования задачи могут быть сформулированы в вопросительной и утвердительной форме.
Слайд 7
Условия и требования взаимосвязаны. Систему взаимосвязанных условий и требований называют высказывательной моделью задачи
Слайд 8
Величину, значения которой требуется найти, называют искомой величиной, а числовые значения искомых величин - искомыми, или неизвестными.
Слайд 9
Для определения структуры текстовой задачи рассмотрим пример Задача. Для украшения елки дети вырезали 42 снежинки, а фонариков на 18 меньше, шаров на 6 больше, чем фонариков. Сколько всего игрушек сделали дети?
Слайд 10
Объекты задачи: снежинки, фонарики, шары. Условия: 42 снежинки. Фонариков на 18 меньше, чем снежинок. Шаров на 6 больше, чем фонариков. Требования: 1. Сколько сделано снежинок? 2. Сколько сделано фонариков? 3. Сколько сделано шаров?
Слайд 11: По отношению между условиями и требованиями различают:
Определенные задачи : условий столько, сколько необходимо и достаточно для выполнения требований; Недоопределенные задачи : условий недостаточно для получения ответа (недостающие данные); Переопределенные задачи : в них имеются лишние условия ( избыточные данные)
Слайд 12
Т.о. Решением задачи называют: Результат, т. е. ответ на требование задачи; Процесс нахождения этого результата.
Арифметический Алгебраический
Слайд 15
Арифметический метод : ответ на требование задачи находится посредством выполнения арифметических действий над числами; Одну и ту же задачу можно решить различными арифметическими способами.
Слайд 16: Задача
«За 8 часов рабочий изготавливает 96 одинаковых деталей. Сколько деталей он изготовит за 5 часов?» 1 способ: 1. 96 : 8 = 12(д/ч) 2. 12 · 5 = 60(дет.) 2 способ: 1. 8 : 5 = 1,6(раза) 2. 96 : 1,6 = 60(дет.) 3 способ: 1. 8ч. = 480мин. 2. 480 : 96 = 5(мин.) 3. 5ч. = 300мин. 4. 300 : 5 = 60(дет.)
Слайд 17
Алгебраический метод : ответ на требование задачи находится путем составления и решения уравнения или системы уравнений. Одну и ту же задачу можно решить различными алгебраическими способами.
Слайд 18: Задача
«Кофейник и 2 чашки вмещают 740 гр. воды. В кофейник входит на 380 гр. больше, чем в чашку. Сколько грамм вмещает кофейник ?» 1 способ: Пусть x грамм воды вмещает чашка, поэтому кофейник = x + 380гр. 2 x + ( x + 380) = 740; 3 x = 360; X = 120 (гр.); 120 + 380 = 500 (гр.)- вмещает кофейник 2 способ: Пусть x грамм воды вмещает кофейник, поэтому вместимость чашки x – 380гр. 2 ( x – 380) + x = 740; 3 x = 740 + 760; 3 x = 1500; X = 500 (гр.)-вмещает кофейник 3 способ: Пусть x грамм воды вмещает чашка, кофейник y. 2 x + y = 740; x - y = 380 3 x = 360; X = 120 (гр.) -вмещает чашка 120*2 = 240 740 – 240 = 500 (гр.)-вмещает кофейник
Слайд 20: Решение задачи арифметическим методом включает основные этапы:
Анализ задачи. Поиск плана решения. Осуществление плана решения. Проверка решения.
Слайд 21: 1. Анализ задачи
Назначение этапа: понять в целом ситуацию, описанную в задаче; выделить условие и требования; назвать известные и искомые объекты, выделить отношения между ними. С этой целью задаются вопросы: О чем задача? Что требуется найти? Что обозначают те или иные слова? Что неизвестно? Что является искомым?
Слайд 22
Осмыслить задачу поможет другой прием - перефразировка текста задачи: замена данного в задаче описания ситуации другим, сохраняющим все отношения, но более явно их выражающих. Это достигается отбрасыванием несущественной (излишней) информации, замены описания некоторых понятий терминами и наоборот.
Слайд 23
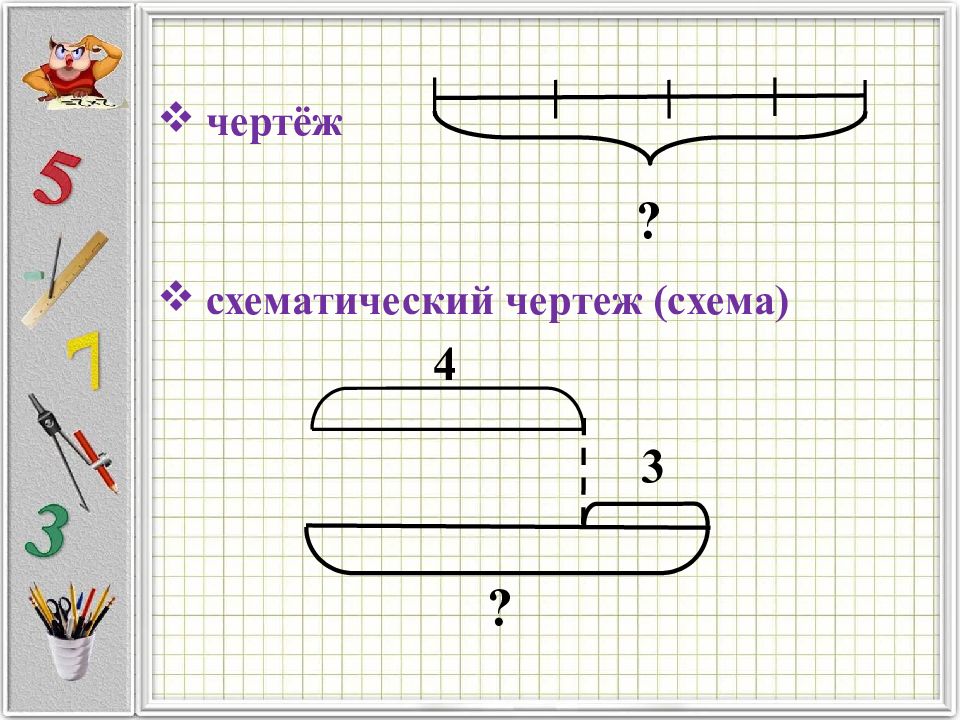
Итогом анализа задачи является составление вспомогательной модели (может быть в виде таблицы, схематического чертежа). После построения вспомогательной модели необходимо проверить: Все ли объекты показаны на модели; Все ли отношения отражены; Все ли числовые данные приведены; Есть ли вопрос (требование) и правильно ли он указывает искомое.
Слайд 24: 2. Поиск и составление плана решения задачи
Назначение этапа: Установить связь между данными и исходными объектами Наметить последовательность действий План решения задачи – это идея решения, его замысел. План решения может оказаться неверной, тогда вновь возвращаются к анализу задачи и начинают все сначала.
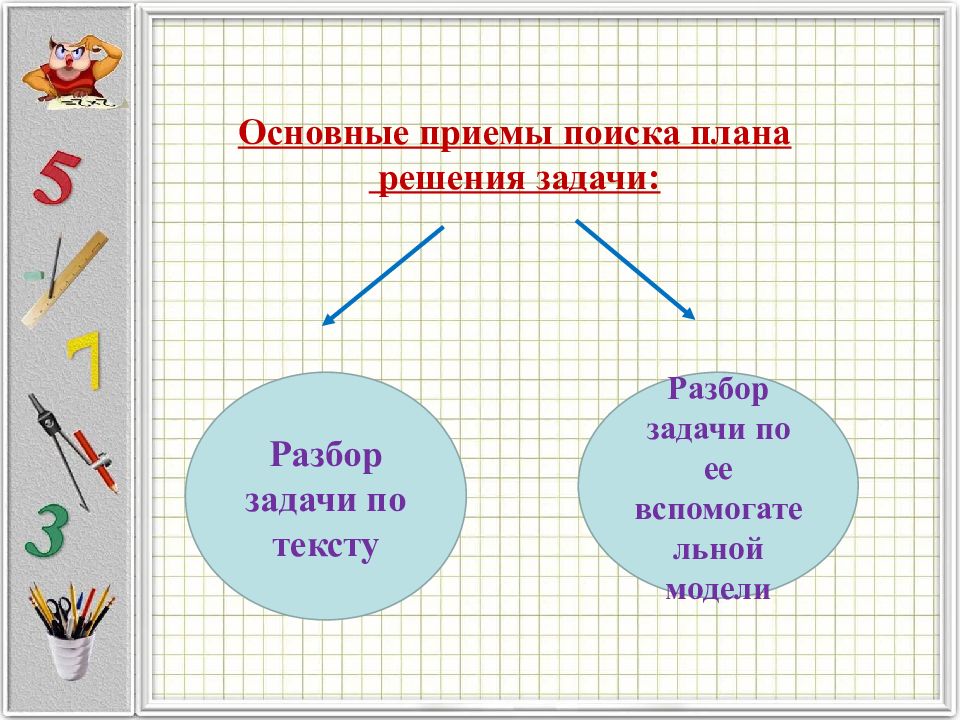
Слайд 25: Основные приемы поиска плана решения задачи:
Разбор задачи по тексту Разбор задачи по ее вспомогательной модел и
Слайд 26
Синтетическим методом: цепочка рассуждений строится от данных к искомому. Выделяются два данных, а на основе связи между ними определяется какое неизвестное можно найти и с помощью каких арифметических действий и т. д. Разбор задачи по тексту проводится:
Слайд 27
Аналитический метод : цепочка рассуждений строится от искомого к данным. Обращают внимание на вопрос и устанавливают, что достаточно знать для ответа на вопрос и т.д. Этап завершается составлением плана решения задачи (устно или письменно).
Слайд 28: 3. Осуществление плана решения
Назначение этапа: найти ответ на требование задачи, выполнив все действия в соответствии с планом. Используются следующие приемы: Запись по действиям : С пояснением: 42-18=24 (шт.) - сделали фонариков Без пояснения: 42-18=24 (шт.) С вопросом: Сколько фонариков сделали дети? 42-18=24 (шт.) Запись решения в виде выражения: 42+ (42-18) + (42-18) + 6= 96 (шт.)
Слайд 29
4. Проверка решения задачи Назначение этапа : установить правильность или ошибочность решения задачи. Приемы проверки решения задачи: Прикидка результата (установление границ ответа). Чаще выполняется до начала решения. Она не дает полного представления о правильности решения, но помогает избежать абсурдных результатов.
Слайд 30
Установление соответствия между результатом и условиями. Найденный результат вводится в тексты задачи и устанавливается не возникает ли противоречий. При этом проверяются все отношения. Если противоречий нет, то задача решена верно. Решение задачи другим способом. Если решение задачи другим способом приводит к тому же результату, то делается вывод о том, что задача решена верно. Если задача решена арифметическим способом, то правильность решения можно проверить, решив задачу алгебраическим способом и наоборот.
Слайд 32
Математическая модель – это описание какого-либо реального процесса на языке математических понятий, формул и отношений. Математической моделью текстовой задачи является: выражение (если задача решается арифметическим методом ) уравнение (если задача решается алгебраическим методом)
Слайд 33
Прием моделирования заключается в том, что для исследования объекта (текстовой задачи) выбирают другой объект, который исследуют, а результаты изученного объекта переносят на первоначальный объект.
Слайд 34
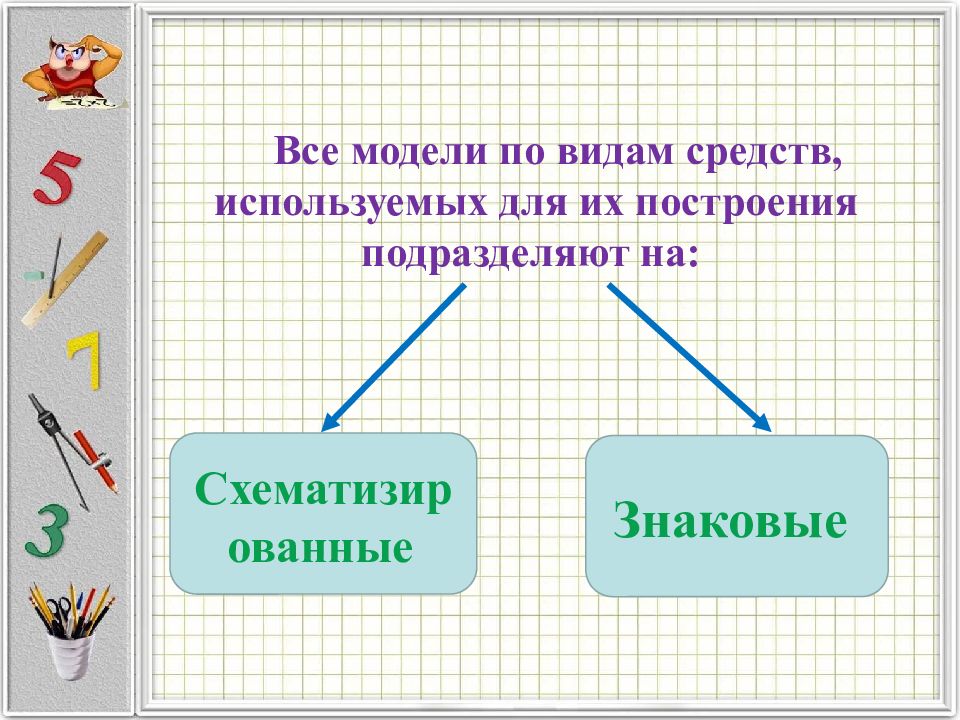
Все модели по видам средств, используемых для их построения подразделяют на: Схематизированные Знаковые
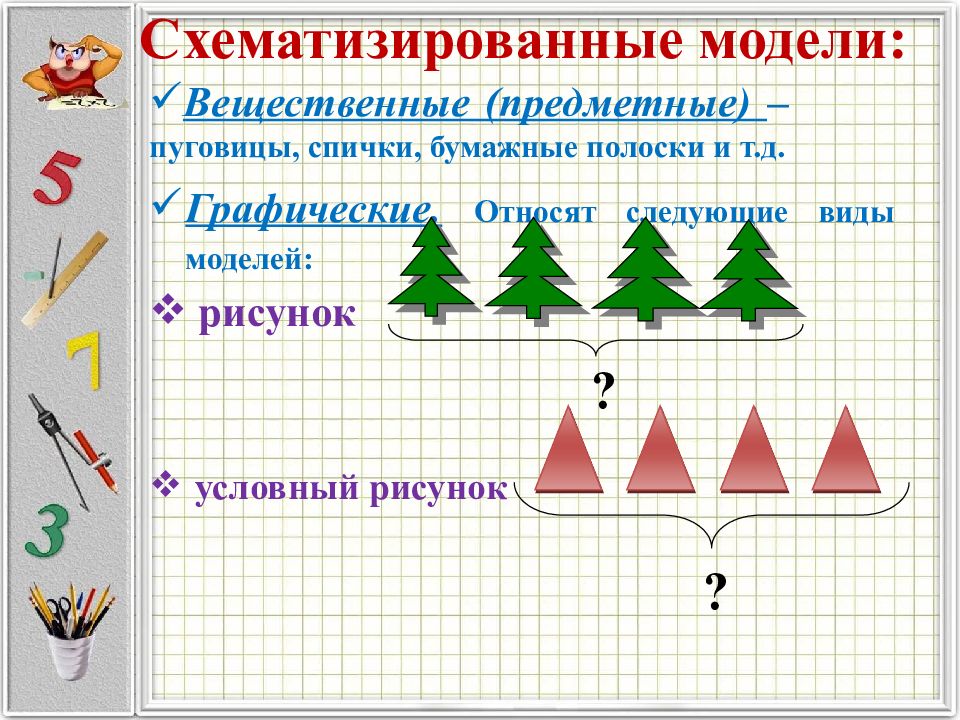
Слайд 35: Схематизированные модели:
Вещественные (предметные) – пуговицы, спички, бумажные полоски и т.д. Графические. Относят следующие виды моделей: рисунок условный рисунок ? ?
Слайд 37: Знаковые модели:
выражения, уравнения ( выполнены на математическом языке); таблица (выполнена на естественном языке): Цена Количество Стоимость Ложки Вилки ? одинаковая ? 5 шт. 3 шт. 10 руб. ? краткая запись (выполнены на естественном языке): 1 класс – 18 уч. 2 класс – ? на 6 уч. > ? уч.
Последний слайд презентации: Текстовые задачи
Модели, выполненные на математическом языке называются решающими моделями Модели, выполненные на естественном языке называются вспомогательными моделями. Т.о. Модель – это копия задачи, поэтому на ней должны быть представлены все ее объекты, все отношения между ними, указаны требования.