Первый слайд презентации: Тема урока:
Применение определенного интеграла для нахождения площади криволинейной трапеции
Слайд 2
ПОВТОРИМ! 1. Функция F (х) называется первообразной функции f(x) на некотором промежутке, если для всех Х из этого промежутка выполняется равенство: 2. F(x)+C, где С произвольная постоянная (любое число), называется семейством первообразных. Другими словами нахождение первообразной – это обратное действие нахождения производной. 3. Совокупность всех первообразных данной функции f(x) называется неопределённым интегралом и обозначается:
Слайд 7
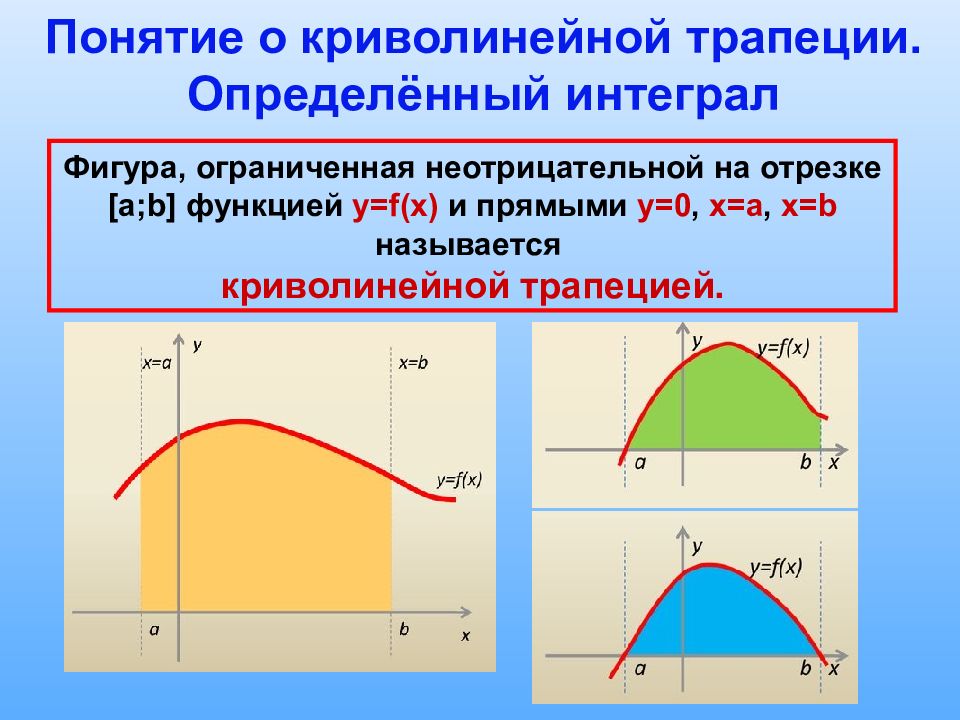
Понятие о криволинейной трапеции. Определённый интеграл Фигура, ограниченная неотрицательной на отрезке [a;b] функцией y=f(x) и прямыми у=0, x=a, x=b называется криволинейной трапецией.
Слайд 8
Площадь криволинейной трапеции можно вычислить по формуле: Где F(x) – первообразная функции y=f(x) Вычисление площади криволинейной трапеции сводится к отысканию первообразной F(x) функции f(x), то есть к интегрированию функции f(x). Определение Разность F(b)–F(a) называют интегралом от функции f(x) на отрезке [a;b] и обозначают: Подынтегральная функция Подынтегральное выражение Верхний предел интегрирования Нижний предел интегрирования
Слайд 9
Формула Ньютона - Лейбница Исаак Ньютон 1642-1727 Готфрид Лейбниц 1646-1716 гг. Таким образом:
Слайд 10
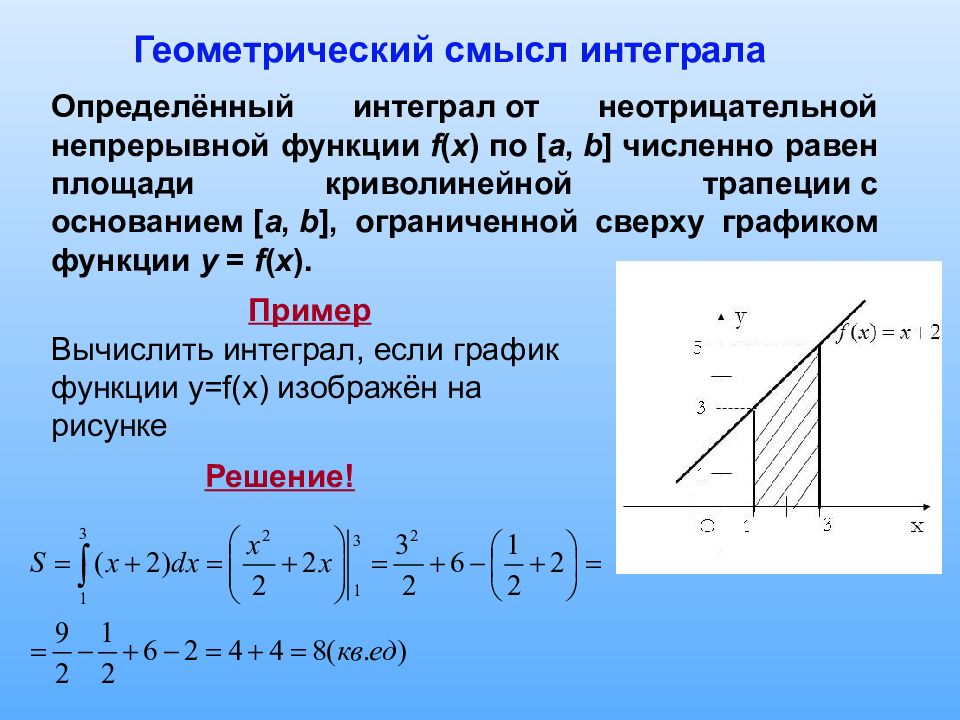
Геометрический смысл интеграла Определённый интеграл от неотрицательной непрерывной функции f ( x ) по [ a, b ] численно равен площади криволинейной трапеции с основанием [ a, b ], ограниченной сверху графиком функции y = f ( x ). Пример Вычислить интеграл, если график функции y=f(x) изображён на рисунке Решение!
Слайд 11
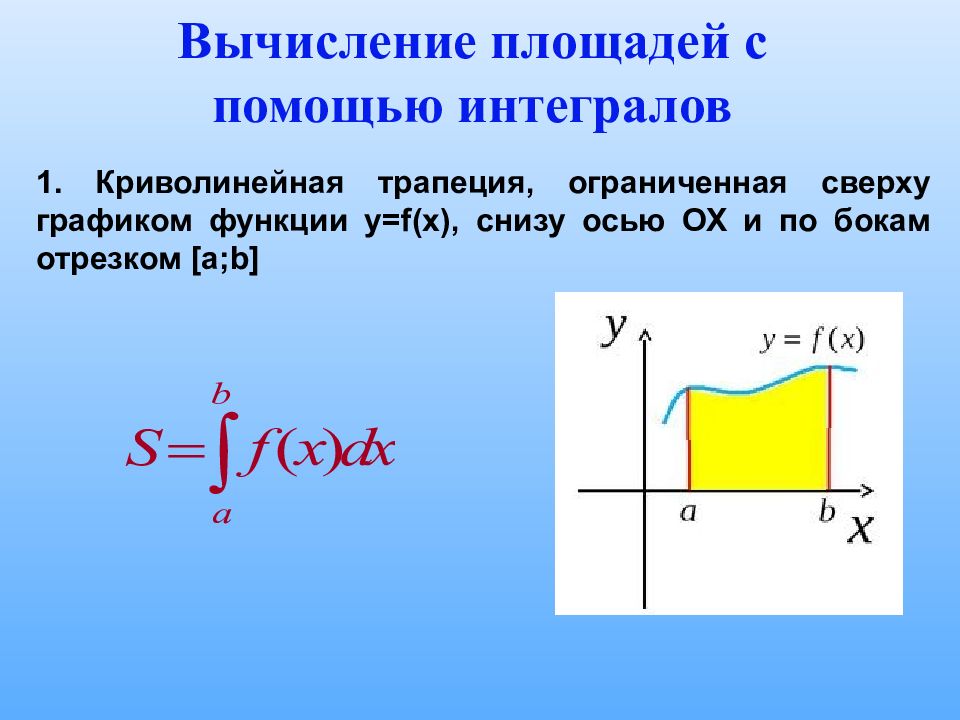
Вычисление площадей с помощью интегралов 1. Криволинейная трапеция, ограниченная сверху графиком функции y=f(x), снизу осью ОХ и по бокам отрезком [a;b]
Слайд 12
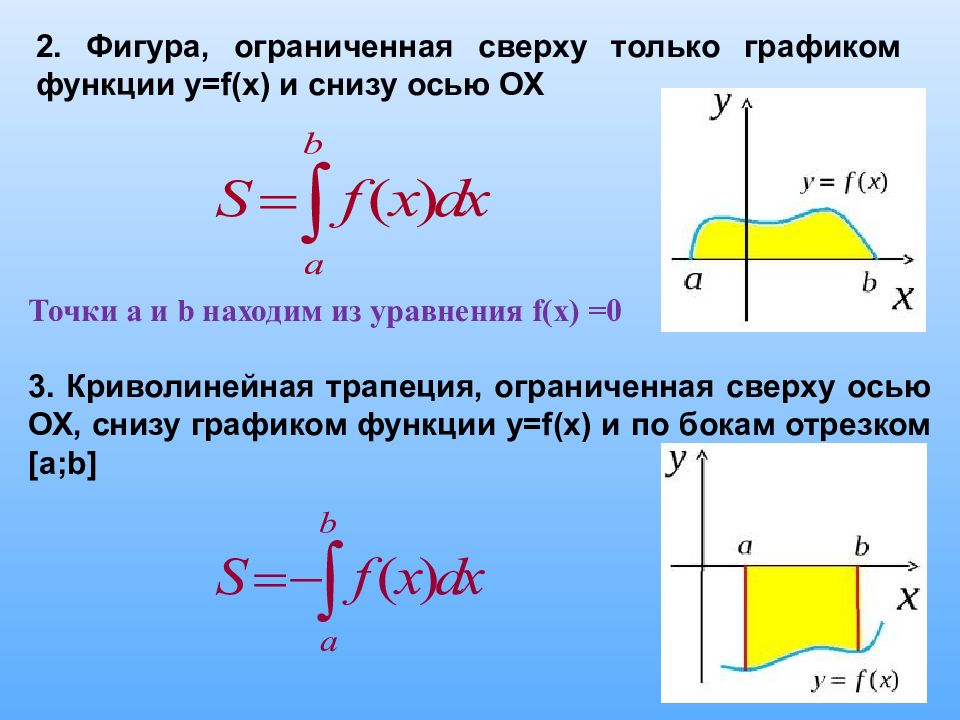
2. Фигура, ограниченная сверху только графиком функции y=f(x) и снизу осью ОХ Точки а и b находим из уравнения f(x) =0 3. Криволинейная трапеция, ограниченная сверху осью ОХ, снизу графиком функции y=f(x) и по бокам отрезком [a;b]
Слайд 13
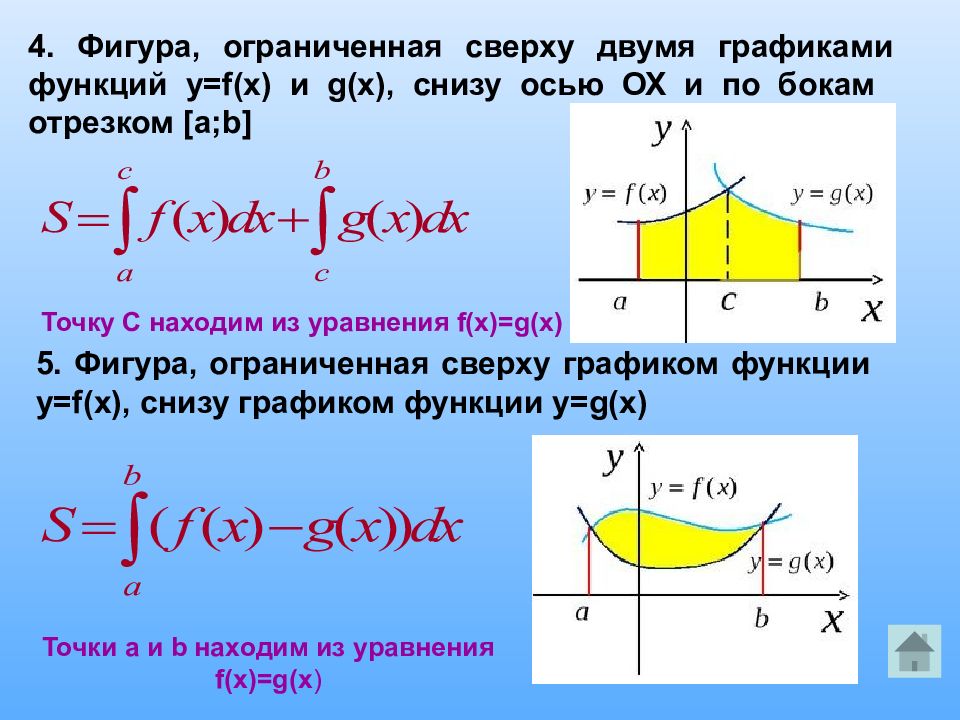
4. Фигура, ограниченная сверху двумя графиками функций y=f(x) и g(x), снизу осью ОХ и по бокам отрезком [a;b] Точку С находим из уравнения f(x)=g(x) 5. Фигура, ограниченная сверху графиком функции y=f(x), снизу графиком функции y=g(x) Точки a и b находим из уравнения f(x)=g(x )
Слайд 14
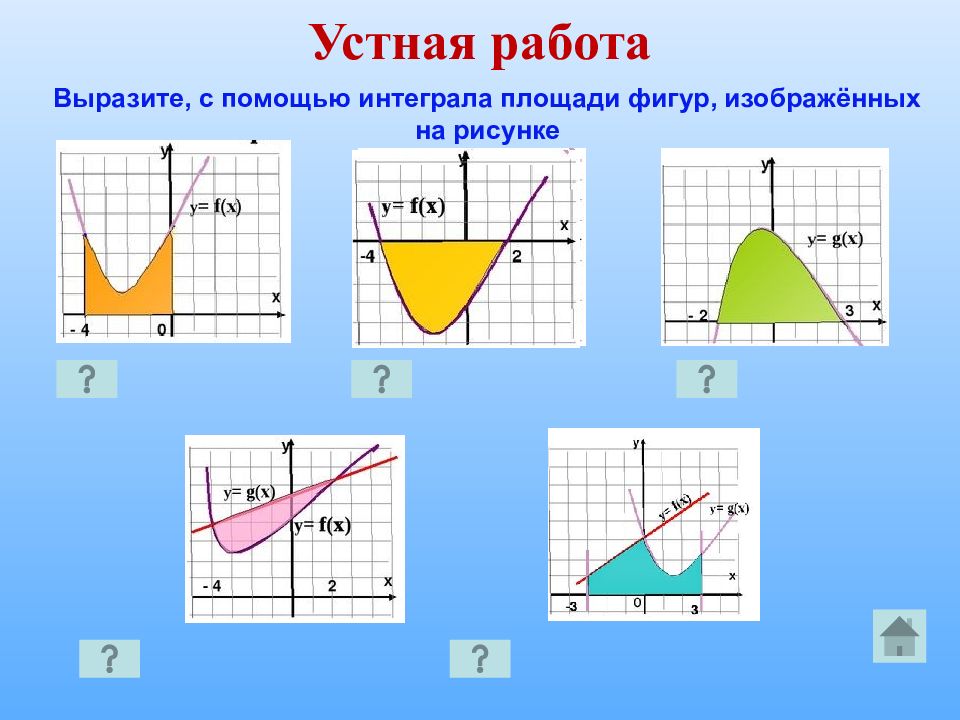
Устная работа Выразите, с помощью интеграла площади фигур, изображённых на рисунке
Слайд 15
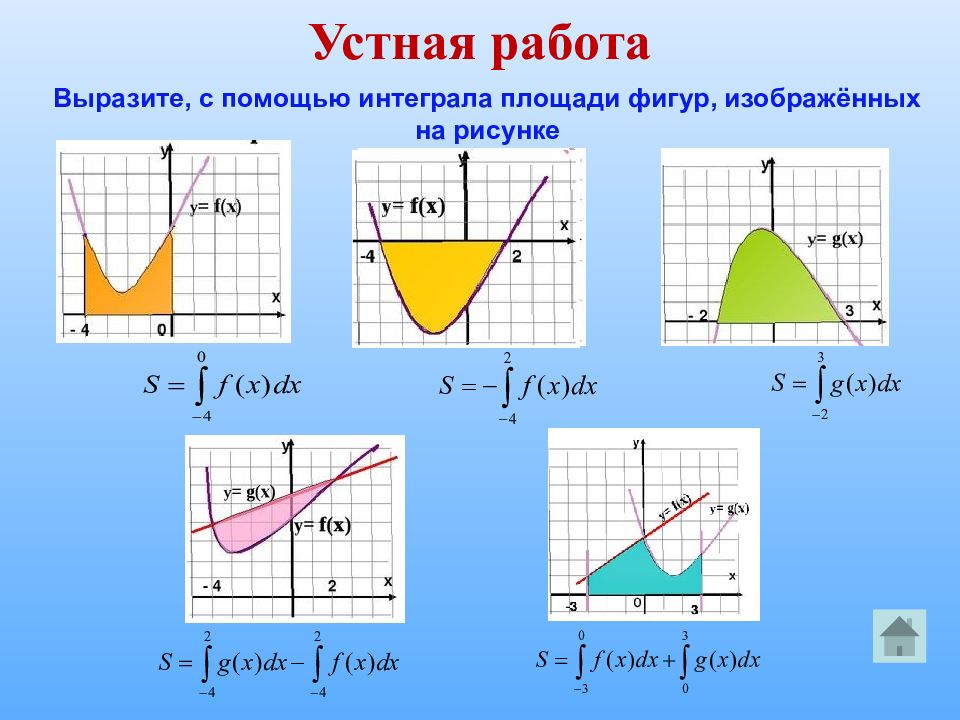
Устная работа Выразите, с помощью интеграла площади фигур, изображённых на рисунке
Слайд 16
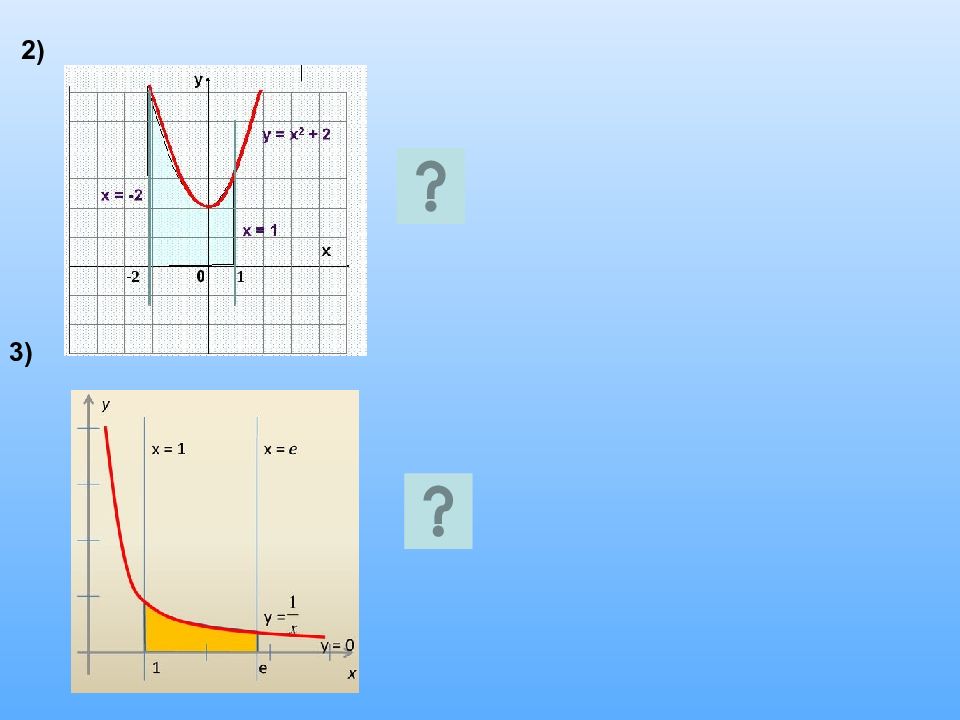
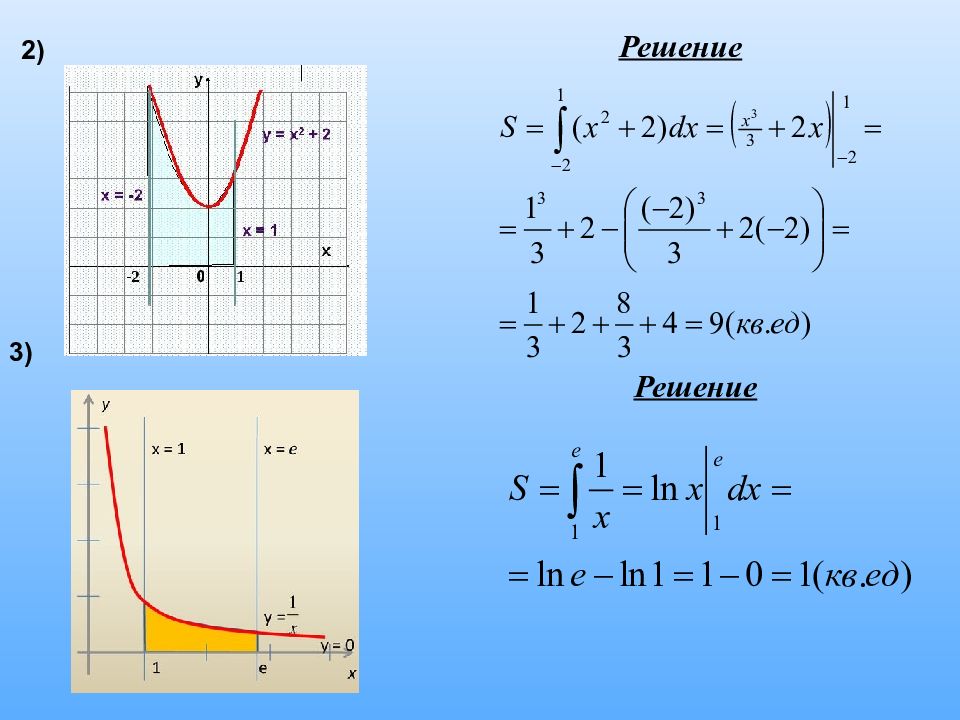
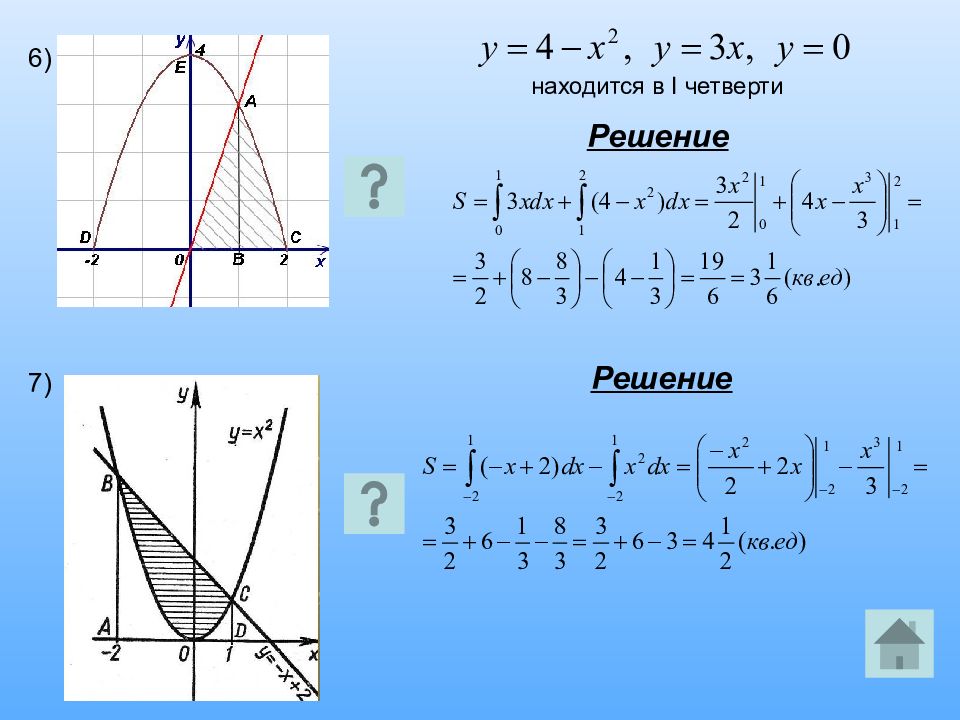
Решение задач Задание №1 Найти площадь криволинейной трапеции, изображённой на рисунках Используя формулу: Решение Получаем: 1)
Слайд 23
Программируемый контроль Задания Ответы Вычислить площадь фигуры, ограниченной линиями 1 Вариант 2 Вариант 1 2 3 4 y=x 2 +2, y=x+2 y= -x 2 +4, y= -x+4 7 1/6 2/3 1/3 y=sin 2x, y=0, x=0, x= π/4 y=cos 2x, y=0, x= - π / 4, x= π /4 2 -1 1/2 1 y= -2/x, y=2, x= -4, x= -1 y= -1/x, y=1, x= -3, x= -1 6-4ln2 2-ln3 2ln2 2-3ln2 ЗАДАНИЕ №1
Слайд 24
Программируемый контроль Задания Ответы Вычислить площадь фигуры, ограниченной линиями 1 Вариант 2 Вариант 1 2 3 4 y=x 2 +2, y=x+2 y= -x 2 +4, y= -x+4 7 1/6 2/3 1/3 y=sin 2x, y=0, x=0, x= π/4 y=cos 2x, y=0, x= - π / 4, x= π /4 2 -1 1/2 1 y= -2/x, y=2, x= -4, x= -1 y= -1/x, y=1, x= -3, x= -1 6-4ln2 2-ln3 2ln2 2-3ln2 Правильные ответы 1 Вариант : 2.3,1 2 Вариант: 2,4,2 ЗАДАНИЕ №1
Слайд 25
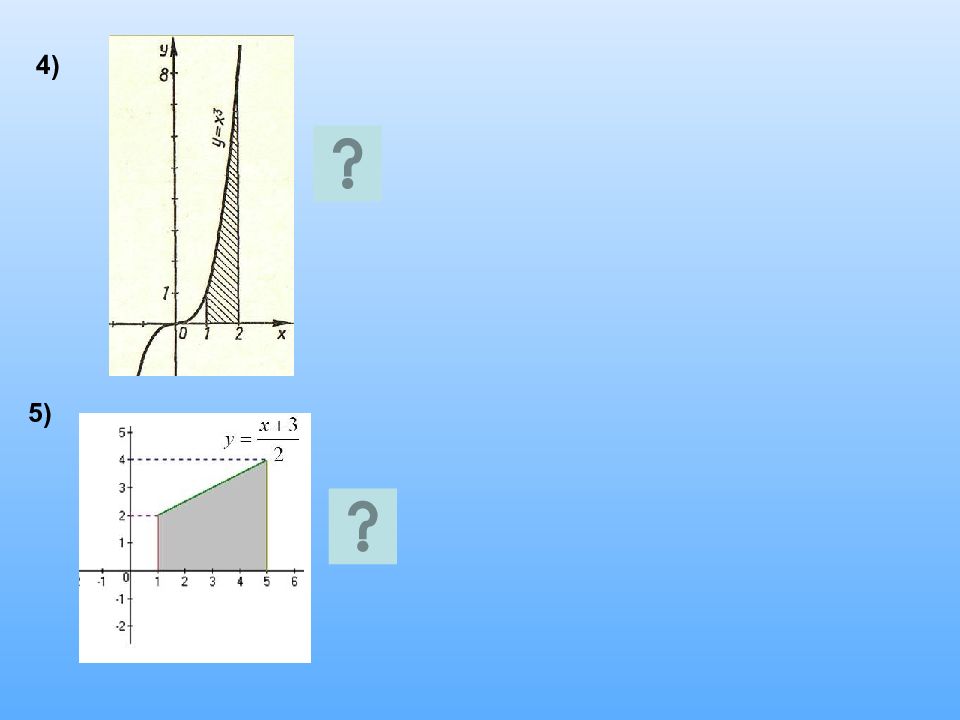
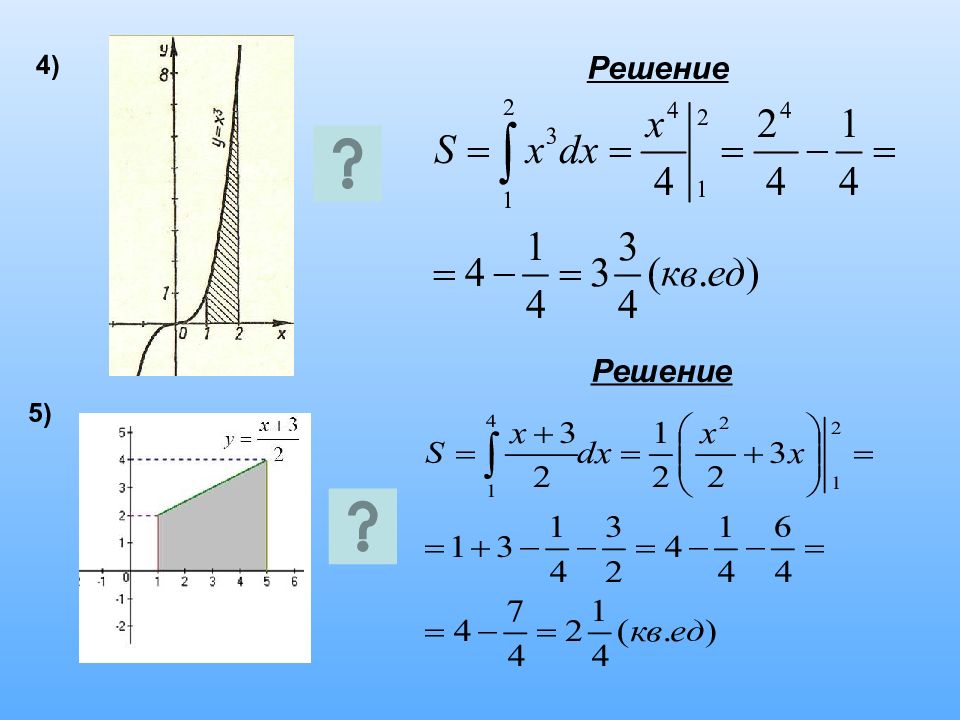
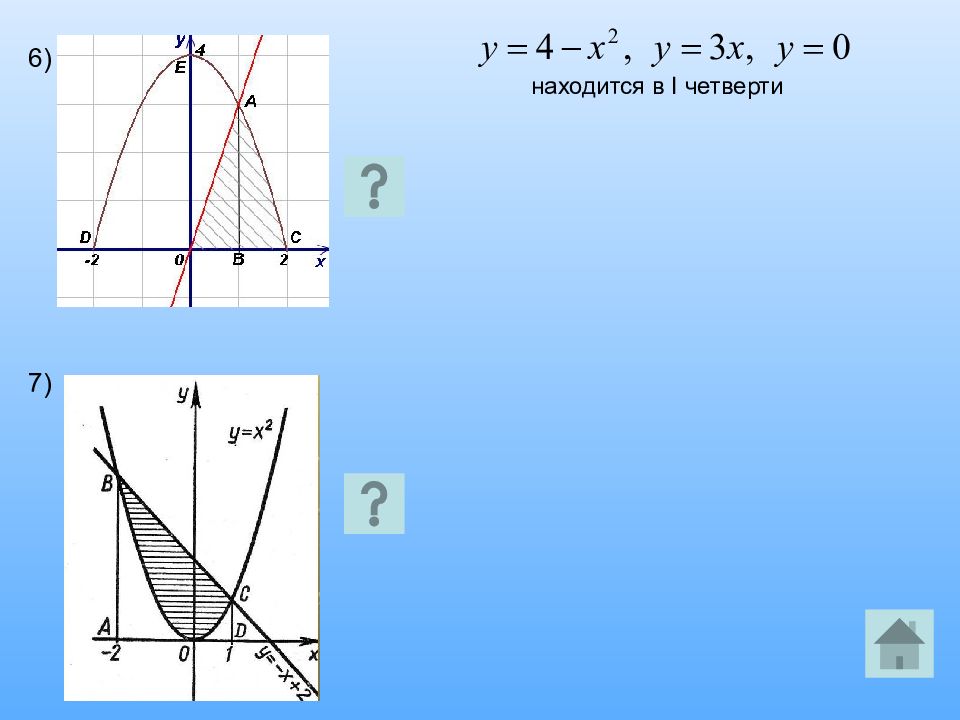
Вычислите площадь фигуры, ограниченной линиями (схематично изобразив графики функций). Ответ: 1) 4,5 2) 9/8 3) 4,5 4)1/3 ЗАДАНИЕ №2 Вычислить площадь фигуры, ограниченной линиями и осью ОХ, если ЗАДАНИЕ № 3
Слайд 26
Контрольные вопросы: Какая функция называется первообразной для функции f(x) ? Чем отличаются друг от друга различные первообразные функции для данной функции f(x) ? Дайте определение неопределённого интеграла. Как проверить результат Какое действие называется интегрированием? интегрирования? Дайте определение определённого интеграла. Сформулируйте теорему Ньютона-Лейбница. Перечислите свойства интеграла. Как вычислить площадь плоской фигуры с помощью интеграла (составьте словесный алгоритм)? Перечислите области применения интеграла, назовите величины, которые можно вычислить с помощью интеграла.