Слайд 2
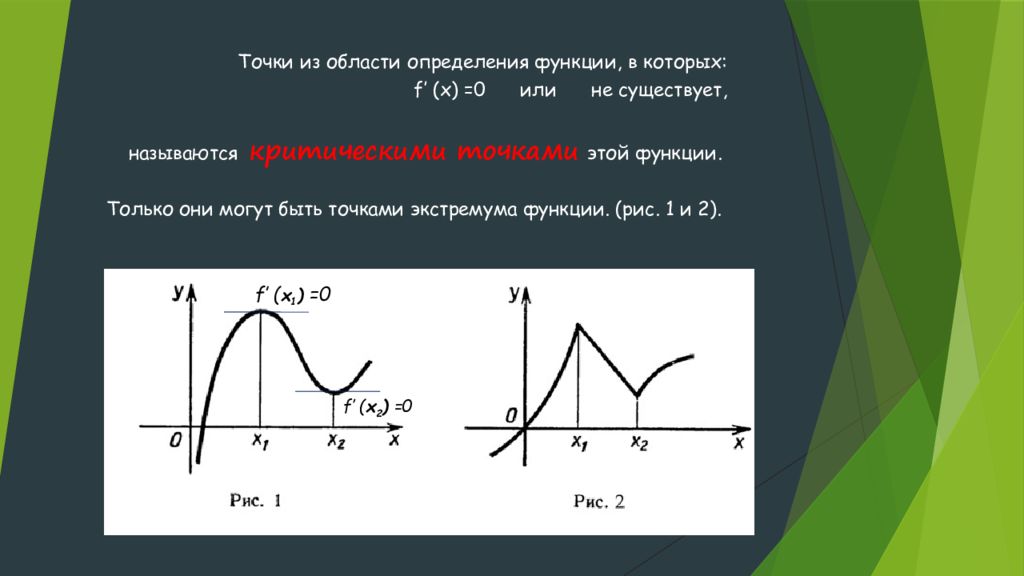
Точки из области определения функции, в которых: f′ (x) =0 или не существует, называются критическими точками этой функции. Только они могут быть точками экстремума функции. (рис. 1 и 2). f′ ( x 1 ) =0 f′ ( x 2 ) =0
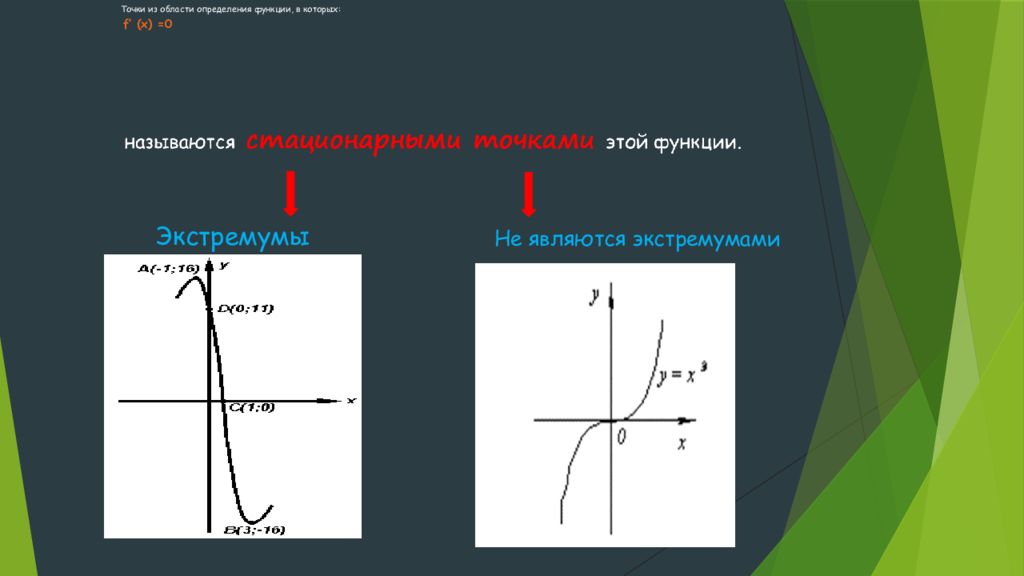
Слайд 3: Точки из области определения функции, в которых: f′ (x) =0
Экстремумы Не являются экстремумами
Слайд 4
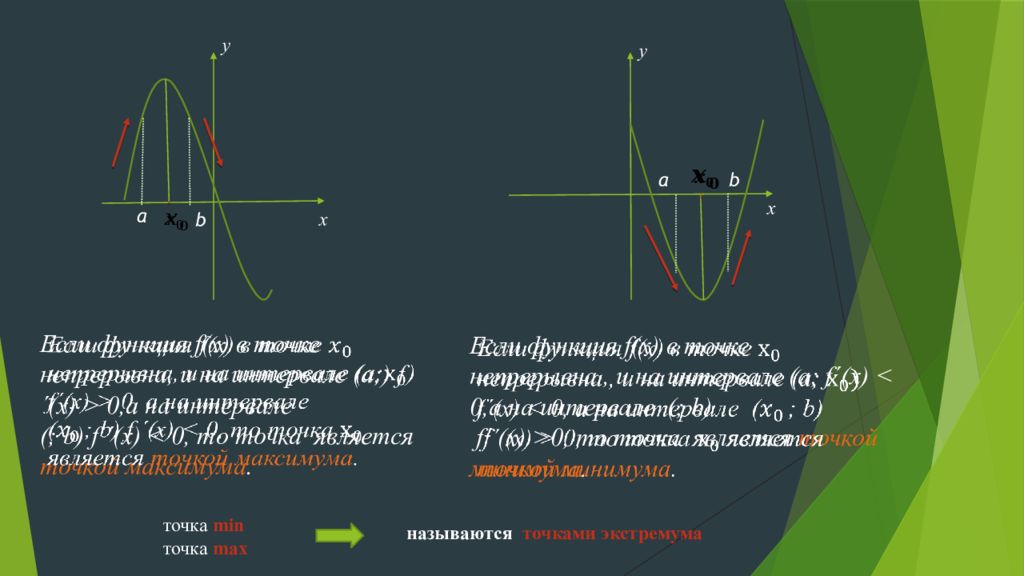
y x y x Если функция f(x) в точке непрерывна, и на интервале ( a ; ) f´(x ) > 0, а на интервале ( ; b) f ˊ(x ) < 0, то точка является точкой максимума. Если функция f(x) в точке непрерывна, и на интервале (а; f´(x ) < 0, а на интервале ( ; b ) fˊ (x) > 0, то точка является точкой минимума. a a b b называются точками экстремума точка min точка max
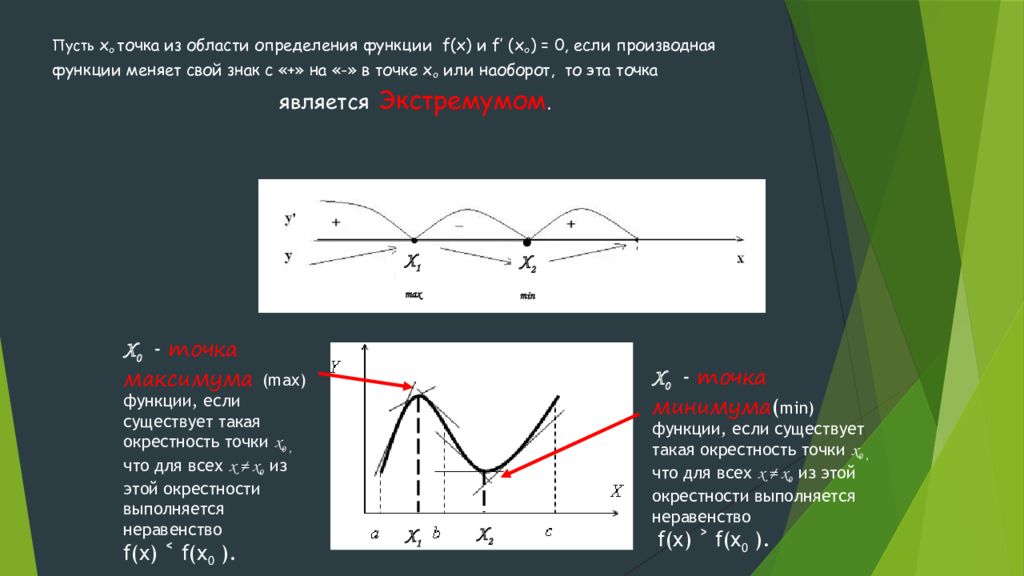
Слайд 5: Пусть x о точка из области определения функции f(x) и f′ (x о ) = 0, если производная функции меняет свой знак с «+» на «-» в точке x о или наоборот, то эта точка
является Экстремумом. Х 1 Х 2 Х 1 max Х 2 min Х 0 - точка максимума ( max) функции, если существует такая окрестность точки х 0, что для всех х ≠ х 0 из этой окрестности выполняется неравенство f(x) ˂ f(x 0 ). Х 0 - точка минимума ( min) функции, если существует такая окрестность точки х 0, что для всех х ≠ х 0 из этой окрестности выполняется неравенство f(x) ˃ f(x 0 ).
Слайд 6: Алгоритм поиска точек экстремума функции:
н айти производную функции; р ешить уравнение f‘ (x) = 0, найти критические точки с помощью метода интервалов определить знаки производной в окрестностях критических точек; и спользуя достаточное условие существовани я экстремума, найти точки максимума и минимум а
Слайд 7
- 1. Точка перегиба Пример № 2. Дана функция f(x) = - 1. Решение: f ˊ(x) = f ˊ(x) = 0, 3 = 0 или x = 0. f ˊ( 0 ) =3· 0 = 0, но экстремума в этой точке функция не имеет. Пример №1. Дана функция y = 3x + 2 Решение. yˊ = (3x + 2) ´ = 3 – критических точек нет у = k х+ b - прямая y x 0 + +
Слайд 8
Пример № 3. Дана функция f(x) = - 2 f´(x) = - 4x, - 4x = 0, 4x ( - 1) = 0, 4 x(x -1) (x +1) = 0 4x = 0, x – 1 = 0, x + 1 = 0 x = 0 x = 1 x = - 1 -1 ; 0; 1 – критичес. точки - 1 0 1 - + - + f ˊ(-2) = 4 · (-2) (-2 -1) (-2+1 ) = - 24 < 0 f ˊ ( ) = 4 · ( -1) ( + 1) < 0 f ˊ (- ) = 4 · ( - -1) (- +1) > 0 f ˊ (2 ) = 4 · (2 ) (2 -1) (2+1 ) > 0 - 1 1 0 min max min = 0, = - 1 ; 1.
Слайд 9
1 + - + Пример №4. Определим точки экстремума функции f (x) = 2 - - 4x + 5 Решение. y - - 4x + 5)ˊ = 6 - 2x – 4 = 2 ( - x – 2 ) ; f '( x) = 0 2 ( - x – 2) = 0, - x – 2 = 0, = 1, = - 1 ; - - крит. точки 3) на числовой прямой отметим = 1, = -, и определим знак производной на каждом интервале. 4 ) в окрестности точки x = - производная меняет знак с плюса на минус, а в окрестности точки х = 1 производная меняет знак с минуса на плюс. Пользуясь условием экстремума, получаем, что точка x = - - это точка максимума, а x = 1 – точка минимума. = -, = 1 f ˊ(0) = 3 · - 0 – 2 = - 4 < 0, f ˊ ( -1 ) = 3· - (-1) – 2 = 2 > 0 f ˊ (2) = 3· - 2 – 2 = 8 > 0