Определение « Математическая грамотность – это способность индивидуума проводить математические рассуждения и формулировать, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира. Она включает использование математических понятий, процедур, фактов и инструментов, чтобы описать, объяснить и предсказать явления. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые необходимы конструктивному, активному и размышляющему гражданину.»
Механизм взаимодействия двух миров Рассуждать
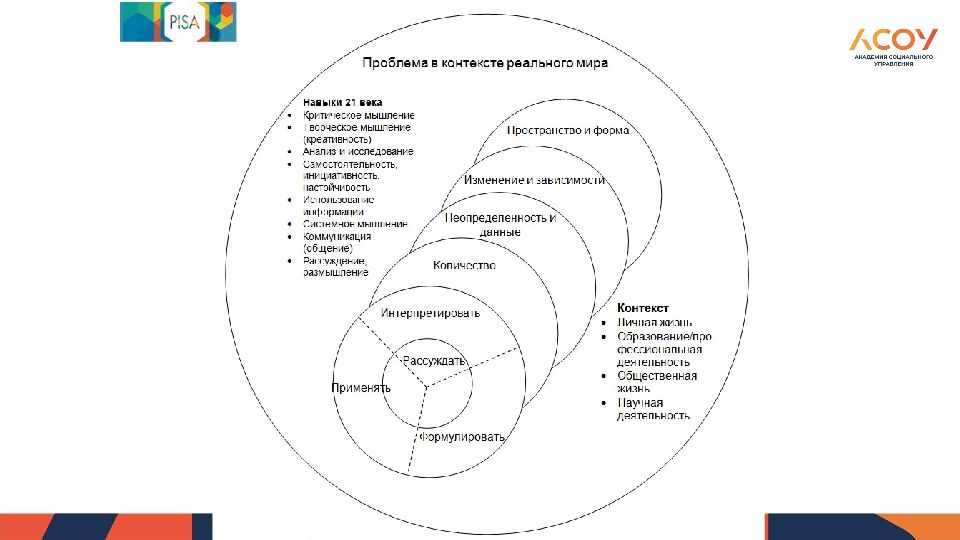
Структура оценки математической грамотности Математическое содержание, которое используется в тестовых заданиях (предметное ядро функциональной грамотности) Когнитивные процессы (составляющие интеллектуальной деятельности), которые описывают, что делает ученик, чтобы связать контекст, в котором представлена проблема, с математикой, необходимой для её решения Контекст, в котором представлена проблема.
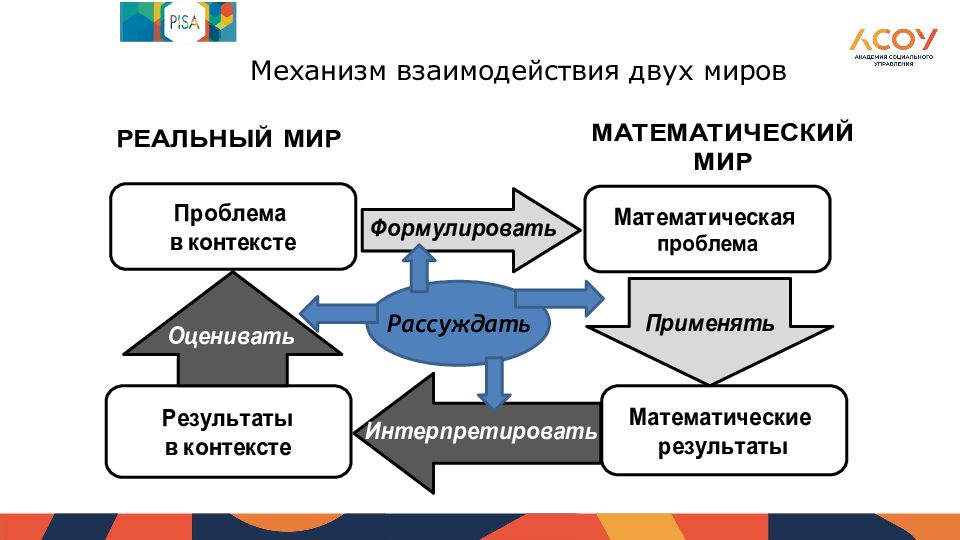
Особое внимание к оценке математических рассуждений. Новая точка зрения на связь между математическими рассуждениями и решением поставленной проблемы: Для решения проблемы математически грамотный учащийся сначала должен увидеть математическую природу проблемы, представленной в контексте реального мира, и сформулировать ее на языке математики. Это преобразование требует математических рассуждений и, возможно, является центральным компонентом того, что значит быть математически грамотным. Это один из навыков XXI века. Компьютерное моделирование
Когнитивные процессы Для описания интеллектуальной деятельности при решении проблем используются следующие ее составляющие: формулировать ситуацию математически - 25% применять математические понятия, факты, процедуры – 25% интерпретировать, использовать и оценивать математические результаты - 25% рассуждать – 25%
Формулировать ситуации математически ( formulating situations mathematically ) способность распознавать и выявлять возможности использовать математику, а затем трансформировать проблему, представленную в контексте реального мира, в математическую структуру В процессе формулирования проблемы на математическом языке учащиеся определяют, из какого раздела курса они могут извлечь необходимые математические знания, чтобы проанализировать, спланировать и решить проблему. Переводя проблему из реального мира в область математики и придавая ей математическую структуру, они рассуждают и определяют смысл ограничений и допущений, присущих этой проблеме.
Применять математику ( employing mathematics ) способность применять математические понятия, факты, процедуры, рассуждения и инструменты для решения математически сформулированной проблемы и получения математических выводов Эта деятельность включает выполнение математических процедур, необходимых для получения результатов и математического решения (например, проводить арифметические вычисления, геометрические построения, переводить единицы измерения, решать уравнения, делать логические заключения с учетом математических допущений, извлекать математическую информацию из таблиц и графиков, представлять и манипулировать геометрическими формами в пространстве, анализировать данные).
Интерпретировать/оценивать результаты ( interpret and evaluate ) способность размышлять над математическим решением, результатами или выводами, интерпретировать и оценивать их в контексте реальной проблемы Эта деятельность включает перевод математического решения в контекст реальной проблемы и оценку того, являются ли результаты математического решения или рассуждений разумными и имеют смысл в контексте этой проблемы. Процесс интерпретации, применения и оценивания математических результатов охватывает и интерпретацию, и оценку полученного математического решения. При этом может потребоваться дать объяснения или аргументы в контексте проблемы, отражающие как процесс решения, так и его результаты.
Рассуждать Логика: Делать несложный вывод. Выбирать, давать соответствующее обоснование. Размышлять над аргументами, рассуждениями и выводами математического результата Рассуждать «над формулированием»: Представлять ситуацию различными способами, в том числе в соответствии с различными математическими теориями, делать соответствующие допущения. Объяснять и защищать созданные представления. Анализировать схожее и различия между моделью и мат. задачей, которую она моделирует. Определять, критиковать ограничения модели. Объяснять отношения между контекстно-обусловленным языком проблемы и формально-символическим языком ее представления на языке математики Рассуждать «над решением»: Понимать и использовать определения, правила, алгоритмы и формальные системы. Объяснять, как алгоритм работает, обнаруживать и исправлять ошибки в алгоритмах и процедурах. Обосновывать выбираемые и предложенные процедуры и модели с точки зрения получения результата. Размышлять над мат. решением и создавать объяснения и аргументацию, которые его поддерживают или опровергают Рассуждать «над результатом»: Аргументировать результат математически. Объяснить его разумность в рамках ситуации. Интерпретировать мат. результат в контексте ситуации в целях объяснения полученного результата
Области содержания математической грамотности Изменения и зависимости (алгебра) - 25% Пространство и форма (геометрия) - 25% Неопределенность и данные (статистика) - 25% Количество (арифметика) - 25%
Новые темы PISA-2021 Явления роста: линейные, нелинейные, квадратичные и экспоненциальные зависимости (Область: Изменение и зависимости) Геометрическая аппроксимация свойств нестандартных или незнакомых форм и объектов путем разбиения этих фигур и объектов на знакомые формы и объекты (Область: Пространство и форма) Компьютерное моделирование: анализ изменений, влияния переменных на результат; калькулятор (Область: Количество) Принятие решений в ситуациях неопределенности: использование вероятности и основных принципов комбинаторики для интерпретации ситуаций и прогнозирования (Область: Неопределенность и данные)
Контексты Личная жизнь – Мир человека (повседневные дела: покупки, приготовление пищи, игры, здоровье и др.) Образование/профессиональная деятельность – Мир профессий (школьная жизнь и трудовая деятельность, включают такие действия, как измерения, подсчеты стоимости, заказ материалов, например, для построения книжных полок в кабинете математики, оплата счетов и др.) Общественная жизнь – Мир социума (обмен валюты, денежные вклады в банке, прогноз итогов выборов, демография) Научная деятельность – Мир науки ( рассмотрение теоретических вопросов, например, анализ половозрастных пирамид населения, или решение чисто математических задач, например, применение неравенства треугольника).
