Теоретическая механика Практическая работа № 1 (2 семестр) Сегодня: четверг, 23 января 2025 г.
Тема : Равновесие твердого тела при действии пространственной системы сил Этапы выполнения работы: Сегодня: четверг, 23 января 2025 г. 1. Выделить твердое тело, равновесие которого следует рассмотреть для отыскания искомых величин; изобразить активные силы 2. Приложить к твердому телу соответствующие силы реакций связей; рассмотреть равновесие данного несвободного твердого тела как свободного тела, находящегося под действием активных сил и реакций связей; выбрать декартовую систему координат; 3. Записать уравнения равновесия для пространственной системы сил в проекциях на выбранные оси
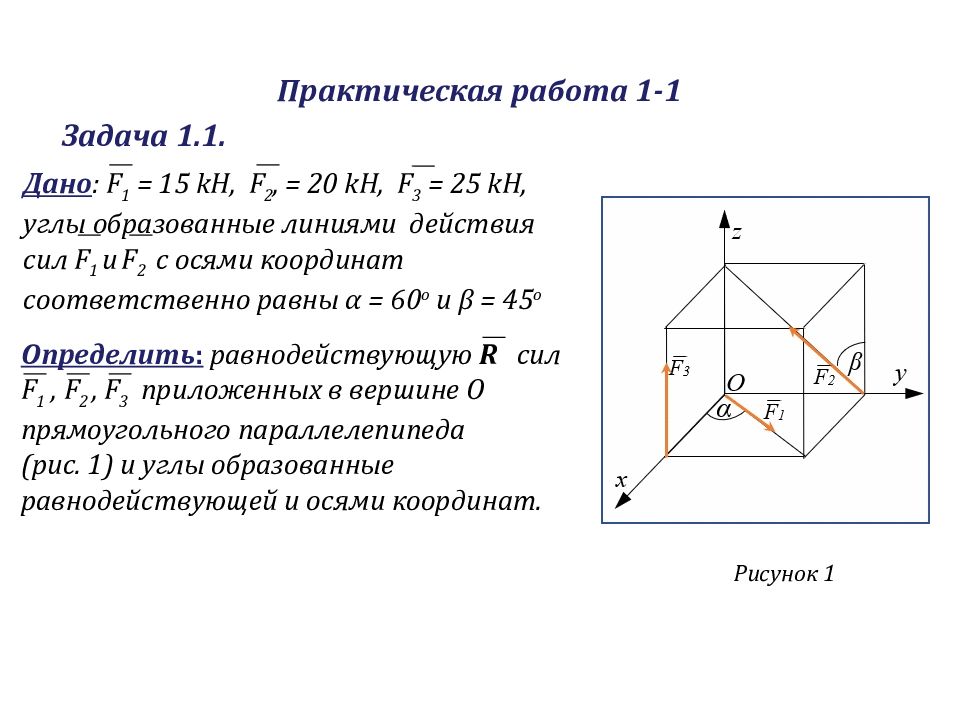
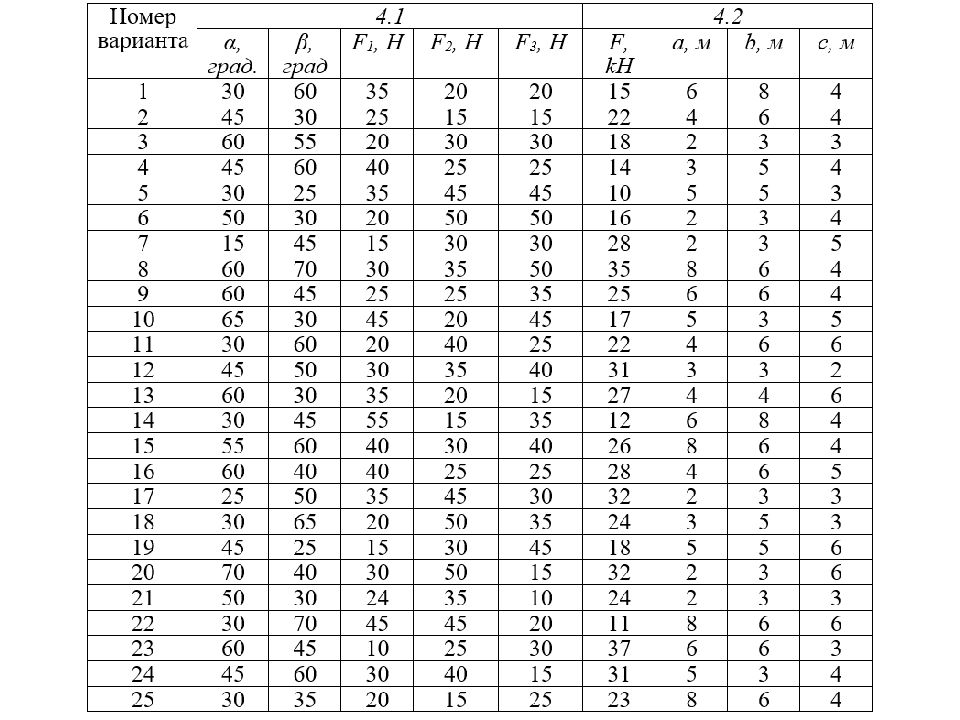
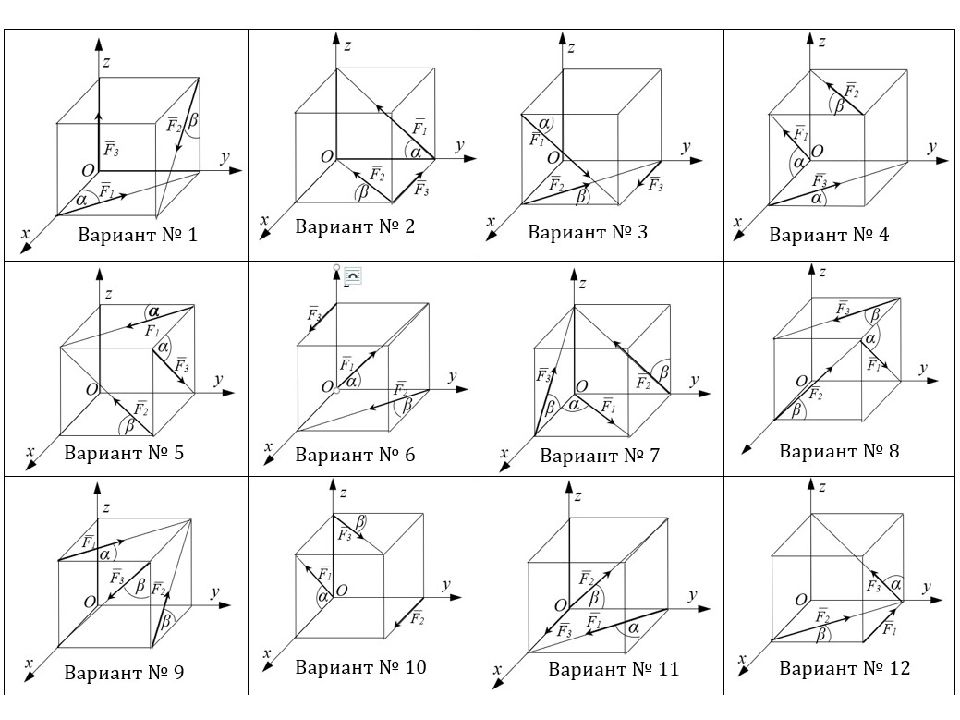
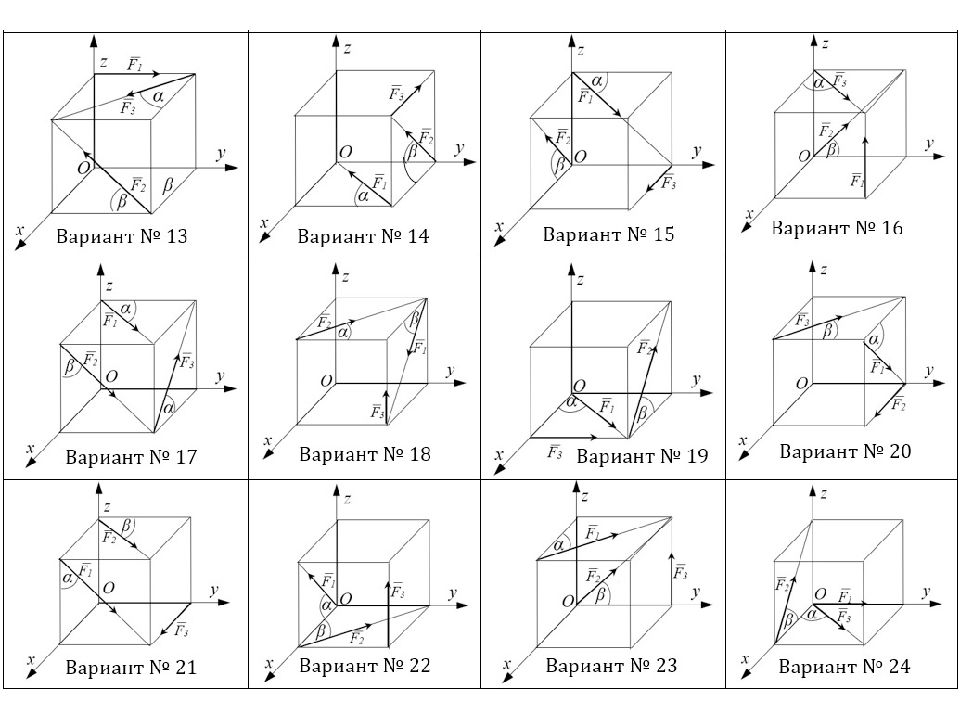
Рисунок 1 Определить : равнодействующую R сил F 1, F 2, F 3 приложенных в вершине О прямоугольного параллелепипеда (рис. 1) и углы образованные равнодействующей и осями координат. Дано : F 1 = 15 k Н, F 2, = 20 k Н, F 3 = 25 k Н, углы образованные линиями действия сил F 1 и F 2 с осями координат соответственно равны α = 60 о и β = 45 о Задача 1.1.
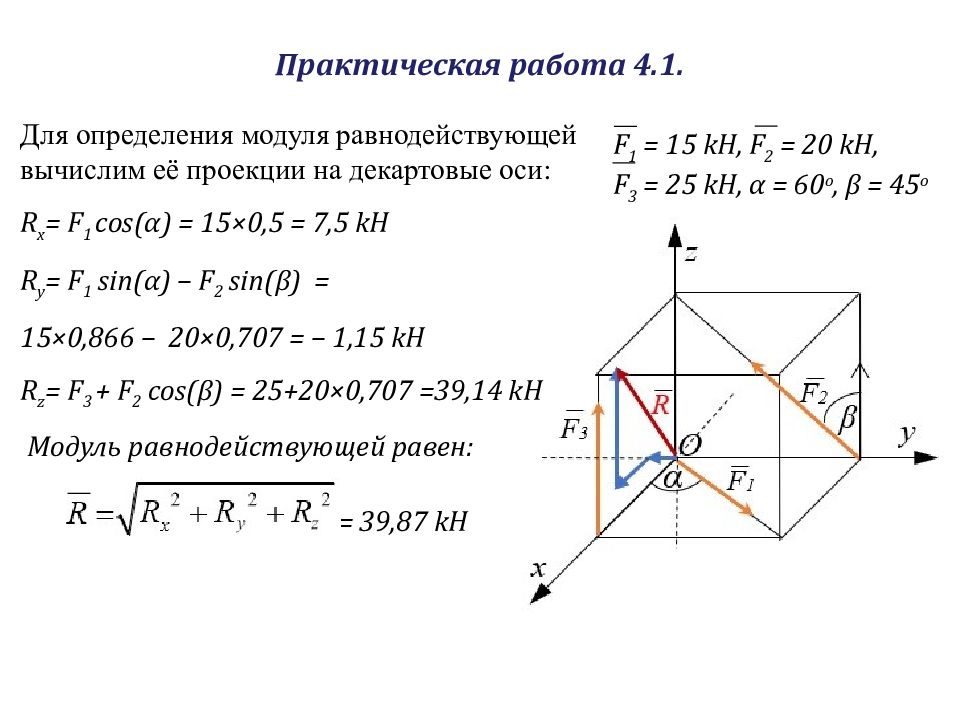
F 1 = 15 k Н, F 2 = 20 k Н, F 3 = 25 k Н, α = 60 о, β = 45 о = 39,87 kH Для определения модуля равнодействующей вычислим её проекции на декартовые оси: R x = F 1 cos(α) = 15×0,5 = 7,5 kH R y = F 1 sin(α) – F 2 sin ( β ) = 15×0,866 – 20×0,707 = – 1,15 kH R z = F 3 + F 2 cos ( β ) = 25+20×0,707 =39, 14 kH М одуль равнодействующей равен:
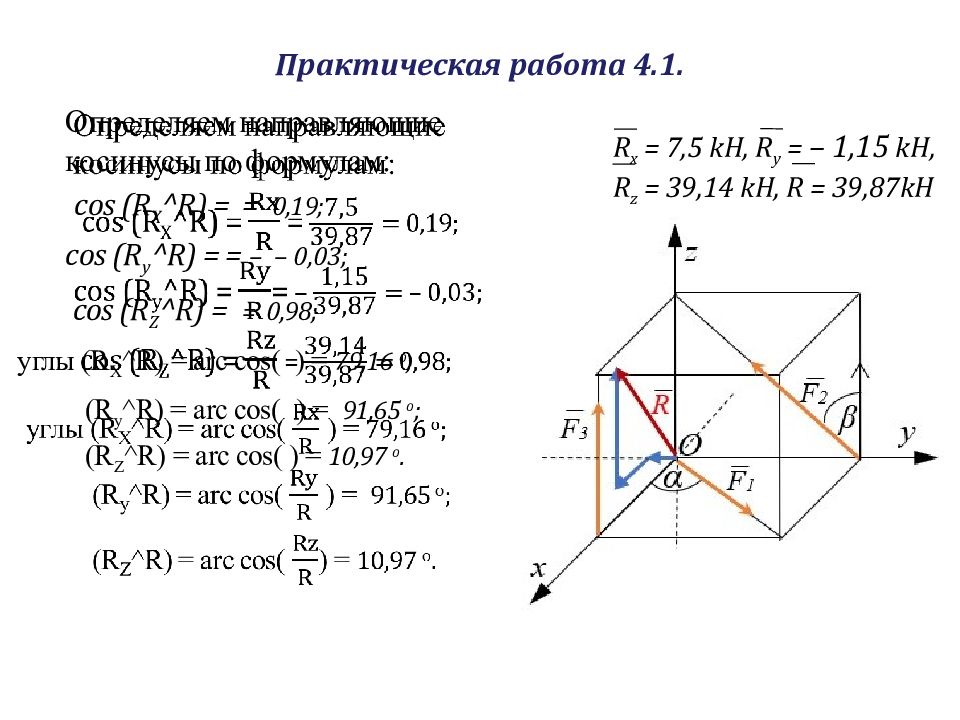
R x = 7,5 k Н, R y = – 1,15 k Н, R z = 39,14 k Н, R = 39,87k Н Определяем направляющие косинусы по формулам: cos (R X ^R) = = 0,19 ; cos ( R y ^R ) = = – – 0,03 ; cos (R Z ^R) = = 0,98 ; углы (R X ^R) = arc cos( ) = 79,16 о ; ( R y ^R ) = arc cos( ) = 91,65 о ; (R Z ^R) = arc cos( ) = 10,97 о.
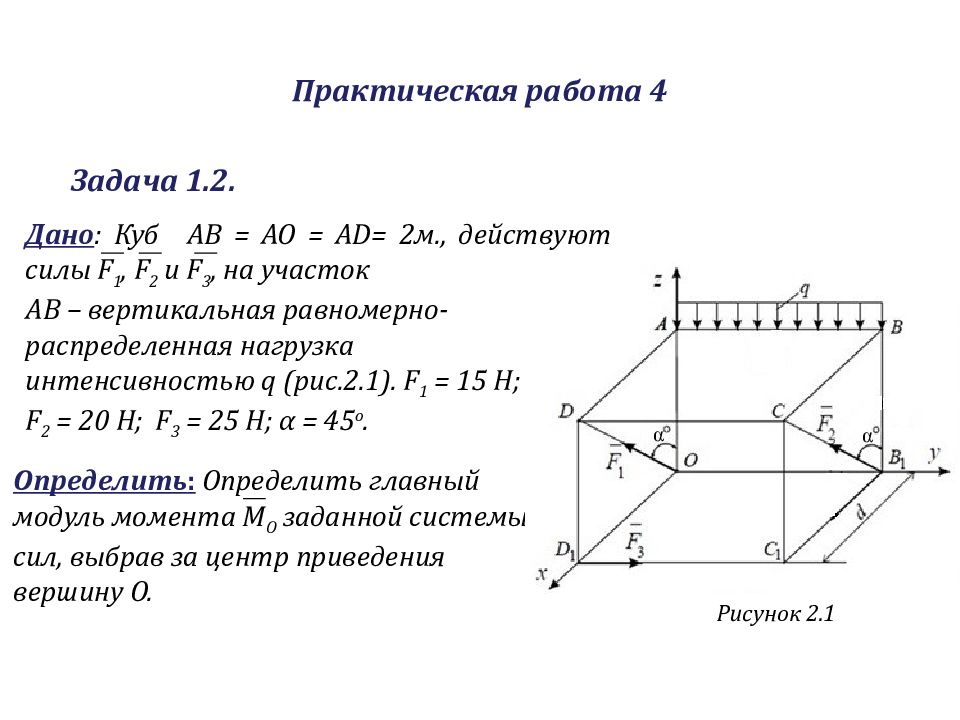
Рисунок 2.1 Определить : Определить главный модуль момента M O заданной системы сил, выбрав за центр приведения вершину O. Дано : К уб АВ = АО = AD= 2м., действуют силы F 1, F 2 и F 3, на участок AB – вертикальная равномерно-распределенная нагрузка интенсивностью q (рис.2.1). F 1 = 15 Н; F 2 = 20 Н; F 3 = 25 Н; α = 45 о. Задача 1.2. α α
Рисунок 2.2 Решение: Заменим распределенную нагрузку q равнодействующей Q приложенной в середине отрезка AB (рис 2.2). Найдём составляющие силы F 2 Q = q · AB = 6 kH F' 2 = F 2 ·sin α = 4,24 kH F " 2 = F 2 · cos α = 4,24 kH Найдём все проекции главного Момента M O системы сил относительно центра O, вычислим проекции на декартовы оси
Рисунок 2.2 т.к., поскольку силы и пересекают ось Ox, а составляющая параллельна этой оси. т.к., и Q пересекают ось Oy, а сила параллельна этой оси. т.к., поскольку сила ось O Z пересекает, а силы и Q параллельны этой оси. Тогда модуль главного момента вычисляем: Ответ : M O = 3,5 кН·м
