Поговорим о том, как теория вероятности помогает в жизни, спасает мир, какие технологии и достижения основываются на этих, казалось бы, нематериальных и далеких от жизни формулах и сложнейших вычислениях.
Теория вероятности — область математики, изучающая случайные события, и, естественно, их вероятность. Зародилась такого рода математика вовсе не в скучных серых кабинетах, а… игральных залах. Первые подходы к оценке вероятности того или иного события были популярны еще в Средневековье среди игроков того времени. Однако тогда они имели лишь эмпирическое исследование (то есть оценка на практике, методом эксперимента). Нельзя причислить авторство теории вероятности определенному человеку, так как работали над ней множество знаменитых людей, каждый из которых вложил свою толику. Первыми из таких людей стали Паскаль и Ферма. Они изучали теорию вероятности на статистике игры в кости. Они открыли первейшие закономерности. Х. Гюйгенс проделал схожую работу на 20 лет раньше, но теоремы не были сформулированы точно. Важный вклад в теорию вероятностей внёс Якоб Бернулли, Лаплас, Пуасон и многие другие. Пьер Ферма
Пьер де Ферма́ (фр. Pierre de Fermat, 17 августа 1601 — 12 января 1665) — французский математик-самоучка, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист, с 1631 года — советник парламента в Тулузе. Блестящий полиглот. Наиболее известен формулировкой Великой теоремы Ферма, «самой знаменитой математической загадки всех времён ». Самым известным и нашумевшим утверждением Ферма является его Великая теорема. Она многие десятилетия терзала умы лучших математиков и, даже после официальной публикации 1995 года, различные варианты ее доказательства продолжают поступать на математические кафедры всех университетов мира. При этом сама формулировка теоремы удивительно проста, впрочем, как и все остальные записи Ферма: Если n – натуральное и n>2, то уравнение a n + b n = c n не имеет решений в целых числах a, b и c, отличных от нуля. Ферма был знаком с Паскалем, он вел с ученым активную научную переписку. В итоге они, независимо друг от друга, создали основы великой науки современности – теории вероятностей. Результаты их трудов напечатал Гюйгенс в книге «О расчетах в азартной игре».
Мы все используем теорию вероятности на основе произошедших событий в нашей жизни и в жизни других людей. Г лавным понятием теории вероятностей является вероятность. Это слово, синонимом которого является слово « шанс », достаточно часто применяется в повседневной жизни. Думаю, каждому знакомы фразы: «Завтра, вероятно, выпадет снег», или «Вероятнее всего в выходные я поеду на природу», или «Это просто невероятно», или «Есть шанс получить зачет автоматом». Такого рода фразы на интуитивном уровне оценивают вероятность того, что произойдет некоторое случайное событие. В свою очередь математическая вероятность дает некоторую числовую оценку вероятности того, что произойдет некоторое случайное событие.
Практически вся современная экономика базируется на теории вероятностей. Выпуская на рынок определенный товар, грамотный предприниматель наверняка учтет риски, а также вероятности покупки на том или рынке, стране и т.д. Практически не представляют свою жизнь без теории вероятности брокеры на мировых рынках. Предсказывание денежного курса ( в котором точно не обойтись без теории вероятности) на денежных опционах или знаменитейшем рынке Forex дает возможность зарабатывать на данной теории серьезные деньги.
Вопрос : кто изображён на 100-долларовой купюре?
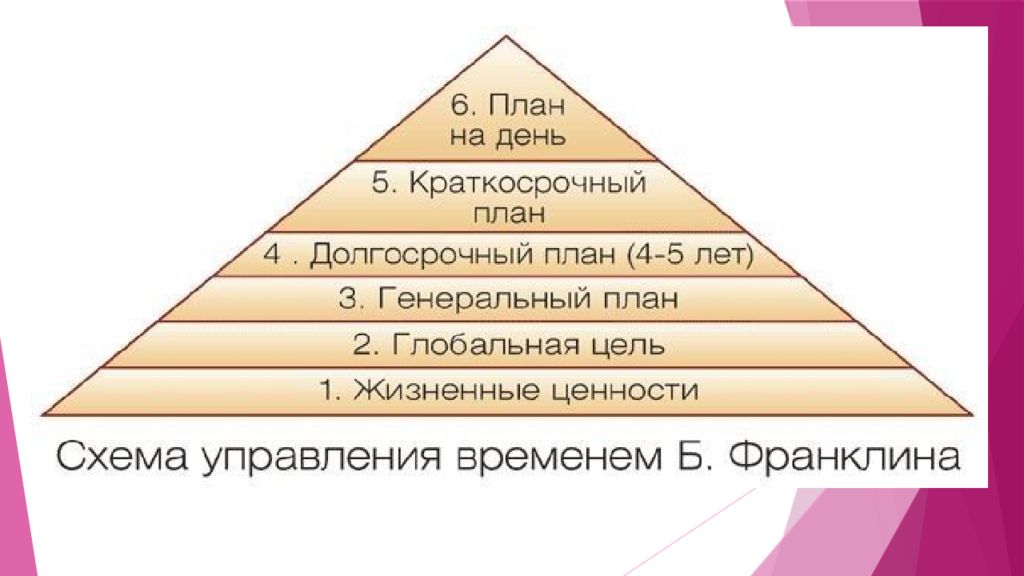
Бенджамин Франклин (1706-1790) – известный во всем мире американский политический деятель, дипломат, бизнесмен, ученый и изобретатель, иностранный член Российской академии наук. Будучи политиком, этот человек внес большой вклад в развитие Соединенных Штатов Америки, несмотря на то, что президентом страны он никогда не был. Биография Бенджамина Франклина весьма интересна. Он родился в простой семье и был пятнадцатым по счету ребенком. Учился Бенджамин в обычной сельской школе, закончил всего два класса, а уже в возрасте десяти лет был вынужден пойти работать. Будучи очень трудолюбивым и любознательным, он обожал учиться, получать новые знания. Он самостоятельно выучил несколько языков, серьезно интересовался наукой и даже придумал несколько изобретений. Главными качествами Бенджамина Франклина были высокая работоспособность, целеустремленность, умение грамотно распоряжаться своим временем, выделяя главные цели и отбрасывая ненужные. Благодаря этим качествам он смог добиться успеха в политике и многих других сферах. Франклин считал, что человек, который не ценит свое время, никогда не сможет добиться успеха в жизни. Именно ему принадлежит известная фраза «Время – деньги». Для того чтобы использовать время как можно рациональнее, Франклин разработал собственную систему планирования и достижения целей и пользовался ею всю жизнь. На сегодняшний день эта система планирования, называемая пирамидой Франклина, пользуется успехом у деловых людей и тех, кто желает прожить жизнь с пользой, не тратя времени впустую.
Теория вероятности присутствует, практически в любой сфере жизнедеятельности, причём она даёт возможность регулирования этих сфер: Благодаря оценке шансов той или иной неполадки (например, в космическом корабле ), мы знаем, какие усилия нам нужно приложить, что именно проверить, что вообще ожидать в тысячи километров от Земли. Возможности теракта в метрополитене, экономического кризиса или ядерной войны — все это можно выразить в процентах. А главное, предпринимать соответствующие контрдействия исходя из полученных данных.
Любую деятельность в любой сфере можно проанализировать, использую статистику, рассчитать вероятность появления тех или иных событий, и, благодаря теории вероятности, заметно улучшить
Т еория вероятностей порой подкидывает удивительные факты, в которые сложно поверить с первого взгляда — и которые, тем не менее, подтверждены наукой.
Этот парадокс был предложен Мартином Гарднером (учёный-математик)и формулируется так: « У мистера Смита двое детей. Хотя бы один ребенок — мальчик. Какова вероятность того, что и второй — тоже мальчик?»
Рассмотрим все возможные комбинации в семьях с двумя детьми: — Девочка/Девочка — Девочка/Мальчик — Мальчик/Девочка — Мальчик/Мальчик Вариант девочка/девочка нам не подходит по условиям задачи. Поэтому для семьи мистера Смита возможны три равновероятных варианта — а значит, вероятность того, что другой ребенок тоже окажется мальчиком, составляет ⅓. Именно такой ответ и давал сам Гарднер первоначально.
Представим, что мы встречаем мистера Смита на улице, когда он гуляет с сыном. Какова вероятность того, что второй ребенок — тоже мальчик? Поскольку пол второго ребенка никак не зависит от пола первого, очевидным (и правильным) ответом является ½.
Все зависит от того, как мы подходим к вопросу подсчета вероятности. В первом случае мы рассматривали все возможные варианты семьи Смита. Во втором — мы рассматривали все семьи, подпадающие под обязательное условие «должен быть один мальчик». Расчет вероятности пола второго ребенка велся с этим условием (в теории вероятностей это называется «условная вероятность» ), что и привело к результату, отличному от первого.
Классическая формулировка звучит так: «Допустим, некоему игроку предложили поучаствовать в игре, и ему необходимо выбрать одну из трех дверей. За двумя дверьми находятся котята, за одной — главный приз, автомобиль, ведущий знает расположение призов. После того, как игрок делает свой выбор, ведущий открывает одну из оставшихся дверей, за которой находится котёнок, и предлагает игроку изменить свое решение. Стоит ли игроку согласиться или лучше сохранить свой первоначальный выбор?» Вот типичный ход рассуждений : после того, как ведущий открыл одну из дверей и показал козу, игроку остается выбрать между двумя дверями. Машина находится за одной из них, значит, вероятность ее угадать составляет ½. Так что нет разницы — менять свой выбор или нет. И тем не менее, теория вероятностей гласит, что можно увеличить свои шансы на выигрыш, изменив решение. Разберемся, почему это так. Для этого вернемся на шаг назад. В тот момент, когда мы сделали свой изначальный выбор, мы разделили двери на две части: выбранная нами и две остальные. Очевидно, что вероятность того, что автомобиль прячется за «нашей» дверью, составляет ⅓ — соответственно, автомобиль находится за одной из двух оставшихся дверей с вероятностью ⅔. Когда ведущий показывает, что за одной из этих дверей — котёнок, получается, что эти ⅔ шанса приходятся на вторую дверь. А это сводит выбор игрока к двум дверям, за одной из которых (изначально выбранной ) автомобиль находится с вероятностью ⅓, а за другой — с вероятностью ⅔. Выбор становится очевидным. Что, разумеется, не отменяет того факта, что с самого начала игрок мог выбрать дверь с автомобилем.
События бывают более и менее вероятными. Предлагаю отправиться в путешествие к таким, вероятность которых невероятно близка к нулю.
Вероятность того, что при игре в «орлянку» монетка встанет на ребро, не так мала, как может показаться. Например, если вы совершите миллион бросков, то это случится около 150 раз, то есть в среднем 1 раз в 2 дня если вы будете кидать целый год по 8 часов в день.
Если же вы захотите дождаться того, чтобы монета встала на ребро два раза подряд, то придется кидать монеты в том же темпе около 35 лет.
Шанс угадать 6 номеров лотереи из 45 равен «1 к 8 145 060». Теперь понимаете, почему лотереи столь выгодны?
Для того, чтобы событие с вероятностью «один из миллиона» произошло хотя бы раз в жизни, нужно «пробовать» по 50 раз ежедневно. Например, если мы каждый день пересекаемся с 50 случайными людьми, то когда-нибудь в течение жизни столкнемся с тем, шанс встречи с которым «один на миллион».
Вероятность глобальной катастрофы для цивилизации в результате падения крупного астероида — «1 к 10 миллионам» (впрочем, для одного конкретного человека шанс погибнуть от астероида равен «1 к 500 тысячам», так что будем осторожны )).
Вероятность с первой попытки найти иголку в стоге сена — примерно «1 к 100 миллионам».
А можно ли случайно собрать разобранный кубик Рубика 3×3×3? Любая конкретная расстановка имеет шанс оказаться правильной всего лишь «1 к 4.32*10 19 », так что на сборку может потребоваться 26 лет.
Человек, вообще не умеющий играть в шахматы, имеет шанс выиграть у гроссмейстера примерно «1 к 10 100 ».
Математика – не скучная наука. Мы бы рады ею не интересоваться, но она – везде! Мы живём в теории вероятности. Поэтому очень полезно знать её основы. Если даже вероятность найти иголку в стоге сена существует, то уж вероятность достичь грандиозных жизненных целей – тем более!!! Только необходимо упорство в их достижении и трудолюбие – и тогда вероятность положительного исхода будет стремиться к 1!
