Слайд 2: Определения
Приближенное значение случайной величины, вычисленное по ограниченному числу опытов, т. е. выборке, содержит элемент случайности и называется оценкой. Статистические оценки делятся на точечные и интервальные. Оценка определяемая одним числом, называется точечной.
Слайд 3: Требования к оценке
Оценка для параметра представляет собой функцию величин 1) Несмещенность – среднее значение средних величин равно среднему значению выборки
Слайд 4: Требования к оценке
2 ) Состоятельность – с увеличением числа опытов случайная величина приближается (сходится по вероятности) к параметру
Слайд 5: Требования к оценке
3) Эффективность – оценка обладает наименьшей дисперсией по сравнению с другими
Слайд 6: Точечные оценки
Среднее выборочное наблюдаемых значений – это состоятельная и несмещенная оценка. Эффективность оценки зависит от вида распределения случайной величины. В ыборочная дисперсия, среднее квадратическое отклонение и исправленная выборочная дисперсия – несмещенные оценки.
Слайд 7
При обработке статистической информации широко используют распределение статистик, которые вычисляются по выборке из нормально распределенной генеральной совокупности. Квантилью порядка р распределения случайной величины X называется де й ствительное число, удовлетворяющее уравнению P(X<. (определяются по специальным стат.таблицам )
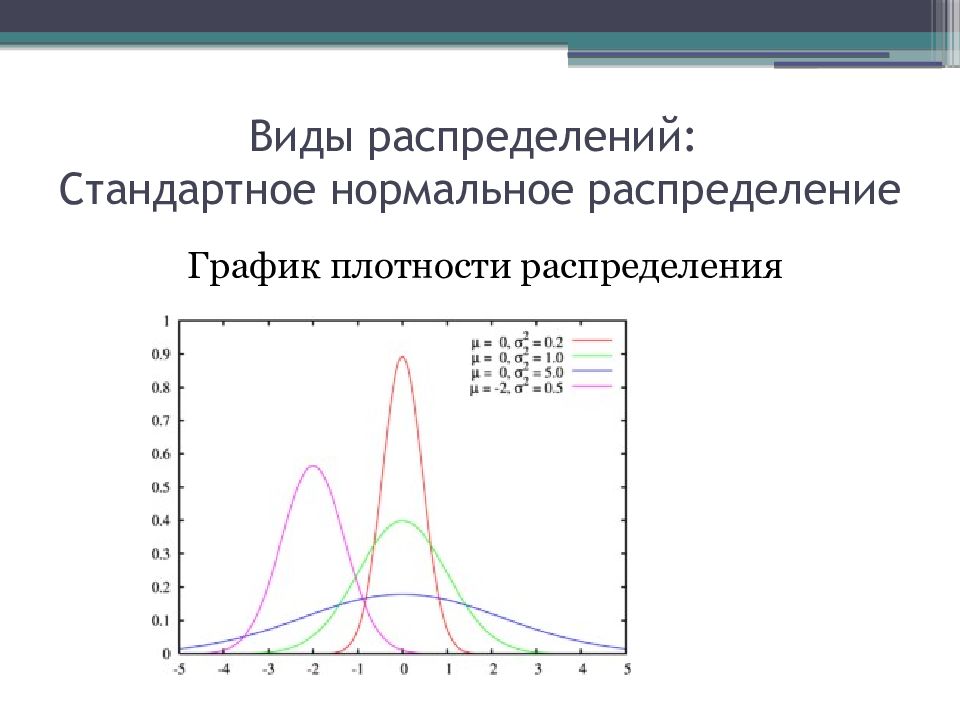
Слайд 8: Виды распределений: Стандартное нормальное распределение
График плотности распределения
Слайд 9: Виды распределений: t- распределение (Стьюдента)
Распределение Стьюдента с k степенями свободы, t- распределение симметрично. При увеличении объема выборки распределение стремится к нормальному.
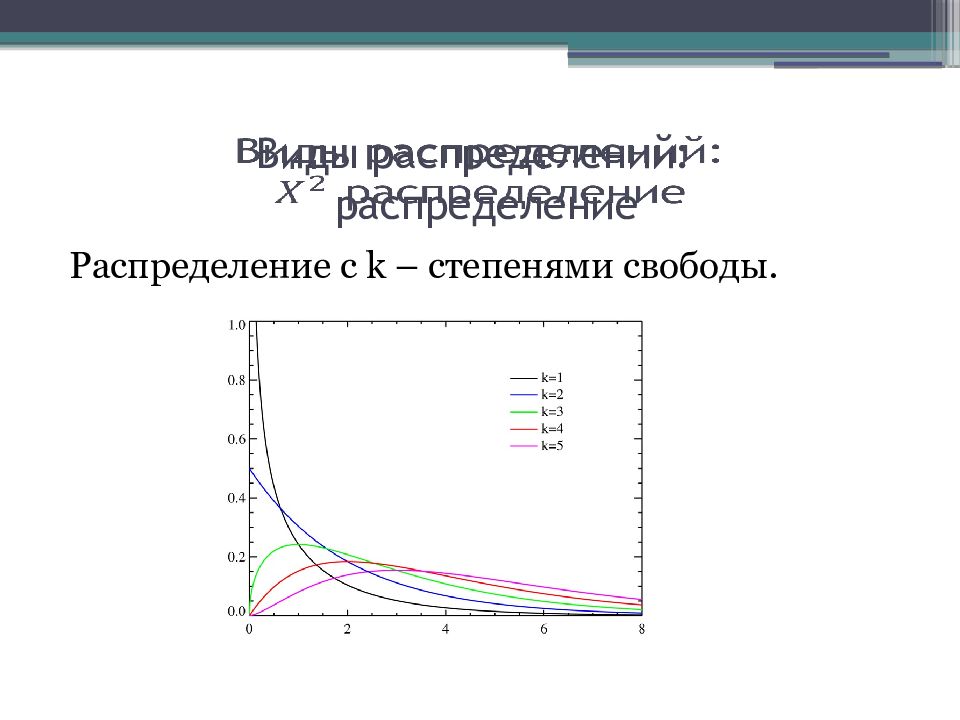
Слайд 10: Виды распределений: распределение
Распределение с k – степенями свободы.
Слайд 11: Интервальная оценка
Для оценки точности и надежности вычисленного параметра используют доверительные интервалы и доверительные вероятности. - точечная оценка параметра; - некоторая малая, положительная величина.
Слайд 12: Определение
Доверительный интервал - интервал к оторый с вероятностью накрывает истинное значение параметра. - достаточно большая вероятность, при которой событие можно считать практически достоверным. - вероятность допустить ошибки при вычислении параметра (очень малая величина, уровень значимости).
Слайд 13: Свойства интервальной оценки
1) Точность интервала определяется (чем меньше, тем точнее интервал). 2) Надежность интервала определяется доверительной вероятность (надежностью). Интервал может быть точным или надежным.