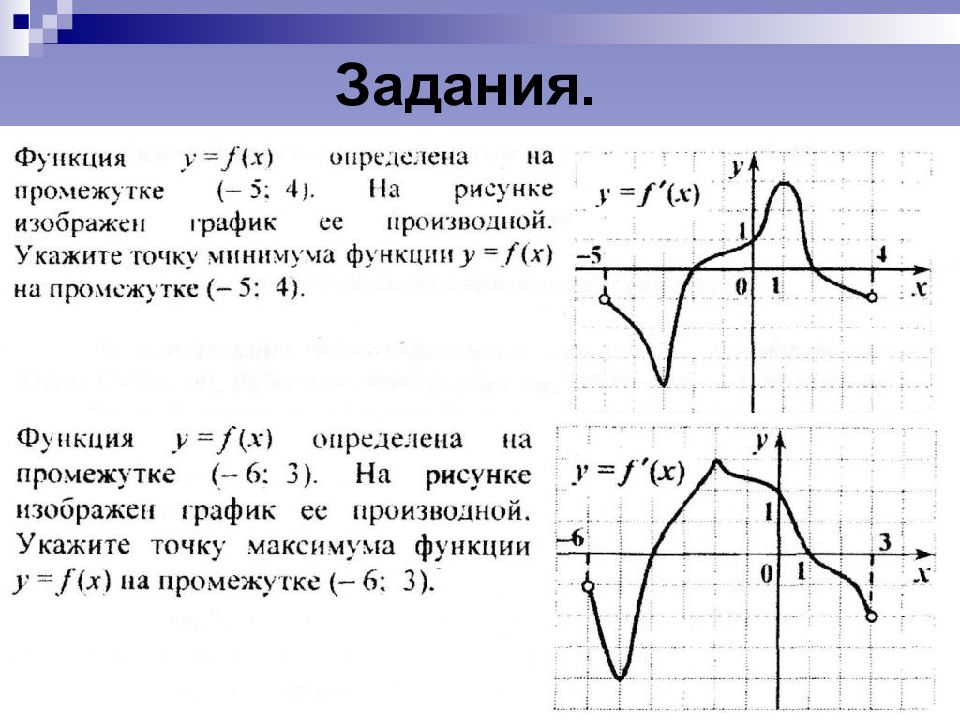
Слайд 2: Определение
Точку x = x 0 называют точкой минимума функции y = f (x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки x = x 0 ) выполняется равенство f (x) > f (x 0 ). Значение функции в точке минимума обычно обозначают y min.
Слайд 3: Определение
Точку x = x 0 называют точкой максимума функции y = f (x), если у этой точки существует окрестность, для всех точек которой, кроме самой точки x = x 0, выполняется равенство f (x) < f (x 0 ). Значение функции в точке максимума обычно обозначают y max.
Слайд 4
Точки минимума и максимума функции объединяют общим термином – точки экстремума.
Слайд 5: Достаточные условия экстремума
Пусть функция y = f (x) непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку x = x 0. Тогда: если у этой точки существует такая окрестность, в которой при x < x 0 выполняется неравенство f’ (x) < 0, а при x > x 0 – неравенство f’ (x) > 0, то x = x 0 – точка минимума функции y = f (x) ;
Слайд 6
если у этой точки существует такая окрестность, в которой при x < x 0 выполняется неравенство f’ (x) > 0, а при x > x 0 – неравенство f’ (x) < 0, то x = x 0 – точка максимума функции y = f (x) ; если у этой точки существует такая окрестность, что в ней и слева, и справа от точки x 0 знаки производной одинаковы, то в точке x 0 экстремума нет.