Слайд 2: План занятия
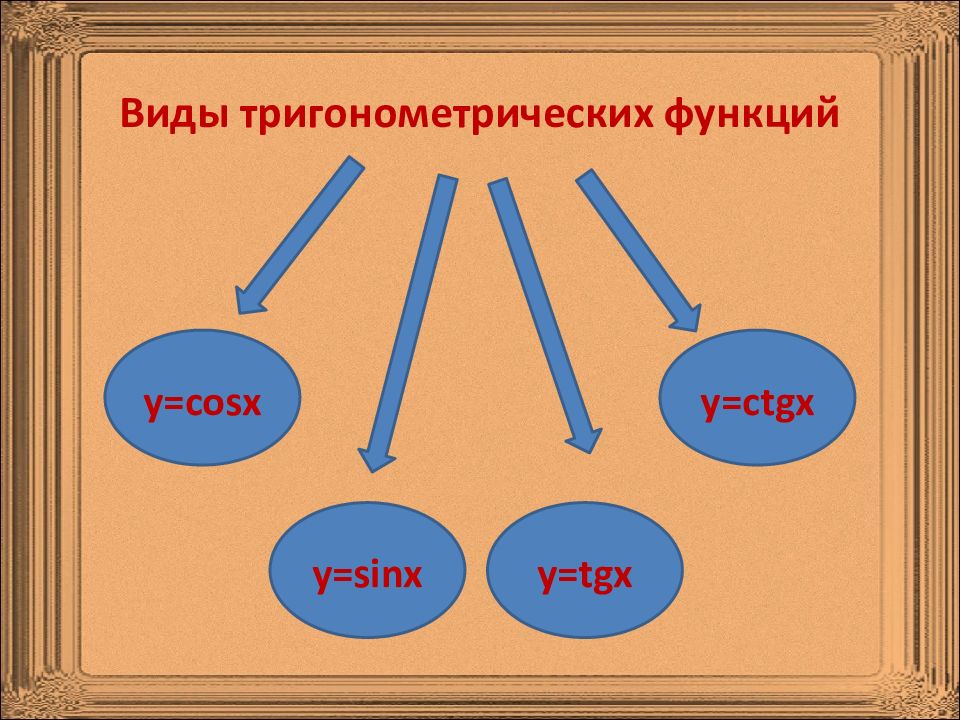
Виды тригонометрических функций Определения тригонометрических функций Графики тригонометрических функций Свойства тригонометрических функций
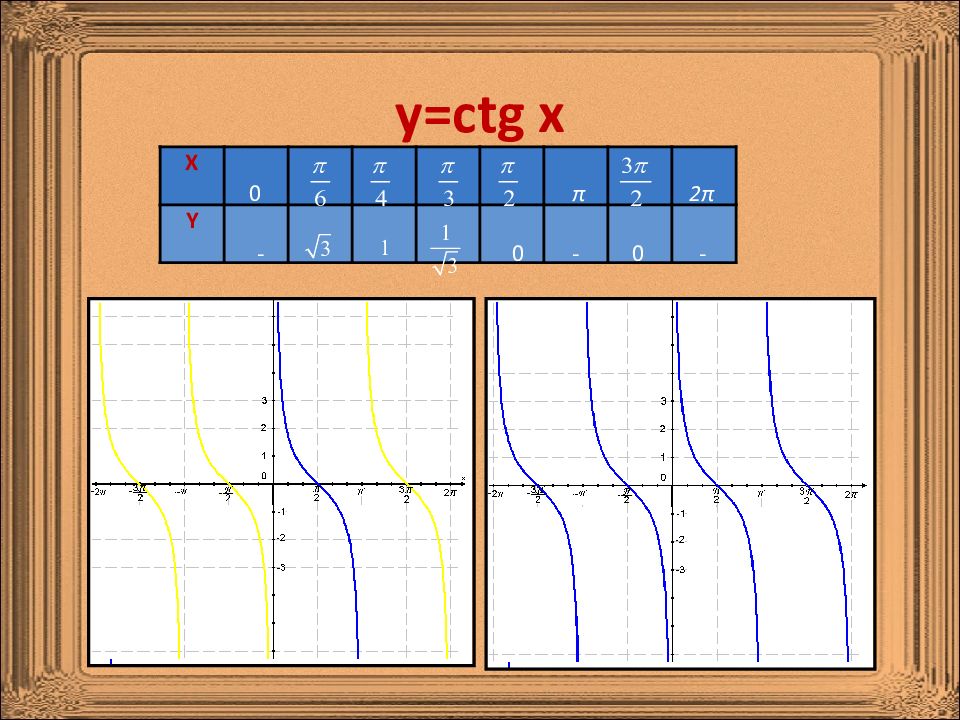
Слайд 4: Определения
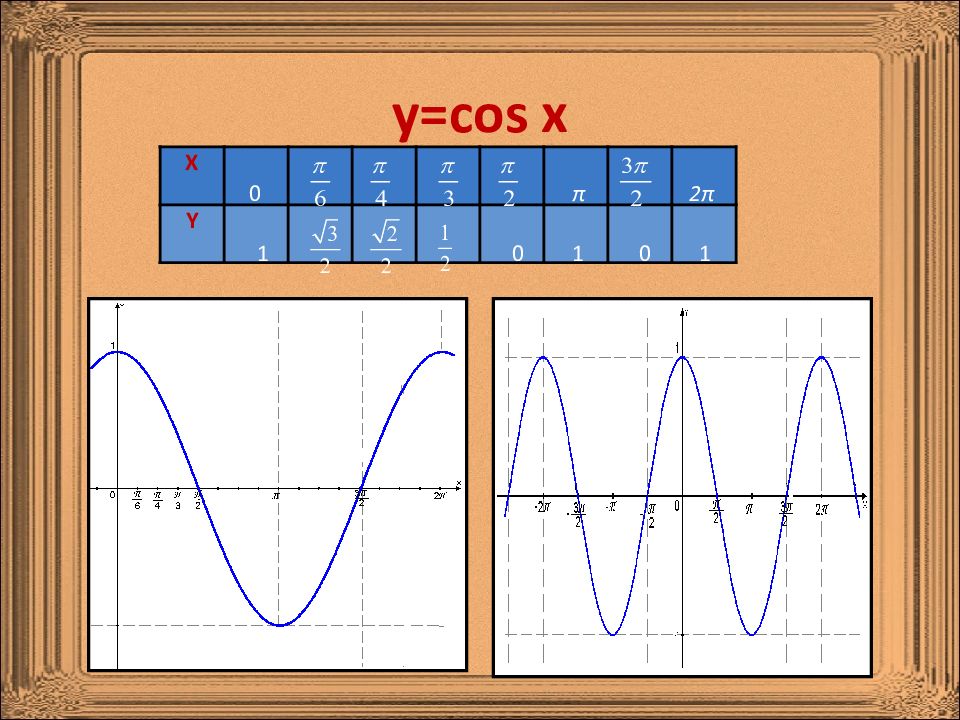
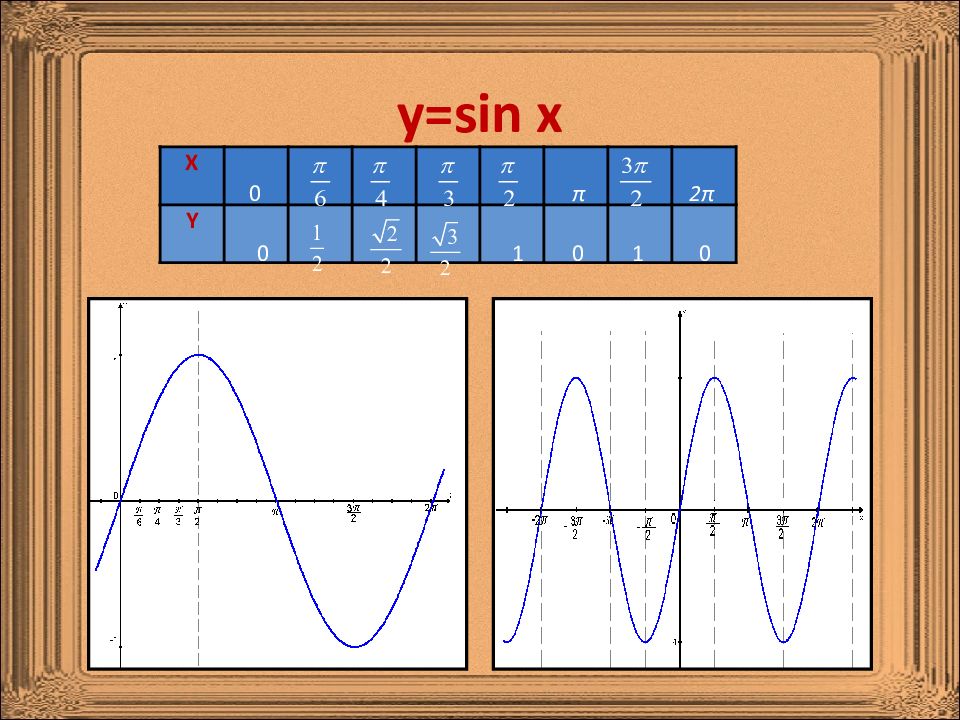
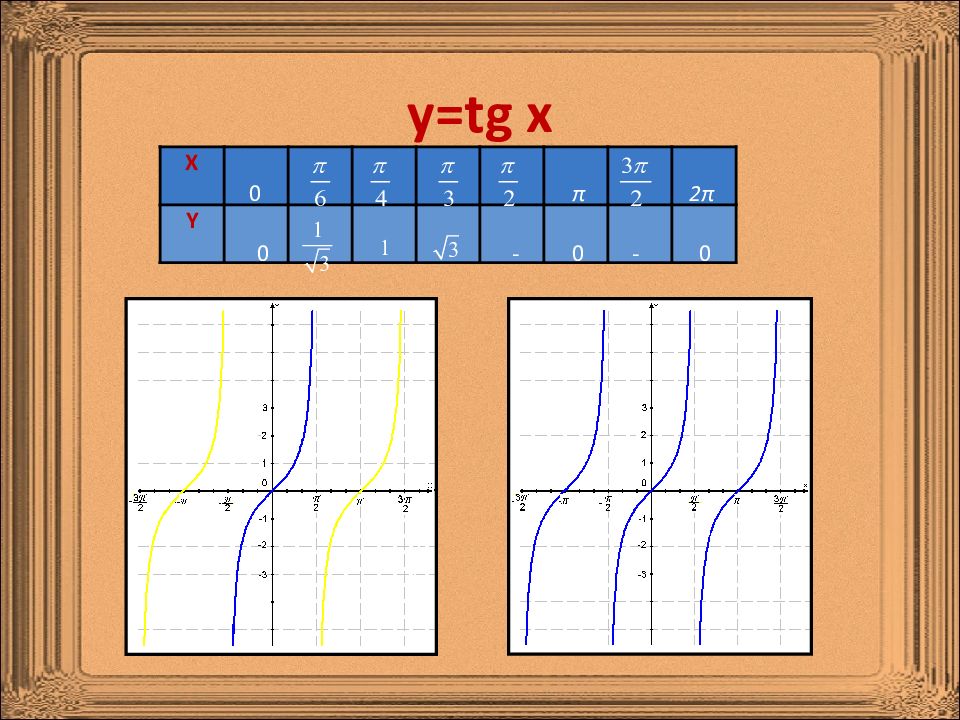
Определение 1. Числовые функции, заданные формулами y=cosx и y=sinx, называют соответственно косинусом и синусом. Определение 2. Числовые функции, заданные формулами y=tgx и y=ctgx, называют соответственно тангенсом и котангенсом. Определения
Слайд 11: Свойства тригонометрических функций
у= cos x у= sin x 1. Область определения функции D(y)= (-∞;+∞) D(y)= (-∞;+∞) 2. Область значения функции Е (y)= [-1;1] [-1;1] Е (y)=
Слайд 12: Свойства тригонометрических функций
у= cos x у= sin x 3. Четность функции Функция четная, т.к. график симметричен относительно оси Ох Функция нечетная, т.к. график симметричен относительно начала координат cos (-x)=cos x Значит, справедливо равенство: Значит, справедливо равенство: sin (-x)=-sin x
Слайд 13: Свойства тригонометрических функций
у= cos x у= sin x 4. Периодичность функции Функция периодическая, cos (x +2 π )=cos x основной период функции равен 2 π. Значит, справедливо равенство: sin (x +2 π )=sin x Значит, справедливо равенство: Функция периодическая, основной период функции равен 2 π.
Слайд 14: Свойства тригонометрических функций
у= cos x у= sin x 5. Нули функции Рассмотрим функцию на промежутке [0;2 π ]: x=0, при Oy : y= 1 x=0, при Oy : y=0 Рассмотрим функцию на промежутке [0;2 π ]: у = 0, при O х : O х : у = 0, при
Слайд 15: Свойства тригонометрических функций
у= cos x у= sin x 6. Промежутки монотонности Функция возрастает: Функция убывает: Функция возрастает: Функция убывает:
Слайд 16: Свойства тригонометрических функций
у= tg x у= ctg x 1. Область определения функции D(y)= D(y)= 2. Область значения функции Е (y)= [-∞;+∞] Е (y)= [-∞;+∞]
Слайд 17: Свойства тригонометрических функций
у= tg x у= ctg x 3. Четность функции Функция нечетная, т.к. график симметричен относительно начала координат tg (-x)=-tg x Значит, справедливо равенство: Значит, справедливо равенство: ctg (-x)=-ctg x Функция нечетная, т.к. график симметричен относительно начала координат
Слайд 18: Свойства тригонометрических функций
у= tg x у= ctg x 4. Периодичность функции Функция периодическая, tg (x + π )=tg x основной период функции равен π. Значит, справедливо равенство: ctg (x + π )=ctg x Значит, справедливо равенство: Функция периодическая, основной период функции равен π.
Слайд 19: Свойства тригонометрических функций
у= tg x у= ctg x 5. Нули функции Рассмотрим функцию на промежутке [ - π /2; π /2]: x=0, при Oy : y=0 нет Oy : Рассмотрим функцию на промежутке [ - π /2; π /2]: у = 0, при O х : O х : у = 0, при