Логарифмы Автор: Кузнецова Лариса Викторовна, преподаватель ГБОУ СПО РО « Ростовский-на-Дону автодорожный колледж» Приложение 2 к М Р открытого занятия по дисциплине МАТЕМАТИКА по теме: «ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ, ЕЁ ГРАФИК И СВОЙСТВА» ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СПО РО «РОСТОВСКИЙ-НА-ДОНУ АВТОДОРОЖНЫЙ КОЛЛЕДЖ»
Безграничны приложения показательной и логарифмической функций в самых различных областях науки и техники! Первые логарифмические таблицы были опубликованы в 1614 году, составленные Джоном Непером. Они помогли астрономам и инженерам, сокращая время на вычисления, и тем самым, как сказал знаменитый французский ученый Лаплас, «удлиняли жизнь вычислителям». Логари́фм - от греч. λόγος — «слово», «отношение» и ἀριθμός — «число», «показатель»
Параллельно с Непером над составлением таблицы логарифмов работал другой любитель математики - Йост Бюрги. Он был швейцарским часовщиком и мастером астрономических приборов. Бюрги составил таблицы логарифмов раньше, но только в 1620 году издал свою книгу "Таблицы арифметической и геометрической прогрессии с обстоятельным наставлением, как пользоваться ими при всякого рода вычислениях". Йост Бюрги (1552 - 1632)
В 1623 г., т. е. всего через 9 лет после издания первых таблиц, английским математиком Эдмундом Гантером была изобретена первая логарифмическая линейка, ставшая рабочим инструментом для многих поколений вплоть до появления ЭВМ.
Логарифми́ческая спира́ль или изогональная спираль — особый вид спирали, часто встречающийся в природе. Логарифмическая спираль была впервые описана Декартом и позже интенсивно исследована Бернулли, который называл её Spira mirabilis — «удивительная спираль». Декарт искал кривую, обладающую свойством, подобным свойству окружности, так чтобы касательная в каждой точке образовывала с радиус-вектором в каждой точке один и тот же угол. Он показал, что это условие равносильно тому, что полярные углы для точек кривой пропорциональны логарифмам радиус-векторов.
Рене Декарт (1596-1650гг.) Французский математик Первый ученый, открывший эту удивительную кривую. Логарифмическая спираль обладает замечательным свойством восстанавливать свою форму после различных преобразований.
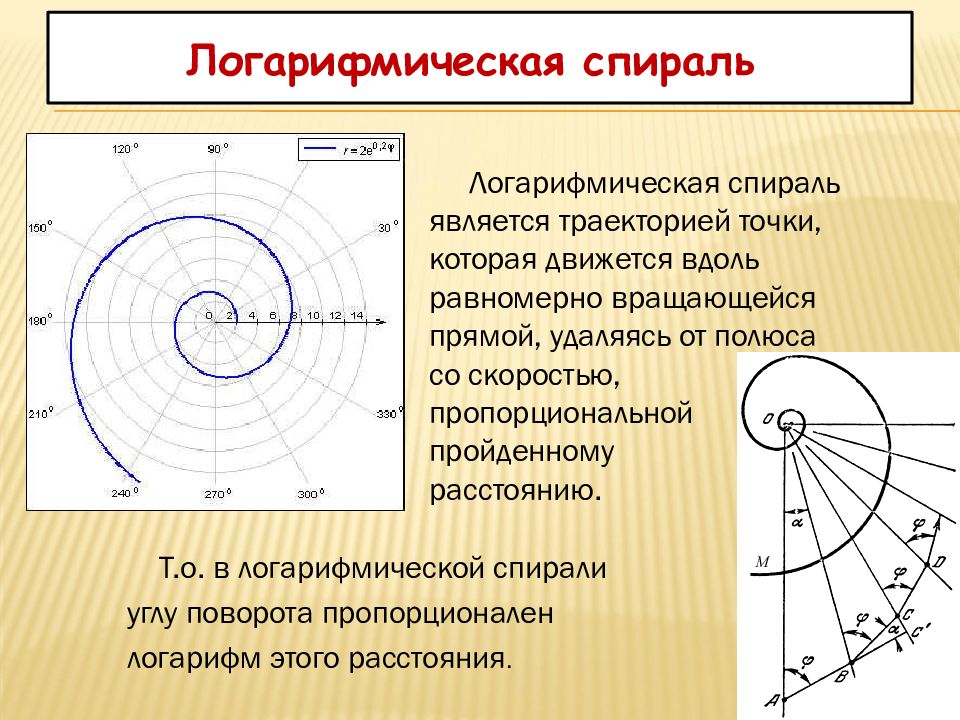
Логарифмическая спираль является траекторией точки, которая движется вдоль равномерно вращающейся прямой, удаляясь от полюса со скоростью, пропорциональной пройденному расстоянию. Т.о. в логарифмической спирали углу поворота пропорционален логарифм этого расстояния.
Самое интересное и удивительное в том, что логарифмическая спираль возникает в нашей жизни в связи с самыми разными природными формами. Размер витков логарифмической спирали постепенно увеличивается, но их форма остаётся неизменной. Возможно, в результате этого свойства логарифмическая спираль появляется в определённых растущих формах, подобных раковинам моллюсков и шляпкам подсолнечников. Логарифмическая спираль
По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника Иллюстрация модели Вогеля для n =1.500
По логарифмической спирали свёрнуты раковины многих улиток и моллюсков.
Живые существа обычно растут, сохраняя общее очертание своей формы. При этом они растут чаще всего во всех направлениях - взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении.
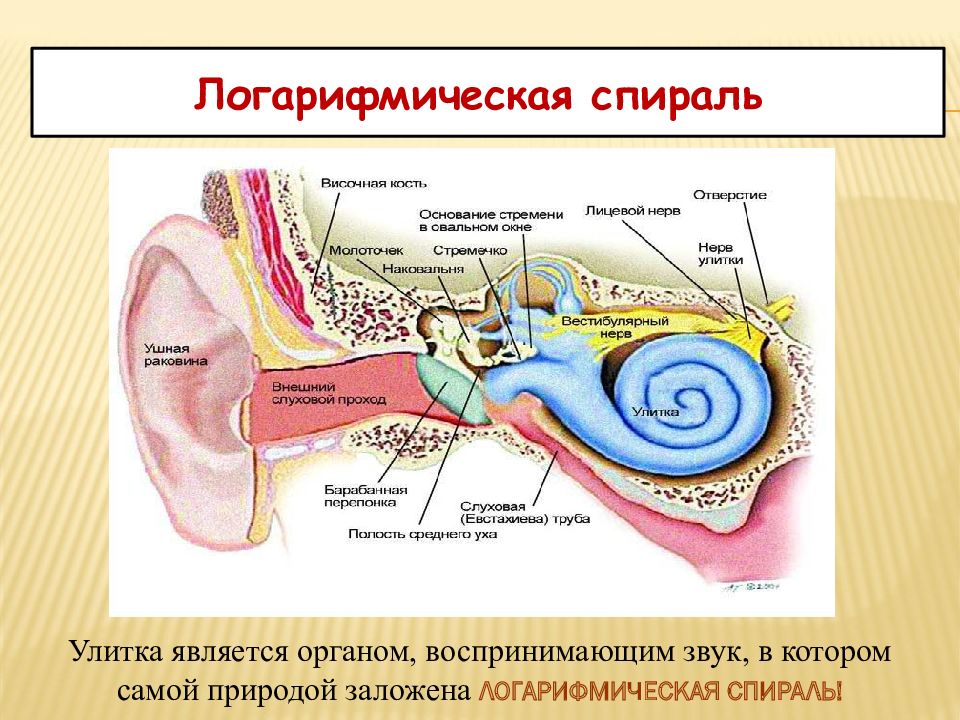
Улитка является органом, воспринимающим звук, в котором самой природой заложена ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ!
По логарифмическим спиралям закручены многие Галактики, в частности, Галактика, которой принадлежит Солнечная система. Распределение числа звезд на небе по яркости - логарифмическая зависимость.
И эту спираль мы повсюду встречаем: к примеру, ножи в механизме вращая. В изгибе трубы мы ее обнаружим – турбины тогда максимально послужат!
Молекула ДНК закручена двойной спиралью. Гете называл спираль "кривой жизни".
Мы постарались доказать, что математику не зря называют «Царицей наук», что ей больше, чем какой-либо другой науке, свойственны красота, гармония, изящность и точность. До новых встреч!
http://ru.wikipedia.org/wiki/Логарифм http://www.yoga-gazeta.ru http://festival.1september.ru/articles/506921/
