Алгебра логики — это раздел математической логики, изучающий высказывания со стороны их логических значений (истинности или ложности) и логических операций над ними. Объектами алгебры логики являются высказывания. Высказыванием в алгебре логики называется выражение, относительно которого можно сказать, истинно оно или ложно. Говорят, что высказывание принимает значение "истина" (еще обозначается 1) или "ложь" (обозначается 0). Для составления комбинации высказываний используются логические операции, результат которых может принимать бинарные значения 0 или 1, ложь или истина. У каждой операции есть свой приоритет как в обычной математике.
Для решение ЕГЭ достаточно будет следующих операций, растравленных по их приоритету выполнения: Отрицание Конъюнкция (логическое умножение ) Дизъюнкция (логическое сложение) Импликация (следование) Эквивалентность (равносильность) Логические операции и их приоритет
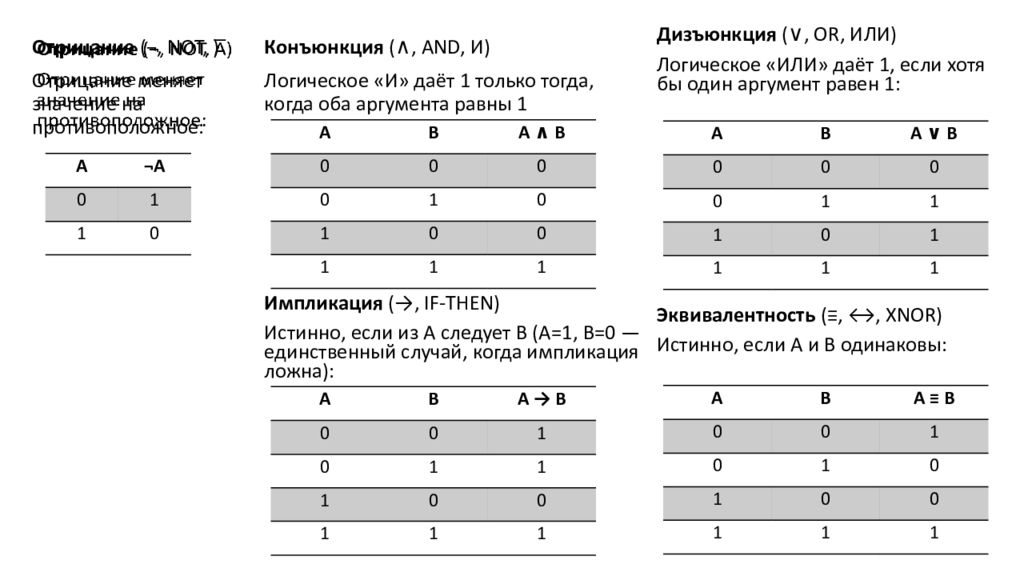
Конъюнкция (∧, AND, И) Логическое «И» даёт 1 только тогда, когда оба аргумента равны 1 А B A ∧ B 0 0 0 0 1 0 1 0 0 1 1 1 Дизъюнкция (∨, OR, ИЛИ) Логическое «ИЛИ» даёт 1, если хотя бы один аргумент равен 1: А B A ∨ B 0 0 0 0 1 1 1 0 1 1 1 1 Эквивалентность (≡, ↔, XNOR) Истинно, если A и B одинаковы: А B A ≡ B 0 0 1 0 1 0 1 0 0 1 1 1 Импликация (→, IF-THEN) Истинно, если из A следует B (A=1, B=0 — единственный случай, когда импликация ложна): А B A → B 0 0 1 0 1 1 1 0 0 1 1 1 Отрицание (¬, NOT, ) Отрицание меняет значение на противоположное: А ¬А 0 1 1 0
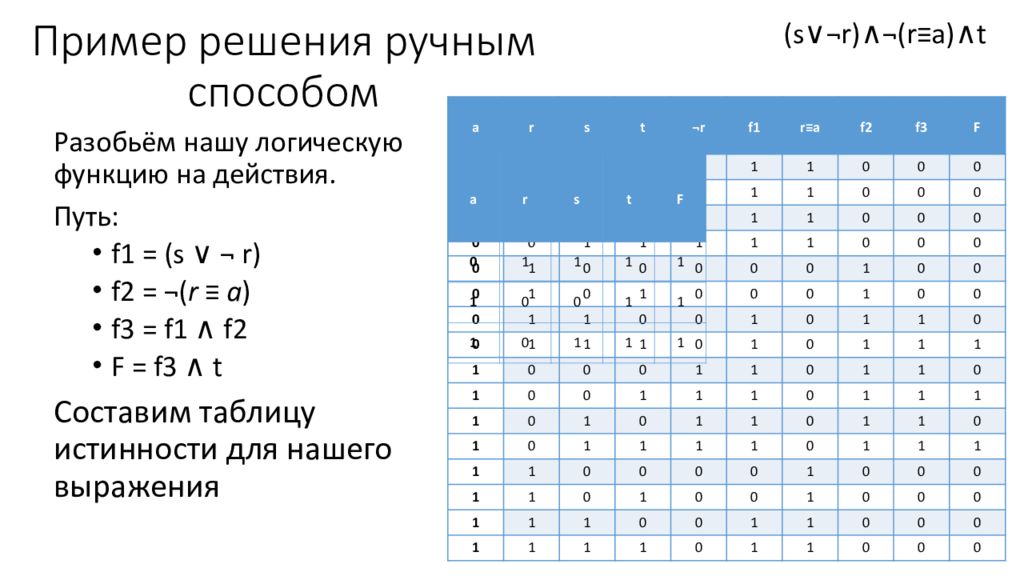
Разобьём нашу логическую функцию на действия. Путь : f 1 = (s ∨ ¬ r) f 2 = ¬( r ≡ a ) f3 = f1 ∧ f2 F = f3 ∧ t Составим таблицу истинности для нашего выражения Пример решения ручным способом (s∨¬r)∧¬(r≡a)∧t a r s t ¬r f1 r≡a f2 f3 F 0 0 0 0 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 1 0 0 0 1 1 0 0 1 0 1 1 0 0 1 1 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 1 0 1 0 0 1 1 1 0 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0 1 1 1 1 0 1 1 1 1 1 0 0 0 0 1 0 0 0 1 1 0 1 0 0 1 0 0 0 1 1 1 0 0 1 1 0 0 0 1 1 1 1 0 1 1 0 0 0 a r s t F 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1
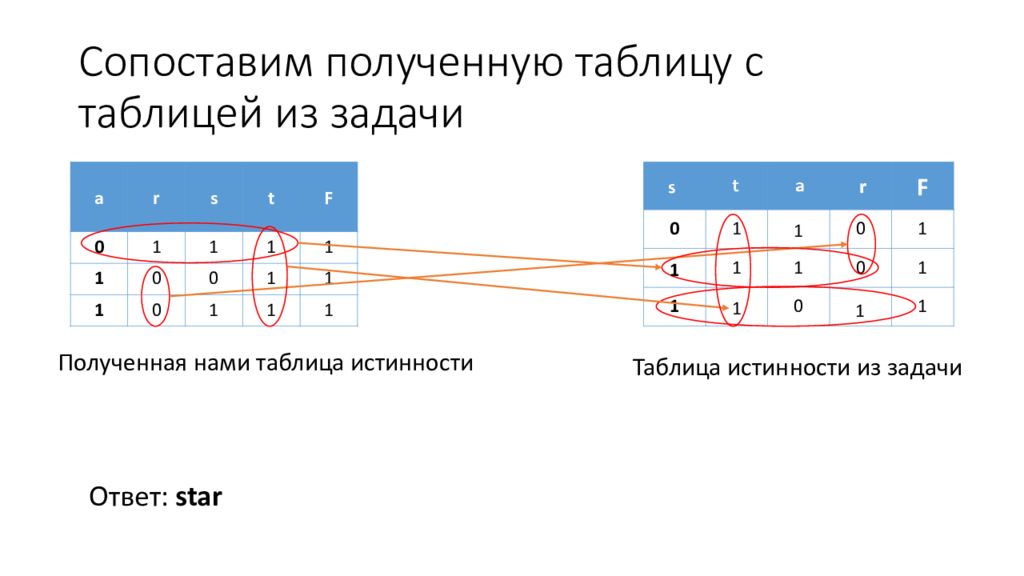
F 0 1 0 1 1 1 0 1 1 0 1 a r s t F 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 Полученная нами таблица истинности Таблица истинности из задачи 1 1 1 1 Ответ: star
Вложенными циклами будем перебирать переменные s, r, a, t. print ( ‘ a r s t’ ) for a in (0, 1): for r in (0, 1): for s in (0, 1): for t in (0, 1): Напишем логическое выражение на Python внутри циклов: F = (s or ( not r)) and ( not (r == a)) and t По условию задачи, нам необходимо, чтобы F было всегда истинным: if F == 1: (s∨¬r)∧¬(r≡a)∧t Осталось вывести внутри условия все переменные. Полный код: print ( ‘a r s t’ ) for a in (0, 1): for r in (0, 1): for s in (0, 1): for t in (0, 1): F = (s or ( not r)) and ( not (r == a)) and t if F == 1: print (s, r, a, t)
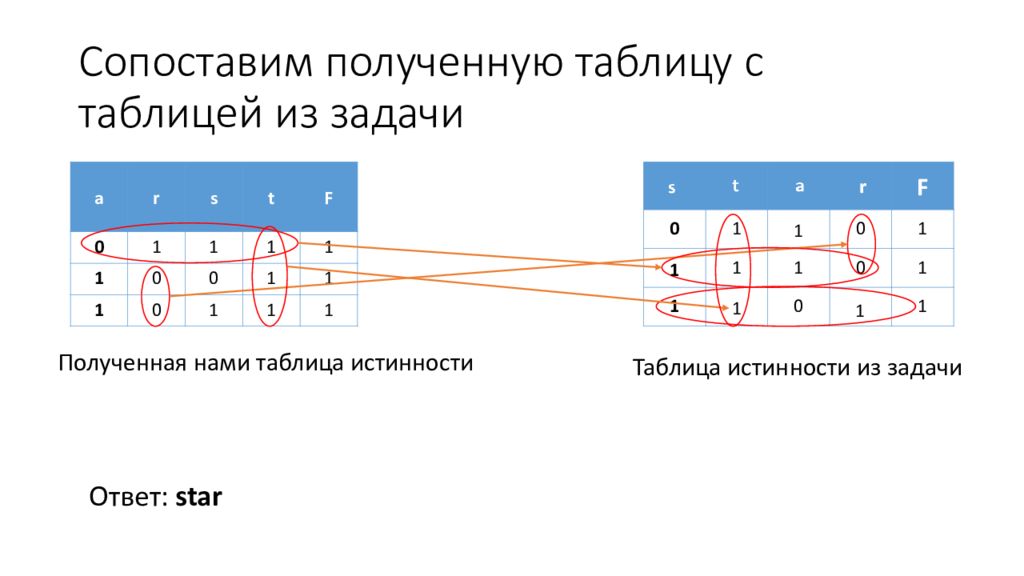
F 0 1 0 1 1 1 0 1 1 0 1 a r s t F 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 Полученная нами таблица истинности Таблица истинности из задачи 1 1 1 1 Ответ: star
Программа будет вместо нас подбирать такую комбинацию переменных, которая правильно до заполнит таблицу истинности из условия задачи. Для этого мы будем использовать встроенные в библиотеку itertools функции product () и permutation (). Теория
product(“ Объект перебора ” – строка / список ; repeat = «число» ) - возвращает декартово произведение итерируемых объектов. Если указан аргумент repeat, то входные итерируемые объекты повторяются указанное количество раз. Иными словами product () позволяет перемещать объекты при условии того, что объекты могут повторяться. Пример работы: выведем все возможные комбинации 0 и 1 с повтором 3 a = list(product([0, 1], repeat=3)) print(a) Результат:
permutations(“ Объект перебора ” – строка / список ; r = «число» ) - возвращает все возможные перестановки итерируемого объекта с уникальным расположением элементов. Иными словами перестановка без повторений. Параметр r указывает на длину перестановки. Примечание – параметр r больше чем длина объекта перебора не может быть. Пример работы: выведем все комбинации перестановок без повторений чисел 0, 1, 2 с длиной перестановки 2 a = list(permutations([0, 1, 2], r=2)) print(a) Результат:
Импортируем необходимые функции из библиотеки и напишем функцию в которой запишем логическое выражение из условия задачи: from itertools import product, permutations def f (s, r, a, t): return (s or ( not r)) and ( not (r == a)) and t
В списке m перепишем нашу таблицу из задачи, где вместо пропусков будем писать x1, x2, x3 … xn, где n – кол-во пропусков в таблице. В нашем случаем 4 пропуска: m = ( ( 0, 1, x 1, 0, 1 ), (x 2, 1, 1, 0, 1 ), ( 1, x 3, 0, x 4, 1 ), ) 1 2 3 4 Место под сами буквы
Выше объявления переменной m напишем переборный цикл по x1, x2, x3, x4 – перебираем по кол-ву пропусков внутри таблицы из условия. Так как числа 0 и 1 в строке таблицы истинности могут повторяться, значит будем использовать product(): for x1, x2, x3, x4 in product([0, 1], repeat =4): m = ( ( 0, 1, x1, 0, 1 ), (x2, 1, 1, 0, 1 ), ( 1, x3, 0, x4, 1 ), ) repeat =4 так как кол-во иксов 4.
Когда мы составляли ручным способом таблицу истинности можно было заметить, что повторяющихся строк в ней не было и быть не должно. Чтобы учесть это, воспользуемся функцией set(). set () создаёт множество уникальных элементов. for x1, x2, x3, x4 in product([0, 1], repeat =4): m = ( ( 0, 1, x1, 0, 1 ), (x2, 1, 1, 0, 1 ), ( 1, x3, 0, x4, 1 ), ) if len (m) == len ( set (m)):
Напишем переборный цикл по нашим буквам s, a, r, t. Каждая буква должна использоваться всего один раз, поэтому используем permutation() : for x1, x2, x3, x4 in product([0, 1], repeat =4): m = ( ( 0, 1, x1, 0, 1 ), (x2, 1, 1, 0, 1 ), ( 1, x3, 0, x4, 1 ), ) if len (m) == len ( set (m)): for p in permutations( " srat ", r =4): r =4 так как кол-во букв 4.
Поясним некоторые функции: all() - возвращает True, если все элементы в итерируемом типе равны True. В остальных случаях возвращает False. print ( all ([1, 1, 1])) print ( all ([1, 1, 0])) zip() - объединяет элементы нескольких объектов (кортежей, списков, строк) в пары a = [ 's', 'r', 'a', 't' ] b = [ 0, 1, 0, 1 ] print ( list ( zip (a, b))) True False [('s', 0), ('r', 1), ('a', 0), ('t', 1)]
dict () - создаёт словарь — неупорядоченную, изменяемую и индексируемую коллекцию, которая хранит данные в формате пар «ключ — значение» a = [ 's', 'r', 'a', 't' ] b = [ 0, 1, 0, 1 ] print ( dict ( zip (a, b))) У нас получился словарь где буква это ключ, а значение – число 1 или 0. По такой логике мы будем перебирать наши буквы с цифры 0/1, которые находятся внутри переменных x1 … x4. Знак * перед списком / кортежем / множеством / словарём означает распаковку данных print ( * dict ( zip (a, b))) {'s': 0, 'r': 1, 'a': 0, 't': 1} s r a t Для словаря мы получили ключи
После переборного цикла permutations запишем следующую строчку кода: if all (f(** dict ( zip (p, x))) == x[- 1 ] for x in m): ** нужны чтобы передавать в функцию f не ключи (буквы s, a, r, t ), а числа (0, 1). Мы сравниваем, что функция f возвращает нам такое же число, что и последний элемент (-1 элемент) каждой строки переменной m – столбец F из таблицы истинности. Функция all говорит, что при всех x1, x2, x3, x4 функция f должна возвращать True ( -1 элемент ). Если это условие выполняется, то мы нашли нужную комбинацию букв s, a, r, t. Осталось её только вывести: print (p)
('s', 't', 'a', 'r')
8 Создаём пустое множество, чтобы избежать повторных комбинаций букв xywz, так как мы их перебираем внутри перебора product. Метод add добавляет элемент в конец множества
В классе решить тест https:// inf-ege.sdamgia.ru/emul/17589210/test Домашняя работа: на сайте https:// kompege.ru/course в разделе 6 задание 2 решить всю домашнюю работу. ВАЖНО!!! Если вы выбрали решать задачи способом 2, каждый раз с новой задачей полностью стирайте код и пишите его заново.
