Урок № 1 Повторение. Треугольники. План урока: 1 Вспоминаем теорию. 2 Решаем задачи. 3 ДЗ Умение мыслить математически – одна из благороднейших способностей человека. (Джордж Бернард Шоу )
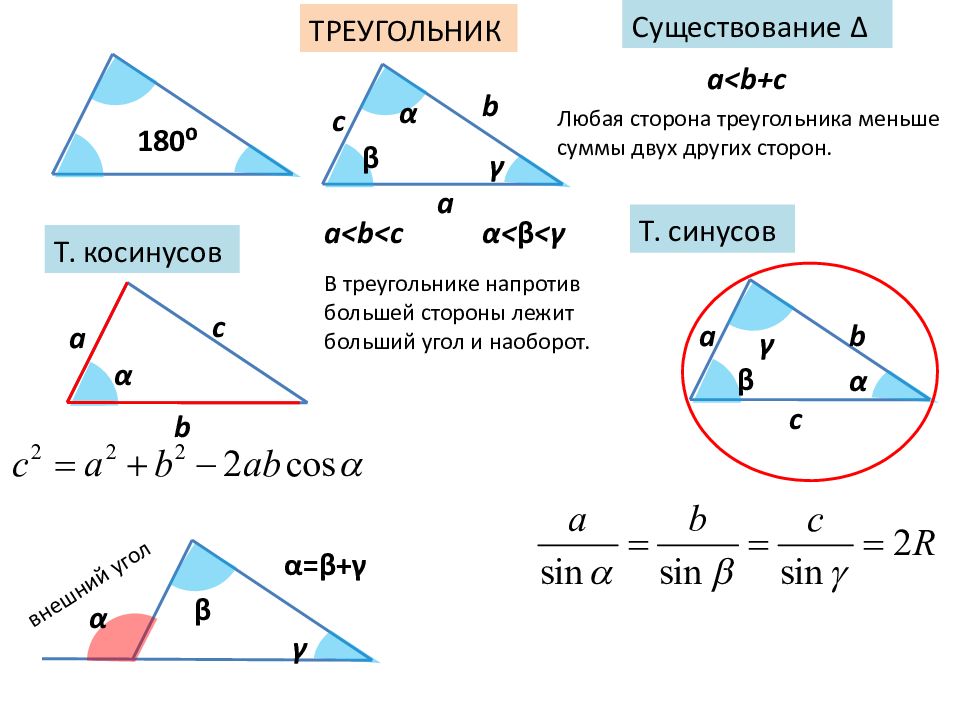
180 ⁰ a b c α Т. косинусов Т. синусов a α b β c γ Существование Δ a< b+c ТРЕУГОЛЬНИК a<b<c α < β < γ a α b β c γ внешний угол α = β + γ α β γ Любая сторона треугольника меньше суммы двух других сторон. В треугольнике напротив большей стороны лежит больший угол и наоборот.
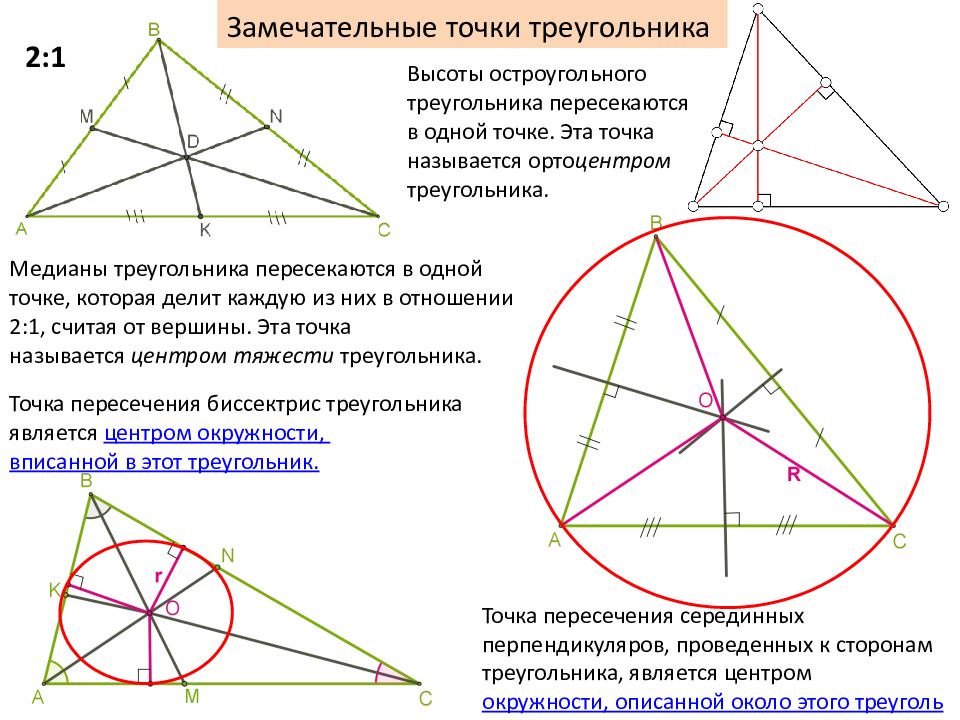
Замечательные точки треугольника 2:1 Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник. Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника. Высоты остроугольного треугольника пересекаются в одной точке. Эта точка называется орто центром треугольника.
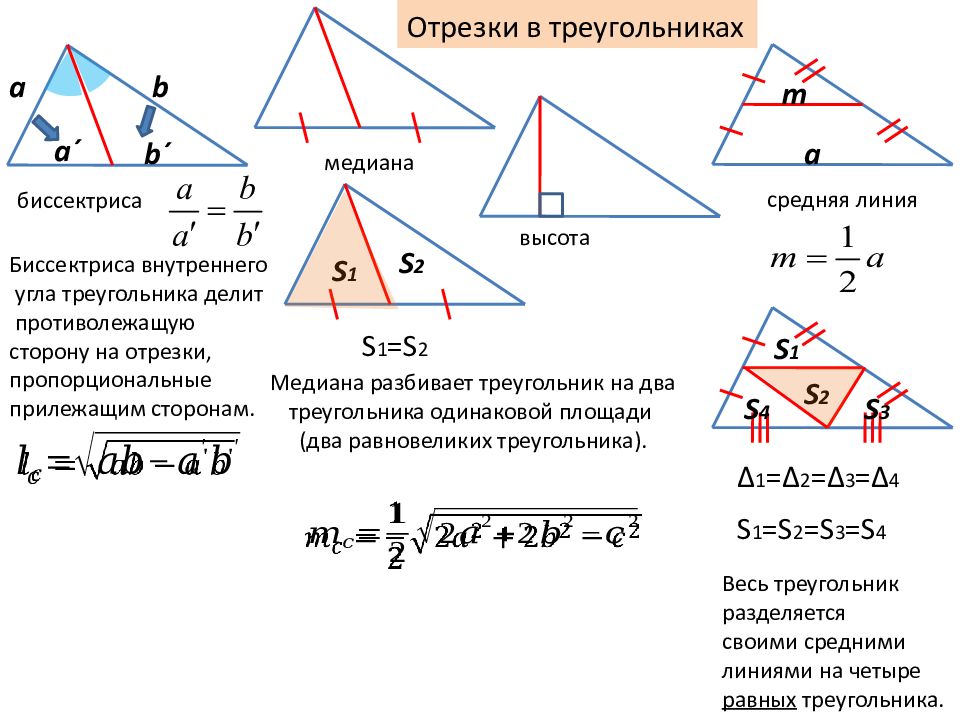
медиана высота средняя линия m a S 1 S 2 S 3 S 4 Δ 1 = Δ 2 = Δ 3 = Δ 4 S 1 =S 2 =S 3 =S 4 S 1 S 2 S 1 =S 2 Весь треугольник разделяется своими средними линиями на четыре равных треугольника. Отрезки в треугольниках Медиана разбивает треугольник на два треугольника одинаковой площади ( два равновеликих треугольника). Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. биссектриса a b a ´ b ´
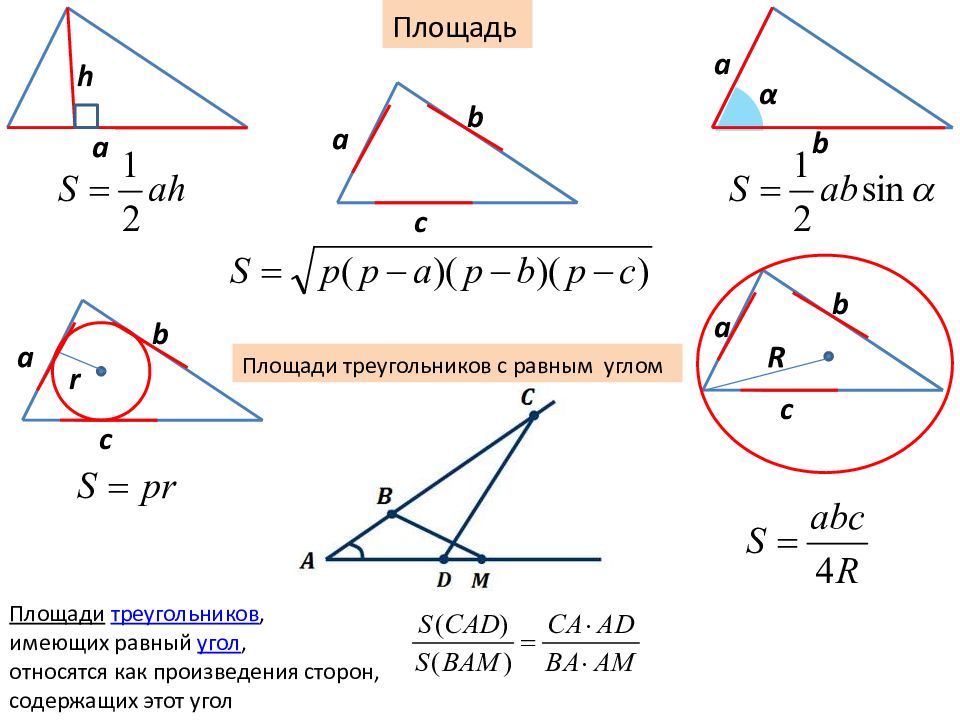
Площадь a a h b α a c b a c b R a c b r Площади треугольников с равным углом Площади треугольников, имеющих равный угол, относятся как произведения сторон, содержащих этот угол
Признаки равенства треугольников Признаки подобия треугольников
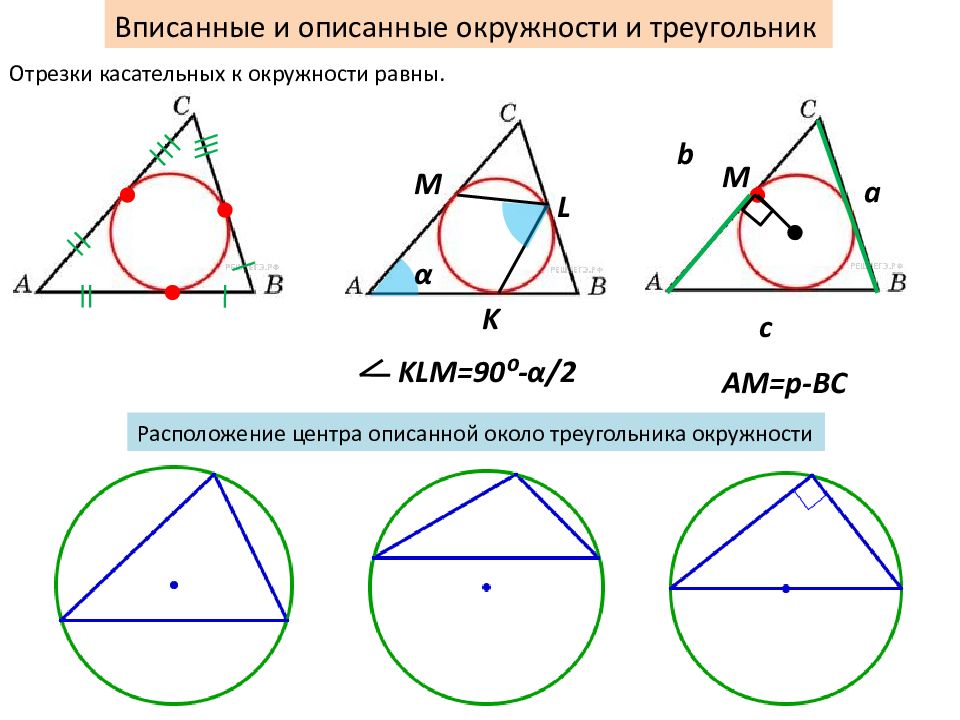
Вписанные и описанные окружности и треугольник Отрезки касательных к окружности равны. М АМ=р-ВС a b c K L М α KL М= 90 ⁰ - α /2 Расположение центра описанной около треугольника окружности
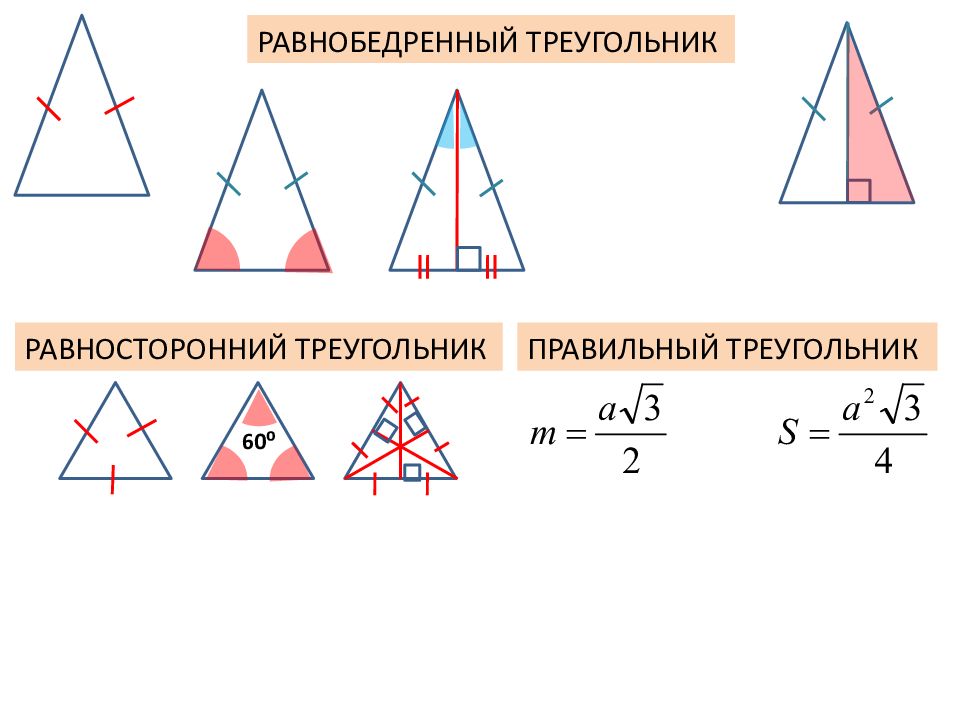
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК ПРАВИЛЬНЫЙ ТРЕУГОЛЬНИК 60 ⁰
Решение задач
Домашнее задание с урока 1: сайт «Решу ЕГЭ», треугольники позиция 1, выбор 10 задач и их решить
