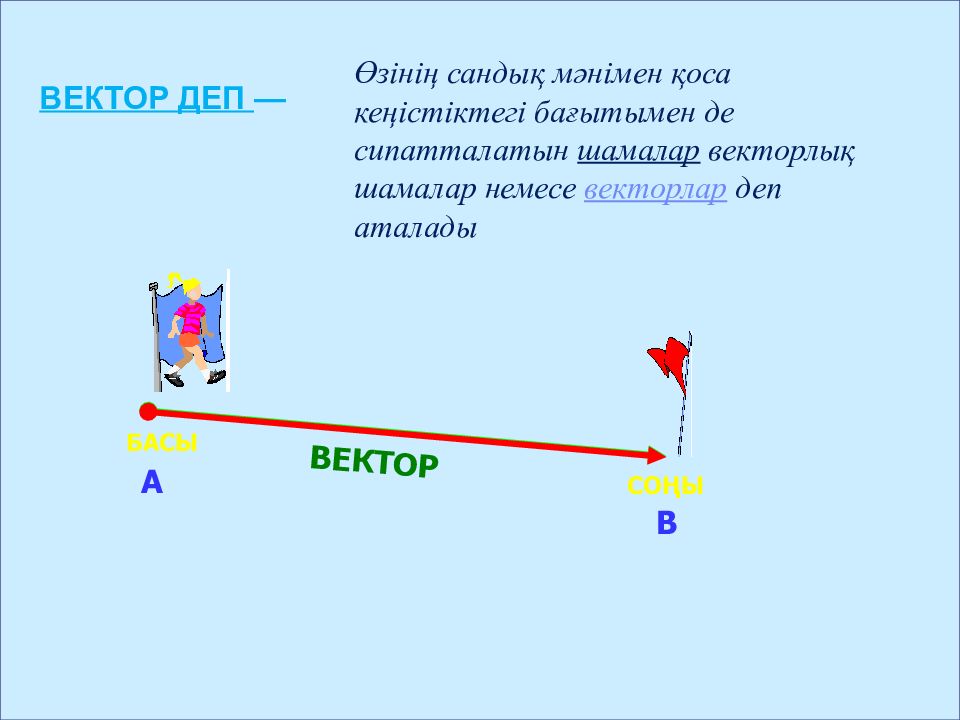
БАСЫ СОҢЫ А В ВЕКТОР ВЕКТОР ДЕП — Өзінің сандық мәнімен қоса кеңістіктегі бағытымен де сипатталатын шамалар векторлық шамалар немесе векторлар деп аталады
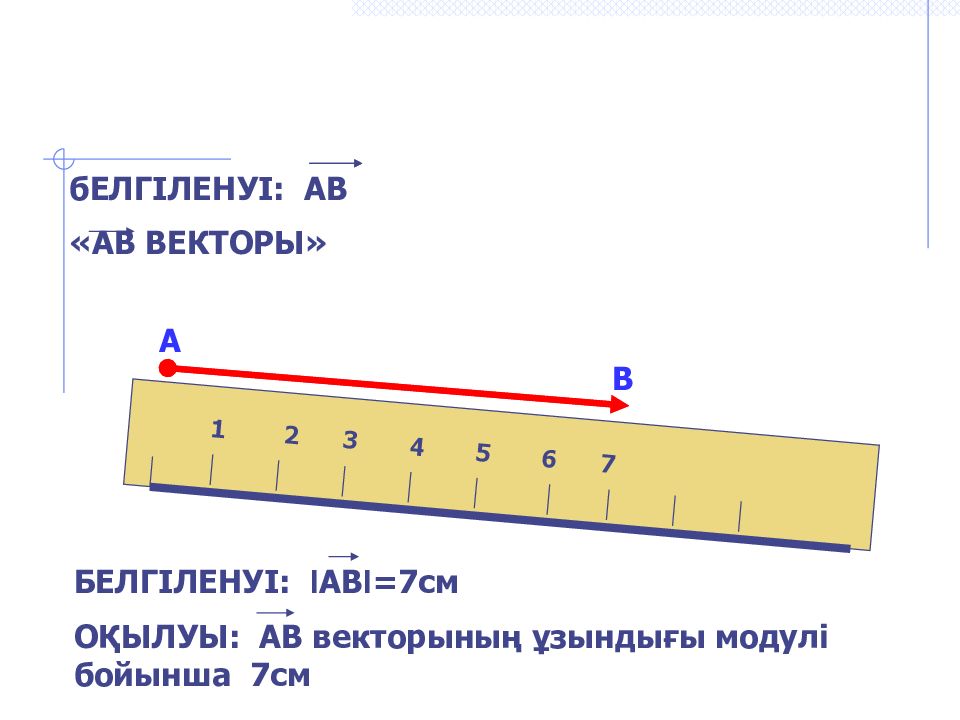
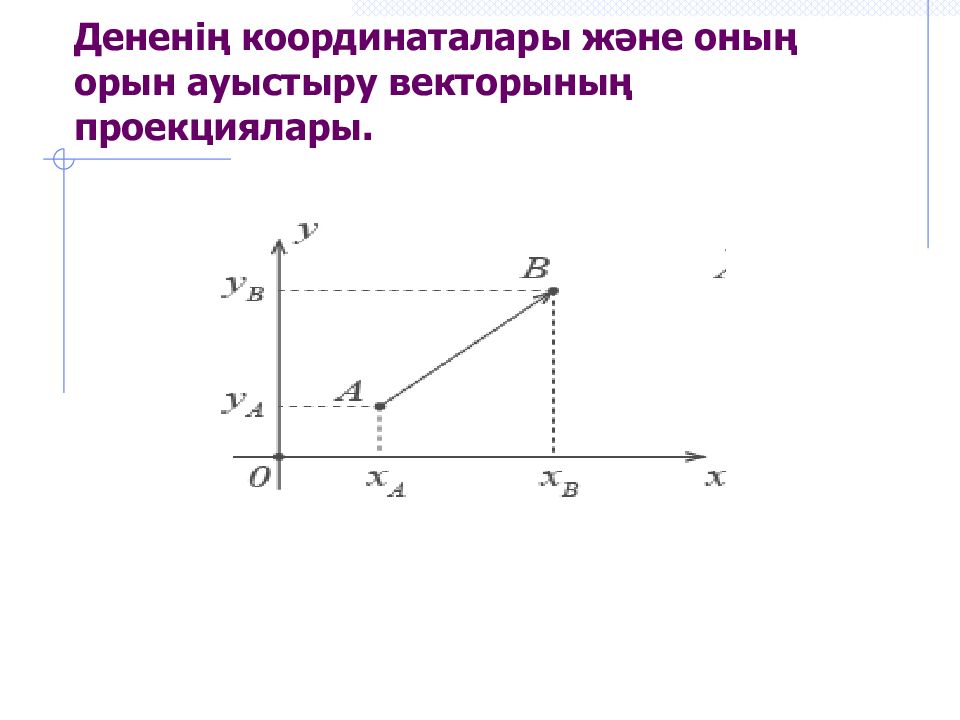
А В 1 2 3 4 5 6 7 бЕЛГІЛЕНУІ : АВ «АВ ВЕКТОРЫ» БЕЛГІЛЕНУІ: I АВ I =7c м О ҚЫЛУЫ : АВ векторының ұзындығы модулі бойынша 7см
а КОЛЛИНЕАР ВЕКТОР деп — Екі нөл емес (0-ге тең емес) векторлар параллель түзулерде немесе бір түзуде жатса коллинеа́р векторлар деп аталады b с d
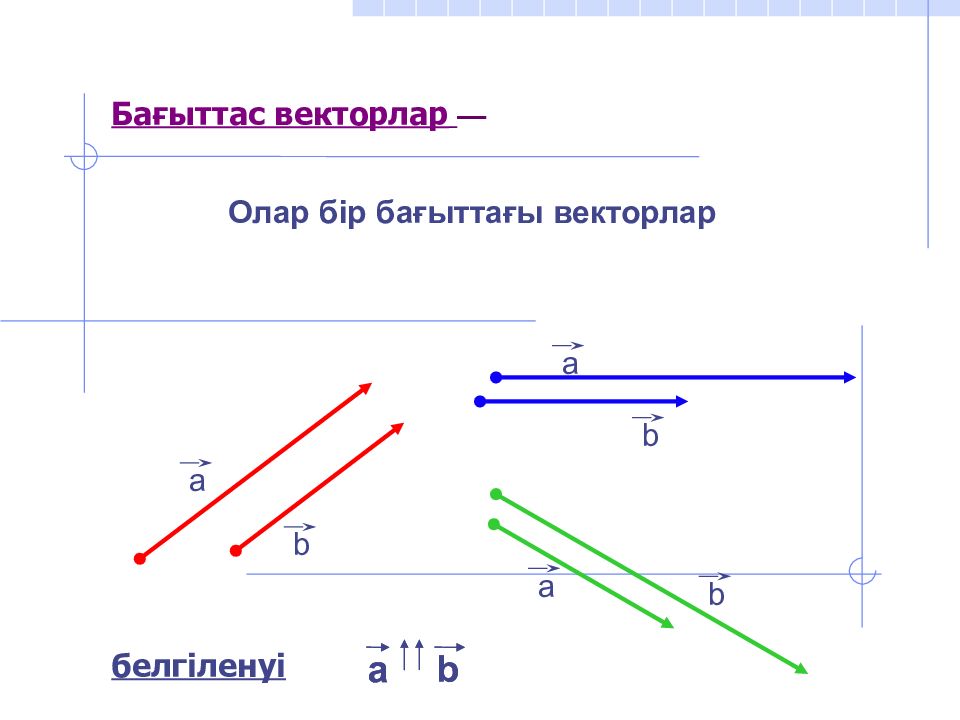
Олар бір бағыттағы векторлар а b а b а b Бағыттас векторлар — а b белгіленуі а b
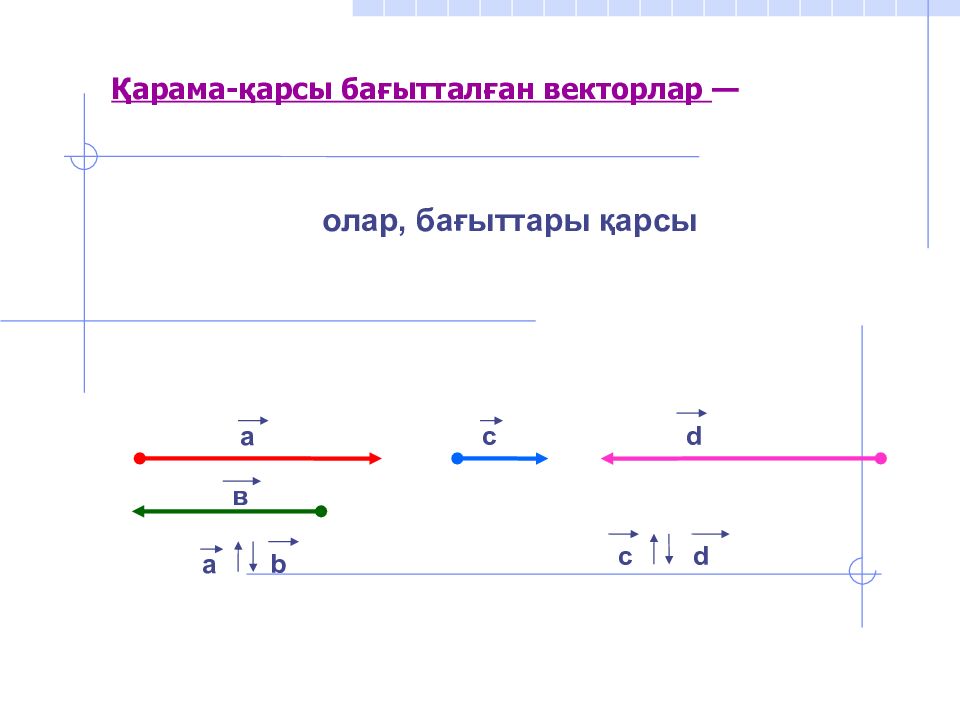
олар, бағыттары қарсы Қарама- қарсы бағытталған векторлар — а b а в с d с d
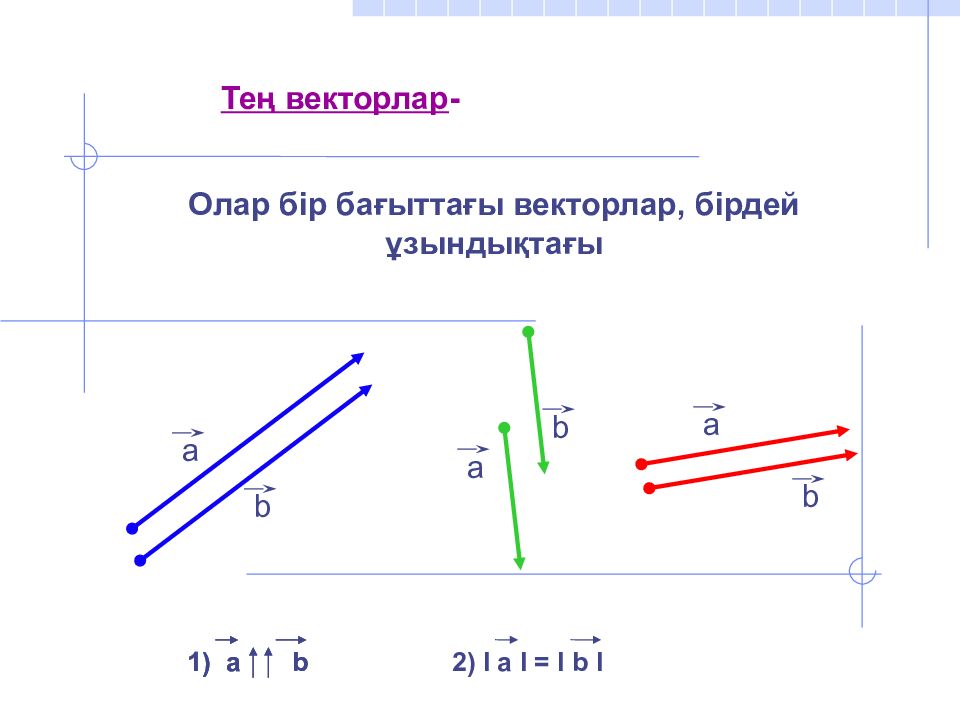
Олар бір бағыттағы векторлар, бірдей ұзындықтағы Тең векторлар - а b а b а b 2) I а I = I b I 1) а b 1) а b
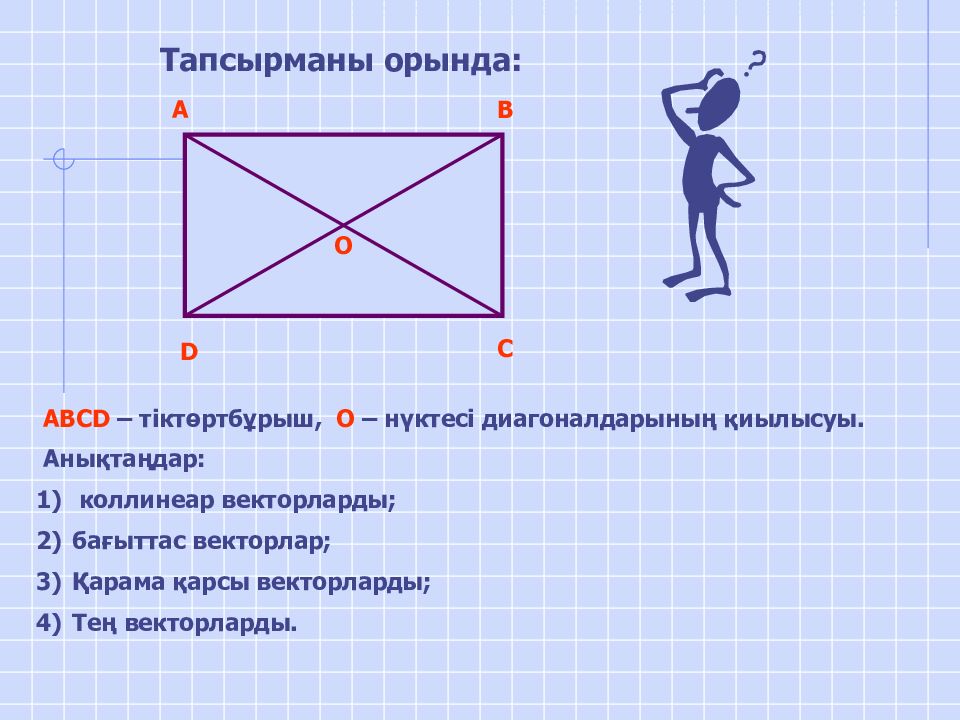
Тапсырманы орында: D A B C O ABCD – тіктөртбұрыш, О – нүктесі диагоналдарының қиылысуы. Анықтаңдар: коллинеар векторларды; бағыттас векторлар; Қарама қарсы векторларды; Тең векторларды.
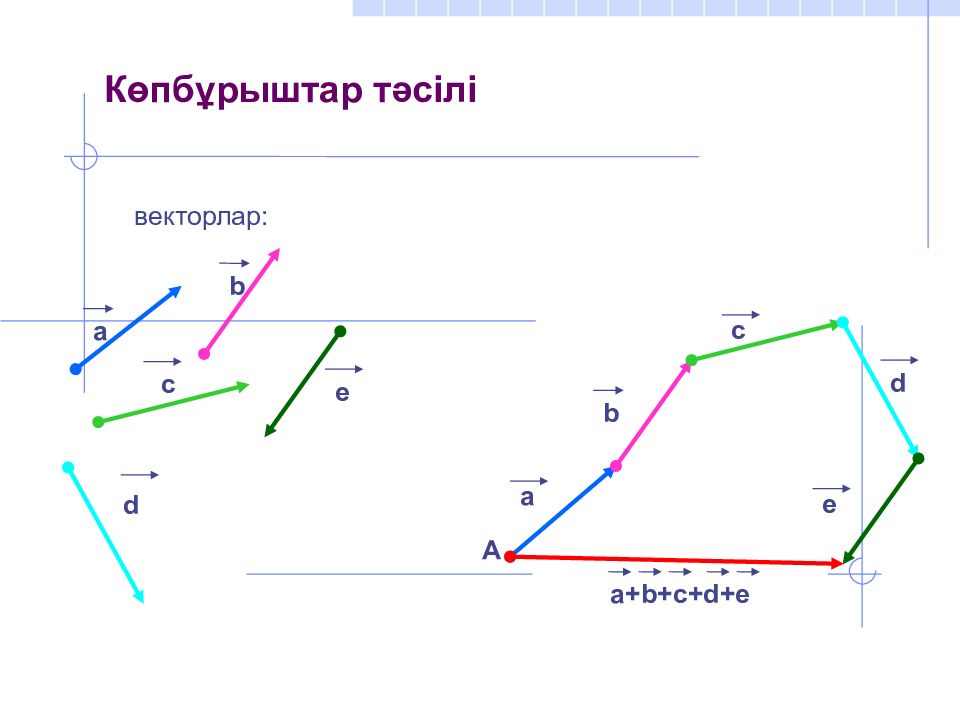
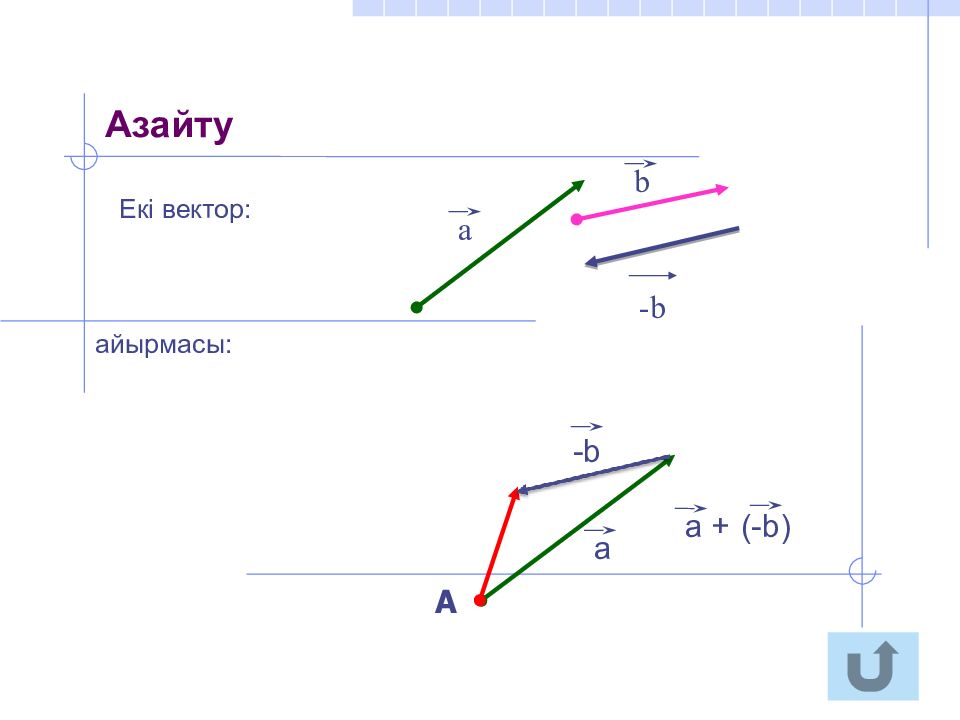
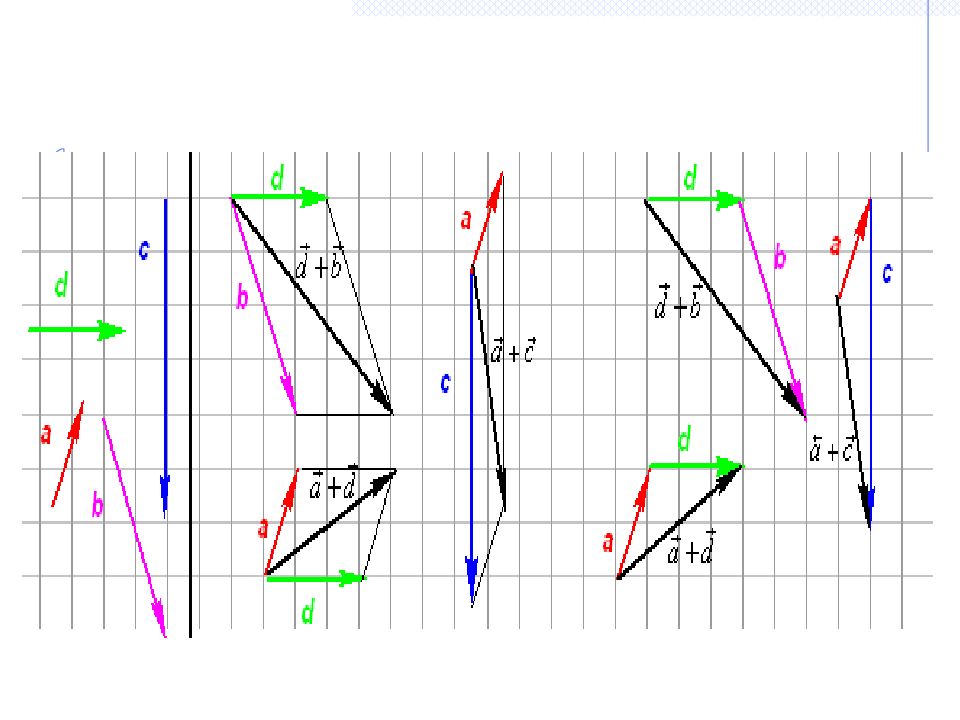
Үшбұрыштар тәсілі параллелограмдар ережесі векторларды азайту Векторларды көпбұрыштар ережесімен қосу векторларды скаляр шамаға көбейту және бөлу
ВЕКТОРларды қосу (үшбұрыштар) а b Екі вектор: қосу:
ВЕКТОРларды қосу (үшбұрыштар) а b а b а b + Екі вектор: қосу: А
. ВЕКТОРларды қосу ( параллелограм ережесі) Екі вектор: қосу: а b
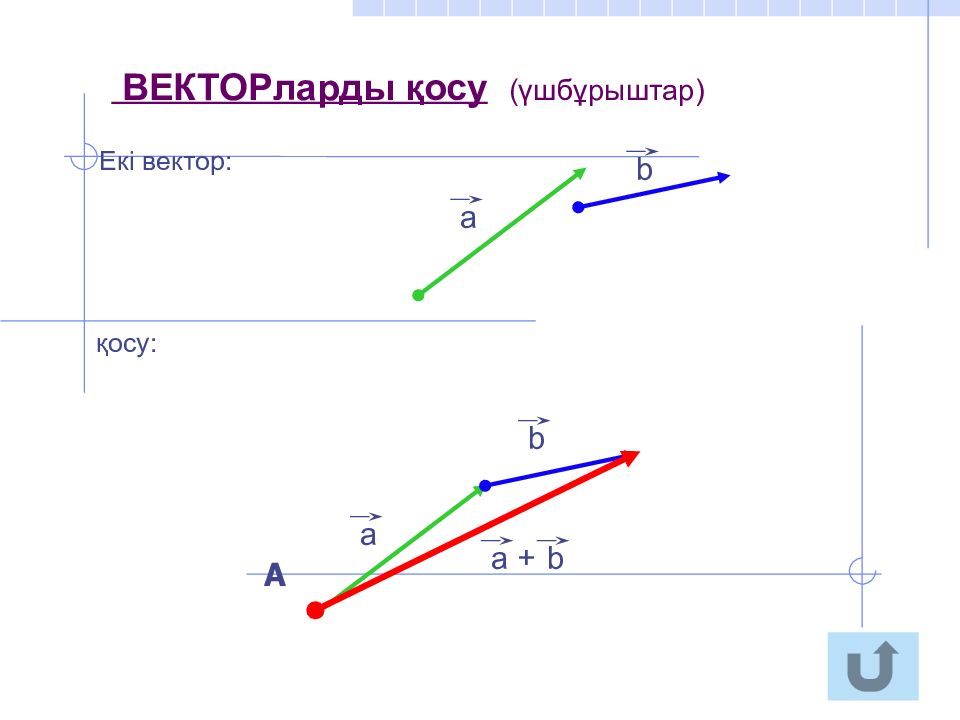
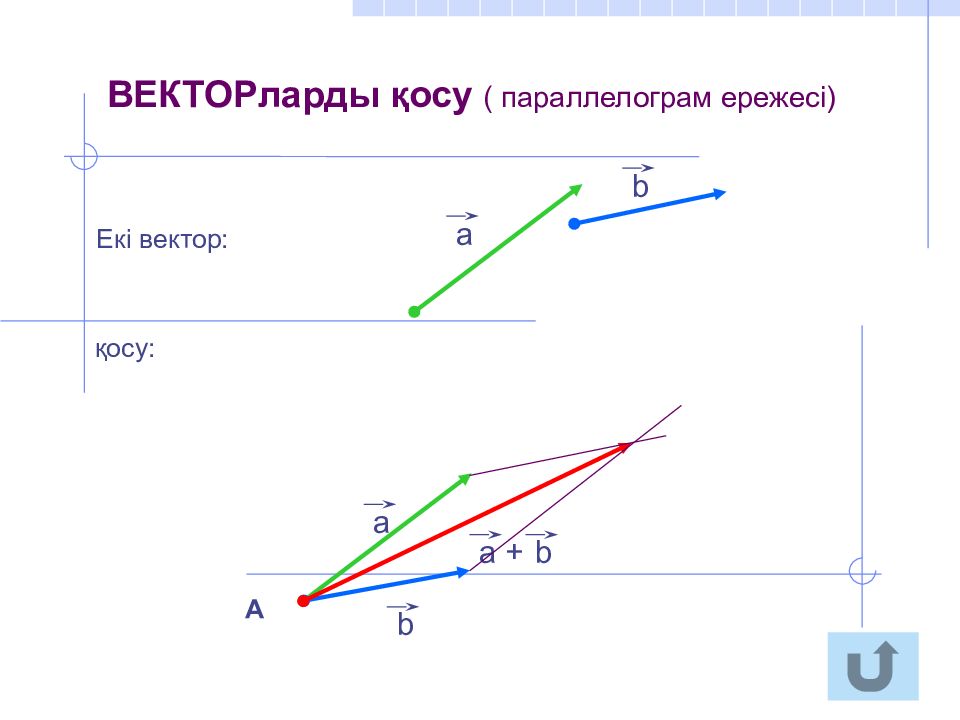
. ВЕКТОРларды қосу ( параллелограм ережесі) а b а b + Екі вектор: қосу: А а b
Көпбұрыштар тәсілі векторлар: A. с d e a b a b с d e a+b+c+d+e
Азайту а -b а (- b ) + Екі вектор: айырмасы: а b А - b
А. Скаляр шамаға көбейту және бөлу а 0,5а В. 2 а С. а -а вектор
Вектордың координаталар осьтеріндегі проекциялары
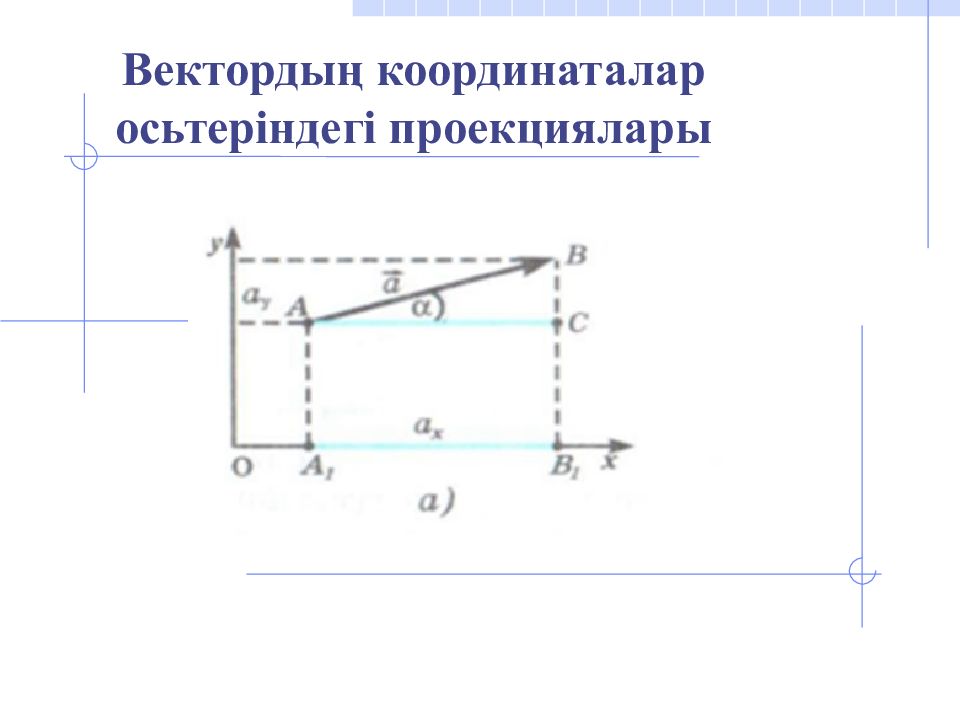
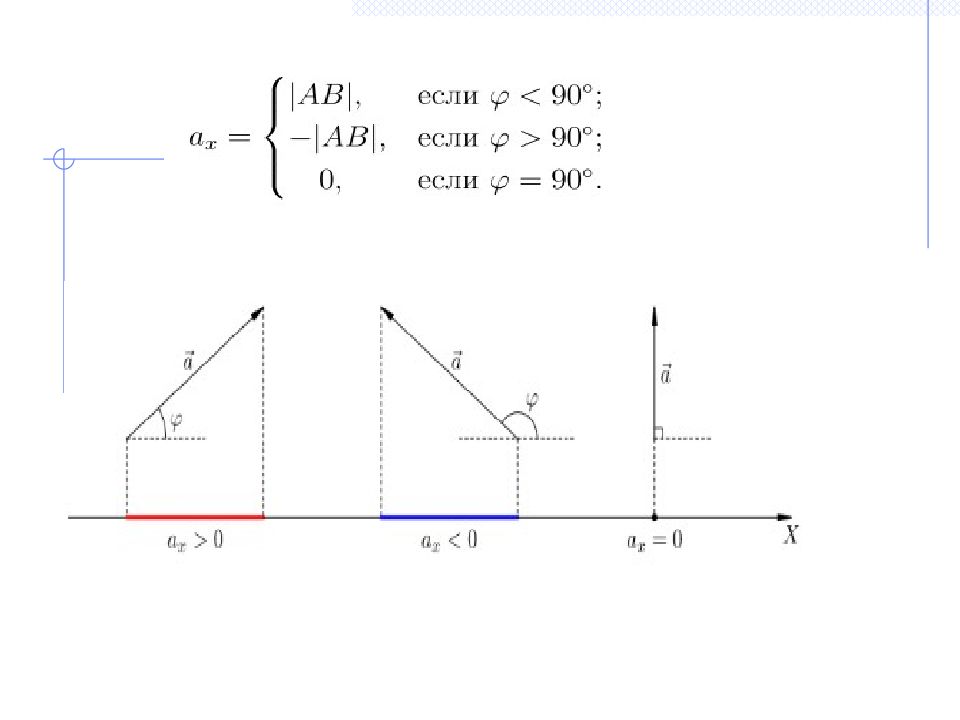
Проекциялардың таңбаларын анықтау үшін мына қарапайым ережені пайдаланамыз. Егер вектордың бас нүктесінің проекциясынан оның ұшының проекциясына қарай ось бағытымен жүретін болсақ, онда проекция оң, ал қарама – қарсы бағытта жүретін болсақ теріс болады.
Векторлар қосындысының бір осьтегі проекциясы қосылатын векторлардың сол осьтегі проекцияларының алгебралық қосындысына тең
