«Вероятность события»
В результате бросания любой монеты ( это испытание ) обязательно произойдет одно из двух событий : выпала «решка» или выпал «орел». Событие -любое явление, которое происходит или не происходит Событие -результаты испытаний (опытов), наблюдений и измерений, производимых людьми
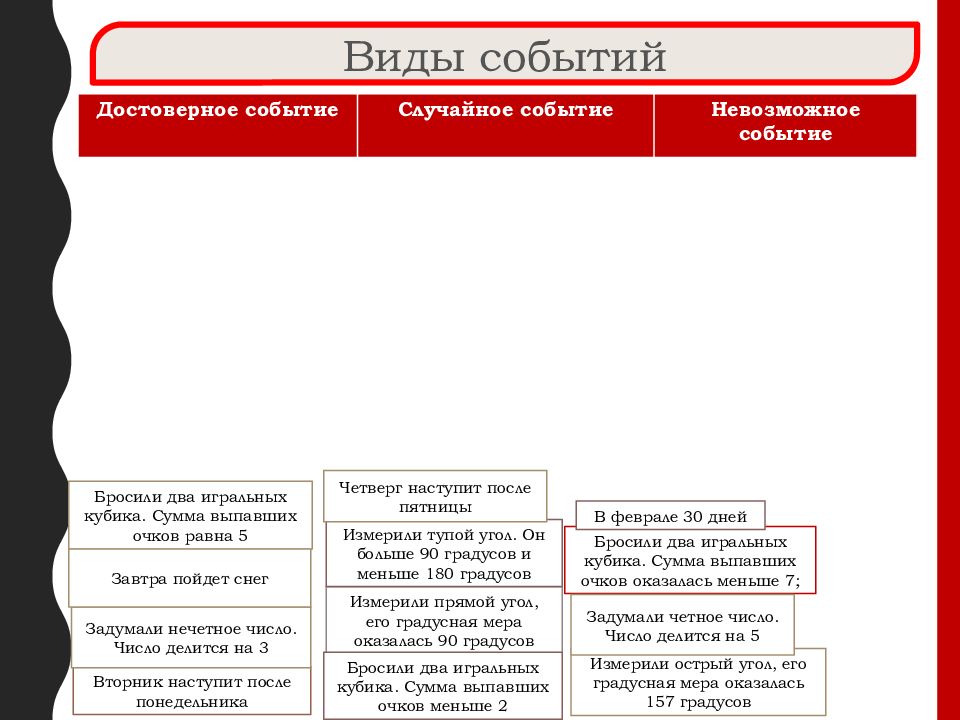
Достоверное событие Случайное событие Невозможное событие Виды событий Вторник наступит после понедельника Измерили острый угол, его градусная мера оказалась 157 градусов Бросили два игральных кубика. Сумма выпавших очков оказалась меньше 7; Измерили прямой угол, его градусная мера оказалась 90 градусов Измерили тупой угол. Он больше 90 градусов и меньше 180 градусов Бросили два игральных кубика. Сумма выпавших очков равна 5 Четверг наступит после пятницы Задумали нечетное число. Число делится на 3 Задумали четное число. Число делится на 5 Завтра пойдет снег В феврале 30 дней Бросили два игральных кубика. Сумма выпавших очков меньше 2
Совместные и не совместные события Бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков Пошел дождь; наступило утро Наступило день; наступила ночь Бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем.
Равновозможные и неравновозможные события Появление «орла» и появление «решки» при одном бросании монеты При бросании игральной кости появление каждой из её граней Появление карты определённой масти при изъятии одной карты из колоды Падение бутерброда маслом вниз и падение бутерброда маслом вверх Выпадение любого числа очков от 1 до 6 при бросании игрального кубика
Встречаясь в жизни с различными событиями, мы часто даем оценку степени их достоверности. При этом произносим. Например, такие слова: «Это невероятно» - говорим мы о том, что вода в холодильнике закипела «Маловероятно, что сегодня будет идти дождь» - говорим, глядя на безоблачное небо летним утром
Одни случайные события происходят чаще, другие реже. Те события, которые происходят чаще, имеют большую возможность появления, а те которые реже – меньшую. Каждое случайное событие имеет свою меру возможности появления случайного события – вероятность. Она может быть выражена числом. Это определение вероятности.
Теория вероятностей - это математическая наука, изучающая закономерности в массовых случайных явлениях.
Долю успеха того или иного события математики называют вероятностью этого события (от латинского probabilitas – «вероятность»)
Что такое вероятность события? Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д. Событие А – выпала «решка» Событие В – выпал «орёл» Пример. Вероятностью события А называют отношение количества случаев, БЛАГОПРИЯТСТВУЮЩИХ событию А, к числу всех РАВНОВОЗМОЖНЫХ случаев, один из которых обязательно произойдет. где Р(А) –вероятность события А, m - количество БЛАГОПРИЯТСТВУЮЩИХ случаев, n - количество РАВНОВОЗМОЖНЫХ случаев. Р(А) = Если эксперимент, в котором появляется событие А, имеет конечное число n равновозможных исходов, вероятность события А равна где m - количество исходов, при которых событие А появляется.
Читают: «вероятность события А равна 0,88» Р(А) Задача: На экзамене 25 билетов, Сергей выучил 22 из них. Найдите вероятность того, что ему попадётся выученный билет. Дано: m=22 n=25 Р(А ) = ? Решение: Р(А) = Р(А) = Ответ: 0,88
Помимо рассмотренных элементарных событий можно рассматривать и более сложные события. Например, «выпадение четного числа очков при одном бросании игральной кости» Это событие наступает в трех случаях – когда выпадет 2, или 4, или 6 очков. Все эти исходы благоприятствуют событию А, тогда Дано: m= 3 n= 6 Р(А) = ? Решение: Р(А) = Р(А) Ответ: 0,5
Найти вероятность появления при одном бросании кости числа очков, большего 4 Событию А – «появление числа очков, большего 4», благоприятствуют 2 исхода (появление 5 или 6 очков), Дано: m= 2 n= 6 Р(А) = ? Решение: Р(А) = Р(А) Ответ:
Если событие А - достоверное, то ему благоприятствуют все возможные исходы испытания, т. e. m = n, тогда Р(А)= 1 Свойства Если событие А – невозможное, то не существует исходов благоприятствующих его появлению т. e. m = 0, тогда Р(А ) = 0 Если событие А – случайное, то число m благоприятствующих его появлению исходов удовлетворяет условию 0 < m < n, тогда 0 < Р(А) = < 1 0 ≤ P(A) ≤ 1
1. Коля выбирает двухзначное число. Найдите вероятность того, что оно делится на 30. 2.Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет. 3. На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. 4. В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси. 5. В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке. 6. Миша с папой решили покататься на колесе обозрения. Всего на колесе двадцать четыре кабинки, из них 5 — синие, 7 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Миша прокатится в красной кабинке. Решение задач
Даже если мы и может оценить вероятность события верно, то, скорее всего, крайне неточно, что не будет иметь никакого смысла, скажем, в космической инженерии, где миллионные доли решают многое. А когда нам нужна точность, то мы обращаемся к кому? Конечно же, к математике. Все мы в той или иной мере используем теорию вероятности, на основе анализе произошедших в нашей жизни событий. Мы знаем, что смерть во время автомобильной аварии боле вероятна, чем от удара молнии, потому что первое, к сожалению, происходит очень часто. Так или иначе мы обращаем на вероятность вещей внимание, чтобы спрогнозировать свое поведение. Но вот обида, к сожалению, не всегда человек может точно определить вероятность тех или иных событий Например, не зная статистики, большинство людей склонны думать, что шанс погибнуть в авиакатастрофе больше, чем в автомобильной аварии. Изучив факты можно убедиться, что это совсем не так.
Возможности теракта в метрополитене, экономического кризиса или ядерной войны — все это можно выразить в процентах. А главное, предпринимать соответствующие контрдействия исходя из полученных данных. Любую деятельность любой сферы можно проанализировать, использую статистику, рассчитать благодаря теории вероятности и заметно улучшить. Примеров реального использования теории вероятности в жизни множество. Практически вся современная экономика базируется на ней. Выпуская на рынок определенный товар, грамотный предприниматель наверняка учтет риски, а также вероятности покупки в том или рынке, стране и т.д. Практически не представляют свою жизнь без теории вероятности брокеры на мировых рынках. Предсказывание денежного курса (в котором точно не обойтись без теории вероятности) на денежных аукционах или знаменитейшем рынке Forex дает возможность зарабатывать на данной теории серьезные деньги. Теория вероятности имеет значение в начале практически любой деятельности, а также ее регулирования. Благодаря оценке шансов той или иной неполадки (например, космического корабля), мы знаем, какие усилия нам нужно приложить, что именно проверить, что вообще ожидать в тысячи километров от Земли.
Где встречается теория вероятностей В играх: Орел или решка кости лотерея карточные игры игровые автоматы На экзамене Например на ОГЭ угадывание правильного ответа
Теория вероятности имеет широкое применение: для прогнозирования погоды, для покупки исправных автомобилей, также для покупки исправных лампочек и разное другое.. На примере можно сделать и более общие выводы: подальше держаться от всяких лотерей, казино, карт, азартных игр вообще. Всегда надо подумать, оценить степень риска, выбрать наилучший из возможных вариантов – это пригодится и в дальнейшей жизни. В результате урока выявлено: Теория вероятностей - это огромный раздел науки математики и сфера его применения очень разнообразна. Перебрав множество фактов из жизни, и проведя эксперименты, с помощью теории вероятностей можно предсказать события, происходящие в различных сферах жизнедеятельности; Теория вероятностей - это целая наука, которой, казалось бы, нет места для математики, – какие уж законы в царстве Случая? Но и здесь наука обнаружила интересные закономерности. Если подбросить монету, то нельзя точно сказать, какой стороной она ляжет вверх – гербом или цифрой. Но проведя испытания, оказывается, что при многократном повторении опыта частота события принимает значения, близкие к 0,5.
