ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР С ПОМОЩЬЮ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
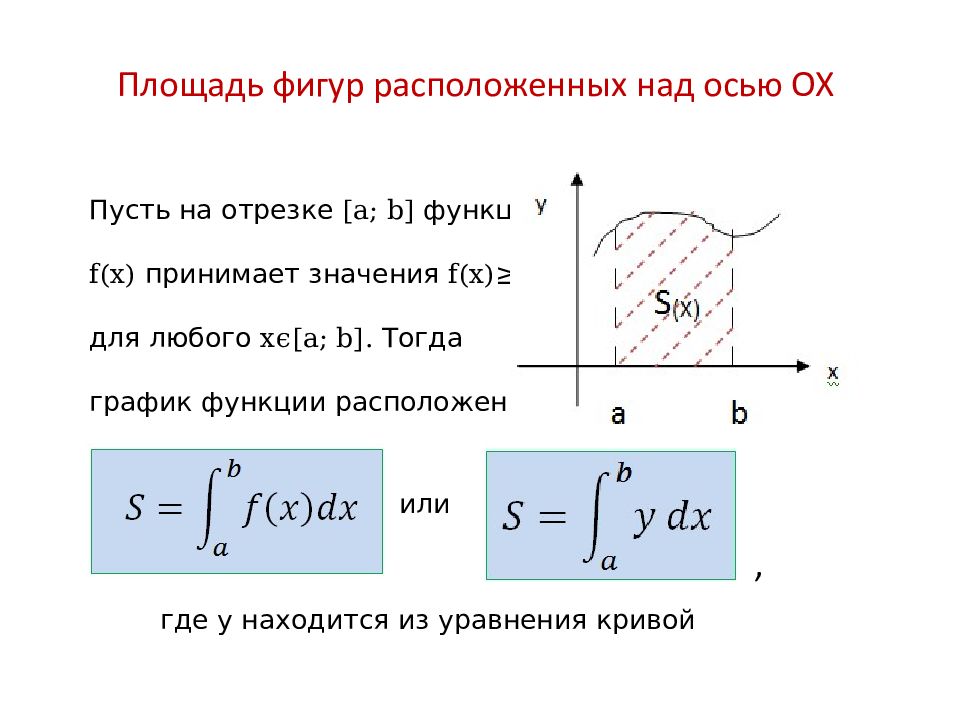
Площадь фигур расположенных над осью ОХ Пусть на отрезке [ a; b] функция f(x) принимает значения f(x)≥ 0 для любого x ϵ[ a; b]. Тогда график функции расположен над осью Ох. или где у находится из уравнения кривой ,
Площадь фигур расположенных под осью ОХ Пусть на отрезке [ a; b] задана непрерывная функция y=f(x), f(x)≤ 0. Тогда график функции расположен под осью Ох. или , где у находится из уравнения кривой.
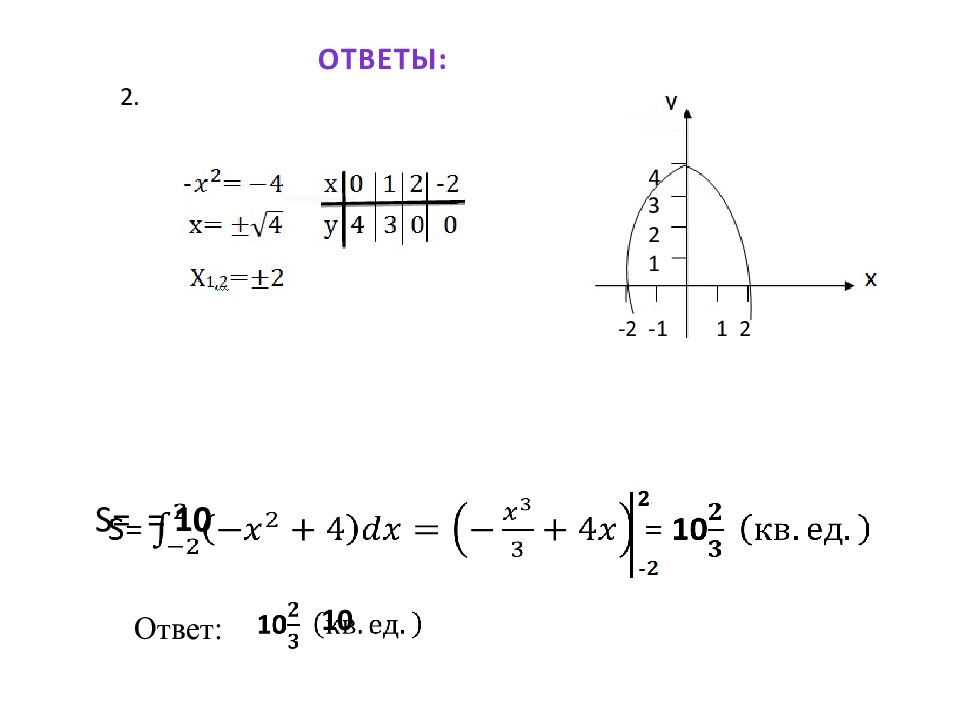
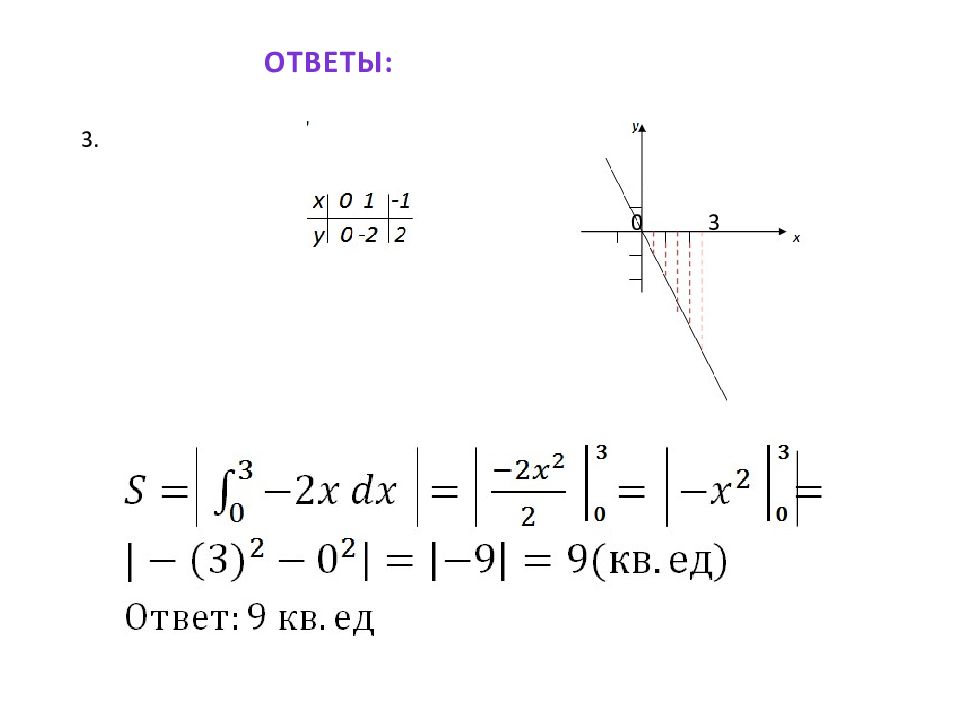
Алгоритм вычисления площадей плоских фигур: По условию задачи делают схематический чертёж; Представляют искомую площадь, как сумму или разность площадей криволинейных трапеций. Из условия задачи и чертежа определяют пределы интегрирования для каждой составляющей криволинейной трапеции. Записывают каждую функцию в виде у= f (х). Вычисляют площади каждой криволинейной трапеции и площадь искомой фигуры.
ПРИМЕРЫ: Вычислите площади фигур, ограниченных заданными линиями:
Ответы: 1. Для любого х, функция y = п оложительные значения. 16 25 S= 25 16 Ответ: 122 кв.ед.
Ответы: 4 3 2 1 -2 -1 1 2 2. S= = 10 Ответ: 10
ПРИМЕРЫ: 3.Вычислите площадь фигуры, ограниченной заданными линиями:
Ответы: 3 0 3.
РЕШИТЕ САМОСТОЯТЕЛЬНО: Вычислите площади фигур, ограниченных заданными линиями: , . и
ПРОВЕРЬТЕ ОТВЕТЫ: 2 (кв. ед.) 8(кв. ед.)
