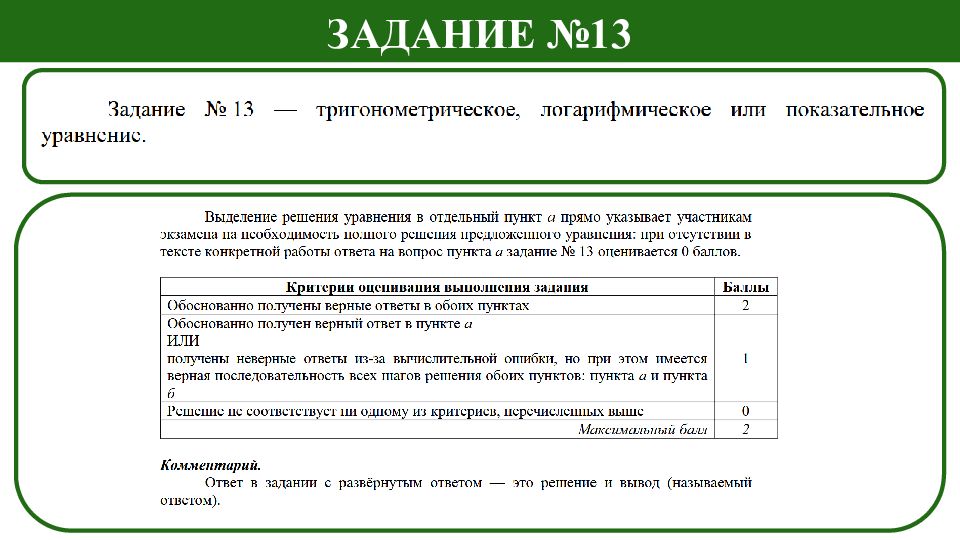
Слайд 3: Задание №13
Форма записи группы корней может быть различной. Арифметическими считаются только ошибки при выполнении четырех арифметических действий (сложения, вычитания, умножения, деления). Любые ошибки, допущенные в тригонометрических формулах, в нахождении значений тригонометрических функций, при использовании свойств неравенств не относятся к вычислительным.
Слайд 4: Отбор корней с помощью перебора
При отборе корней с помощью перебора надо доказать, что другие корни, кроме указанных, не удовлетворяют условию. Отбор корней нельзя назвать обоснованным, если перебор остановлен на корне, принадлежащем отрезку, или если указаны только корни, принадлежащие отрезку. При отборе корней с помощью перебора должен быть показан корень, который ЕЩЕ не входит в промежуток, корни промежутка и корень, который УЖЕ не входит в промежуток.
Слайд 9: 13
Обоснованно получен ответ в пункте а. При решении квадратного уравнения есть неточность в записи дискриминанта. Отбор корней нельзя считать обоснованным, так как отбор корней остановлен на корне, принадлежащем промежутку. 1 балл
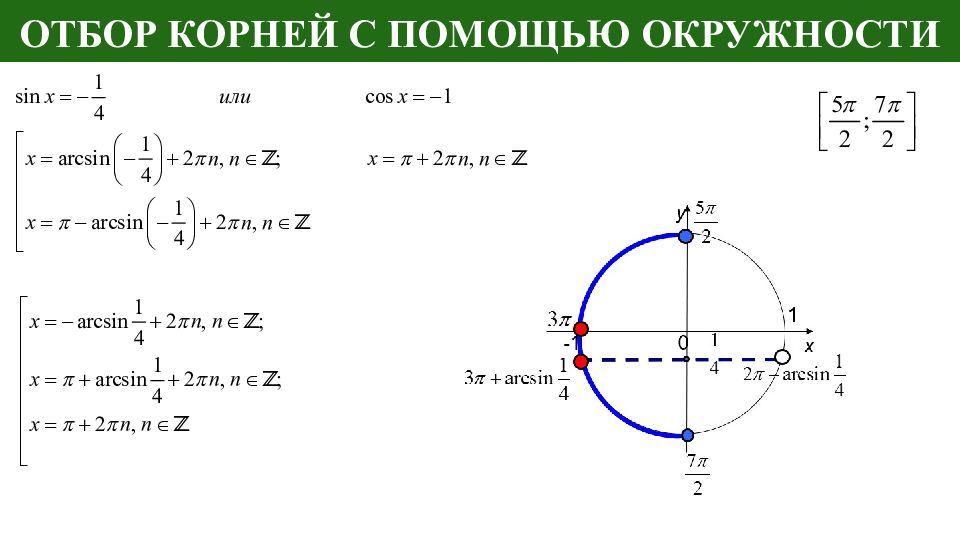
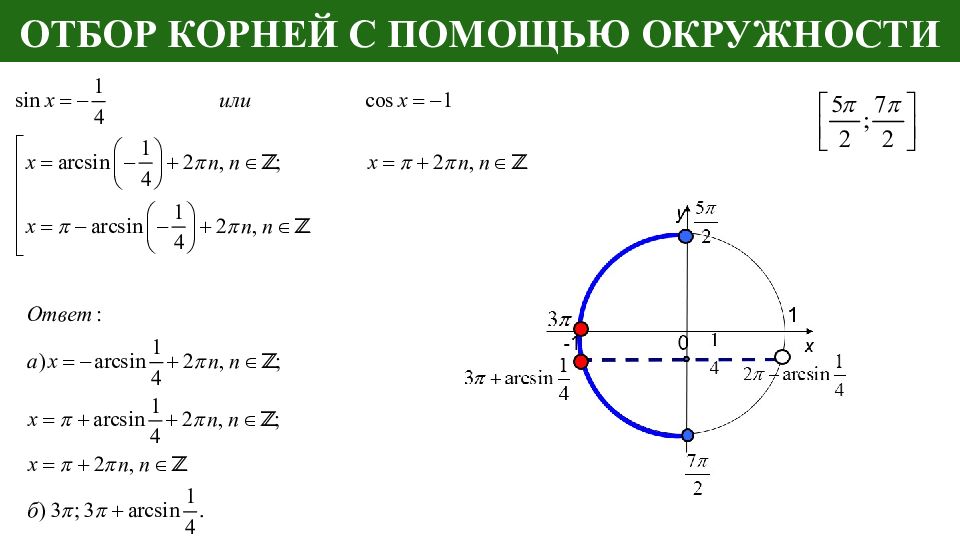
Слайд 10: Отбор корней с помощью окружности
На числовой окружности должно быть: отмечены и обозначены концы промежутка; выделена дуга, соответствующая рассматриваемому промежутку (каким-то образом); на окружности отмечены и подписаны корни, принадлежащие данному отрезку. Оси х и у подписывать не нужно
Слайд 15: Отбор корней с помощью окружности
Обоснованно получен верный ответ в пункте а. Отбор корней с помощью тригонометрической окружности неверный, так как на отмеченной дуге отмечен корень, не принадлежащий числовому отрезку. 1 балл
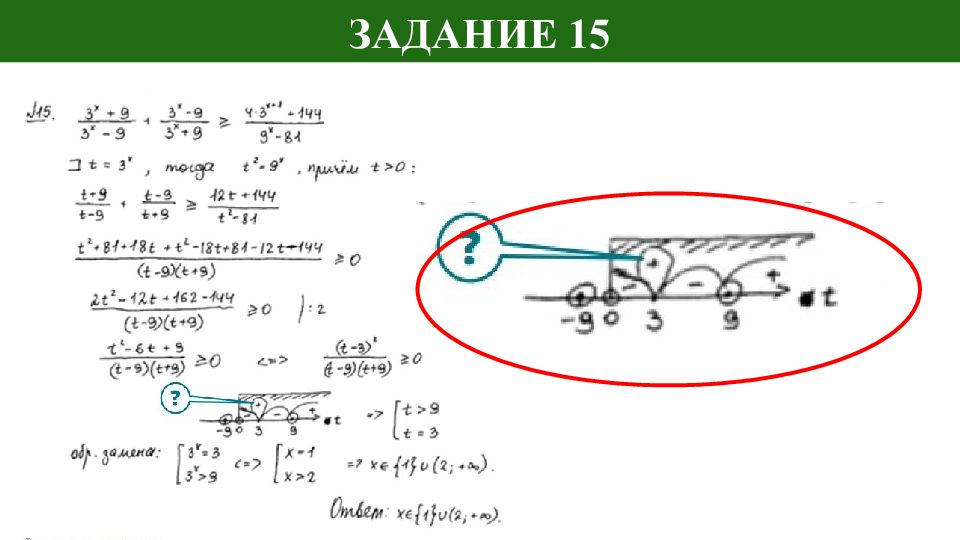
Слайд 18: Отбор корней с помощью неравенства
Необходимо внимательно выполнять все вычисления, каждый шаг преобразований. Ошибка, даже при наличии правильного ответа, не позволяет поставить балл за пункт б.