В Системных З наниях практически всё рассматривается с системных позиций, при этом каждая система базируется на структурах энергетических решёток, построенных из различных платоновых тел. Вот пространство А, которое мы рассматриваем, оно о грани чено, т.к. это какая-то структура в N - мерном пространстве. Структура у нас единая, изначальная, т.е. АЗ овая, поэтому будем обозначать её | а | — « азъ », она будет передавать любую структуру и отображать любую проекцию, как в х ’ Арийской арифметике.
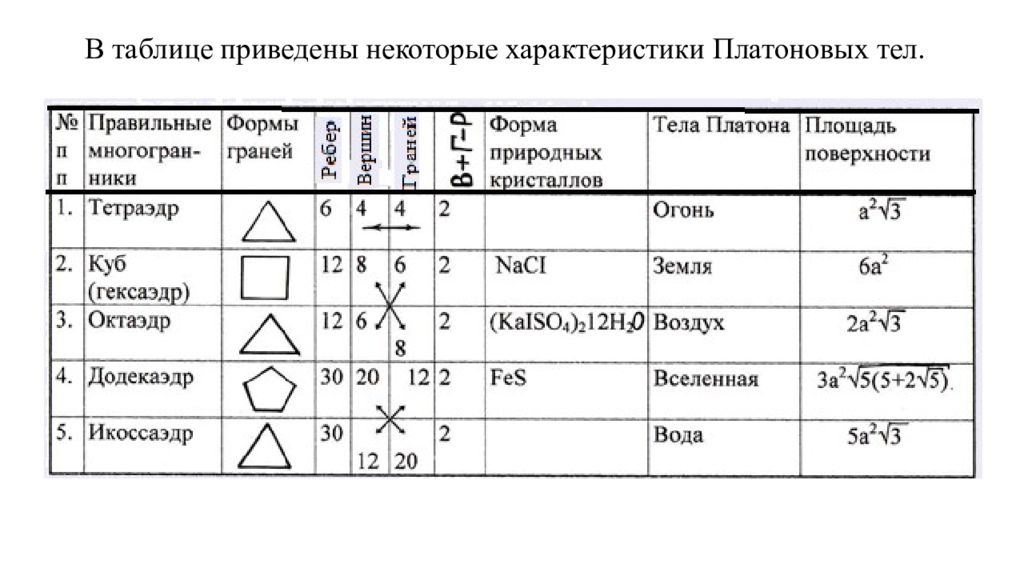
Здесь мы имеем дело с триадной системой (это может быть тетраэдр гармоний, квантон (из теории суперобъединения Леонова), октаэдр – 6 опорных точек, икосаэдр – 12 опорных точек, додекаэдр – 20 опорных точек, октаэдр – их 8, т.е. это всё определённое законами Яви. Поэтому это всё трёхмерное и любое действие, которое мы будем производить, оно тоже будет последовательно идти во времени. Но мы как бы считаем определённые пространственные характеристики. В основании каждой структуры лежит определённое количество опорных точек. Например, линия – одномерная структура, двумерная структура, имеет три опорые точки ; тетраэдр - это трёхмерная структура, имеет четыре опорные точки, которые находятся в вершинах пирамиды.
Перед нами ПЯТЬ Платоновых тел, которые могут быть вложены каждая в последующую, образуя в целом сложную структуру. Из них (см. рис) возможно формирование разных частиц от предатомарного уровня мерной масштабности до масштабов Вселенной. При этом структурно в их узлах могут располагаться электрические частицы – фотоны, а вдоль рёбер – бинарные магнитные частицы, и наоборот: в узлах магнитные частицы, а вдоль граней фотоны, что создаёт разнообразие структур частиц.
В таблице приведены некоторые характеристики Платоновых тел.
Ибо, как говорят: чтобы человека не путать со временем, детям объясняют просто: вот эти четыре луча ( Х ), это глубина, длина, ширина и высота. Но понятие ширина и длина у славян взаимосвязано. Я смотрю в эту сторону (т.е. прямо), вот для меня длина, вот ширина (указывая рукой направо). Я повернулся направо – они поменялись местами. Т.е. это что? - плавно перетекающие структурные характеристики. Т.е. частицы не просто соприкоснулись, они соответствуют друг другу, между собой могут также и взаимодействовать, что означается знаком взаимодействие соответствий, см. табл. 2 (в обычной математике этого нет). Например, два одинаковых плоских магнита могут притягиваться друг к другу разными полюсами благодаря магнитному полю обоих магнитов. Этот знак означает совместимость взаимодействующих элементов.
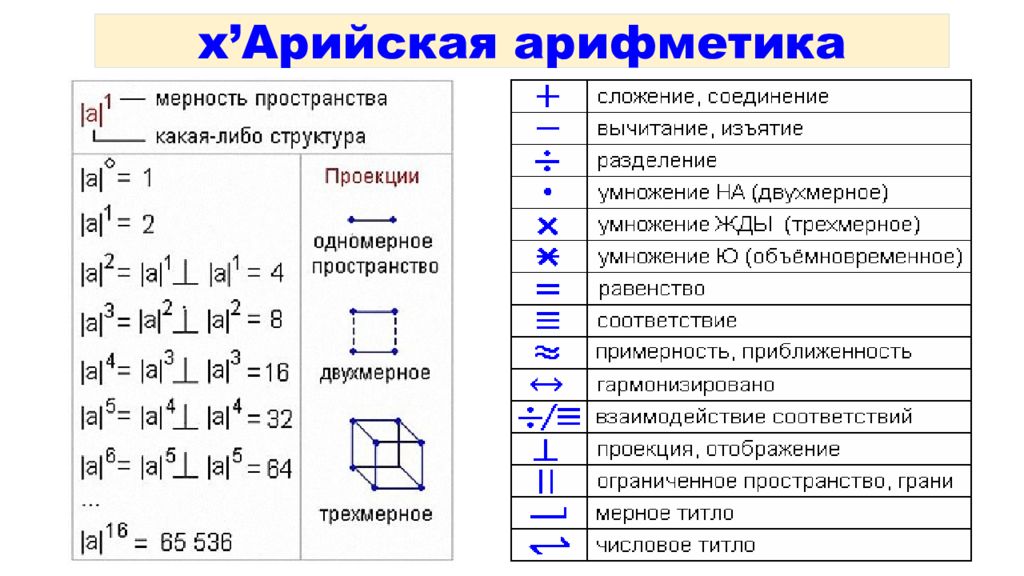
Образная математика (как и х ’ Арийская ) – это предмет, который учит считать образами, в отличие от современной математики, которая считает абстрактные цифры, т.е. непонятно что. Цифры не несут в себе никаких образов, поэтому возникает путаница, дети трудно воспринимают эту арифметику… Цифра - это знак, который служит для составления чисел. Цифр – 10. А Число - это последовательность цифр, используемое для количественной характеристики, сравнения и нумерации объектов. Знаки х ’ Арийского определения (знаки вычисления ): «+» сложение, соединение, «—» вычитание, изъятие. Вычитать – значит что-то убрать, поэтому иногда говорят «вычисление», т.е. вычислить, что убрать. « ÷ » разделение.
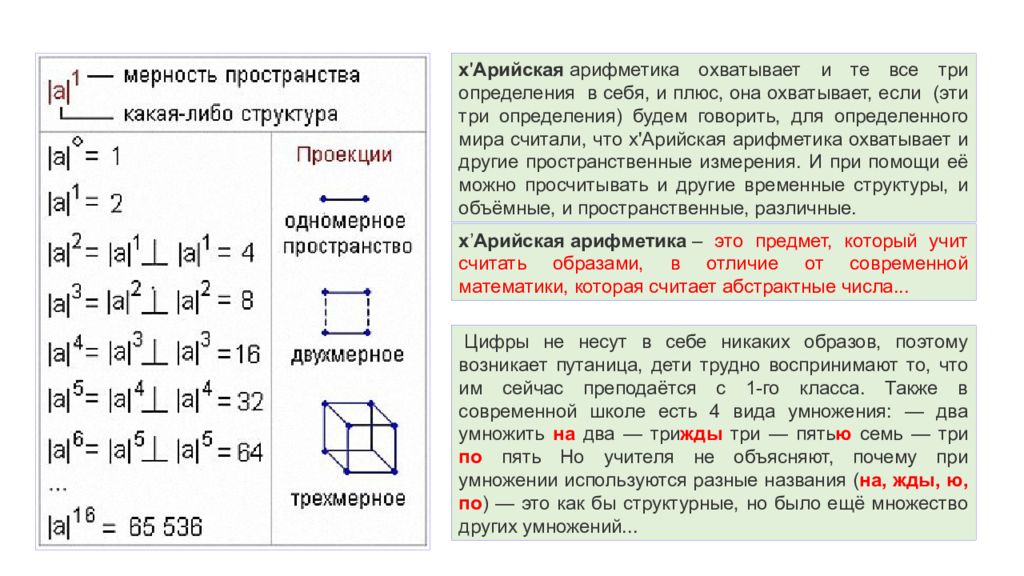
Структура у нас единая, изначальная, т.е. АЗ овая, поэтому будем обозначать её |а| — « азъ », она будет передавать любую структуру и отображать любую проекцию. Теперь представьте: есть Миры-пространства, Миры с дробными пространствами, есть что-то внепространственное, но это внепространственное всё равно имеет какую-то характеристику. Как мы единое передадим вне всякого пространства? А это и будет та самая изначальная точка, которую учёные называют точка сингулярности (в теории «Большого взрыва». В Общей теории относительности А. Эйнштейна.). Нулевое пространство « Некогда, вернее тогда, когда ещё не было времён, не было Миров и Реальностей, нами людьми воспринимаемых, был, не воплощаясь, один только Великий Ра-М-Ха. Он проявился в Новую Действительность и от восприятия Новой Безкрайней Безконечности озарился Великим Светом Радости» — Книга Света, харатья 1, Начало. Веды говорят о том, что было такое состояние, когда не было времён и пространств, т.е. было что-то безвременное и безпространственное. Но заметьте, Ра-М-Ха проявился в Новую Действительность, значит где-то была Старая Действительность. Он наткнулся на Новую Действительность и от него пошёл Свет, в котором появились Вселенные. Здесь говорится о той самой точке, которую учёные называют точка сингулярности, когда Вселенная (или чтобы это ни было) была в единой внепространственной структуре. Только учёные так и не знают, кто поднёс «спичку», чтобы это всё рвануло, ведь у них в основе — теория большого взрыва. А по Ведам, это просто не воплощаясь Ра-М-Ха проявился, и от него Свет Радости (поток Инглии ) наполнил жизнью, и жизнь появилась. |а|° – это нулевое пространство, т.е. как бы его отсутствие. И в этом нулевом пространстве Великий Ра-М-Ха был един, не воплощаясь. Поэтому: |а|° = 1.
Одномерное пространство |а|1 – одномерное пространство. Когда пошёл Свет (который мы называем Инглия ), появилась первая пространственная характеристика, которую начал заполнять Свет. И как только Свет начал наполнять, в этот момент: «В Новой Действительности появилось сверхвеликое абсолютное Нечто». А так как Нечто не было тем, чем являлся Ра-М-Ха, значит оно стало точкой противоположности. А если есть что-то одно и ему противоположное, это равно двум, как бы светлое и тёмное. Поэтому: |а|1 = 2. ПОДПРАВИЛО: любая фигура, объект или структура одномерного пространства будет иметь 2 опорные точки (если образно, то эти точки: Инглия и Нечто). ПРИМЕР одномерного пространства. Если на листе бумаги нарисовать любой рисунок, многоугольник или даже точку, и посмотреть на лист сбоку, получится одна линия, а по бокам две опорные точки, т.е. два начала между которыми они упираются. Поэтому проекция изначальной точки в одномерном пространстве — линия (отрезок). Вспомните, когда в школе рисовали оси координат, всегда изображали где-то минус безконечность, где-то плюс безконечность. Вот этот плюс безконечность – это положительное, светлое, а минус безконечность – как бы мрачное, уходящее во мрак. Двухмерное пространство Чтобы получить структурную характеристику какого-то отрезка в двухмерном пространстве, мы должны провести проекцию к длине отрезка на длину данного отрезка. Т.е. спроецировать отрезок на его длину. Получим квадрат, у которого 4 опорные точки.
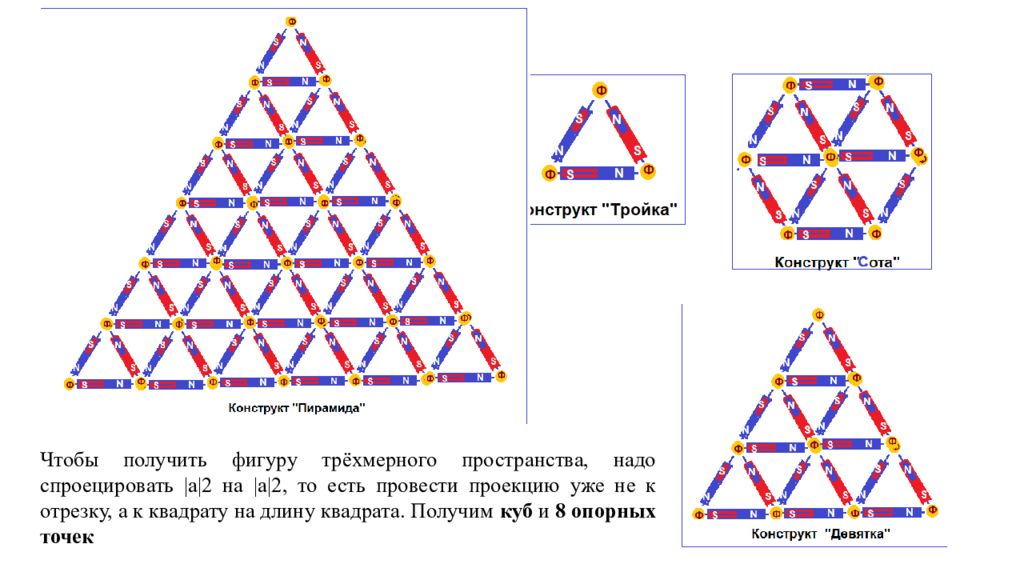
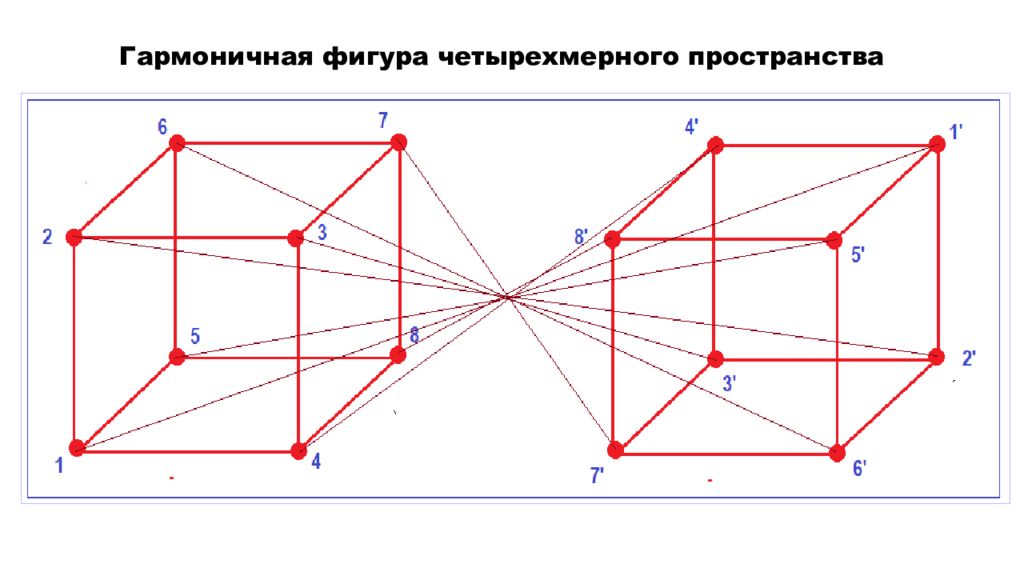
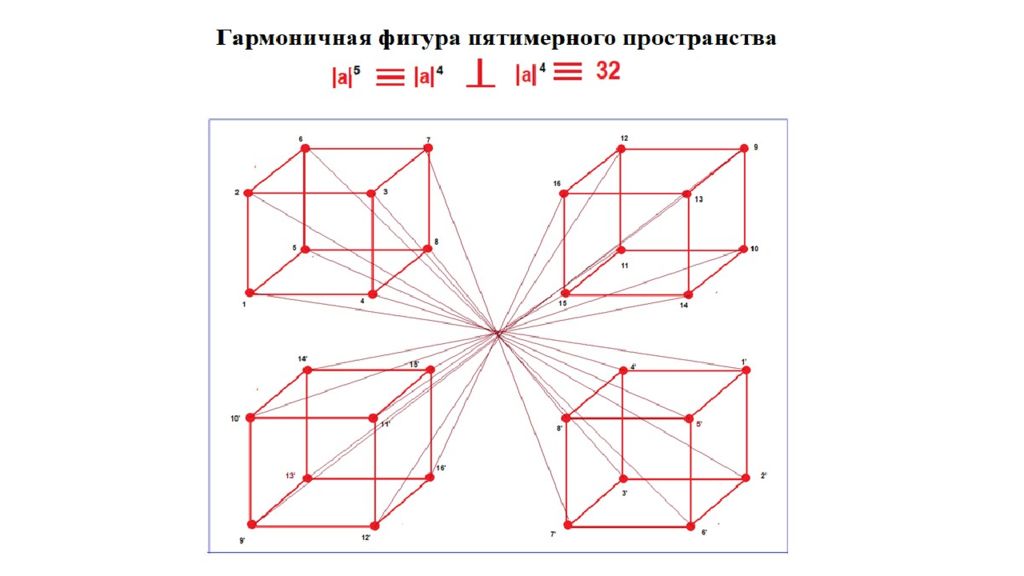
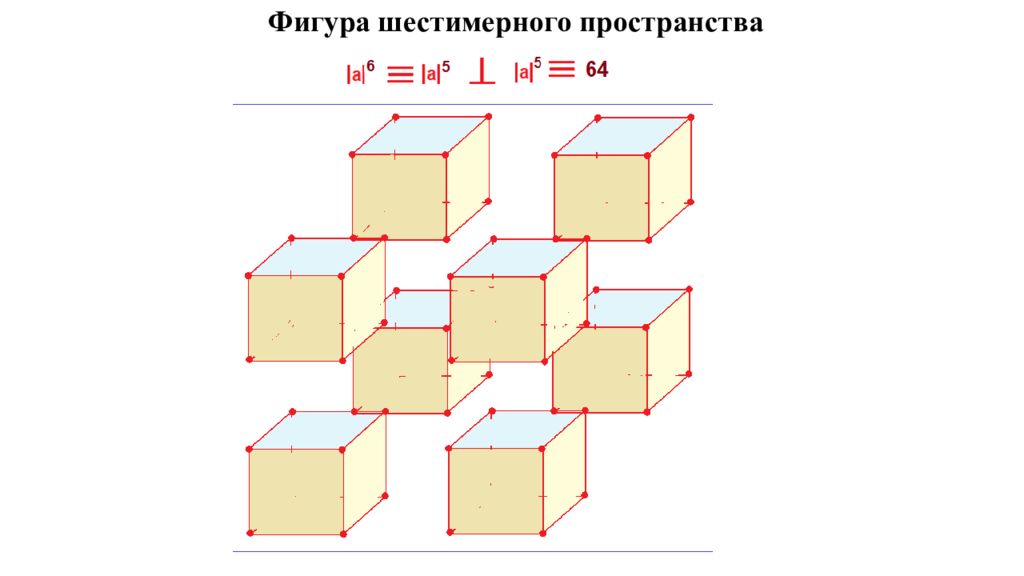
Трёхмерное пространство Чтобы получить фигуру трёхмерного пространства, надо спроецировать |а|2 на |а|2, то есть провести проекцию уже не к отрезку, а к квадрату на длину квадрата. Получим куб и 8 опорных точек. Четырёхмерное пространство Чтобы получить четырёхмерную фигуру, надо провести проекцию |а|3 на длину |а|3, т.е. спроецировать куб на длину куба. Таким образом, характеристику выводим в сторону и получается куб в кубе и 16 опорных точек. Т.е. увеличилась плотность фигур, но и увеличилось количество опорных точек в пространстве. И так далее, в пятимерном пространстве будет 32 опорные точки, в шестимерном 64, в семимерном 128… в шестнадцатимерном пространстве 65 536 опорных точек. Шестнадцатимерное пространство – это следующее за нашим 4-хмерным гармоничное пространство. Если у нас здесь раскрыто 16 каналов (см. энергоновая система крови ), то там будет раскрыто 256 каналов. Дважды два = 4? И заметьте, мы говорим о трёхмерности. Куб имеет 8 опорных точек, поэтому, когда умножаем ЖДЫ ( два куба в пространстве ), получаем 16. Поэтому когда вам в школе сказали, что 2+2 = 4, дважды два = 4, 2 во второй степени = 4 — вас два раза из трёх обманули. 2+2=4; 2х2 = 16 (дважды два = 16); 2 во второй степени = 3,9999… и никогда не будет равно 4, потому что мерность нашего пространства не равна четырём, и не равна трём.
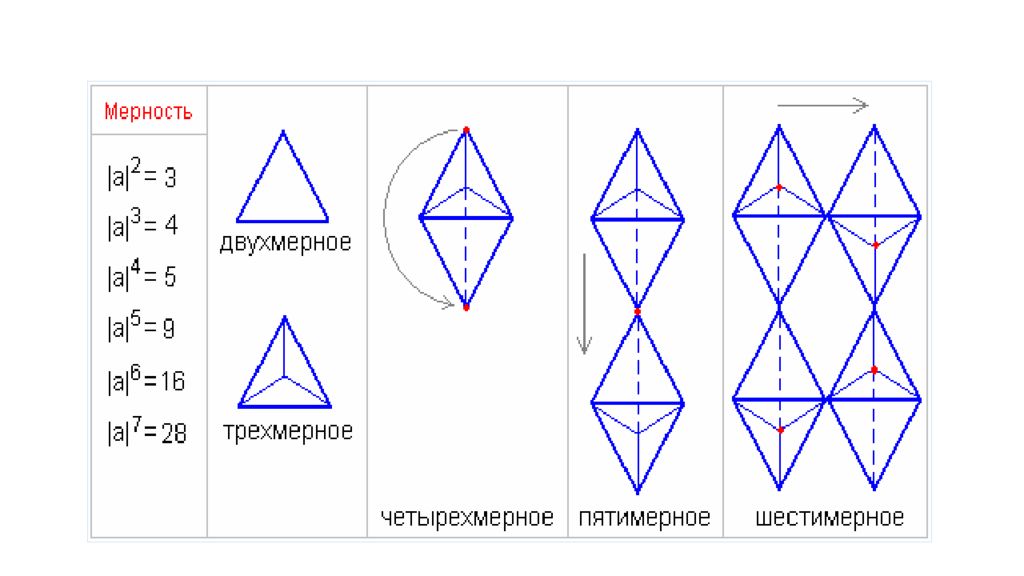
Определение мерности при использовании чётко структурных изображений Мы уже разобрали гармоничные фигуры (см. структурные проекции ), теперь также займёмся проекцией, только в отображении к чёткой структуре, где |а| двухмерное = 3, т.е. три опорные точки. Чтобы вам было проще это воспринять, изобразим на двухмерности чёткую структуру — треугольник. Трёхмерность. Чтобы получить трёхмерную структуру, необходимо спроецировать двухмерную по всем сторонам. Получится 4 опорные точки. Трёхмерность. Чтобы получить трёхмерную структуру, необходимо спроецировать двухмерную по всем сторонам. Получится 4 опорные точки. Четырёхмерность. Четвёртая считается как бы во времени, поэтому для получения четырёхмерной фигуры, мы должны спроецировать структурно (два « тетрапака » соединённые между собой дном). Получается 5 опорных точек. Пятимерность. Проецируем четырёхмерную в пространстве, через одну общую точку. Получается 9 опорных точек. Шестимерность. Для получения шестимерной структуры, проецируем предыдущую через общие точки. Получается 16 опорных точек. Семимерность. Чтобы получить семимерную структуру, необходимо на шестимерную наложить точно такую же, через общие точки (выделены красным цветом, они на нас выходят). Получится 28 опорных точек.
Чтобы получить фигуру трёхмерного пространства, надо спроецировать |а|2 на |а|2, то есть провести проекцию уже не к отрезку, а к квадрату на длину квадрата. Получим куб и 8 опорных точек
х ' Арийская арифметика охватывает и те все три определения в себя, и плюс, она охватывает, если (эти три определения) будем говорить, для определенного мира считали, что х'Арийская арифметика охватывает и другие пространственные измерения. И при помощи её можно просчитывать и другие временные структуры, и объёмные, и пространственные, различные. х ’ Арийская арифметика – это предмет, который учит считать образами, в отличие от современной математики, которая считает абстрактные числа... Цифры не несут в себе никаких образов, поэтому возникает путаница, дети трудно воспринимают то, что им сейчас преподаётся с 1-го класса. Также в современной школе есть 4 вида умножения: — два умножить на два — три жды три — пять ю семь — три по пять Но учителя не объясняют, почему при умножении используются разные названия ( на, жды, ю, по ) — это как бы структурные, но было ещё множество других умножений...
х ’ Арийская арифметика
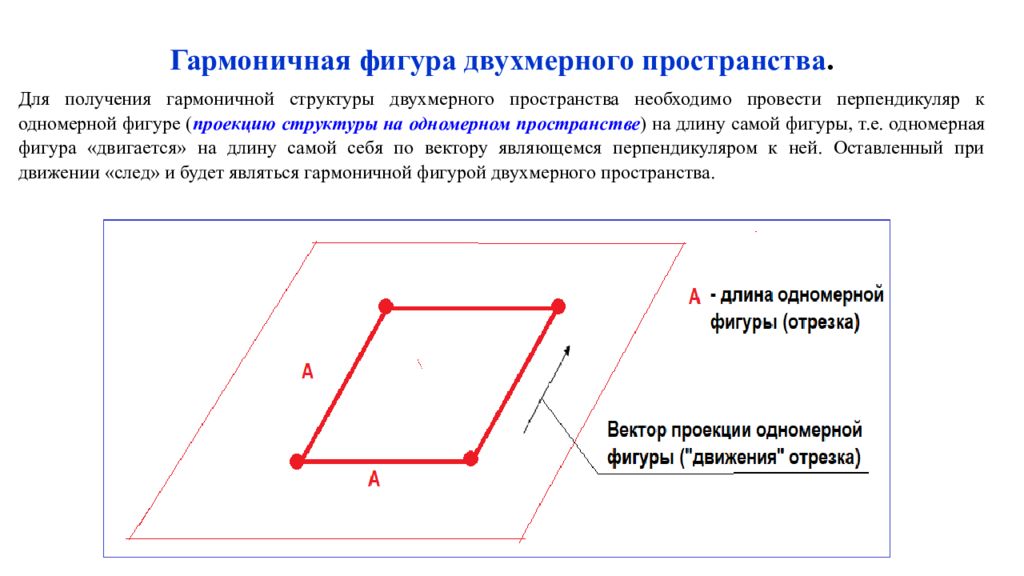
Гармоничная фигура двухмерного пространства. Для получения гармоничной структуры двухмерного пространства необходимо провести перпендикуляр к одномерной фигуре ( проекцию структуры на одномерном пространстве ) на длину самой фигуры, т.е. одномерная фигура «двигается» на длину самой себя по вектору являющемся перпендикуляром к ней. Оставленный при движении «след» и будет являться гармоничной фигурой двухмерного пространства.
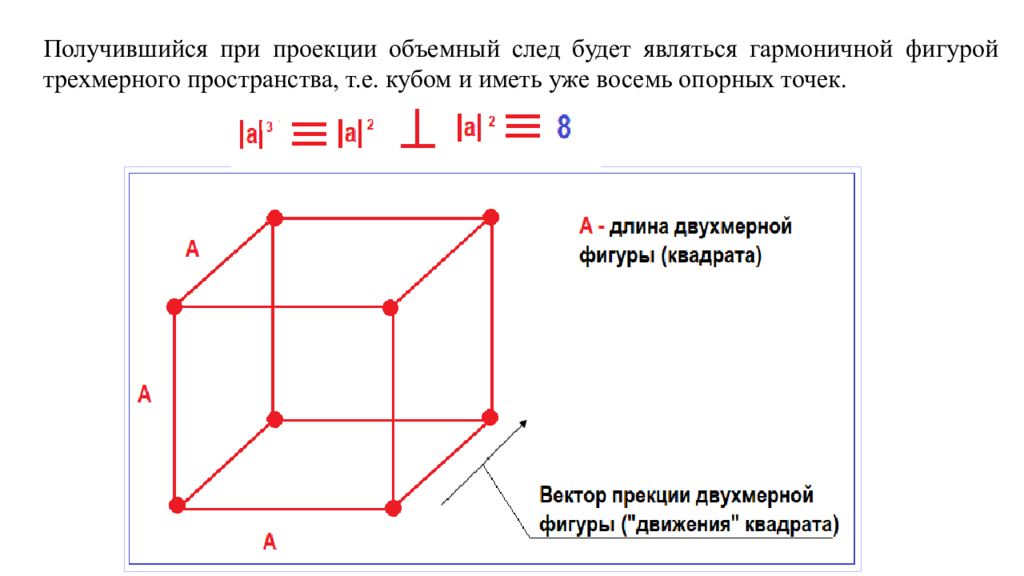
Получившийся при проекции объемный след будет являться гармоничной фигурой трехмерного пространства, т.е. кубом и иметь уже восемь опорных точек.
Гармоничная фигура четырехмерного пространства
Фигура шестимерного пространства
Таблица соответствий гармоничных фигур разномерных пространств с количеством их опорных точек.
