Алгебра логики Информатика 9 класс
Логическое отрицание - ИНВЕРСИЯ Образуется из высказывания с помощью добавления частицы «НЕ» к сказуемому или использования оборота речи «НЕВЕРНО, ЧТО...» Обозначение : Ā, ¬А, не А, not А Таблица истинности: Примеры инверсии: А= «Неверно, что у меня есть приставка Dendy » В= «Я не знаю китайского языка» Инверсия высказывания истинная, когда высказывание ложно, и ложна, когда высказывание истинно.
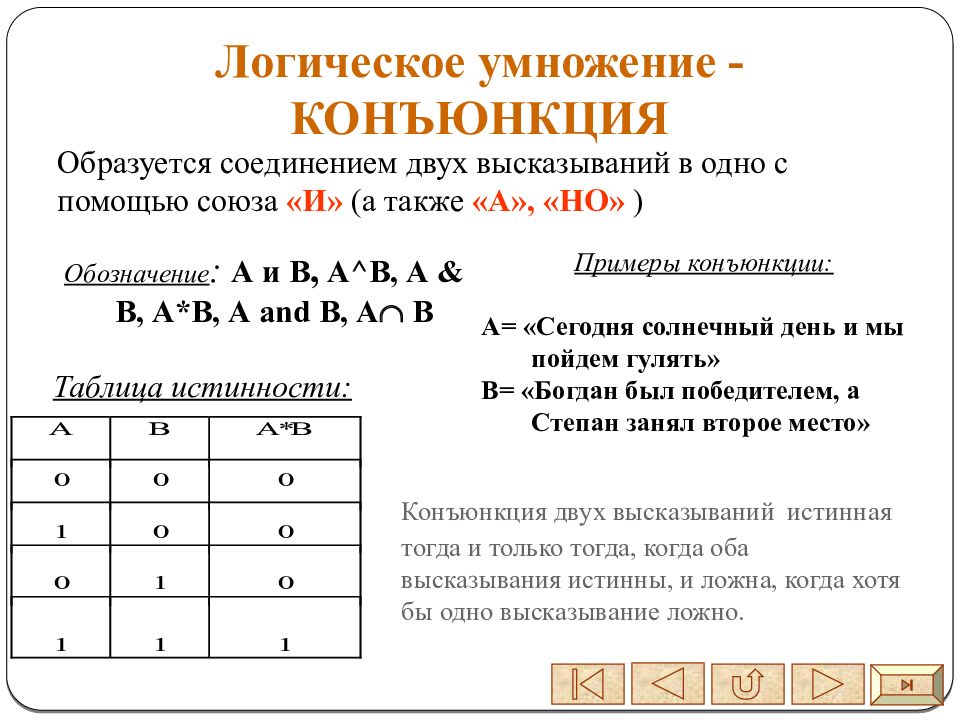
Логическое умножение - КОНЪЮНКЦИЯ Образуется соединением двух высказываний в одно с помощью союза «И» (а также «А», «НО» ) Обозначение : А и В, А^В, А & В, А*В, А and B, А B Таблица истинности: Примеры конъюнкции: А= «Сегодня солнечный день и мы пойдем гулять» В= «Богдан был победителем, а Степан занял второе место» Конъюнкция двух высказываний истинная тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно.
Логическое сложение - ДИЗЪЮНКЦИЯ Образуется соединением двух высказываний в одно с помощью союза «ИЛИ» (нестрогая), «ЛИБО» (строгая) Обозначение : А или В, АV В, А | В, А+В, А or B, А B; AB, A xor B Таблица истинности: Примеры дизъюнкции: А= «Снег пойдет ночью или утром» В= «Он приедет сегодня либо завтра» Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно высказывание истинно.
Логическое следование - ИМПЛИКАЦИЯ Образуется соединением двух высказываний в одно с помощью оборота речи «ЕСЛИ …, ТО...» Обозначение : А В, А В Таблица истинности: Примеры импликации: А= «Если число делится на 9, то оно делится на 3» В= «Если на улице дождь, то асфальт мокрый» Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное.
Логическое равенство - ЭКВИВАЛЕНТНОСТЬ Образуется соединением двух высказываний в одно с помощью оборота речи «… ТОГДА И ТОЛЬКО ТОГДА, КОГДА...» Обозначение : А В, А В, А=В, А В, А~В Таблица истинности: Примеры эквивалентности: А= «Число кратно 3 тогда и только тогда, когда сумма цифр числа делится нацело на 3» В= «Угол называется прямым тогда и только тогда, когда он равен 90°» Эквивалентность двух высказываний истинна тогда и только тогда, когда оба высказывания истинны или оба ложны.
Инверсия Конъюнкция Дизъюнкция Импликация Эквивалентность не А; неверно, что А и А, и В; как А, так и В; А вместе с В; А несмотря на В; А, в то время как В; А и В А или В; А либо В; либо А, либо В; строго А или В если А, то В; В, если А; В необходимо для А; А достаточно для В; А только тогда, когда В; В тогда, когда А; все А есть В А эквивалентно В; А необходимо и достаточно для В; А тогда и только тогда, когда В
инверсия конъюнкция дизъюнкция импликация эквивалентность Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
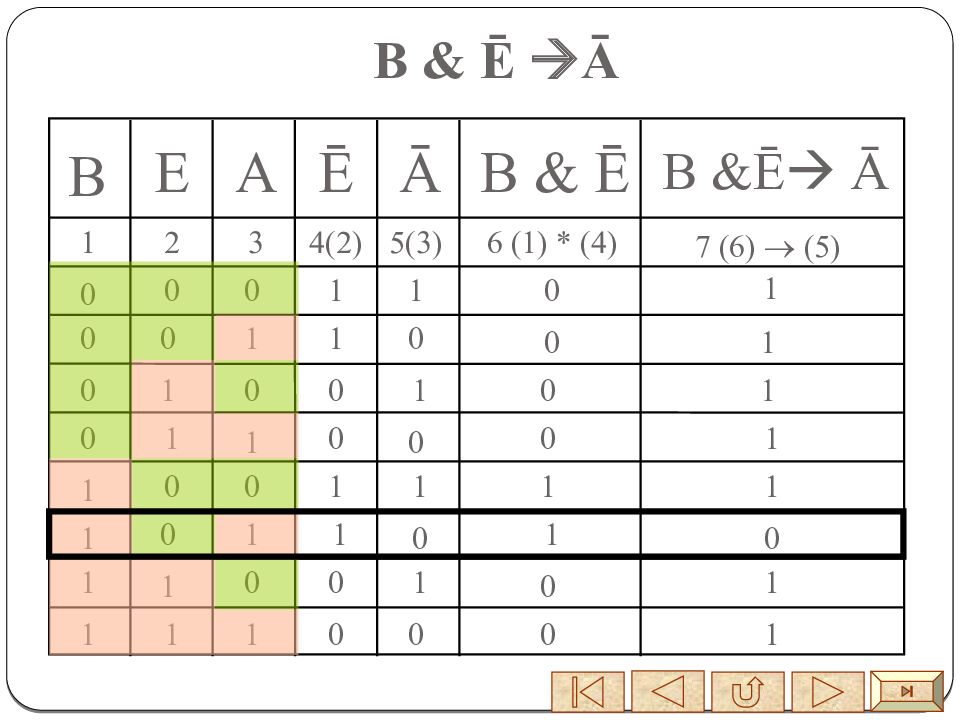
Определяем количество переменных в логической функции – N. N = 3 Определить количество строк ( Q ) в таблице: Q = 2 3 = 8 Определяем количество логических операций (К) и последовательность их выполнения. K = 3 Определяем количество столбцов: N + K = 6 Заполняем исходные данные таблицы: разделить колонку значений первой переменной пополам и заполнить верхнюю половину 0, нижнюю половину 1; так делать до тех пор, пока группы 0 и 1 не будут состоять из одного символа. Выполнять логические операции для каждого столбца.
1 3 4(2) 5(3) 6 (1) * (4) 7 (6) (5) 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 1 0 1 1 0 0 0 1 1 0 0 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 0 0 1 1 В Е А Ē Ā В & Ē В & Ē Ā 2 В & Ē Ā
