Первый слайд презентации: Аналитическая геометрия в пространстве
Плоскость и прямая в пространстве
Слайд 2: Плоскость
Основные уравнения плоскости 1. Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору 2. Общее уравнение плоскости - вектор нормали 3. Уравнение плоскости « в отрезках»
Слайд 3: Уравнения плоскости
4. Уравнение плоскости, проходящей через три заданные точки, и Условие компланарности векторов
Слайд 4: Составление уравнений плоскости
1. Составить уравнение плоскости, проходящей через точку перпендикулярно вектору Исходное уравнение: Подставляем координаты точки и вектора Раскрываем скобки Приводим подобные Получили общее уравнение плоскости.
Слайд 5
2. Составить уравнение плоскости, проходящей через три заданные точки В данном случае можно воспользоваться формулой уравнения плоскости, проходящей через три точки: Подставляем в это уравнение координаты точек и раскладываем определитель по элементам первой строки
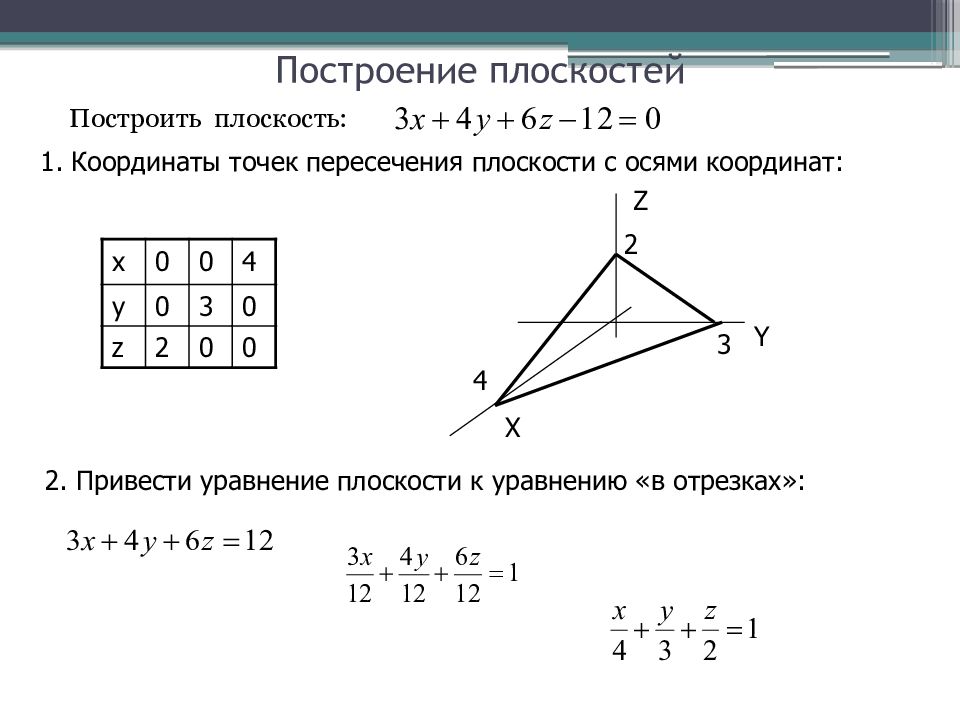
Слайд 6: Построение плоскостей
Построить плоскость: 1. Координаты точек пересечения плоскости с осями координат: x 0 0 4 y 0 3 0 z 2 0 0 Z Y X 2 3 4 2. Привести уравнение плоскости к уравнению «в отрезках»:
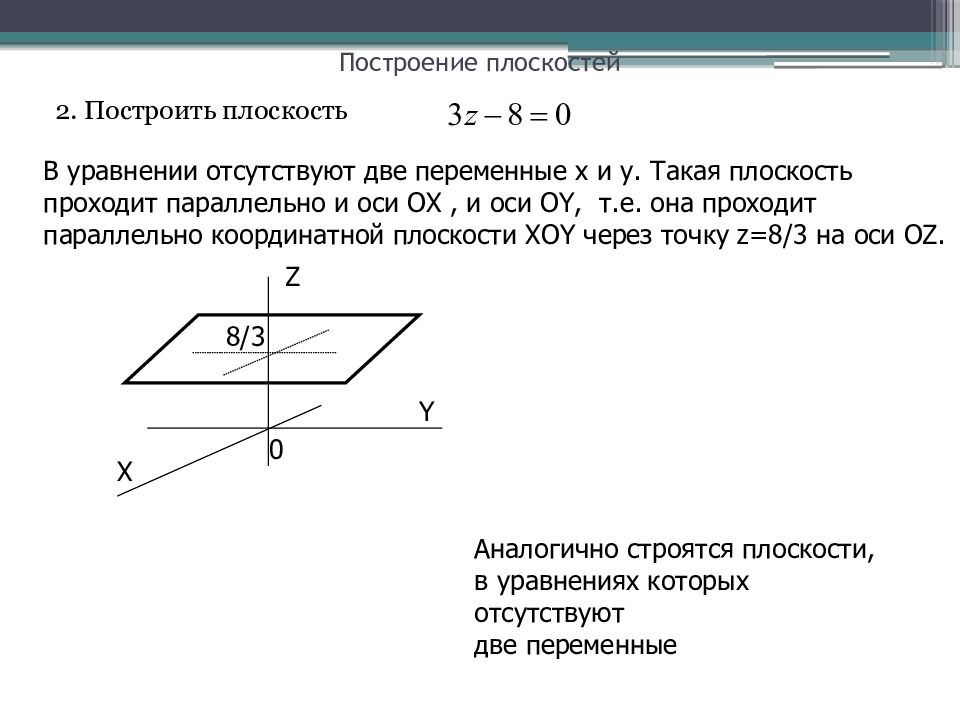
Слайд 7: Построение плоскостей
2. Построить плоскость В уравнении отсутствуют две переменные x и y. Такая плоскость проходит параллельно и оси OX, и оси OY, т.е. она проходит параллельно координатной плоскости XOY через точку z= 8/3 на оси OZ. Z Y X 8/3 0 Аналогично строятся плоскости, в уравнениях которых отсутствуют две переменные
Слайд 8
Если в уравнении плоскости отсутствует одна переменная, то плоскость проходит параллельно той оси координат, переменной которой нет в уравнении. Если в уравнении плоскости отсутствует свободный коэффициент, то плоскость проходит через начало координат. Если в уравнении плоскости отсутствуют две переменные, то плоскость проходит параллельно координатной плоскости, переменных которой нет в уравнении. Уравнения координатных плоскостей - уравнение плоскости YOZ - уравнение плоскости XOZ - уравнение плоскости XOY
Слайд 9: Взаимное расположение плоскостей
1. Условие параллельности плоскостей 2. Условие перпендикулярности плоскостей 3. Косинус угла между плоскостями Угол между плоскостями – это угол между векторами нормалей этих плоскостей
Слайд 10: Расстояние от точки до плоскости
Расстояние от точки до плоскости находится по формуле Расстояние – это длина перпендикуляра, опущенного из точки на плоскость
Слайд 11
Найти расстояние от точки до плоскости Используем формулу расстояния от точки до плоскости
Слайд 12: Прямая в пространстве. Основные уравнения
1. Уравнение прямой, проходящей через заданную точку параллельно заданному вектору - канонические уравнения - направляющий вектор 2. Параметрические уравнения 3. Уравнение прямой, проходящей через две заданные точки и
Слайд 13: Прямая в пространстве. Основные уравнения
4. Общее уравнение прямой в пространстве Направляющий вектор
Слайд 14: Взаимное расположение прямых в пространстве
1. Нахождение угла между прямыми. Прямые в пространстве заданы каноническими уравнениями, поэтому угол между прямыми – это угол между направляющими векторами 2. Проверка условий параллельности и перпендикулярности прямых Условие параллельности прямых Условие перпендикулярности прямых
Слайд 15: Расстояние от точки до прямой в пространстве
Задача о нахождении расстояния от точки до прямой На векторах И строим параллелограмм. Высота этого параллелограмма – искомое расстояние. Высоту находим как отношение площади параллелограмма к длине основания. Площадь параллелограмма – это модуль векторного произведения векторов, а длина основания – это длина вектора
Слайд 16
Найти расстояние от точки до прямой d Искомое расстояние – это высота параллелограмма, построенного на векторах и Площадь параллелограмма находим, используя векторное произведение Длина основания – это длина вектора Расстояние от точки до прямой
Слайд 17: Взаимное расположение прямой и плоскости в пространстве
1. Условие параллельности прямой и плоскости 2. Условие перпендикулярности прямой и плоскости
Слайд 18: Взаимное расположение прямой и плоскости в пространстве
3. Нахождение угла между прямой и плоскостью Углом между прямой и плоскостью- угол между этой прямой и ее ортогональной проекцией на эту плоскость Из уравнений прямой и плоскости известны направляющий вектор прямой и вектор нормали плоскости. Угол между этими векторами - Так как в сумме углы дают 90 градусов, а значит Поэтому при нахождении угла между прямой и плоскостью находят не косинус, а синус угла. Так как синус угла между прямой и плоскостью может быть только положительным, то:
Слайд 19: Решение типовых задач
1. Составить уравнение плоскости, проходящей через точку параллельно двум векторам и Используем уравнение Координаты точки нам известны. Необходимо найти координаты вектора нормали. Из рисунка видно, что в качестве вектора нормали можно взять вектор, являющийся векторным произведением данных в условии задачи векторов, так как такой вектор перпендикулярен каждому из данных векторов, а значит перпендикулярен и плоскости. Итак, Подставляем все данные в уравнение плоскости
Слайд 20
2. Составить уравнение плоскости, проходящей через точку перпендикулярно двум плоскостям Для составления уравнения плоскости есть точка. Вектором нормали может являться вектор, равный векторному произведению векторов нормалей данных плоскостей. Основное уравнение: Остается только подставить все данные в уравнение.
Слайд 21
3. Составить уравнение плоскости, проходящей через точку перпендикулярно прямой Из рисунка видно, что в качестве вектора нормали плоскости можно взять направляющий вектор прямой Таким образом, для составления уравнения плоскости есть все данные: координаты точки и вектора нормали Основное уравнение плоскости
Слайд 22
4. Составить уравнение плоскости, проходящей через точку и отсекающую на осях координат одинаковые отрезки Для решение задачи используем уравнение плоскости «в отрезках» Отрезки на осях одинаковые, поэтому или Для нахождения подставляем в это уравнение координаты точки Итак, уравнение плоскости:
Слайд 23
5. Составить уравнение прямой, проходящей через точку параллельно оси OY. Канонические уравнения прямой 6. Составить канонические уравнения прямой, проходящей через две точки В качестве направляющего вектора можно использовать вектор, соединяющий эти точки. Уравнения прямой: В качестве направляющего вектора можно использовать любой вектор, параллельный оси OY. Самый простой вектор – это единичный вектор оси OY и ! Использовать можно координаты любой точки
Последний слайд презентации: Аналитическая геометрия в пространстве
7. Составить уравнение прямой, проходящей через точку перпендикулярно плоскости Из рисунка видно, что в качестве направляющего вектора прямой можно взять вектор нормали плоскости Таким образом, для составления уравнения прямой есть все данные: координаты точки и направляющего вектора Канонические уравнения прямой