Первый слайд презентации: Диаметр, радиус и центр графа
Старший преподаватель к афедры теоретической кибернетики Хадиев Р.М. КАЗАНСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
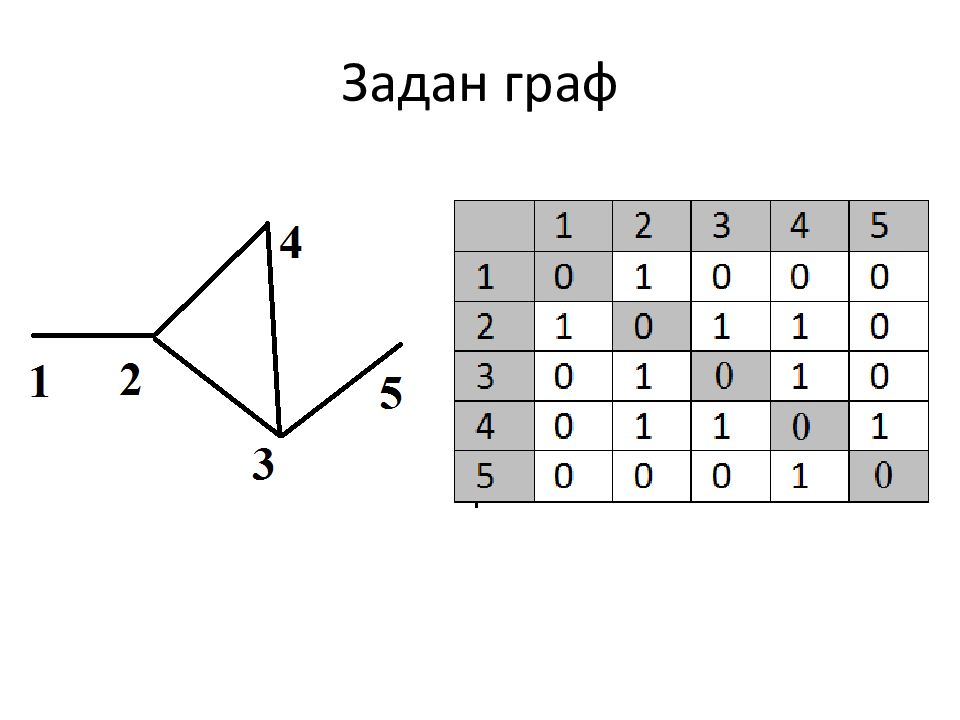
Слайд 3: Ввод данных
int main() { int G[100][100], // граф транспортной сети R[100][100], // минимальные расстояния // между вершинами I,j,n, // n – число вершин cin >> n ; for ( i =1; i <=n; i ++) for (j=1; j<=n; j++) cin >> G[ i ][j];
Слайд 4: O пределение длины кратчайш их путей
int r[100]={0}, // 0 – расстояние не определено ob[100], // обработанные вершины For ( n_p =1; n_p <n; n_p ++) { Int a =1, // вершина из ob, которая обрабатывается p =2 ; // пустое место для записи новых вершин r[ n_p ]=1; // кратчайший путь в n_p – 1 ob[1]= n_p ; // while a<p do { for ( i =0; i <n; i ++ ) // ищем связанные с ob[a] if (G[ i ][ob[a]]==1 & r[ i ]==0) { //необработанные вершины r[ i ]=r[ob[a]]+1; ob[++p]=I; } a++; } for( i =1; i <=n; i ++) R( n_p ][ i ]=r[ i ]; }
Диаметр - 3
Слайд 6: Определение диаметра графа
int D=0; For( i =1; i <=n; i ++) For( i =1; i <=n; i ++) D:= max(D,R[ i ][j]); Cout << “ Диаметр графа = “ << D;
Слайд 7: Определение. Радиус связного графа – максимально возможное расстояние между двумя его вершинами. Для решения задачи строим матрицу кратчайших расстояний между вершинами
Диаметр - 3
Слайд 8: Определение радиуса графа
int Rad =0; for( i =1; i <=n; i ++) { int M=0; for( i =1 ; i <=n; i ++) M:= max(M,R[ i ][j]); if ( i ==1) Rad =M; else Rad =min( Rad,M ); } cout << “ Радиус графа = “ << Rad ;
Слайд 9: Определение. Центр графа – вершина, максимальное расстояние от которого до любой другой вершины является наименьшим из всех возможных. Для решения задачи строим матрицу кратчайших расстояний между вершинами
Цен тр - 2,3 или 4