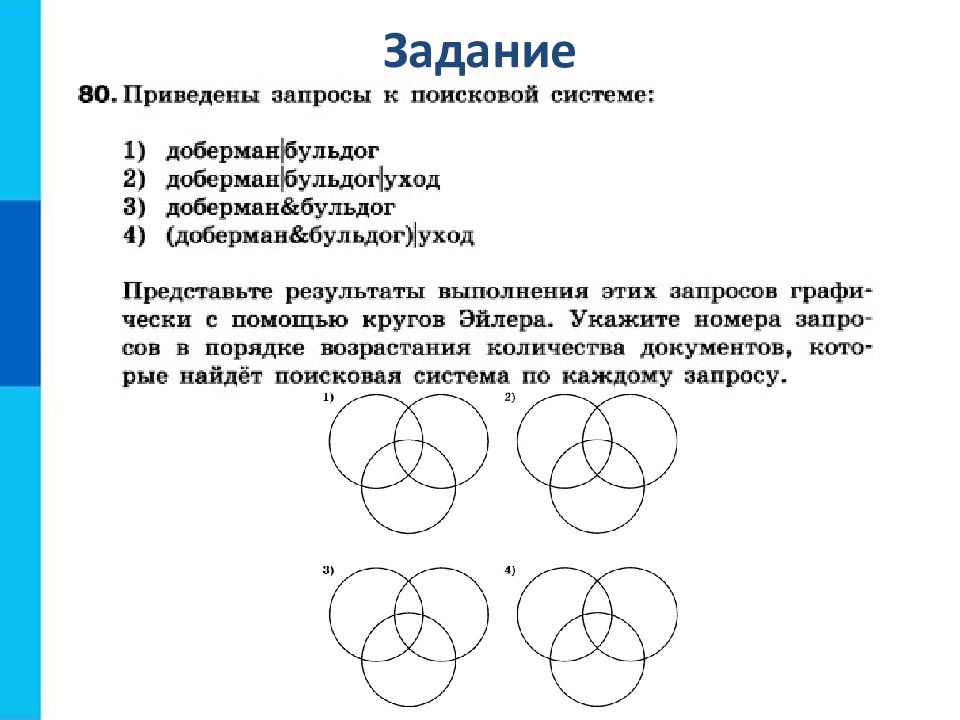
Первый слайд презентации
ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
Слайд 4: Таблицы истинности
Решение логических выражений принято оформлять в виде таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных
Слайд 5: Определение
Таблица истинности – это таблица, с помощью которой устанавливается истинностное значение сложного высказывания при всех значениях входящих в него простых высказываний.
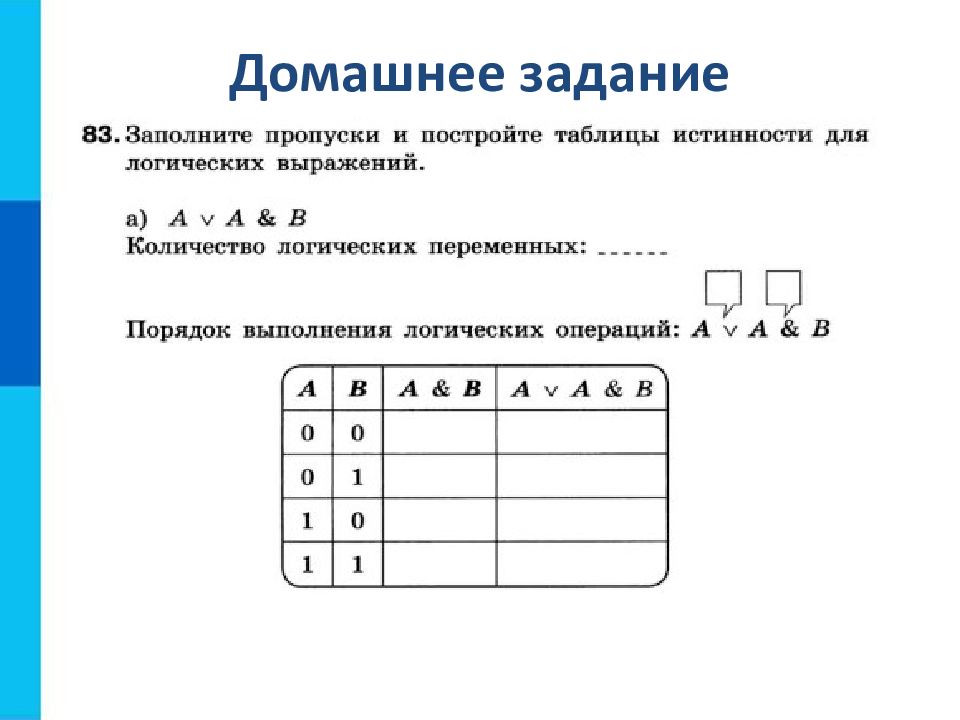
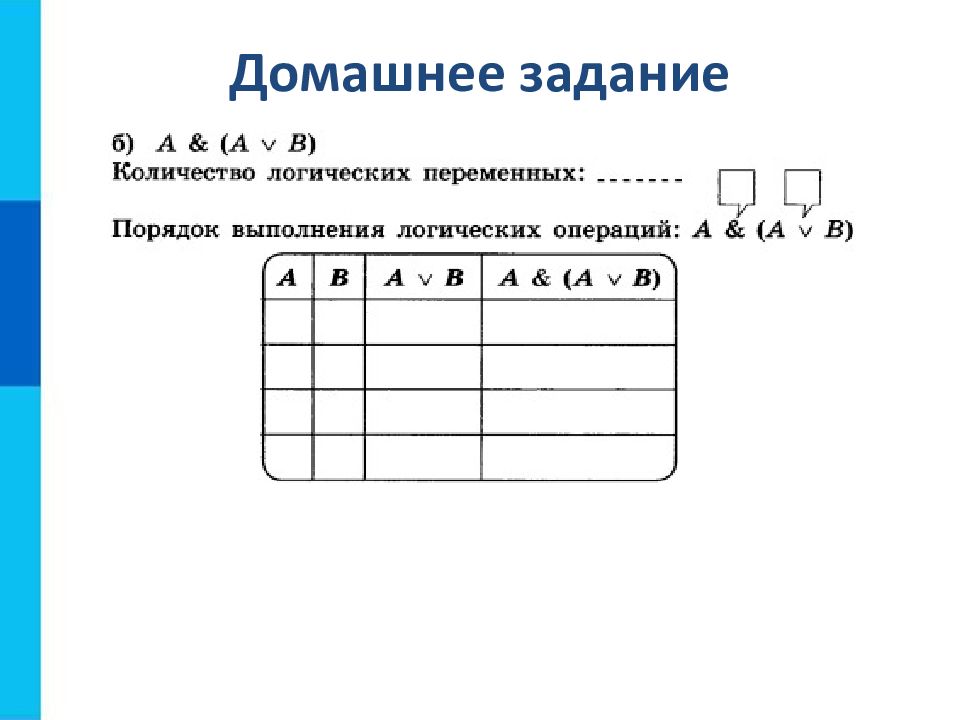
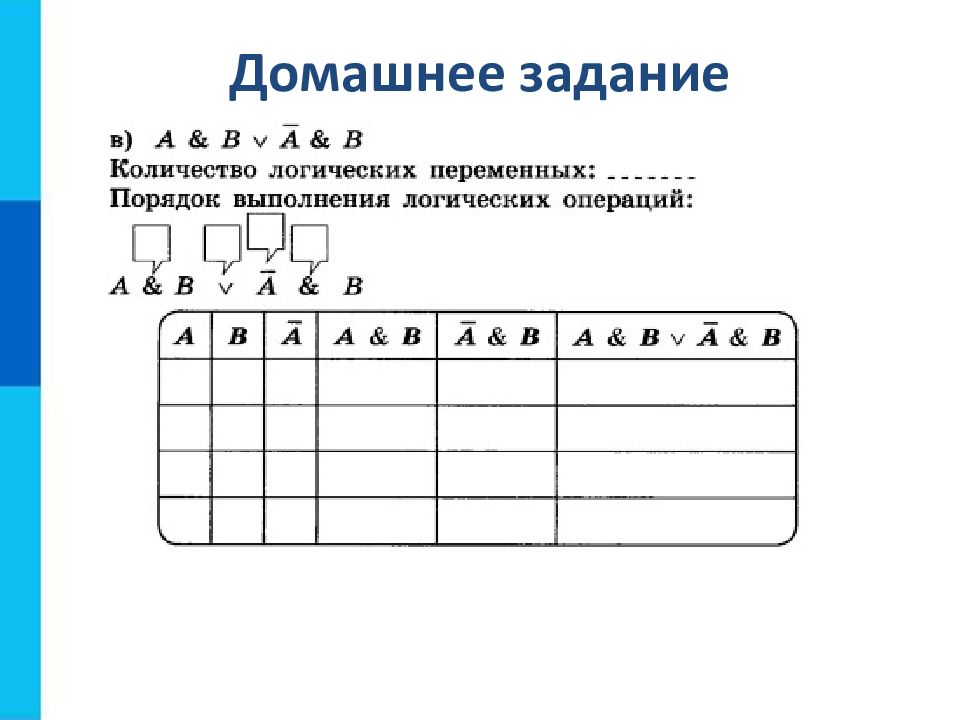
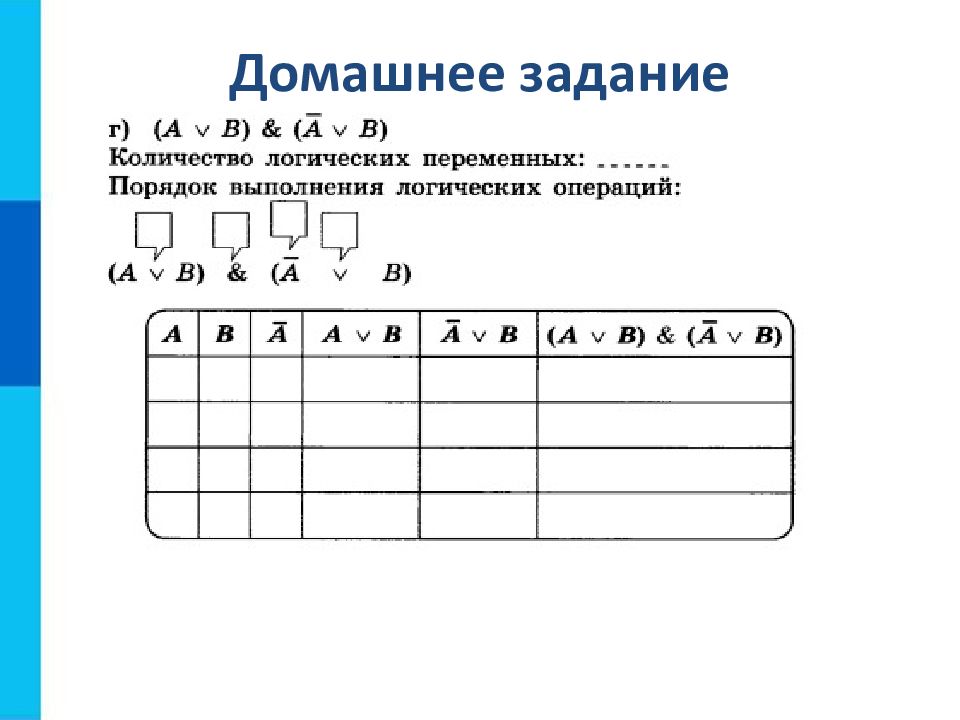
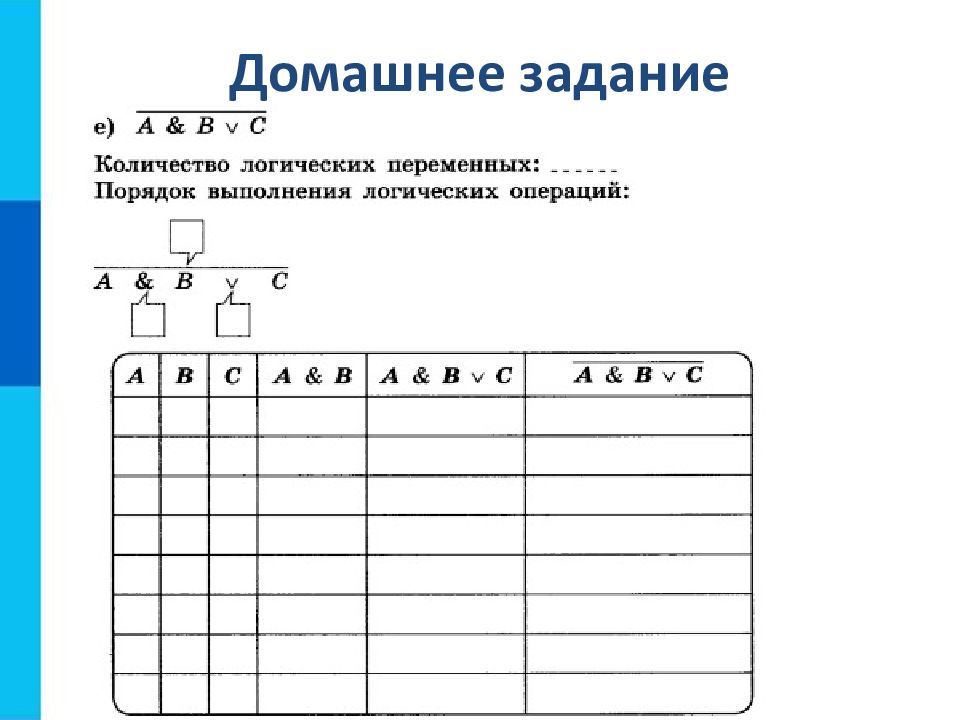
Количество строк = 2 n +1, где n – количество переменных. Количество столбцов = количество переменных + количество логических операций. Установить последовательность выполнения логических операций. Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных. Заполнить таблицу истинности по столбцам.
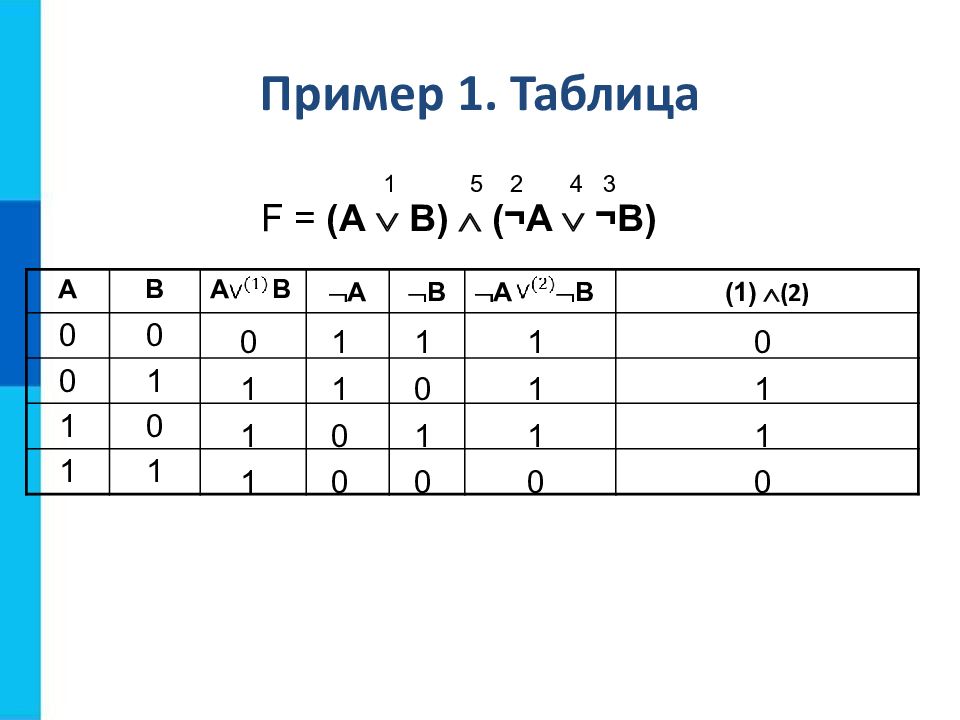
Слайд 7: Пример 1
Построим таблицу истинности для функции F = ( А В ) ( ¬ A ¬ B) Переменных: две (А и В), т.е. N = 2 количество строк : 2 n =2 2 =4. С заголовком: 5 Количество столбцов: 2 переменные + 5 операций ( ,, ¬, и ¬ ). Итого 7 Порядок операций: 1 5 2 4 3 F = ( А В ) ( ¬ A ¬ B)
Слайд 8: Пример 1. Таблица
A B A B А В A B (1) (2) 0 0 0 1 1 0 1 1 0 1 1 1 1 1 0 0 F = ( А В ) (¬A ¬B) 1 0 1 0 1 1 1 0 0 1 1 0 1 5 2 4 3
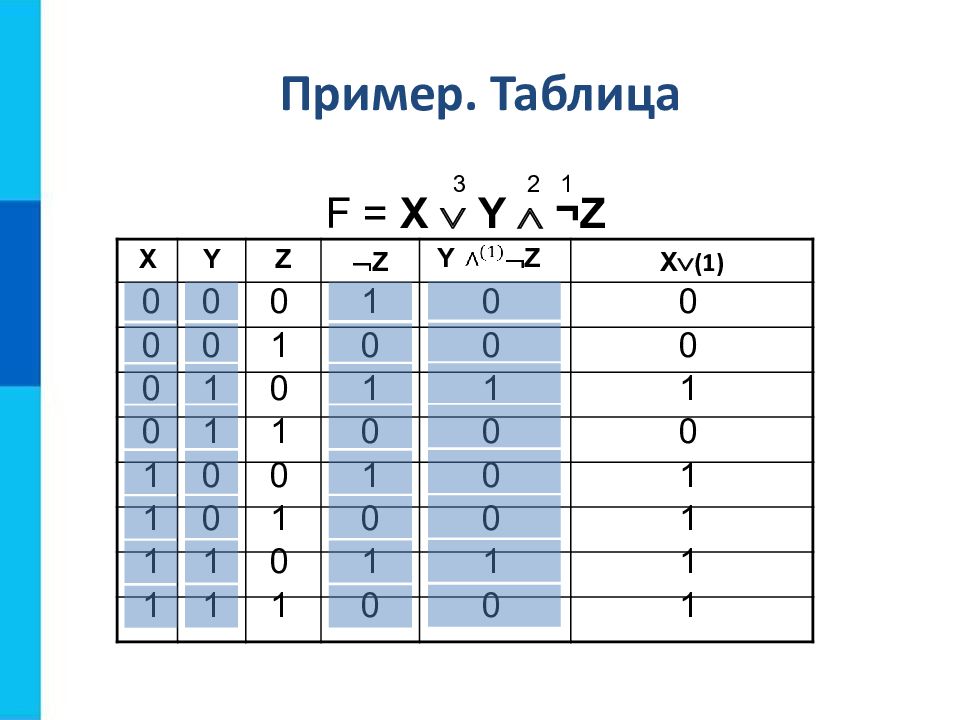
Слайд 9: Пример 2
Построим таблицу истинности для функции F = X Y ¬ Z Переменных: три ( X, Y и Z ), т.е. n = 3 количество строк : 2 n =2 3 =8. С заголовком: 9 Количество столбцов: 3 переменные + 3 операции ( ,, ¬ ). Итого 6 Порядок операций: 3 2 1 F = X Y ¬ Z
Слайд 10: Пример. Таблица
X Y Z Z Y Z X (1) 0 0 0 0 1 1 1 1 F = X Y ¬Z 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 3 2 1
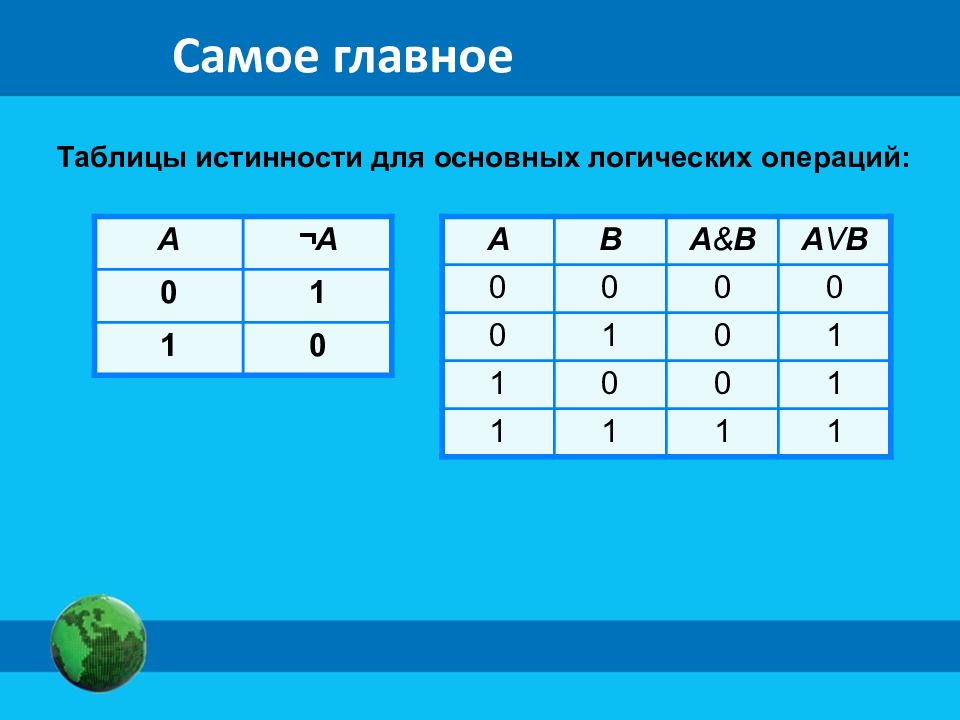
Слайд 11
Таблицы истинности для основных логических операций: А ¬ А 0 1 1 0 A B A & B A V B 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 1 Самое главное