ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
Ключевые слова логические элементы
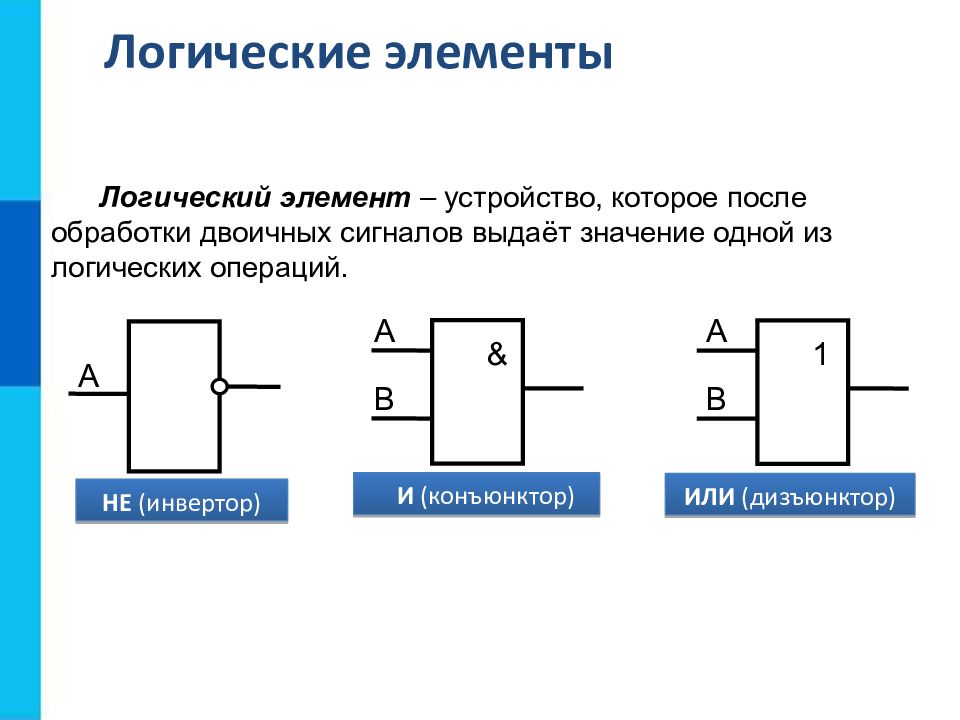
Логический элемент – устройство, которое после обработки двоичных сигналов выдаёт значение одной из логических операций. & А В И ( конъюнктор ) 1 А В ИЛИ ( дизъюнктор ) НЕ (инвертор) А Логические элементы
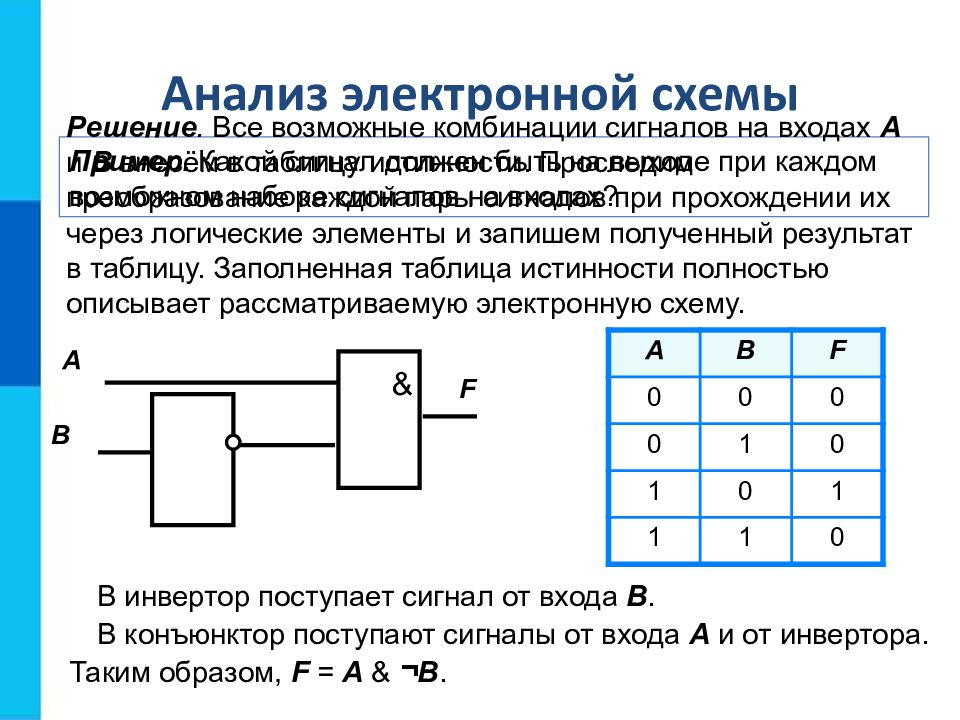
Пример. Какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах? Анализ электронной схемы Решение. Все возможные комбинации сигналов на входах А и В внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную схему. А В & F A B F 0 0 0 0 1 0 1 0 1 1 1 0 В инвертор поступает сигнал от входа В. В конъюнктор поступают сигналы от входа А и от инвертора. Таким образом, F = A & ¬ B.
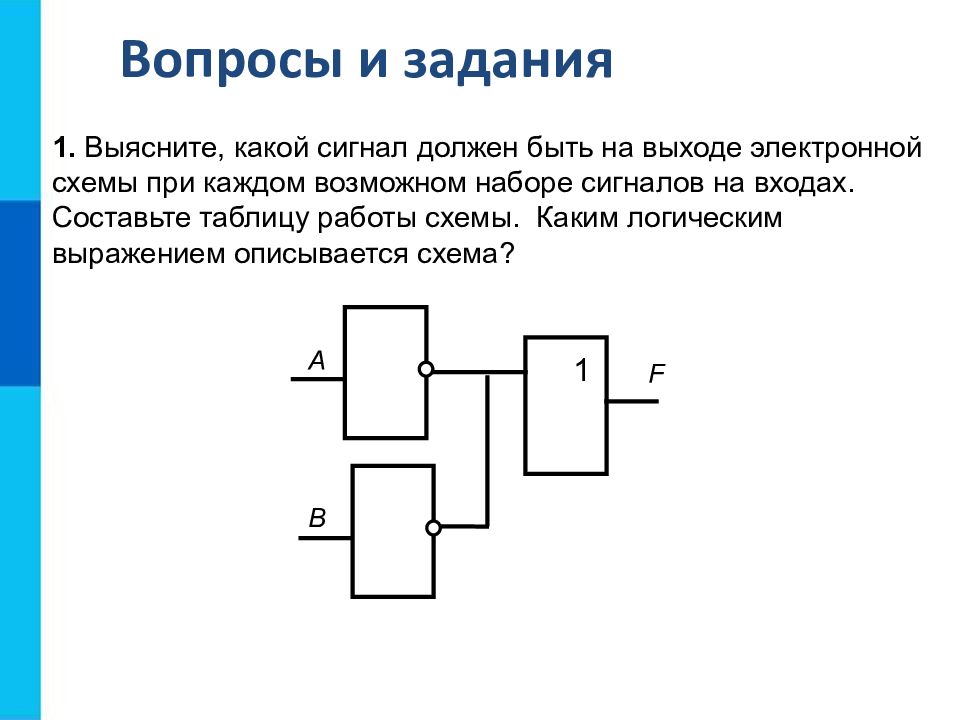
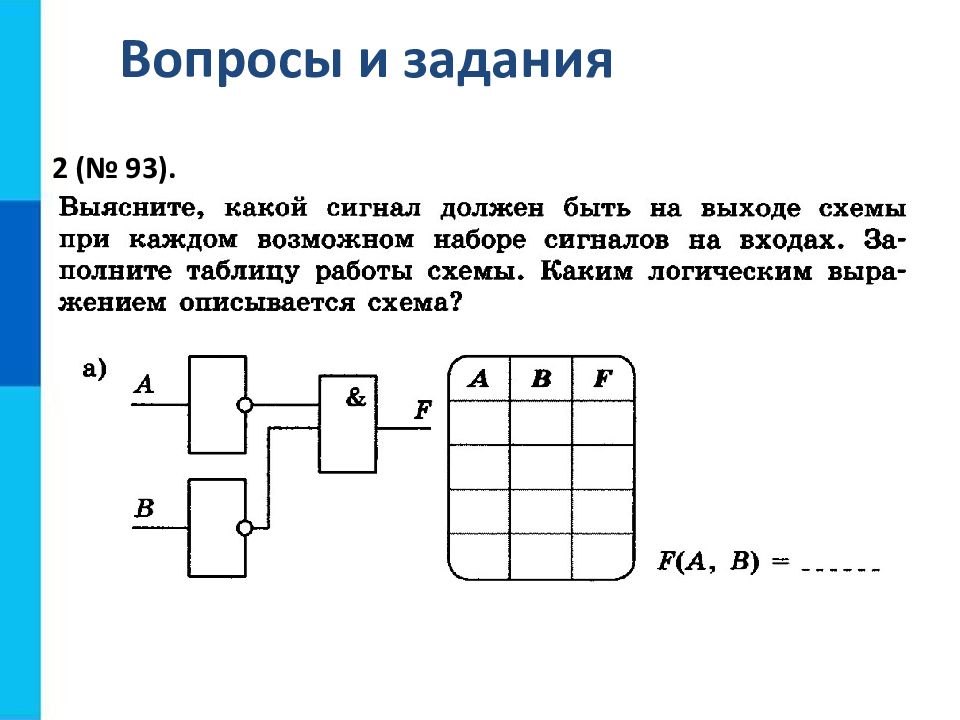
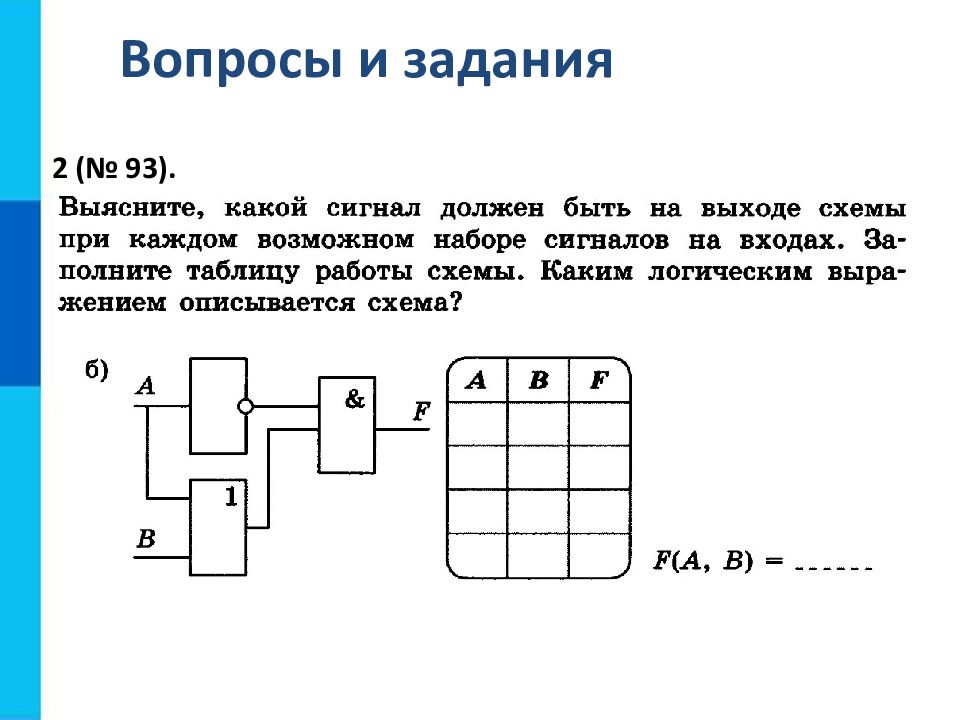
Вопросы и задания 1. Выясните, какой сигнал должен быть на выходе электронной схемы при каждом возможном наборе сигналов на входах. Составьте таблицу работы схемы. Каким логическим выражением описывается схема? 1 F А В
Вопросы и задания 2 (№ 93).
Вопросы и задания 2 (№ 93).
Вопросы и задания 3. Для какого из данных слов истинно высказывание: НЕ (ударение на первый слог) И (количество букв чётное)? 1) корова 2 ) козел 3) кошка 4) конь
Вопросы и задания 4. Для какого из указанных значений числа X истинно высказывание: ( X < 3) И НЕ (X < 2)? 1 ) 1 2) 2 3) 3 4) 4
Вопросы и задания 5. Найдите значения логических выражений: а) F = ( 0 0) (1 1) б ) F = 1&( 1 1) ( 0&1)
Вопросы и задания 6. Составьте таблицу истинности для следующих логических выражений : а ) F = (x& y) z б ) F = (x y)&(y x)
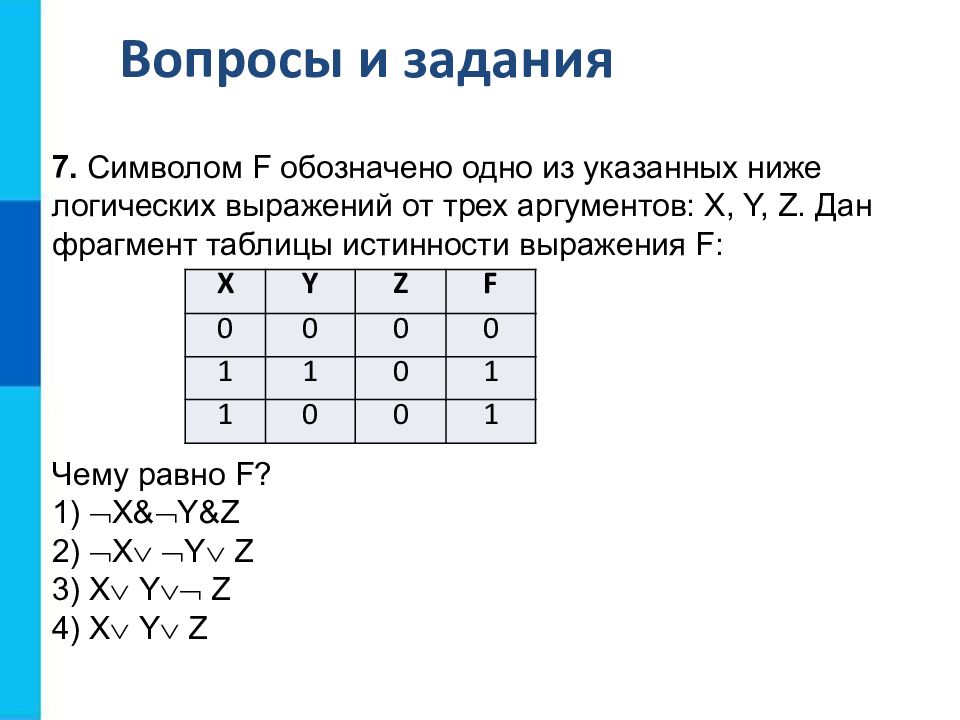
Вопросы и задания 7. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F : Чему равно F? 1) X & Y&Z 2) X Y Z 3) X Y Z 4) X Y Z X Y Z F 0 0 0 0 1 1 0 1 1 0 0 1
Вопросы и задания 8. Составьте логическую схему к выражению: F = ( A & B ) C
Вопросы и задания 9. Составьте логическое выражение по схеме:
Вопросы и задания Пример. Какое логическое выражение равносильно выражения ( A B ) C ? Решение. Логические выражения называются равносильными, если при любых значениях, входящих в них переменных, значения этих выражений равны. Преобразуем выражение ( A B ) в соответствии с законом до Моргана (законом общей инверсии): ( A B )= A ˄ B ), поэтому правилен ответ под номером 1.
Вопросы и задания 10.
Вопросы и задания 1 1.
Вопросы и задания 1 2.
Вопросы и задания 1 3.
Домашнее задание § 1.3; подготовка к контрольной работе
