А лгебра және геометрия
Берілген нүктесінен бірдей қашықтықта жатқан нүктелердің геометриялық орны шеңбер деп аталады. Анықтамада айтылған нүктесі шеңбердің центрі болады, ал бірдей қашықтық – оның радиусы болады, біз оны R арқылы белгілейміз. Шеңбердің нүктелерінің кез келгенін деп белгілейік, онда (1) 1. Шеңбер теңдеуі шеңбердің теңдеуі болады.
Жазықтықтың фокус деп аталатын берілген екі нүктесінен ара қашықтарының қосындысы тұрақты санға тең болатын нүктелерінің геометриялық орны эллипс деп аталады. Екі нүкте ара қашықтығын анықтайтын формуланы қолданып: болғандықтан, онда (2) эллипстің канондық теңдеуі
және сандары эллипстің үлкен және кіші жарты осьтері деп аталады. эллипстің эксцентриситеті деп аталады. Эллипс үшін. Егер болса, онда болады да, эллипс шеңберге айналады. эллипстің фокальдық радиус векторлары.
Мысал. теңдеуінен эллипстің канондық теңдеуін құрыңдар. Осы эллипстің жарты осьтерін және эксцентриситетін анықтаймыз. Ол үшін берілген теңдеуді түрлендіреміз эксцентриситеті Осыдан, онда жарты осьтері
3.Гипербола Жазықтықта фокус деп аталатын, берілген екі нүктесінен ара қашықтықтарының айырмасы тұрақты санға тең болатын нүктелерінің геометриялық орны гипербола деп аталады. болғандықтан, онда (3) гиперболаның канондық теңдеуі
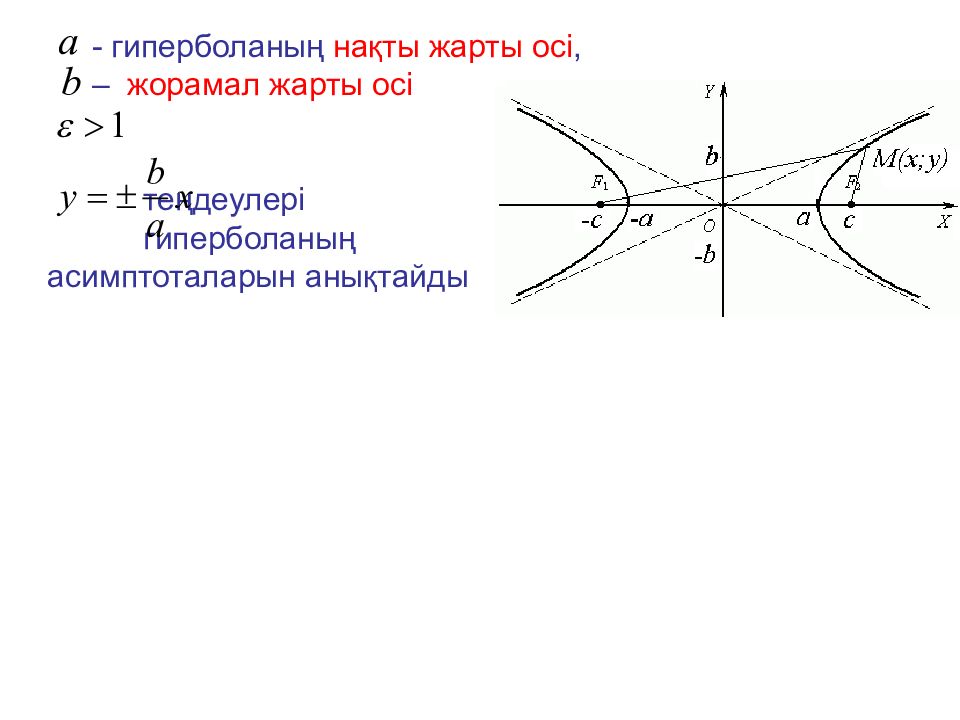
- гиперболаның нақты жарты осі, – жорамал жарты осі теңдеулері гиперболаның асимптоталарын анықтайды
Мысал. Айталық гиперболаның берілсін.
4. Парабола Фокус деп аталатын F нүктесінен және директриса делінетін түзуінен бірдей қашықтықта жатқан геометриялық нүктелерінің орнын парабола деп атайды. Анықтама бойынша (4) (4) - параболаның канондық теңдеуі деп аталады.
- парабола директрисасының теңдеуі ( 5 ) Егер директриса ОУ осіне перпендикуляр болып және фокусы осы осьте орналасса онда параболаның теңдеуі (4) ОХ осіне симметриялы, ал (5) ОУ осіне симметриялы параболалар. Параболаның эксцентриситеті
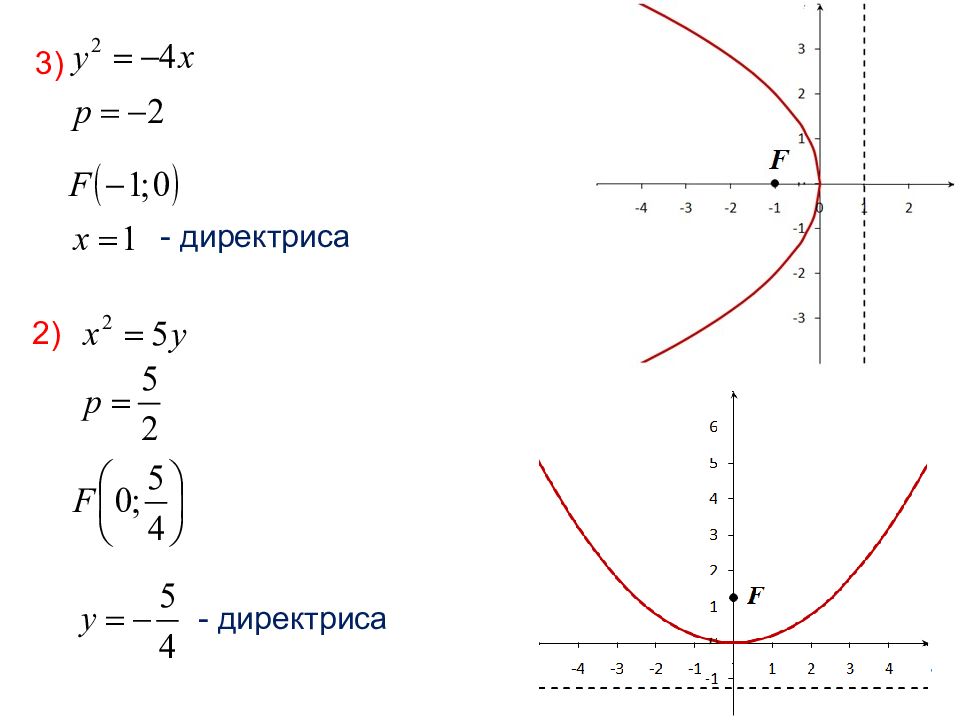
Мысал. Келесі параболалар үшін параметр шамасы мен координаттық осьтердің орналасуын анықтаңыздар. 1) у 2 = 6 х ; 2) х 2 = 5 у ; 3) у 2 = - 4 х ; 4) х 2 = - у. 1) - директриса
3) - директриса 2) - директриса
