Первый слайд презентации
ГОТОВИМСЯ к ГИА 2014 геометрические задачи на доказательство ( 2 часть)
Слайд 3: Содержание
Приведено решение – 16 задач Для самостоятельной работы – 6 задач
Слайд 4: Докажите, что биссектрисы смежных углов перпендикулярны
Доказательство. ‹1+ ‹2 + ‹3 + ‹4=180 º т.к. ‹1=‹2, а ‹3=‹4, то 2(‹2)+2(‹4)=180 º 2(‹2+‹4)=180 º ‹2+‹4 = 90 º Значит биссектрисы перпендикулярны. 1 2 3 4 :2
то BЕ = KD, CF = AM. В параллелограмме противоположные углы равны, то треугольники EBF и KDM, FCK и MAE равны по двум сторонам и углу между ними. Из равенства треугольников следует, что EF=MK, EM=FK. Так как противоположные стороны четырехугольника EFKM равны, то по признаку параллелограмма данный четырехугольник является параллелограммом. Доказательство : Так как в параллелограмме противоположные стороны равны и по условию известно, что АЕ = CK, BF = DM,
Доказательство: ∆АВК=∆СВК по двум сторонам и углу между ними. Значит ‹3=‹4, т.к. лежат в равных треугольниках против равных сторон т.е. ВК является биссектрисой. А В С К 1 2 3 4
Слайд 7: В окружности с центром О проведены две хорды АВ и CD так, что центральные углы АОВ и СОD равны. На эти хорды опущены перпендикуляры ОК и OL. Докажите, что ОК и OL равны
Доказательство : 1) ∆ АОВ = ∆ СОD по двум сторонам и углу между ними 2) AO = BO = CO = DO как радиусы окружности, 3) ‹ AOB = ‹ COD - по условию. Следовательно, высоты OK и OL равны как соответственные элементы равных треугольников.
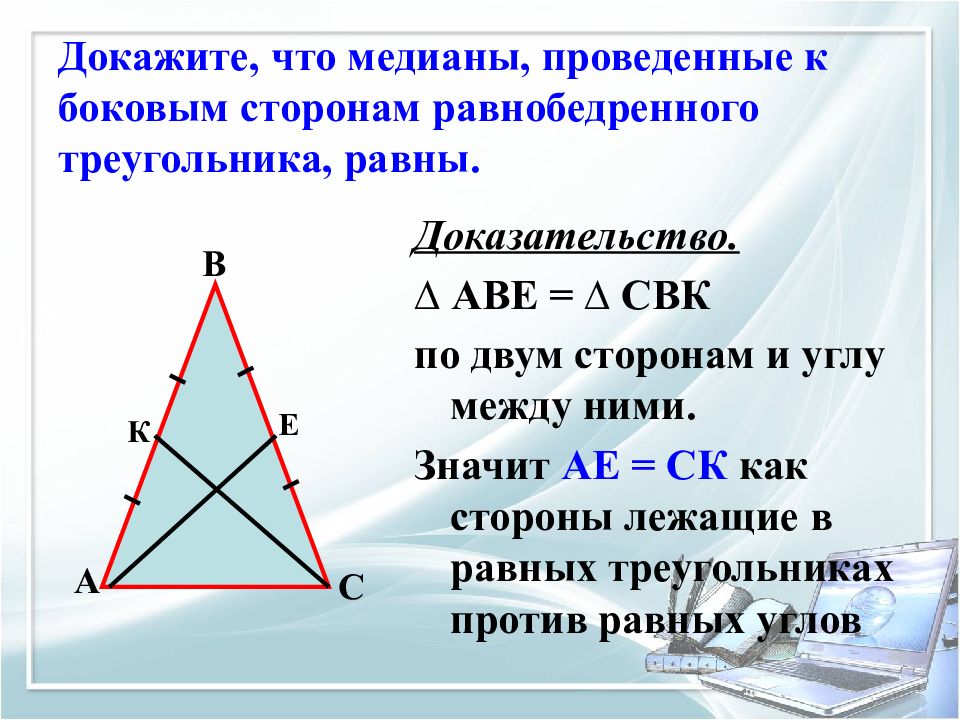
Слайд 8: Докажите, что медианы, проведенные к боковым сторонам равнобедренного треугольника, равны
Доказательство. ∆ АВЕ = ∆ СВК по двум сторонам и углу между ними. Значит АЕ = СК как стороны лежащие в равных треугольниках против равных углов А В С К Е
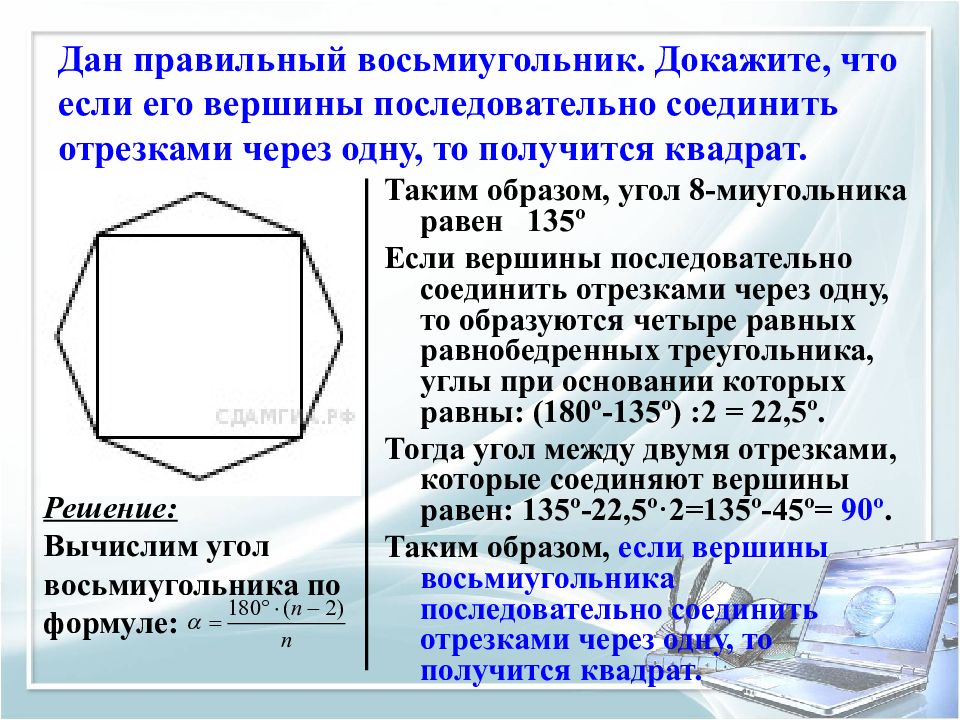
Слайд 9: Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат
Таким образом, угол 8-миугольника равен 135 º Если вершины последовательно соединить отрезками через одну, то образуются четыре равных равнобедренных треугольника, углы при основании которых равны: (180 º -135 º ) :2 = 22,5 º. Тогда угол между двумя отрезками, которые соединяют вершины равен: 135 º -22,5 º· 2=135 º -45 º = 90 º. Таким образом, если вершины восьмиугольника последовательно соединить отрезками через одну, то получится квадрат. Решение: Вычислим угол восьмиугольника по формуле:
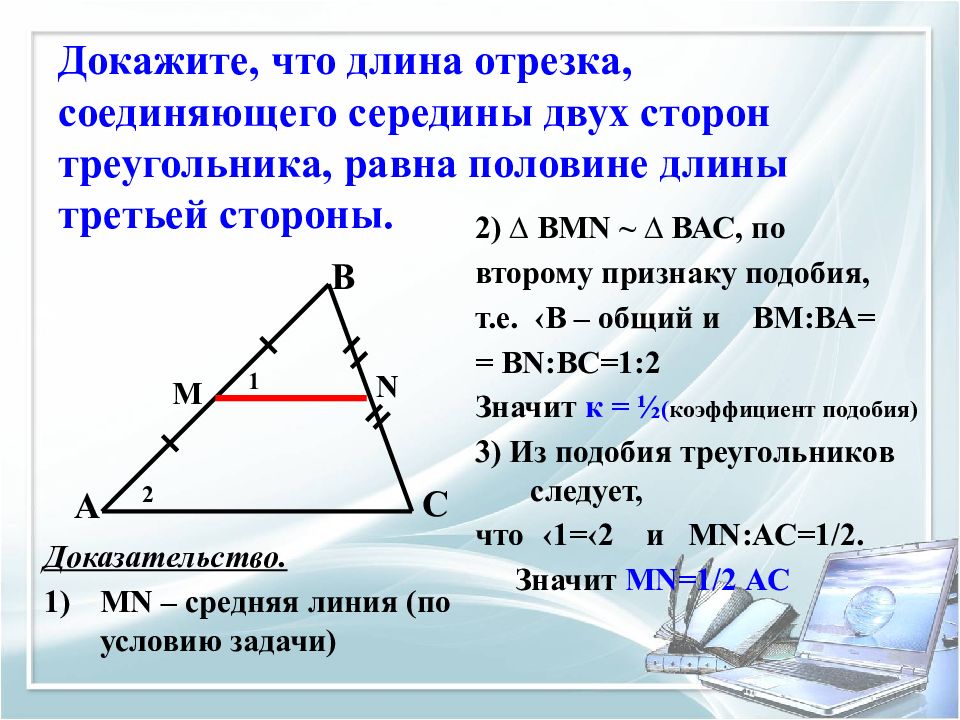
Слайд 10: Докажите, что длина отрезка, соединяющего середины двух сторон треугольника, равна половине длины третьей стороны
Доказательство. MN – средняя линия (по условию задачи) 2) ∆ ВМ N ~ ∆ ВАС, по второму признаку подобия, т.е. ‹В – общий и ВМ:ВА= = В N :ВС=1:2 Значит к = ½ ( коэффициент подобия) 3) Из подобия треугольников следует, что ‹1=‹2 и М N :АС=1/2. Значит М N =1/2 АС А В С M N 2 1
Слайд 11: Докажите, что если две хорды АВ и С D пересекаются в т.Е, то произведение длин отрезков одной хорды равно произведению отрезков другой хорды: АЕ · ЕВ = СЕ · Е D
Доказательство. В треугольниках А D Е и СВЕ : а) ‹1 = ‹2 (как вписанные углы, опирающиеся на одну и ту же дугу В D ) б) ‹3=‹4 (как вертикальные) Т.е. ∆А D Е ~∆ СВЕ (по двум углам) Значит: АЕ:СЕ= D Е:ВЕ, или АЕ · ЕВ = СЕ · Е D О D В А С Е 1 2 3 4
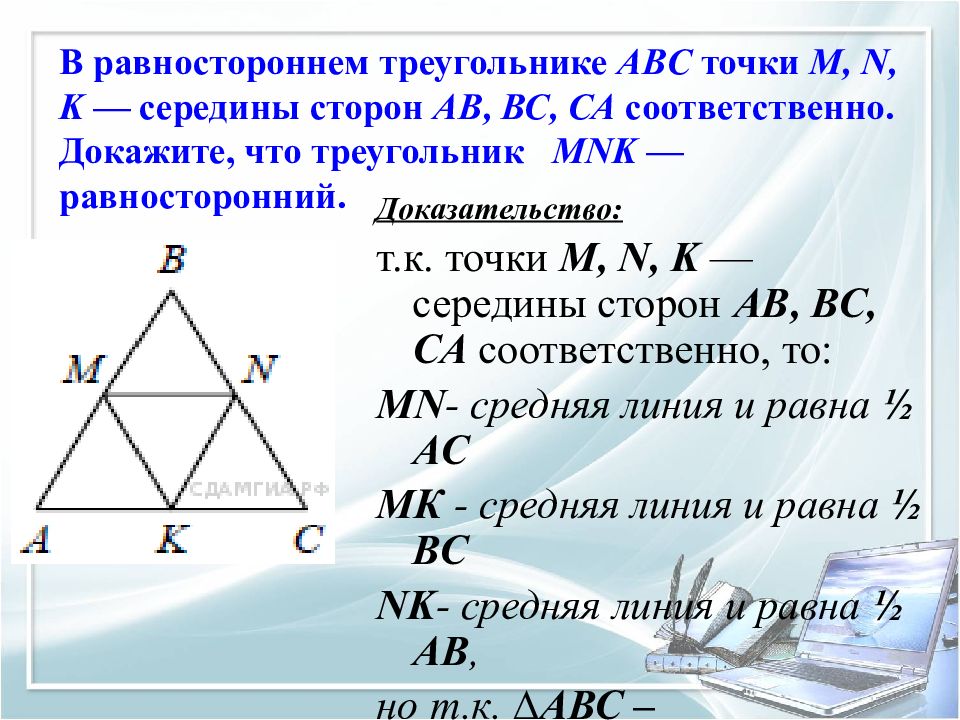
Слайд 12: В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний
Доказательство: т.к. точки M, N, K — середины сторон АВ, ВС, СА соответственно, то: MN - средняя линия и равна ½ АС МК - средняя линия и равна ½ ВС NK - средняя линия и равна ½ АВ, но т.к. ∆АВС – равносторонний, то и ∆MNK — равносторонний.
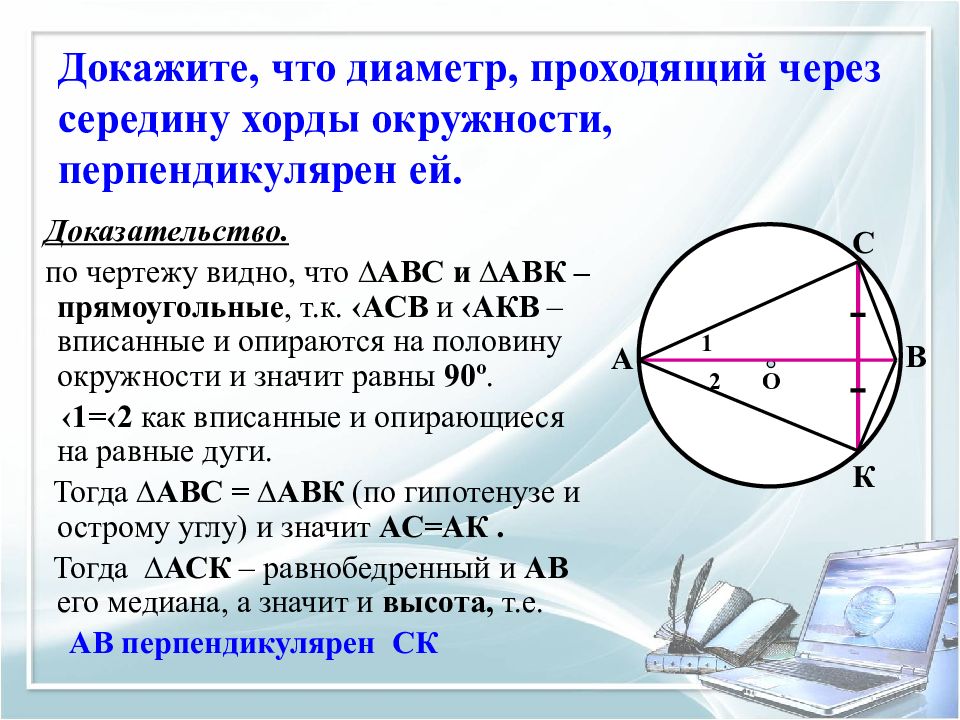
Слайд 13: Докажите, что диаметр, проходящий через середину хорды окружности, перпендикулярен ей
Доказательство. по чертежу видно, что ∆АВС и ∆АВК – прямоугольные, т.к. ‹АСВ и ‹АКВ – вписанные и опираются на половину окружности и значит равны 90 º. ‹1=‹2 как вписанные и опирающиеся на равные дуги. Тогда ∆АВС = ∆АВК (по гипотенузе и острому углу) и значит АС=АК. Тогда ∆АСК – равнобедренный и АВ его медиана, а значит и высота, т.е. АВ перпендикулярен СК О А В С К 1 2
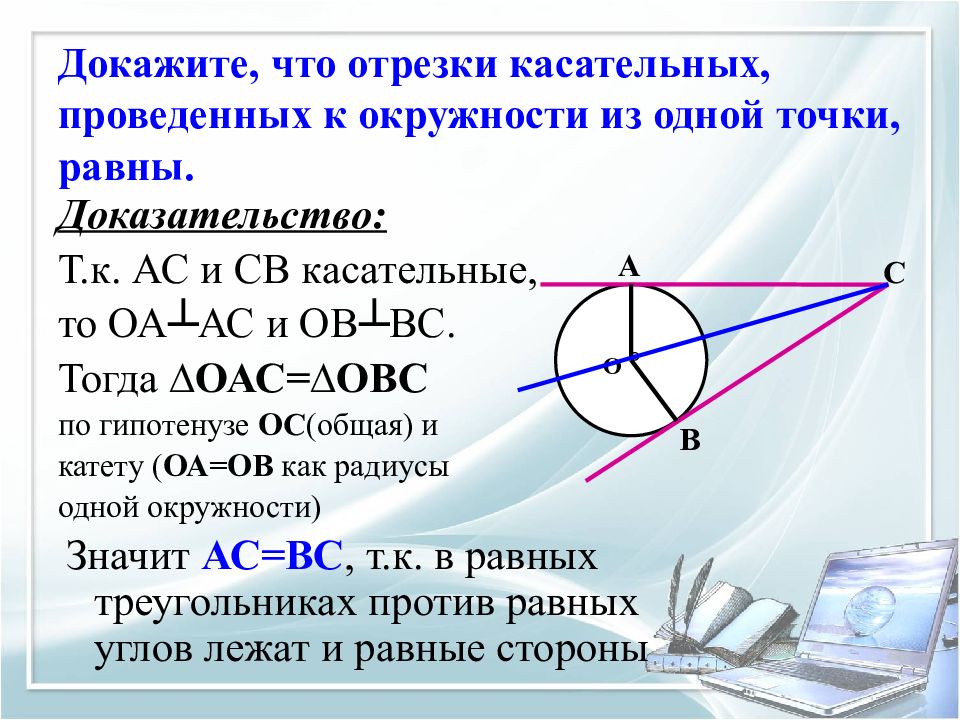
Слайд 14: Докажите, что отрезки касательных, проведенных к окружности из одной точки, равны
Доказательство: Т.к. АС и СВ касательные, то ОА┴АС и ОВ┴ВС. Тогда ∆ОАС=∆ОВС по гипотенузе ОС (общая) и катету ( ОА=ОВ как радиусы одной окружности) Значит АС=ВС, т.к. в равных треугольниках против равных углов лежат и равные стороны О А В С
Слайд 15: Докажите что, градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается
Доказательство: Проведём диаметр ВК. Тогда ‹1 будет внешним углом ∆АОВ и ‹1= ‹2+‹3, но ‹2= ‹3 как углы при основании равнобедренного ∆АОВ Т.е. ‹1=2 ·‹ 3 => ‹3= ½·‹ 1, но т.к. ‹1 - центральный, то ‹1= ں АК; ‹3= ½· ں АК Аналогично: ‹6= ½· ں СК Значит ‹3+‹6 = ½· ں АК+ ½· ں СК= ½· ( ں АК+ ں СК)= = ½· ں АС, т.е вписанный угол АВС= ½· ں АС О А В С К 1 2 3 4 5 6
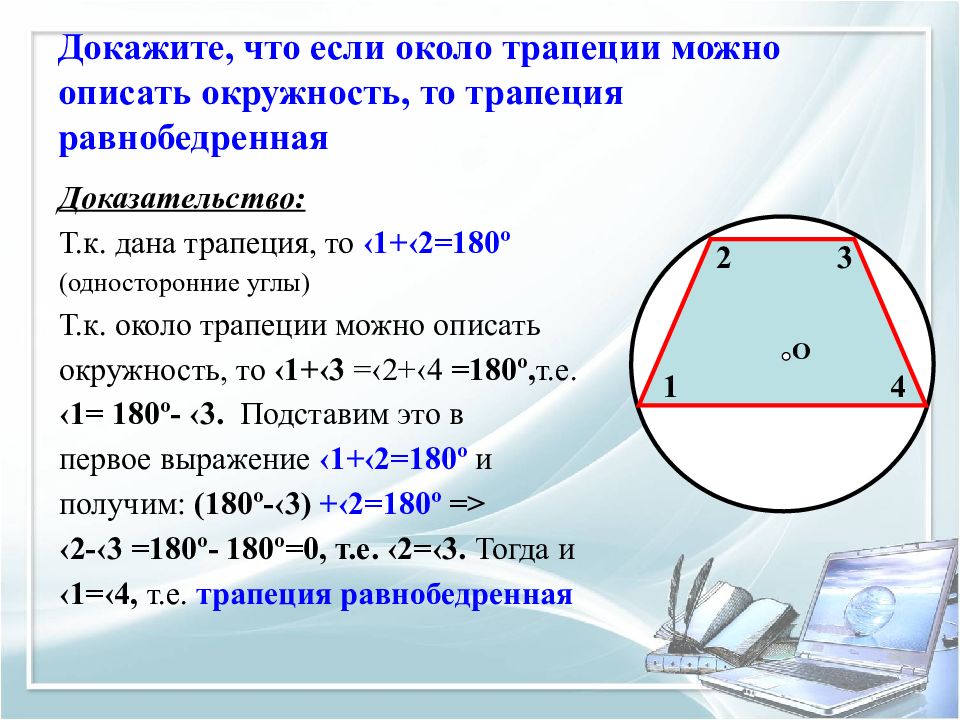
Слайд 16: Докажите, что если около трапеции можно описать окружность, то трапеция равнобедренная
Доказательство: Т.к. дана трапеция, то ‹1+‹2=180 º (односторонние углы) Т.к. около трапеции можно описать окружность, то ‹1+‹3 =‹2+‹4 =180 º, т.е. ‹1= 180 º - ‹ 3. Подставим это в первое выражение ‹1+‹2=180 º и получим: (180 º - ‹ 3) +‹2=180 º => ‹2- ‹ 3 =180 º - 180 º =0, т.е. ‹2= ‹ 3. Тогда и ‹1=‹4, т.е. трапеция равнобедренная О 1 2 3 4
Слайд 17: Докажите, что если две окружности имеют общую хорду, то прямая, проходящая через центры этих окружностей, перпендикулярна данной хорде
Доказательство: ∆О 1 АО 2 =∆О 1 ВО 2 по трем сторонам (О1О2 – общая; О1А=О1В как радиусы одной окружности О1; О2А=О2В как радиусы окружностьО2). Значит ‹1=‹2. Тогда биссектриса О 1 К в равнобедренном треугольнике О 1 АВ является и высотой, т.е. О 1 О 2 ┴АВ О 1 О 2 А В К 1 2
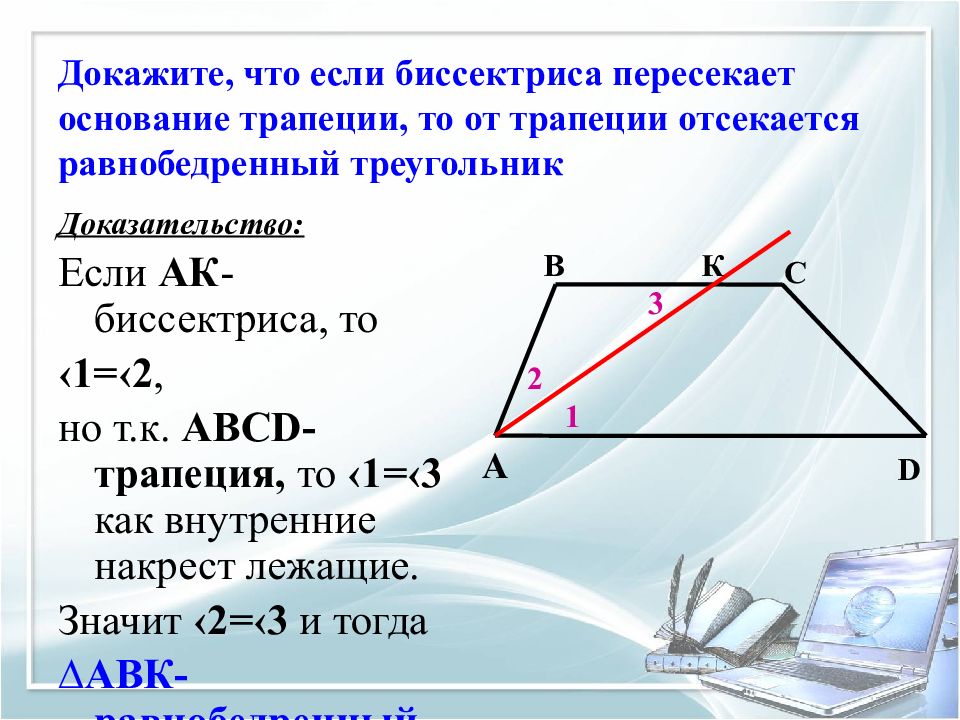
Слайд 18: Докажите, что если биссектриса пересекает основание трапеции, то от трапеции отсекается равнобедренный треугольник
Доказательство: Если АК -биссектриса, то ‹1=‹2, но т.к. АВС D -трапеция, то ‹1=‹3 как внутренние накрест лежащие. Значит ‹2=‹3 и тогда ∆АВК-равнобедренный А В С D К 1 2 3
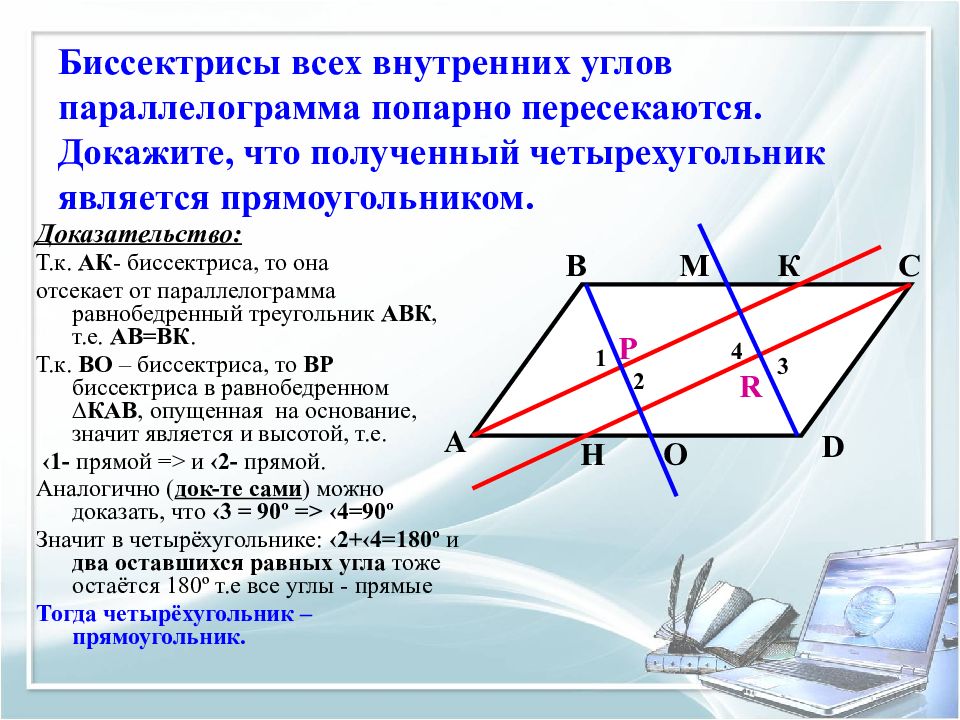
Доказательство: Т.к. АК - биссектриса, то она отсекает от параллелограмма равнобедренный треугольник АВК, т.е. АВ=ВК. Т.к. ВО – биссектриса, то ВР биссектриса в равнобедренном ∆КАВ, опущенная на основание, значит является и высотой, т.е. ‹1- прямой => и ‹2- прямой. Аналогично ( док-те сами ) можно доказать, что ‹3 = 90 º => ‹ 4=90 º Значит в четырёхугольнике: ‹2+‹4=180 º и два оставшихся равных угла тоже остаётся 180 º т.е все углы - прямые Тогда четырёхугольник – прямоугольник. А В С D М К О Н Р R 1 2 3 4
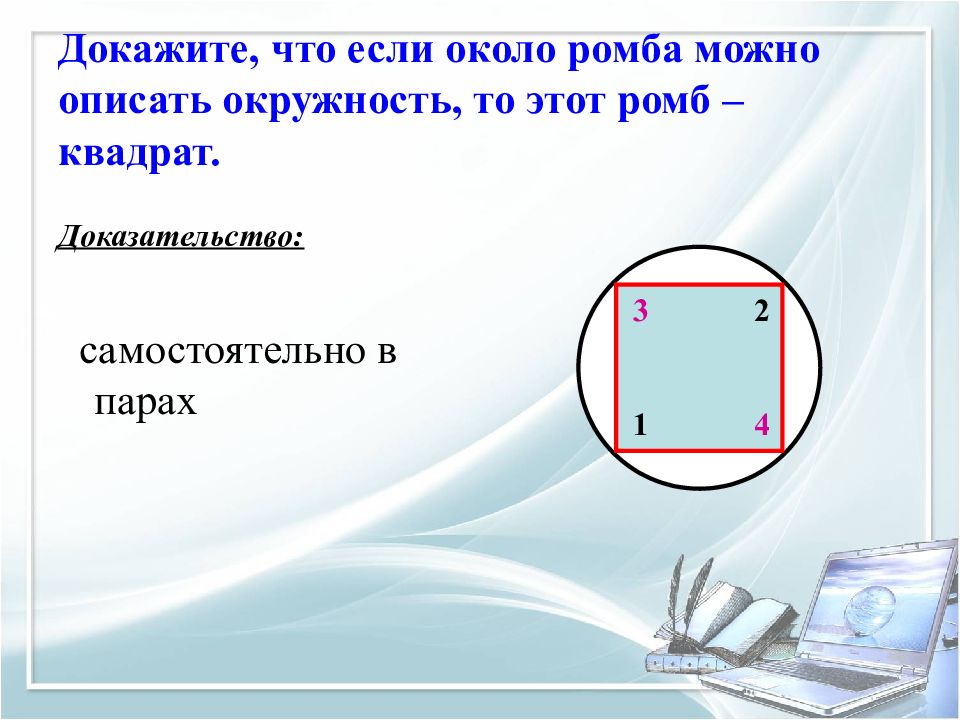
Слайд 20: Докажите, что если около ромба можно описать окружность, то этот ромб – квадрат
Доказательство: самостоятельно в парах 1 2 3 4
Слайд 21: Докажите, что средняя линия трапеции равна полусумме её оснований
Доказательство: самостоятельно или стр.210 в учебнике по геометрии 7-9 А.С. Атанасяна
Слайд 22: Докажите, что если в равнобедренную трапецию можно вписать окружность, то высота равна средней линии
Доказательство: самостоятельно
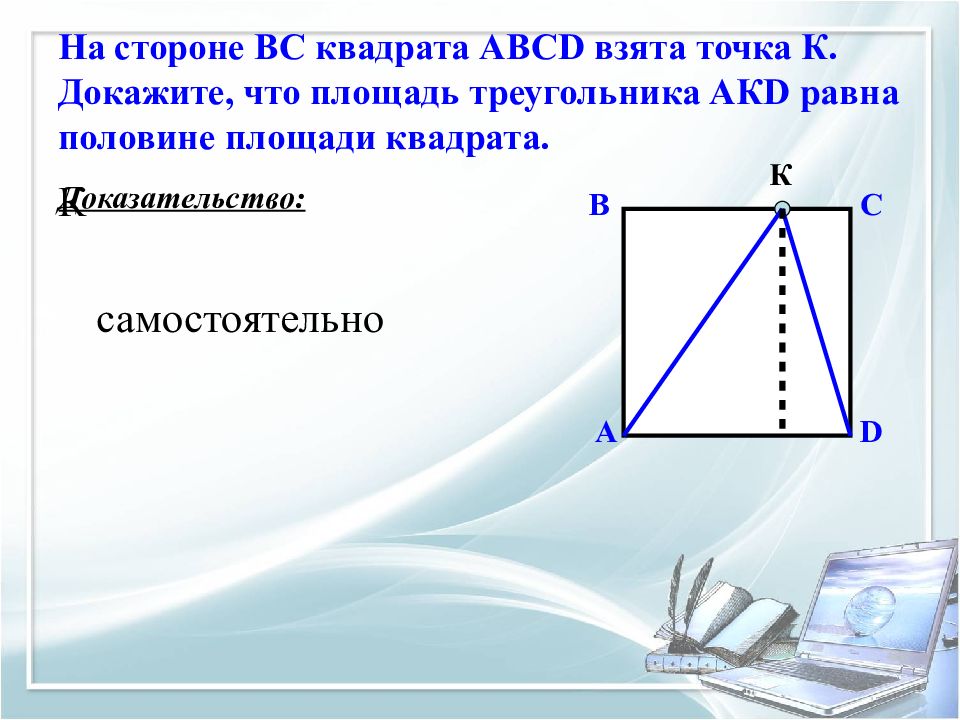
Слайд 23: На стороне ВС квадрата АВС D взята точка К. Докажите, что площадь треугольника АК D равна половине площади квадрата
Доказательство: К К А В С D самостоятельно
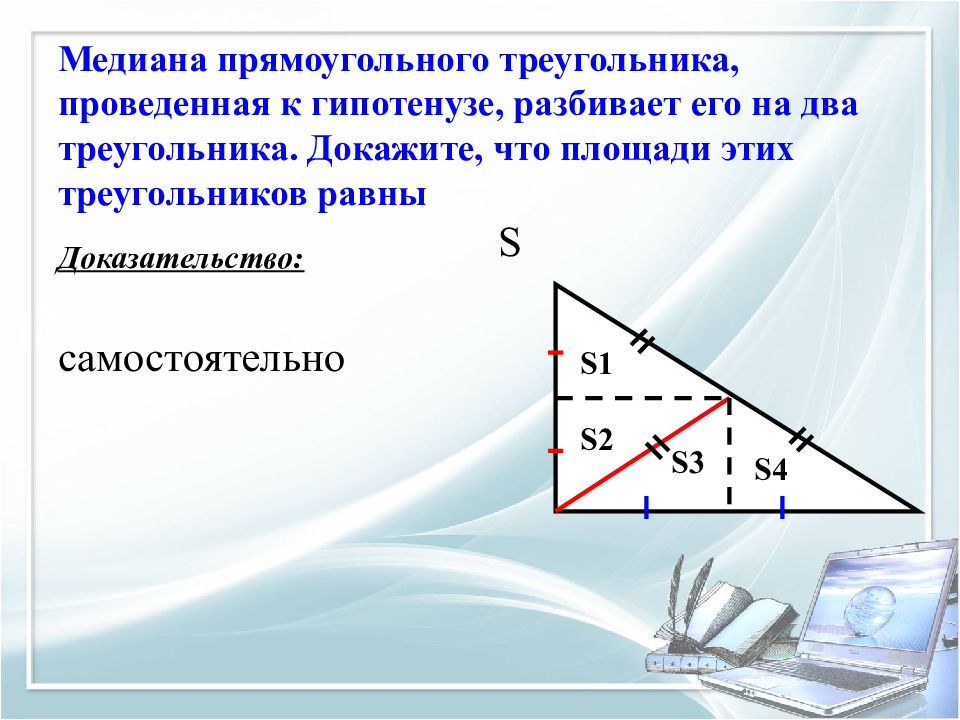
Слайд 24: Медиана прямоугольного треугольника, проведенная к гипотенузе, разбивает его на два треугольника. Докажите, что площади этих треугольников равны
Доказательство: самостоятельно S S1 S2 S4 S3
Слайд 25: Докажите, что биссектрисы, проведенные из вершин основания равнобедренного треугольника, равны
Доказательство: самостоятельно