Первый слайд презентации: Подобие треугольников
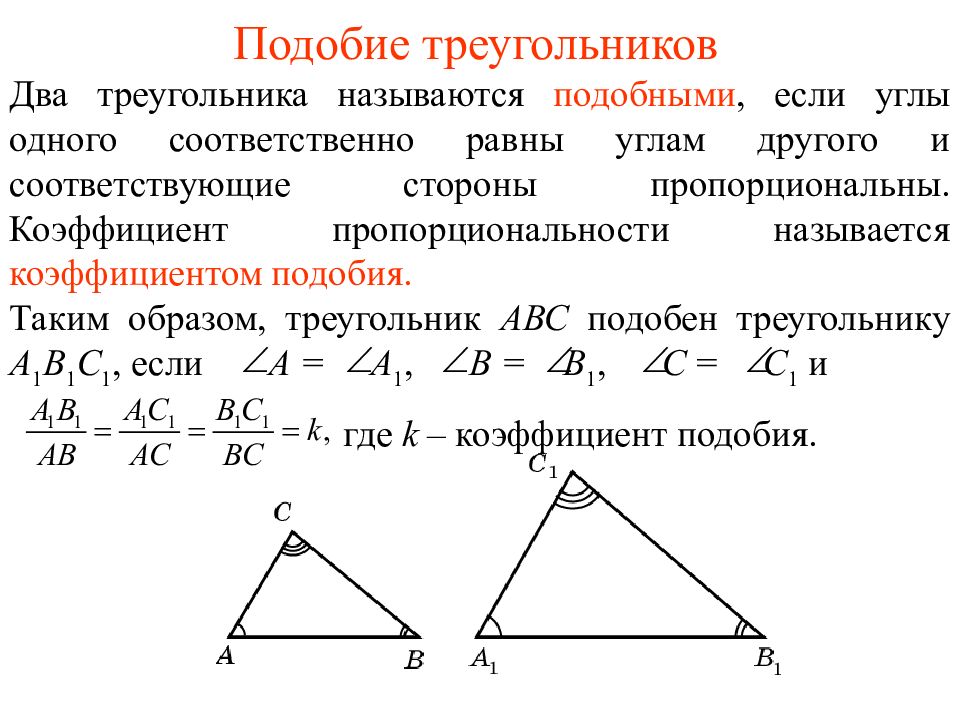
Два треугольника называются подобными, если углы одного соответственно равны углам другого и соответствующие стороны пропорциональны. Коэффициент пропорциональности называется коэффициентом подобия. Таким образом, треугольник АВС подобен треугольнику A 1 В 1 С 1, если A = A 1, B = B 1, C = C 1 и где k – коэффициент подобия.
Слайд 2: Первый признак подобия
Теорема. (Первый признак подобия.) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. Отложим на луче А 1 В 1 отрезок А 1 В', равный АВ, и проведем прямую В'С', параллельную В 1 С 1. Треугольники А 1 B ' C ' и АВС равны (по второму признаку равенства треугольников). По теореме о пропорциональных отрезках имеет место равенство С ледовательно, имеем равенство Аналогичным образом доказывается, что имеет место равенство Следовательно, треугольники подобны. Доказательство. Пусть в треугольниках АВС и А 1 В 1 С 1 A = A 1, B = B 1. Тогда и C = C 1. Докажем, что.
Слайд 3: Вопрос 1
Какие треугольники называются подобными? Ответ: Два треугольника называются подобными, если углы одного соответственно равны углам другого и соответствующие стороны пропорциональны.
Слайд 4: Вопрос 2
Сформулируйте первый признак подобия треугольников. Ответ: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Слайд 5: Вопрос 3
Подобны ли любые два: а) равносторонних треугольника; б) равнобедренных треугольника; в) равнобедренных прямоугольных треугольника? Ответ: а) Да; б) нет ; в ) да.
Слайд 6: Упражнение 1
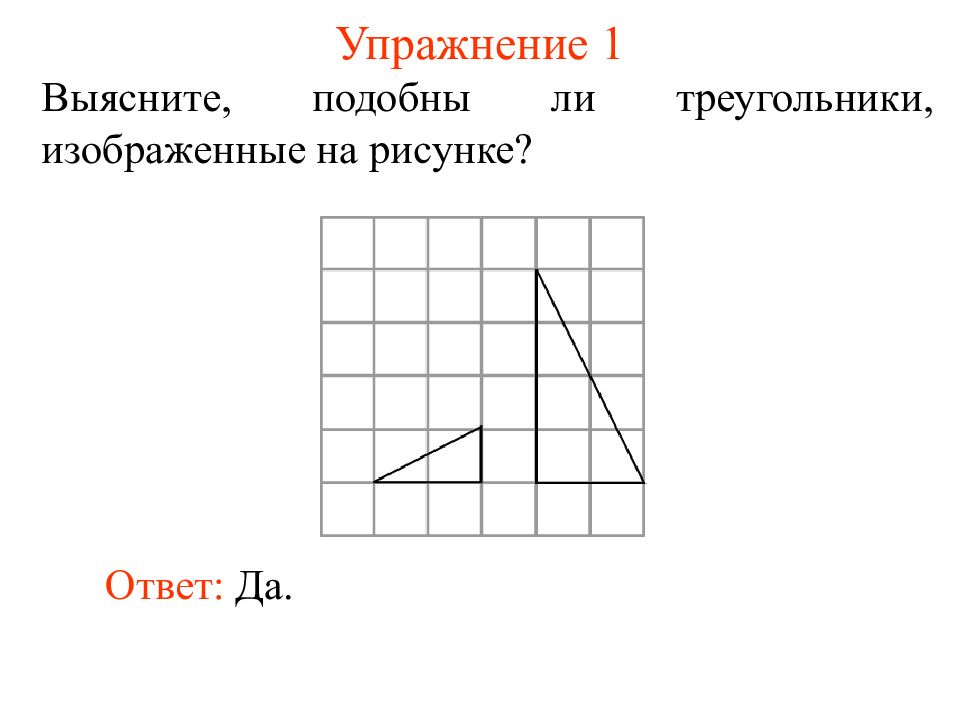
Выясните, подобны ли треугольники, изображенные на рисунке? Ответ: Да.
Слайд 7: Упражнение 2
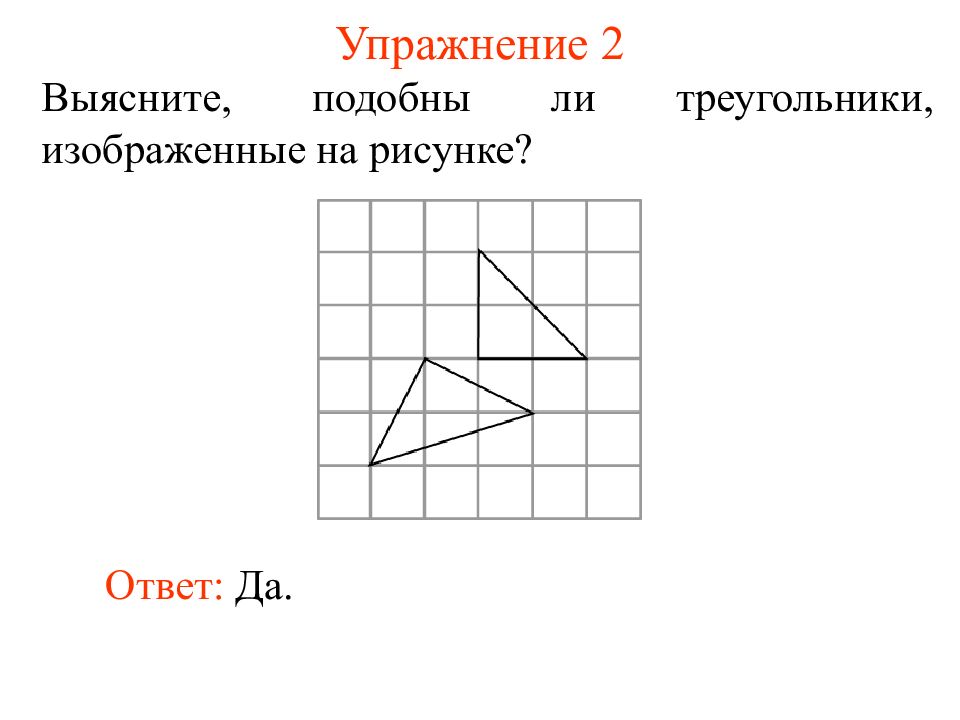
Выясните, подобны ли треугольники, изображенные на рисунке? Ответ: Да.
Слайд 8: Упражнение 3
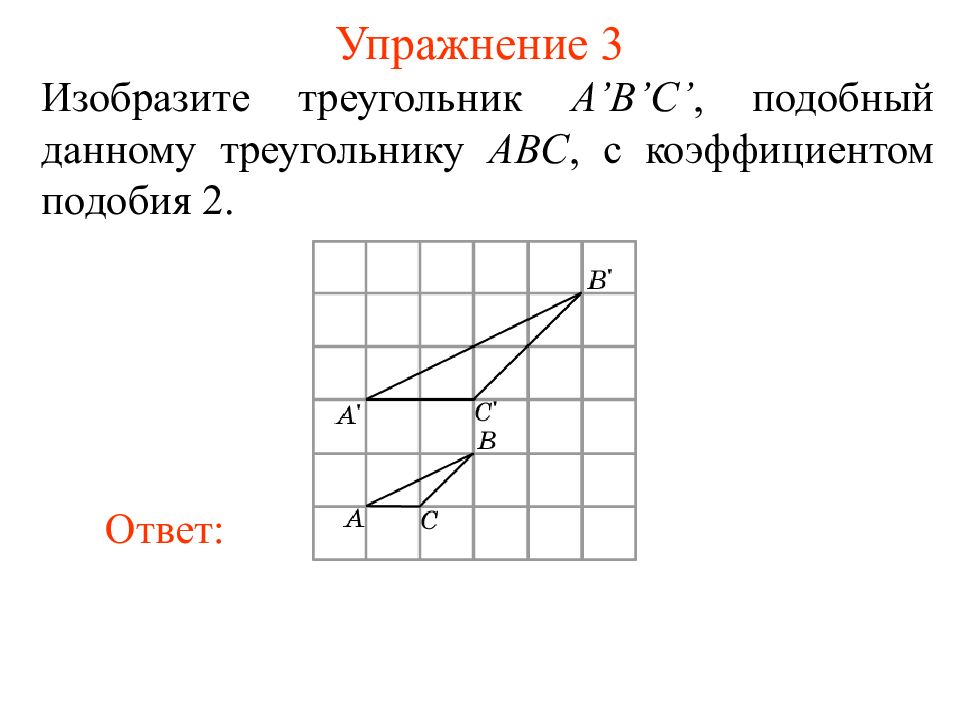
Изобразите треугольник A’B’C’, подобный данному треугольнику ABC, с коэффициентом подобия 2. Ответ:
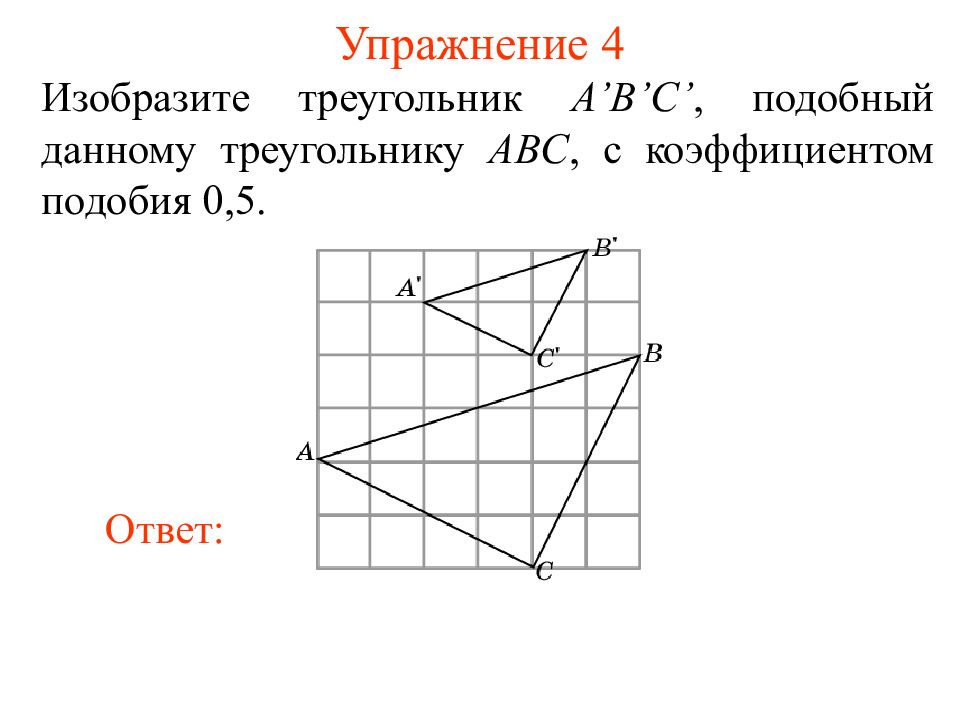
Слайд 9: Упражнение 4
Изобразите треугольник A’B’C’, подобный данному треугольнику ABC, с коэффициентом подобия 0,5. Ответ:
Слайд 10: Упражнение 5
Стороны треугольника равны 5 см, 8 см и 10 см. Найдите стороны подобного ему треугольника, если коэффициент подобия равен: а) 0,5 ; б) 2. Ответ: а) 2,5 см, 4 см и 5 см; б) 10 см, 16 см и 20 см.
Слайд 11: Упражнение 6
Подобны ли прямоугольные треугольники, если у одного из них есть угол 40 о, а у другого 50 о ? Ответ: Да.
Слайд 12: Упражнение 7
Два треугольника подобны. Два угла одного треугольника равны 55 о и 80 о. Найдите наименьший угол второго треугольника. Ответ: 45 о.
Слайд 13: Упражнение 8
В подобных треугольниках АВС и А 1 В 1 С 1 АВ = 8 см, ВС = 10 см, А 1 В 1 = 5,6 см, А 1 С 1 = 10,5 см. Найдите АС и В 1 С 1. Ответ: AC = 15 см, B 1 C 1 = 7 см.
Слайд 14: Упражнение 9
Ответ: AC = 4 м, B 1 C 1 = 14 м. У треугольников АВС и А 1 В 1 С 1 A = A 1, B = B 1, АВ = 5 м, ВС = 7 м, А 1 В 1 = 10 м, А 1 С 1 = 8 м. Найдите остальные стороны треугольников.
Слайд 15: Упражнение 10
Стороны треугольника относятся как 5:3:7. Найдите стороны подобного ему треугольника, у которого: а) периметр равен 45 см; б) меньшая сторона равна 5 см; в) большая сторона равна 7 см; г) разность большей и меньшей сторон составляет 2 см. Ответ: а) 15 см, 9 см, 21 см; в) 5 см, 3 см, 7 см; г) 2,5 см, 1,5 см, 3,5 см. б) 8 см, 5 см, 11 см;
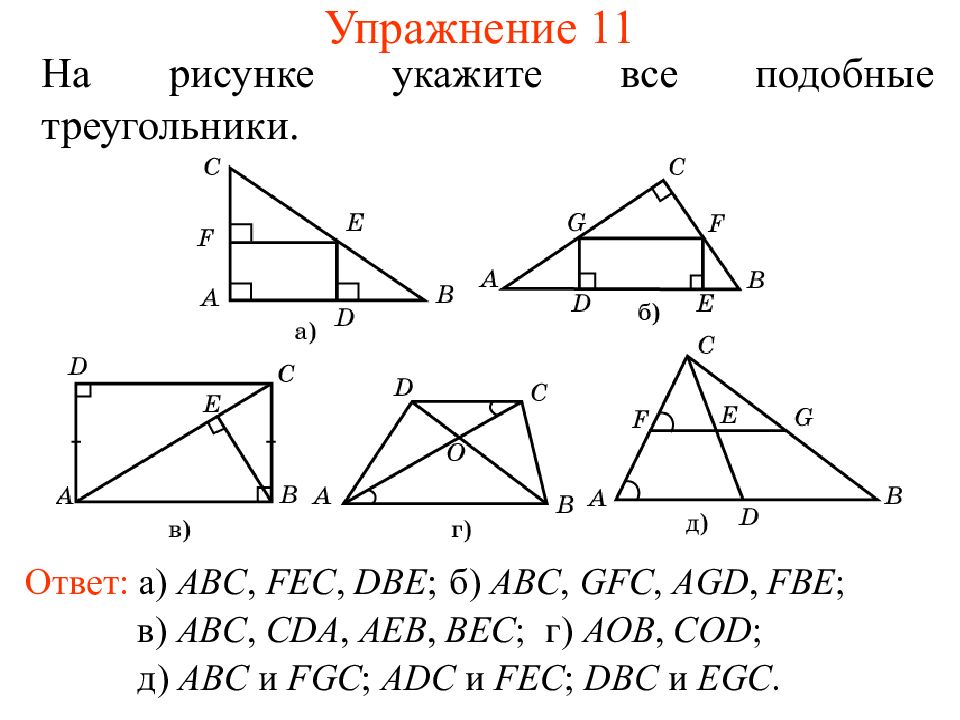
Слайд 16: Упражнение 11
На рисунке укажите все подобные треугольники. Ответ: а) ABC, FEC, DBE ; б) ABC, GFC, AGD, FBE ; в) ABC, CDA, AEB, BEC ; г) AOB, COD ; д) ABC и FGC ; ADC и FEC ; DBC и EGC.
Слайд 17: Упражнение 12
У двух равнобедренных треугольников углы между боковыми сторонами равны. Боковая сторона и основание одного треугольника равны соответственно 17 см и 10 см, основание другого равно 8 см. Найдите его боковую сторону. Ответ: 13,6 см.
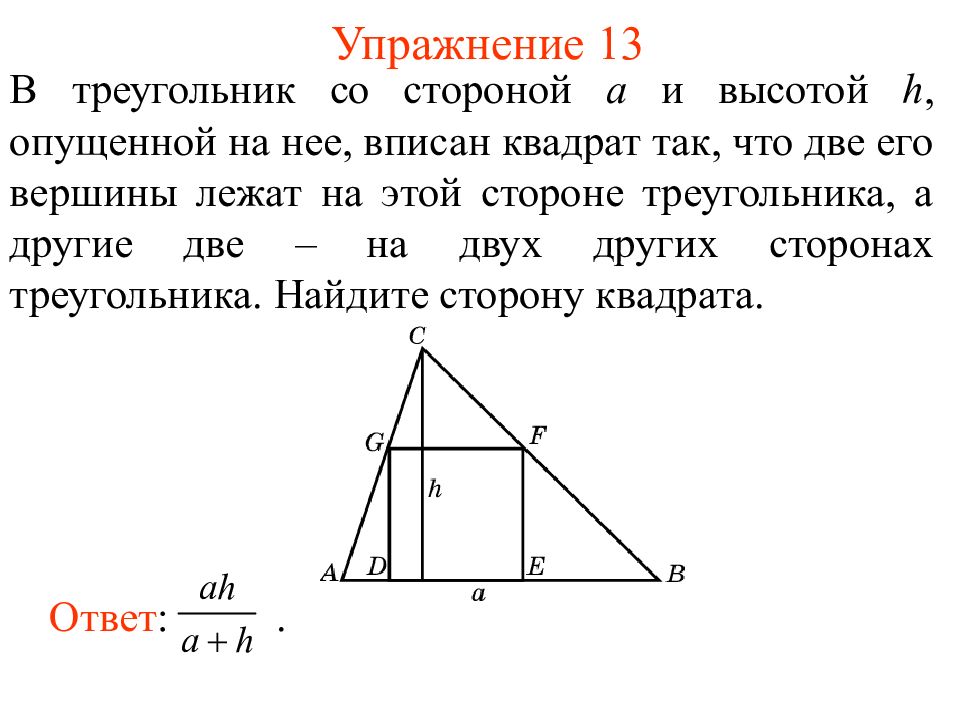
Слайд 18: Упражнение 13
В треугольник со стороной а и высотой h, опущенной на нее, вписан квадрат так, что две его вершины лежат на этой стороне треугольника, а другие две – на двух других сторонах треугольника. Найдите сторону квадрата. Ответ :.
Слайд 19: Упражнение 14
В треугольник АВС вписан ромб ADEF так, что угол А у них общий, а вершина Е находится на стороне ВС. Найдите сторону ромба, если АВ = с и АС = b. Ответ :.
Слайд 20: Упражнение 15
Можно ли треугольник пересечь прямой, непараллельной основанию, так, чтобы отсечь от него подобный треугольник? В каком случае это невозможно? Ответ: Можно, если треугольник неравносторонний.
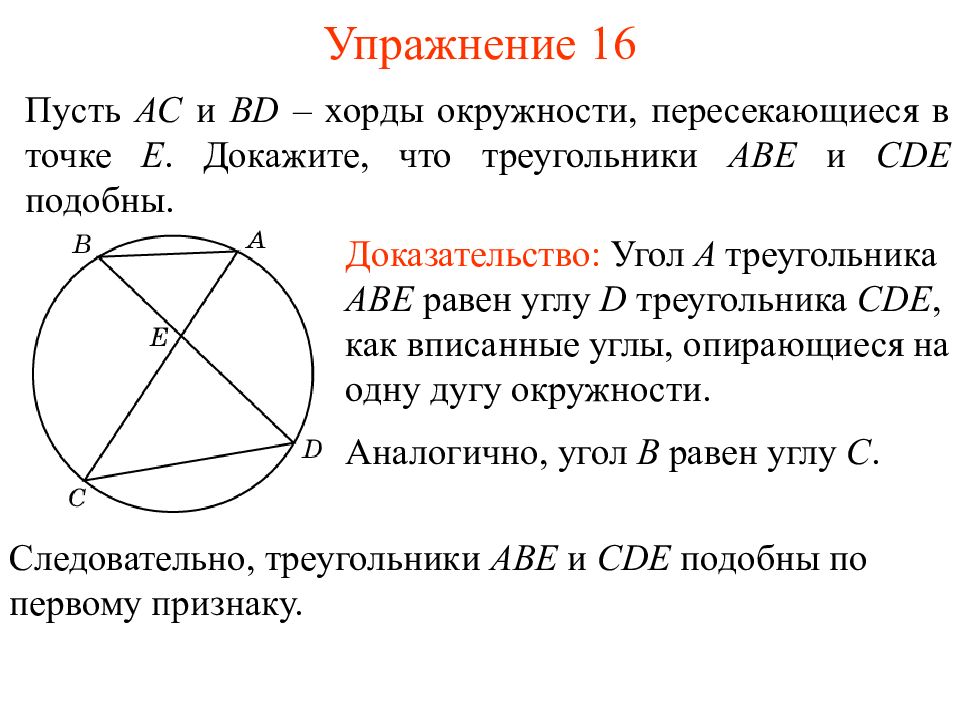
Слайд 21: Упражнение 16
Пусть AC и BD – хорды окружности, пересекающиеся в точке E. Докажите, что треугольники ABE и CDE подобны. Доказательство: Угол A треугольника ABE равен углу D треугольника CDE, как вписанные углы, опирающиеся на одну дугу окружности. Аналогично, угол B равен углу C. Следовательно, треугольники ABE и CDE подобны по первому признаку.
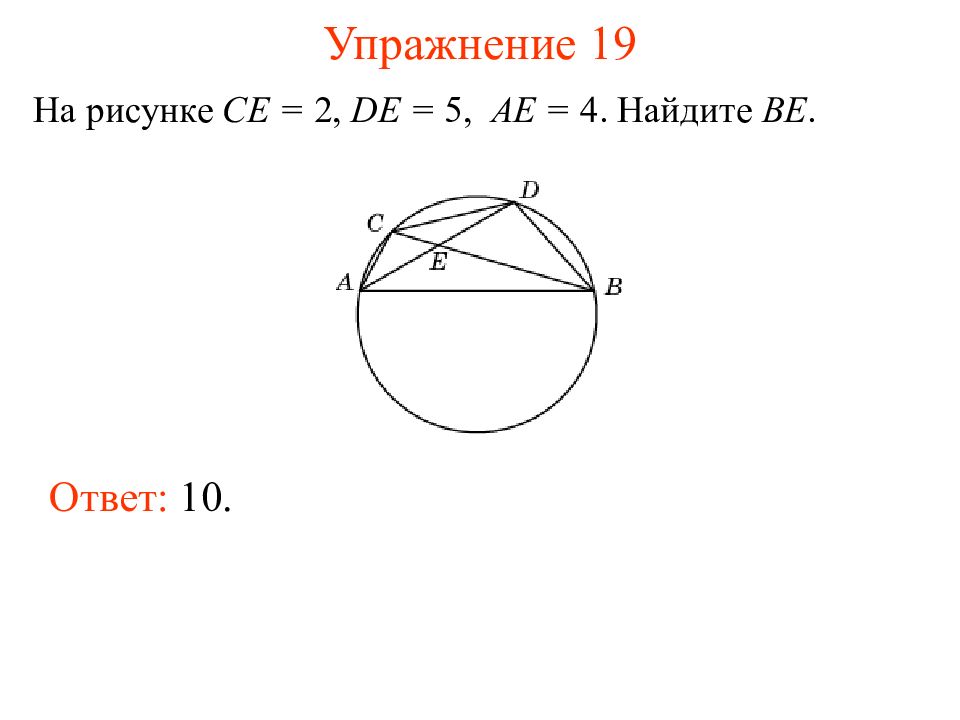
Слайд 24: Упражнение 19
На рисунке CE = 2, DE = 5, AE = 4. Найдите BE. Ответ: 10.
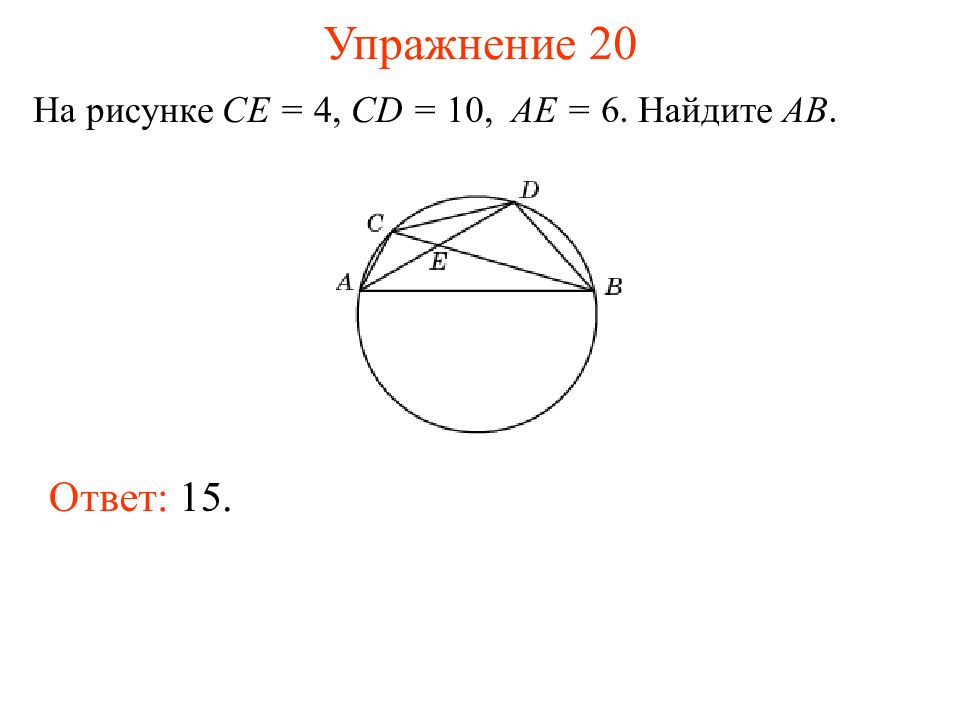
Слайд 25: Упражнение 20
На рисунке CE = 4, CD = 10, AE = 6. Найдите AB. Ответ: 15.
Слайд 26: Упражнение 21
Ответ: DEK и DLF, DEK и ELK, DLF и ELK, DFK и DLE, DFK и FLK, DLE и FLK. На рисунке DL – биссектриса треугольника DEF, вписанного в окружность. DL пересекает окружность в точке K, которая соединена отрезками с вершинами E и F треугольника. Найдите подобные треугольники.
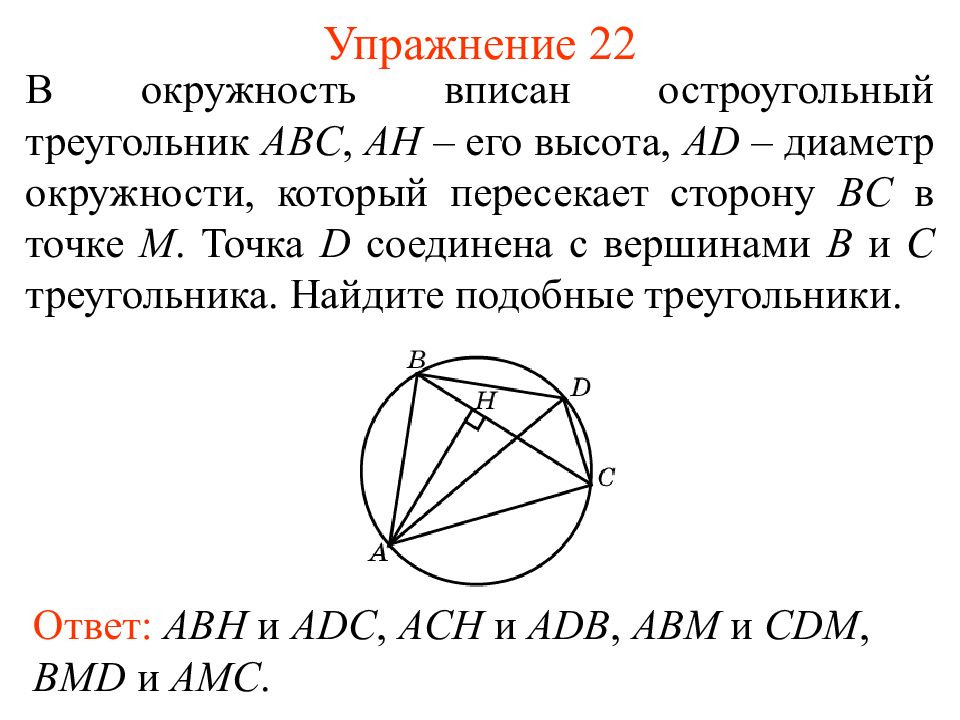
Слайд 27: Упражнение 22
Ответ: ABH и ADC, ACH и ADB, ABM и CDM, BMD и AMC. В окружность вписан остроугольный треугольник ABC, AH – его высота, AD – диаметр окружности, который пересекает сторону BC в точке M. Точка D соединена с вершинами B и C треугольника. Найдите подобные треугольники.
Слайд 28: Упражнение 23
Докажите, что произведение отрезков любой хорды, проведенной через внутреннюю точку круга, равно произведению отрезков диаметра, проведенного через ту же точку. Решение. Пусть дан круг с центром в точке O, хорда AB и диаметр CD пересекаются в точке E. Докажем, что Треугольники ACE и DBE подобны. Следовательно, значит,
Слайд 29: Упражнение 24
Через внешнюю точку E окружности проведены две прямые, пересекающая окружность соответственно в точках A, C и B, D. Докажите, что треугольники ADE и BCE подобны. Доказательство: Угол D треугольника ADE равен углу C треугольника BCE, как вписанные углы, опирающиеся на одну дугу окружности. Угол E этих треугольников общий. Следовательно, треугольники ADE и BCE подобны по первому признаку.
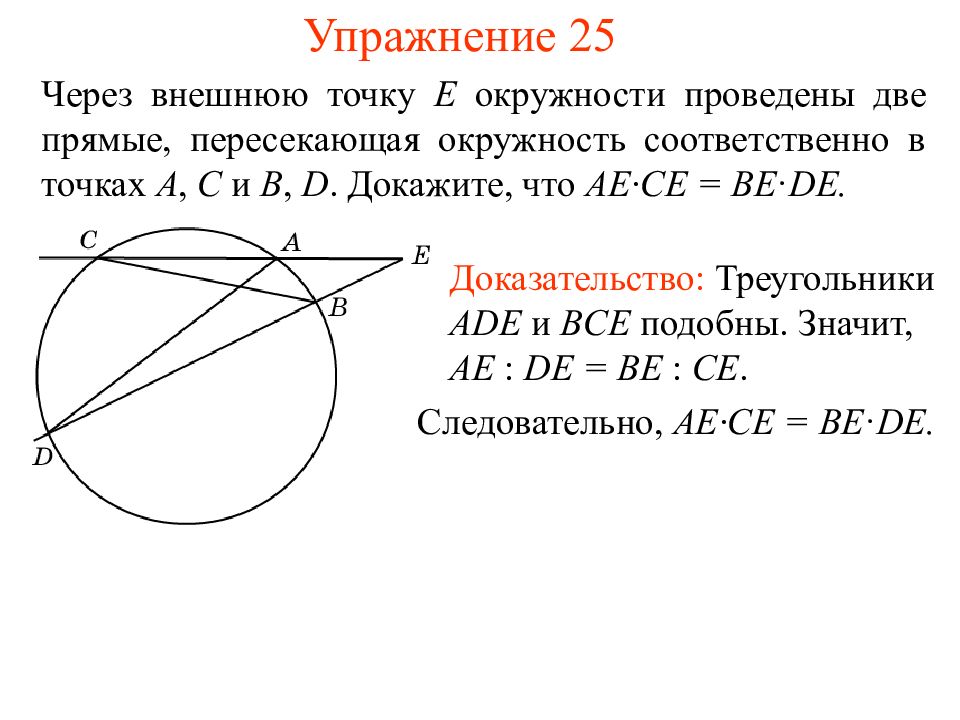
Слайд 30: Упражнение 2 5
Через внешнюю точку E окружности проведены две прямые, пересекающая окружность соответственно в точках A, C и B, D. Докажите, что AE ·CE = BE · DE. Доказательство: Треугольники ADE и BCE подобны. Значит, AE : DE = BE : CE. Следовательно, AE ·CE = BE · DE.
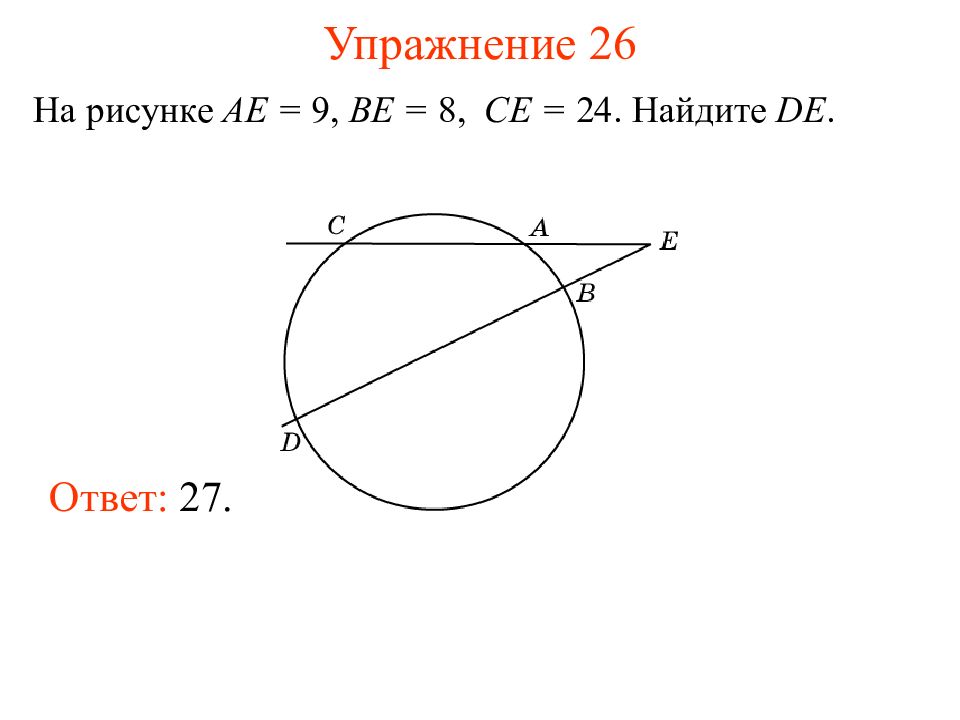
Слайд 31: Упражнение 2 6
На рисунке AE = 9, BE = 8, CE = 2 4. Найдите DE. Ответ: 27.
Слайд 32: Упражнение 27
Через внешнюю точку E окружности проведены прямая, пересекающая окружность в точках A и B, и касательная E С ( C – точка касания). Докажите, что треугольники EAC и ECB подобны. Доказательство. У треугольников EAC и ECB угол E общий. Углы ACE и CBE равны, как углы, опирающиеся на одну хорду. Следовательно, треугольники EAC и ECB подобны.
Слайд 33: Упражнение 28
Через внешнюю точку E окружности проведены прямая, пересекающая окружность в точках A и B, и касательная E С ( C – точка касания). Докажите, что произведение отрезков AE и BE секущей равно квадрату отрезка CE касательной. Доказательство. Треугольники EAC и ECB подобны. Следовательно, AE : CE = CE : BE, значит, AE ·BE = CE 2.
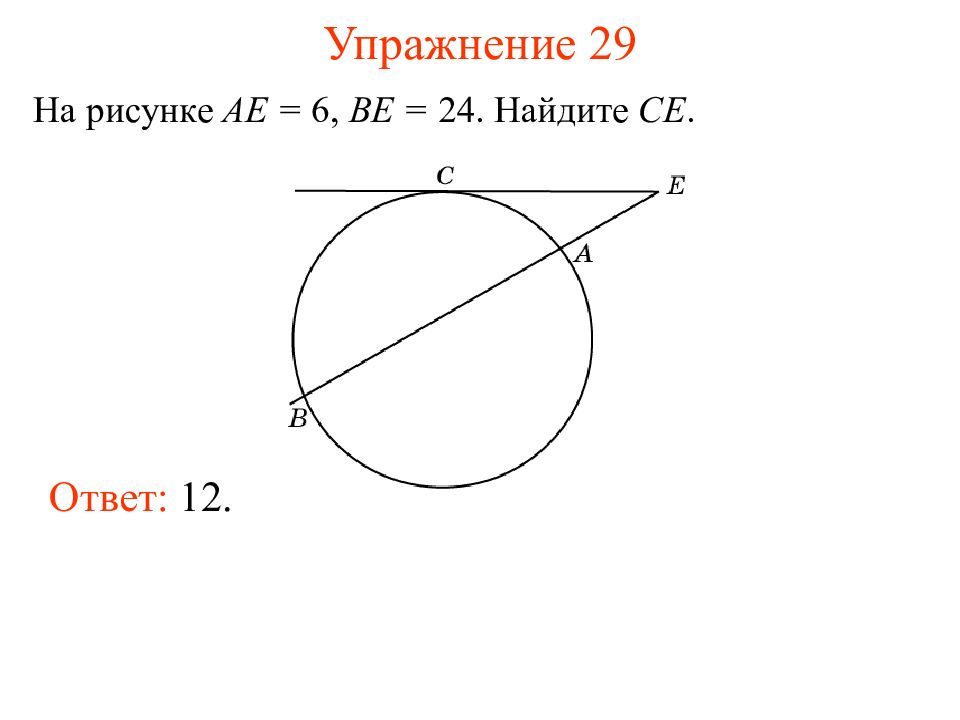
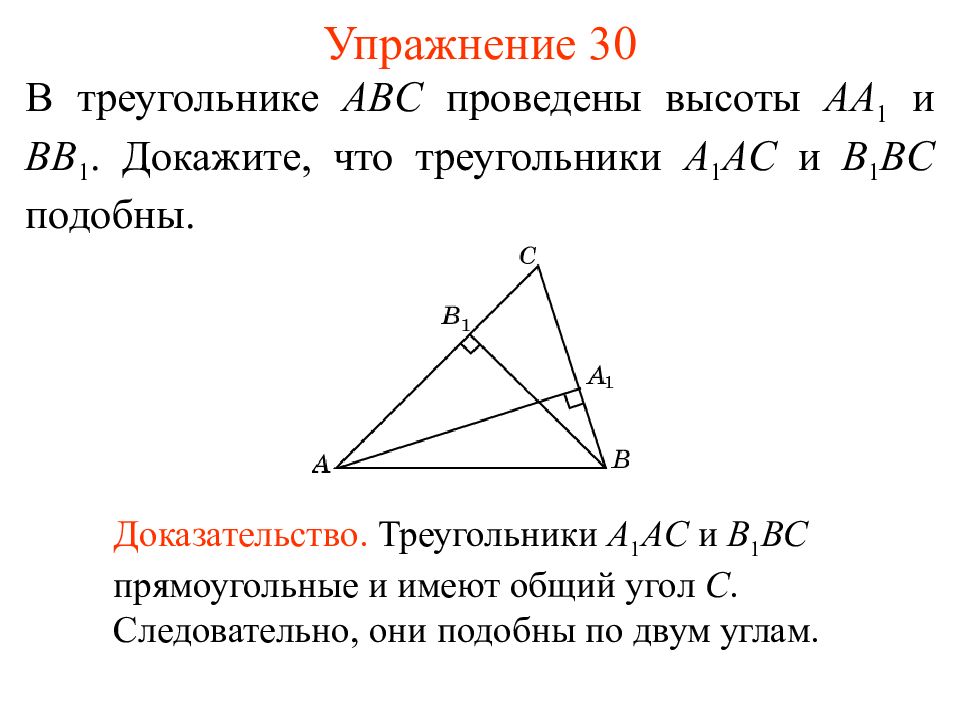
Слайд 35: Упражнение 30
В треугольнике ABC проведены высоты AA 1 и BB 1. Докажите, что треугольники A 1 AC и B 1 BC подобны. Доказательство. Треугольники A 1 AC и B 1 BC прямоугольные и имеют общий угол C. Следовательно, они подобны по двум углам.
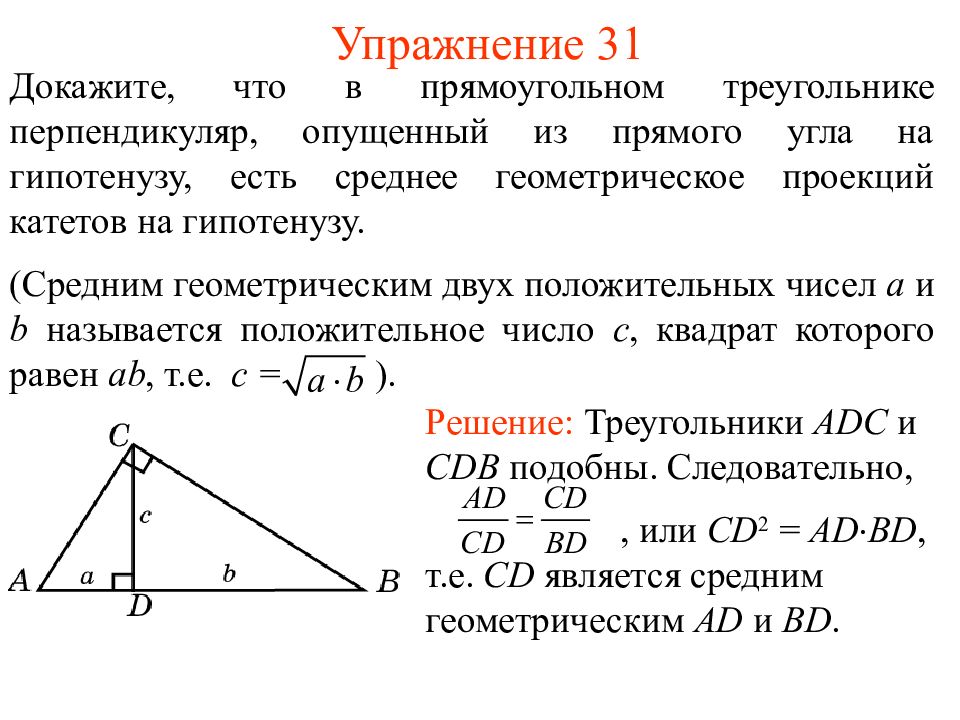
Слайд 36: Упражнение 3 1
Докажите, что в прямоугольном треугольнике перпендикуляр, опущенный из прямого угла на гипотенузу, есть среднее геометрическое проекций катетов на гипотенузу. ( С редним геометрическим двух положительных чисел a и b называется положительное число c, квадрат которого равен ab, т.е. c = ). Решение: Треугольники ADC и CDB подобны. Следовательно, , или CD 2 = AD BD, т.е. CD является средним геометрическим AD и BD.
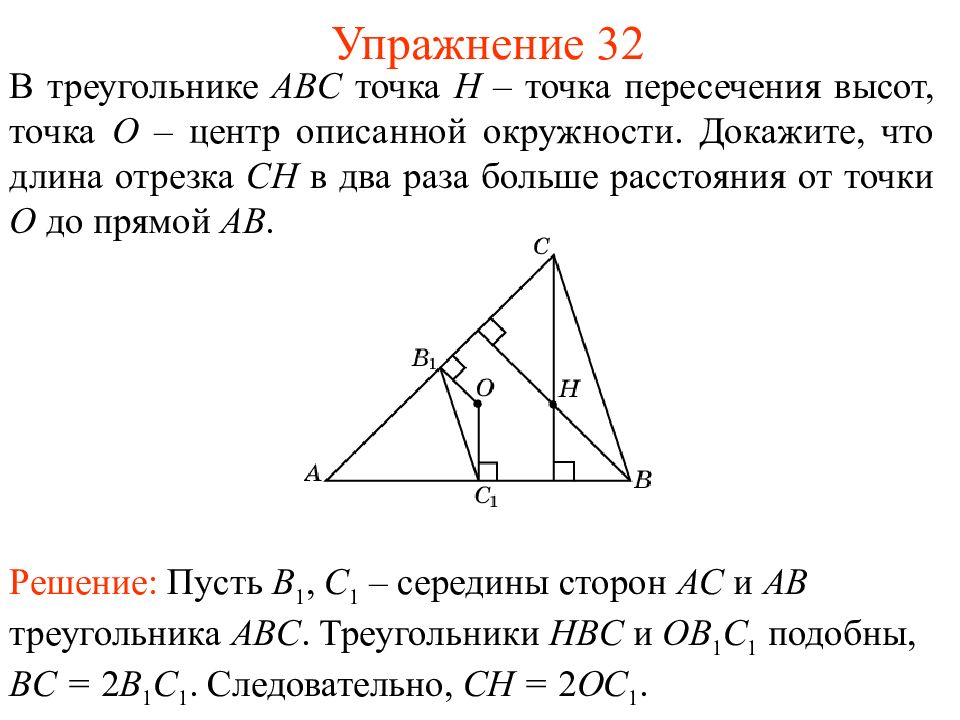
Последний слайд презентации: Подобие треугольников: Упражнение 32
В треугольнике ABC точка H – точка пересечения высот, точка O – центр описанной окружности. Докажите, что длина отрезка CH в два раза больше расстояния от точки O до прямой AB. Решение: Пусть B 1, C 1 – середины сторон AC и AB треугольника ABC. Треугольники HBC и OB 1 C 1 подобны, BC = 2 B 1 C 1. Следовательно, CH = 2 OC 1.