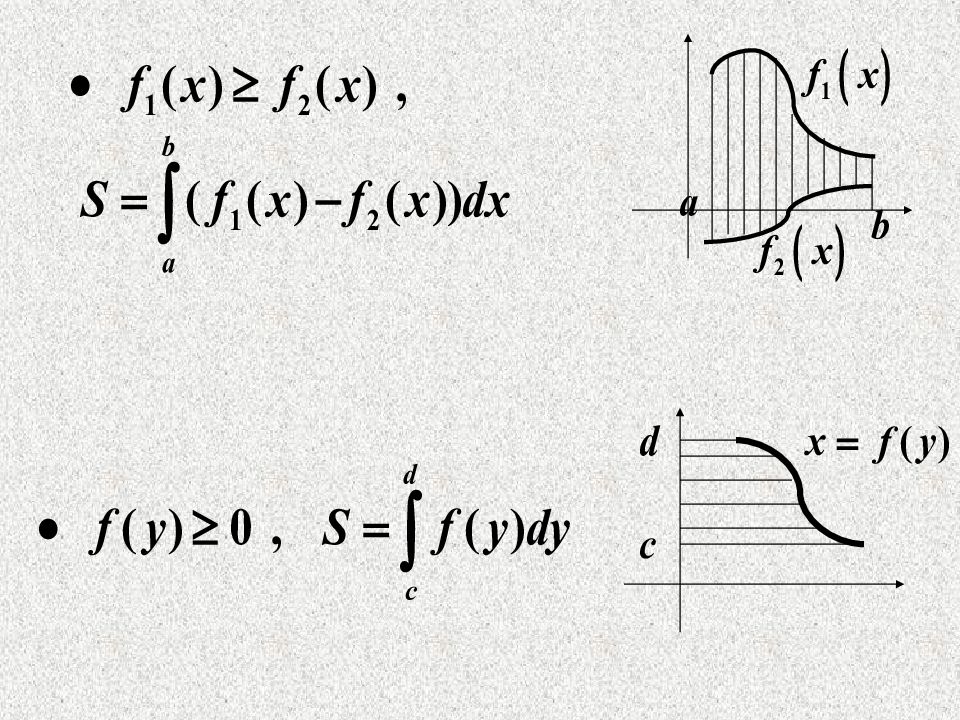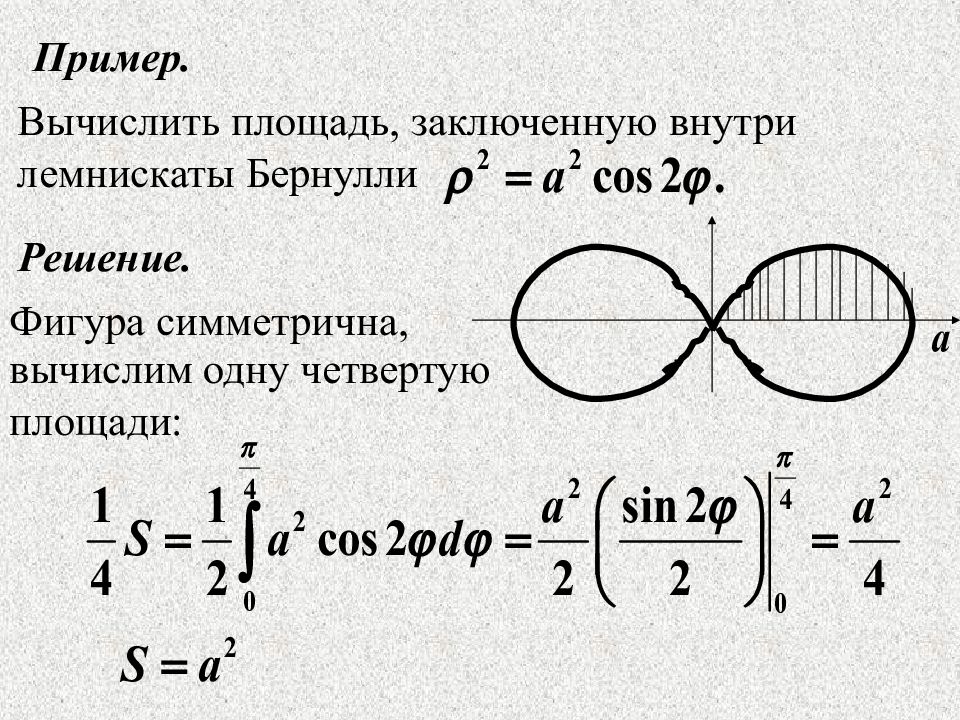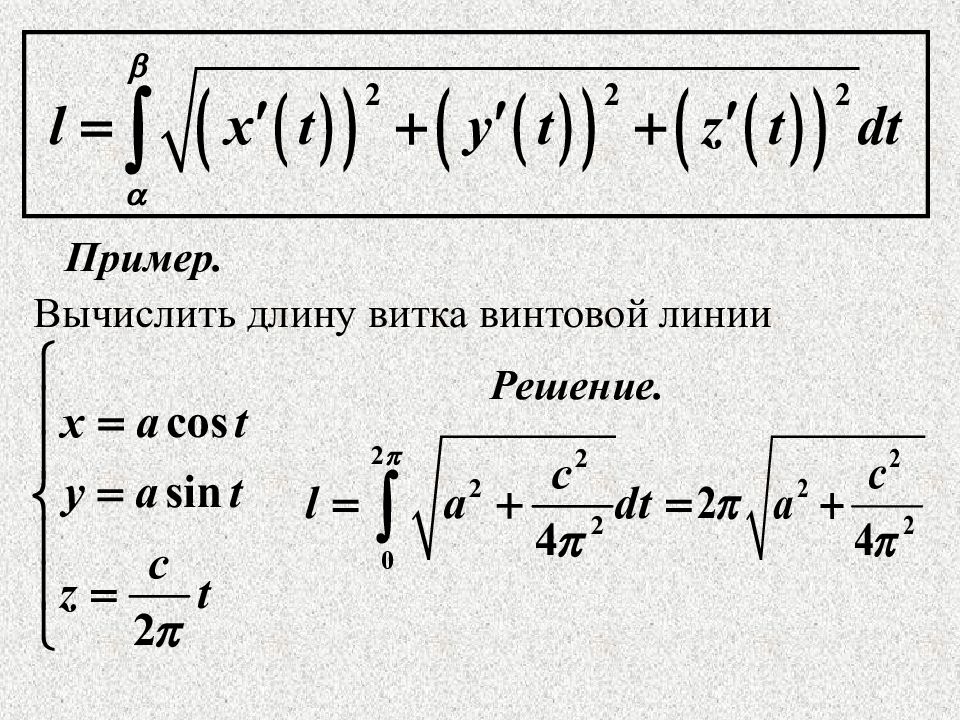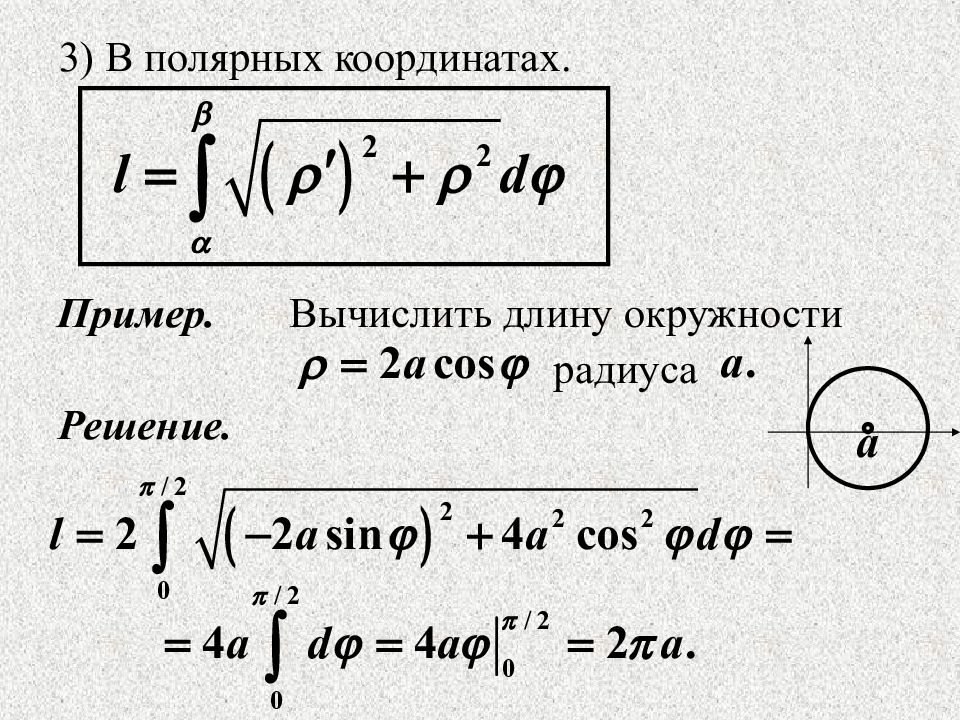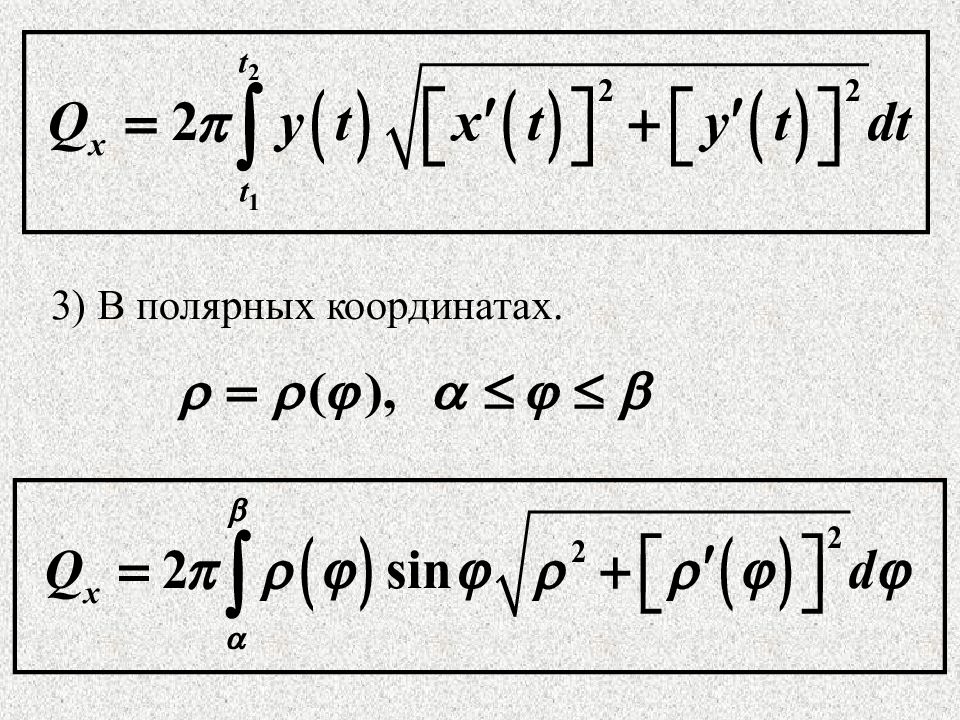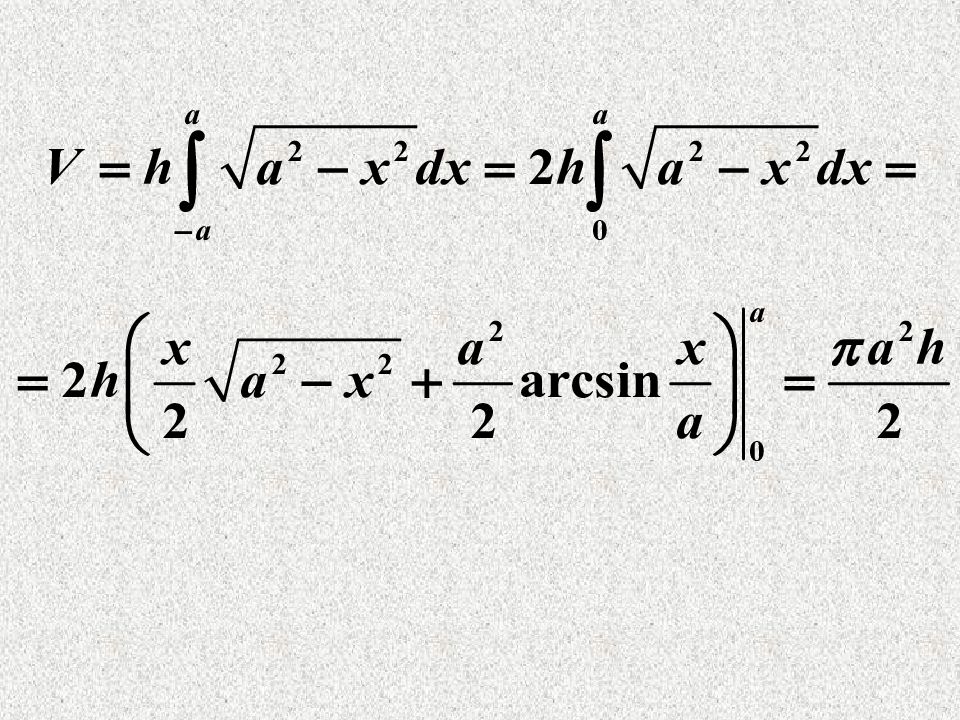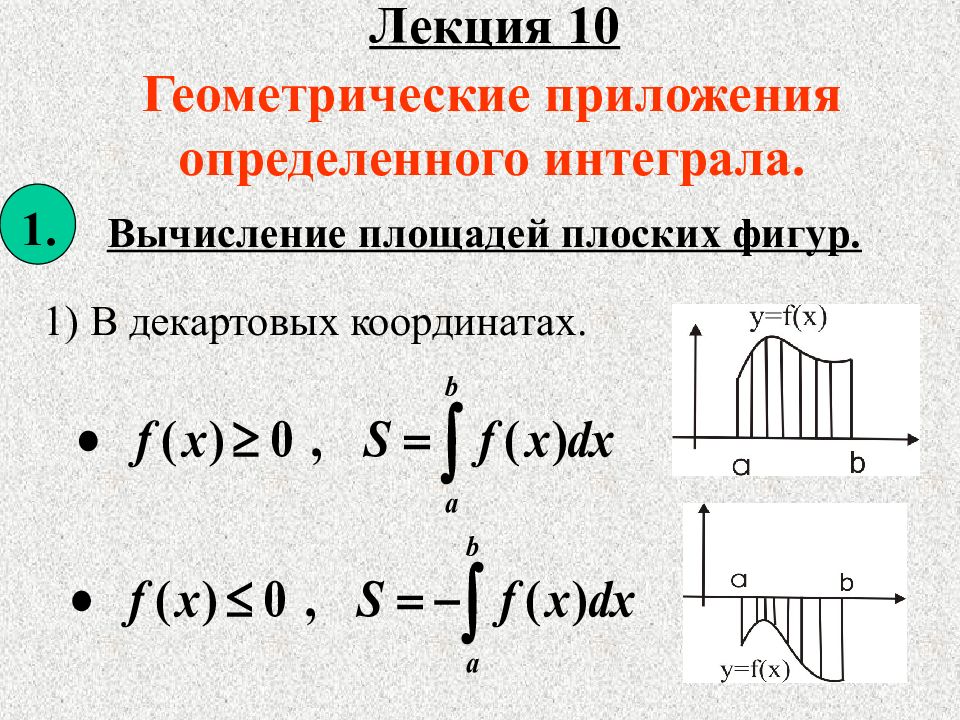
Лекция 10 Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур. 1. 1) В декартовых координатах.
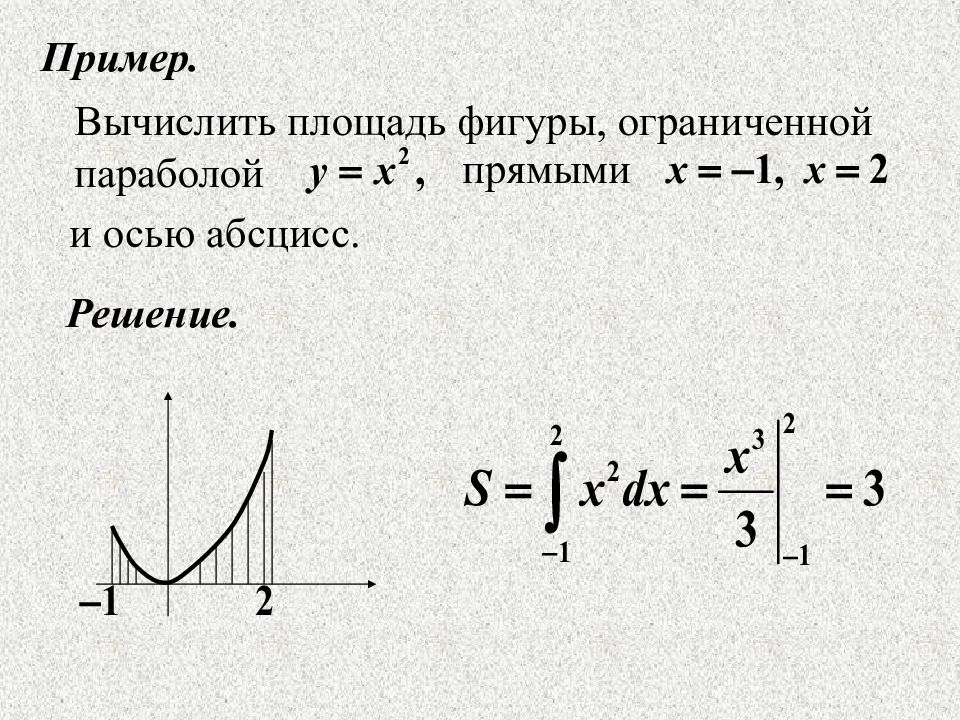
Вычислить площадь фигуры, ограниченной параболой прямыми и осью абсцисс. Пример. Решение.
2) В параметрической форме.
Вычислить площадь эллипса. Пример. Решение. Уравнения эллипса в параметрической форме:
3 ) В полярных координатах. и лучами Площадь криволинейного сектора, ограниченного кривой
Вычислить площадь, заключенную внутри лемнискаты Бернулли Пример. Решение. Фигура симметрична, вычислим одну четвертую площади :
Вычисление длины дуги кривой. 2. 1) В декартовых координатах. 2) В параметрической форме.
Пример. Вычислить длину витка винтовой линии Решение.
3 ) В полярных координатах. Пример. Вычислить длину окружности радиуса Решение.
Площадь поверхности, образованной вращением кривой вокруг оси О x Вычисление площади поверхности вращения. 3. 1) В декартовых координатах. 2) В параметрической форме.
3 ) В полярных координатах.
- площадь любого сечения тела плоскостью, перпендикулярной оси О x. Вычисление объёмов тел. 4. Вычисление объёмов по заданным площадям поперечных сечений. Объём тела
Пример. Найти объём тела, основание которого – круг радиуса, а сечение плоскостью, перпендикулярной любому диаметру круга - равнобедренный треугольник высотой Решение. Основание треугольника
2) Вычисление объёмов тел вращения. Если криволинейная трапеция, ограниченная кривой вращается вокруг оси О x, то объём тела вращения Здесь
Пример. Найти объём конуса с высотой и радиусом основания. Решение.
Несобственные интегралы. Если функция непрерывна на интервале ,то называется несобственным интегралом первого рода.
Если предел существует и конечен, то несобственный интеграл называется сходящимся. Точно также, для интервала Если предел не существует, или бесконечен, то несобственный интеграл называется расходящимся. Для интервала
Обобщённая формула Ньютона-Лейбница. Если - первообразная для функции на промежутке, то Точно также,
Вычислить несобственные интегралы, или доказать что они расходятся. (сходится) Пример. (расходится) (предел не существует, поэтому интеграл расходится)
Признаки сходимости интегралов с бесконечными пределами. Признаки сравнения 1. Пусть при Тогда, если сходится, то сходится и Если расходится, то расходится и
2. Если при то интегралы ведут себя одинаково в отношении сходимости и расходимости. и существует конечный предел
расходится и исходный интеграл. расходится Пример. Исследовать на сходимость Решение.
Несобственные интегралы второго рода. Если функция непрерывна на интервале и неограничена вблизи называется несобственным интегралом второго рода. кроме того то
непрерывной на и неограниченной вблизи точки : Точно также, для функции Если предел существует и конечен, то несобственный интеграл называется сходящимся. Если предел не существует, или бесконечен, то несобственный интеграл называется расходящимся.
Для функции непрерывной на отрезке всюду, кроме некоторой точки и неограниченной вблизи Если каждый из интегралов в правой части равенства сходится, то несобственный интеграл В противном случае – расходящимся. называется сходящимся.
Пример. Исследовать на сходимость Решение. несобственный интеграл сходится. Функция не ограничена при По обобщенной формуле Ньютона-Лейбница:
Признаки сходимости несобственных интегралов от неограниченных функций такие же, как и признаки сходимости интегралов с бесконечными пределами.
