ЛЕКЦИЯ 3 ЗУБЧАТЫЕ ПЕРЕДАЧИ
Зубчатая передача - трехзвенный механизм, включающий два подвижных звена, взаимодействующих между собой через высшую зубчатую кинематическую пару и образующих с третьим неподвижным звеном низшие (вращательные или поступательные) кинематические пары.
Зубчатые передачи являются средствами передачи крутящего момента и определяют скорость вращения машинных валов. Они могут изменять направление оси вращения и менять вращательное движение на линейное движение
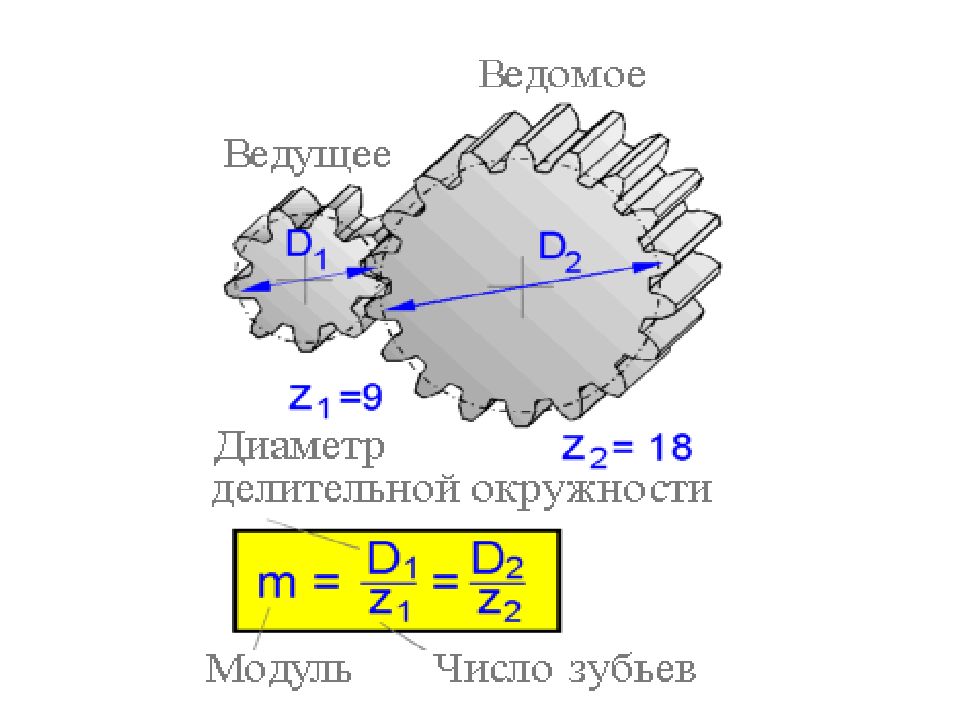
Меньшее зубчатое колесо, участвующее в зацеплении обычно называют шестерней, большее – зубчатым колесом, звено зубчатой передачи, совершающее прямолинейное движение, называют зубчатой рейкой
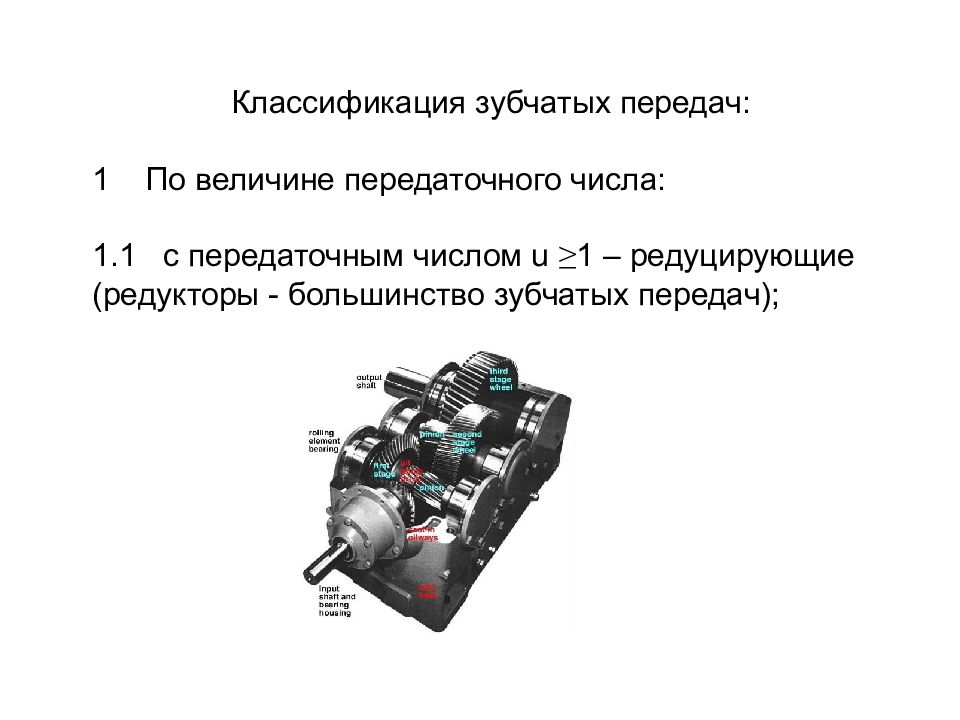
Классификация зубчатых передач: 1 По величине передаточного числа: 1.1 с передаточным числом u ≥ 1 – редуцирующие (редукторы - большинство зубчатых передач);
Обычно редуктором называют устройство, преобразующее высокую угловую скорость вращения входного вала в более низкую на выходном валу, повышая при этом вращающий момент, такой редуктор обычно называют демультипликатором, а редуктор, который преобразует низкую угловую скорость в более высокую обычно называют мультипликатором.
1.2 с передаточным числом u < 1 – мультиплицирующие (мультипликаторы).
2. По взаимному расположению валов: 2.1 с параллельными валами
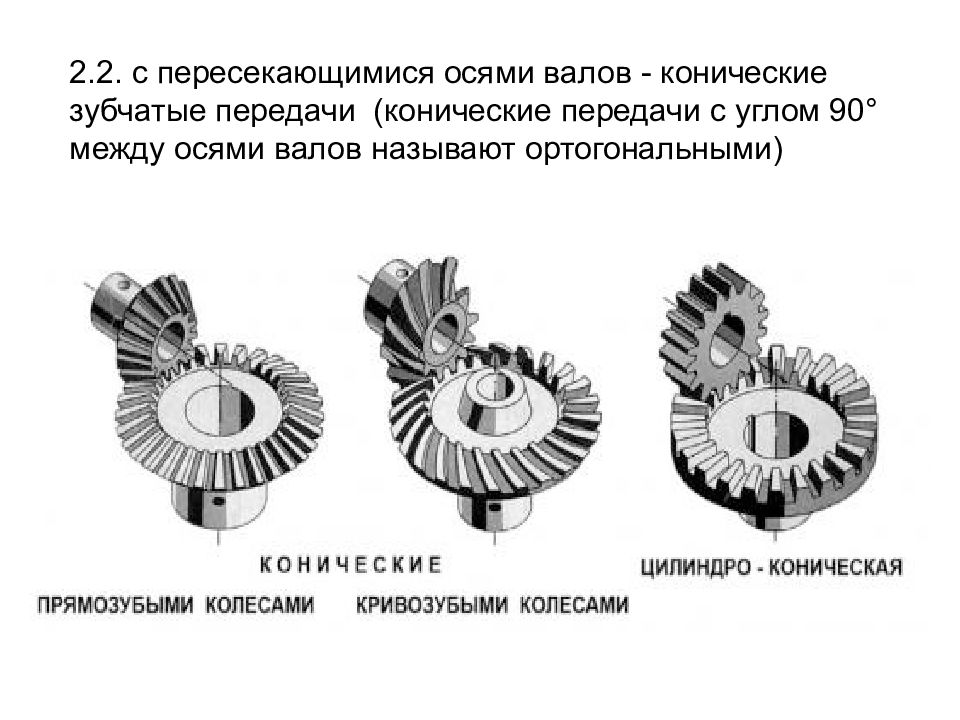
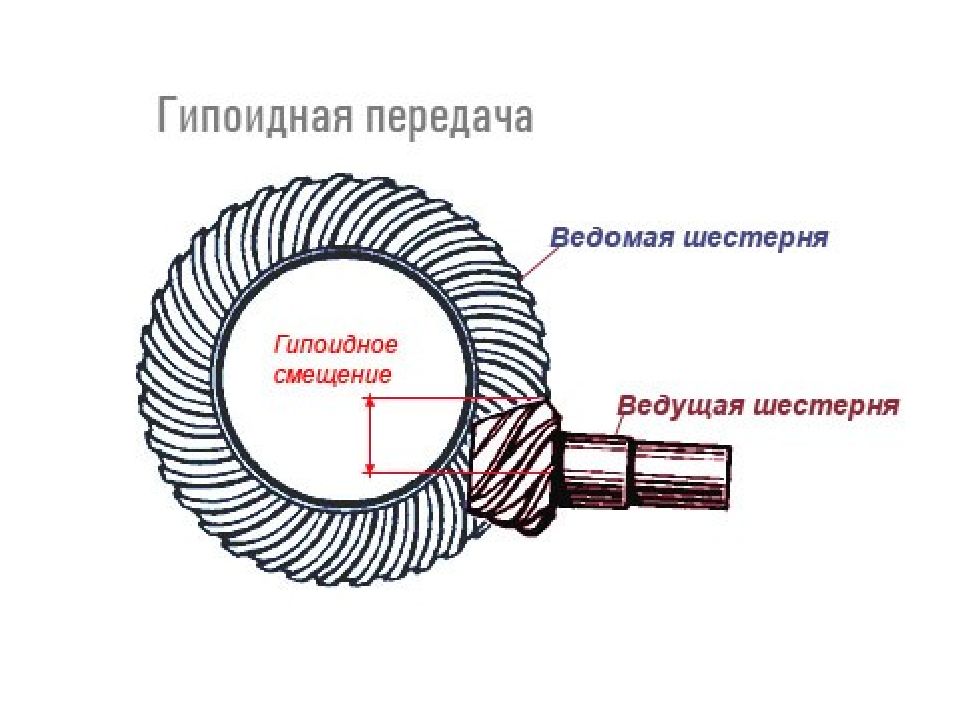
2.2. с пересекающимися осями валов - конические зубчатые передачи (конические передачи с углом 90° между осями валов называют ортогональными)
2.3 с перекрещивающимися осями валов - червячные, винтовые, гипоидные
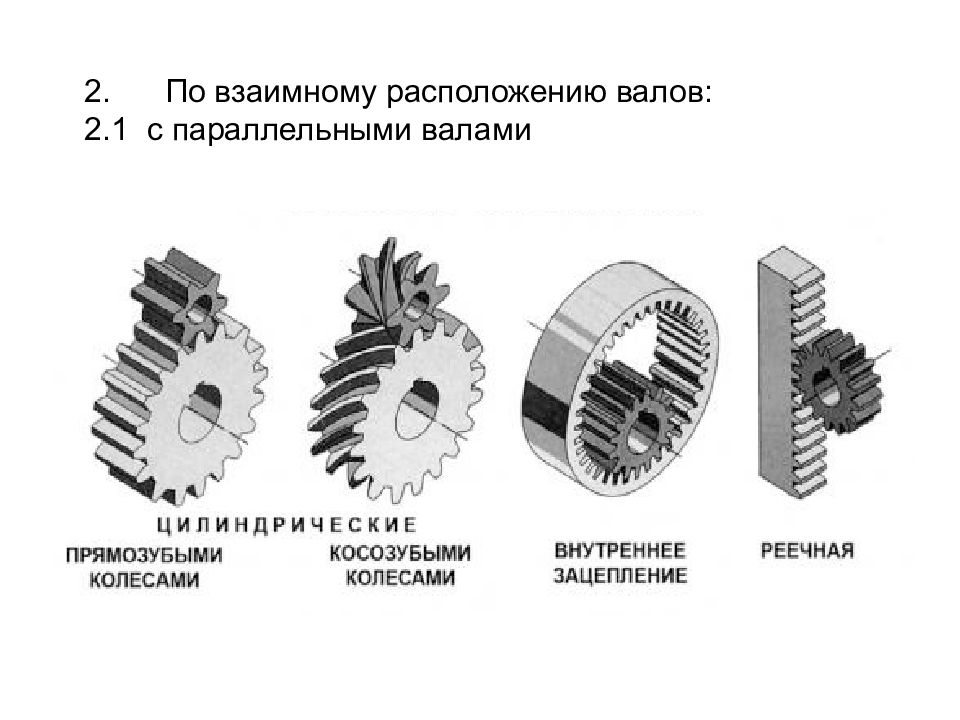
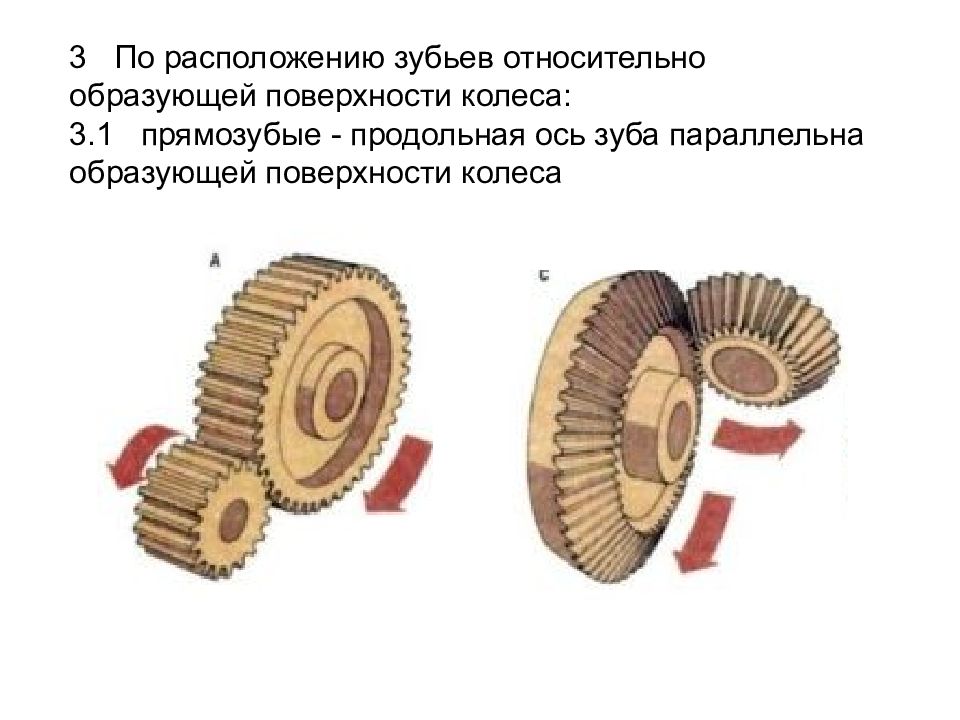
3 По расположению зубьев относительно образующей поверхности колеса: 3.1 прямозубые - продольная ось зуба параллельна образующей поверхности колеса
3.2 косозубые - продольная ось зуба направлена под углом к образующей поверхности колеса
3.3 шевронные - зуб выполнен в форме двух косозубых колес со встречным наклоном осей зубьев
3.4 с круговым зубом (тангенциальные) - ось зуба выполнена по окружности относительно образующей поверхности колеса
4 По форме зацепляющихся звеньев:
4.1 с внешним зацеплением - зубья направлены своими вершинами от оси вращения колеса
4.2 с внутренним зацеплением - зубья одного из зацепляющихся колес направлены своими вершинами к оси вращения колеса
4.3 реечное зацепление - одно из колес заменено прямолинейной зубчатой рейкой
4.4 с некруглыми колесами.
С замкнутыми центроидами
С незамкнутыми центроидами
Многовитковым колесом
Передача без трения
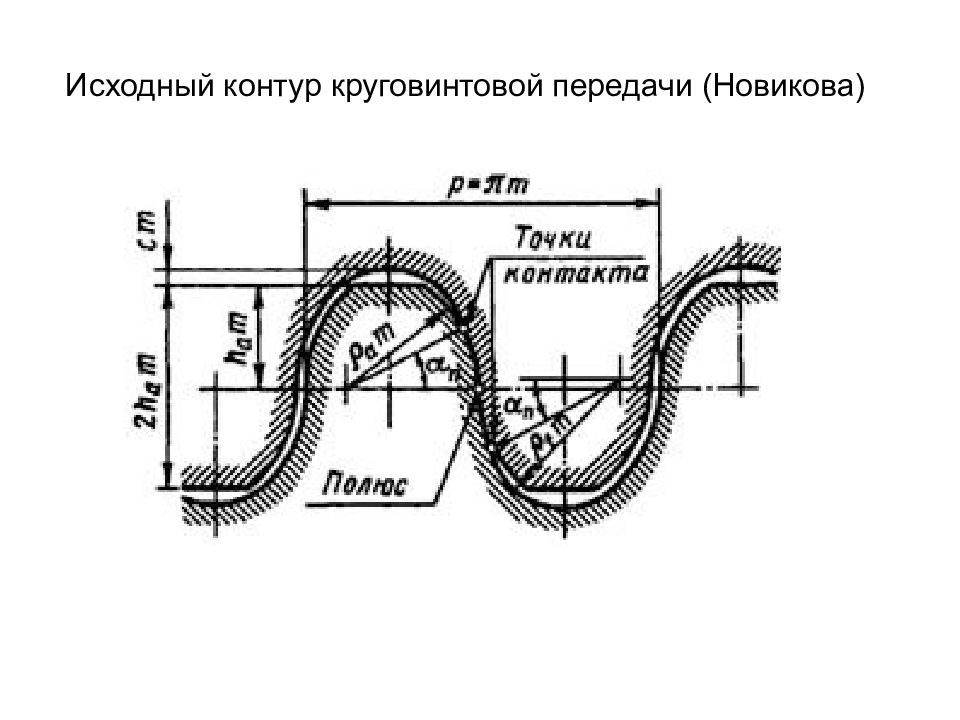
5 По форме рабочего профиля зуба: 5.1 эвольвентные - рабочий профиль зуба очерчен по эвольвенте круга (линия описываемая точкой прямой, катящейся без скольжения по окружности); 5.2 циклоидальные - рабочий профиль зуба очерчен по круговой циклоиде (линия описываемая точкой окружности, катящейся без скольжения по другой окружности); 5.3 цевочное (разновидность циклоидального) – зубья одного из колес, входящих в зацепление, заменены цилиндрическими пальцами – цевками; 5.4 с круговым профилем зуба (зацепление Новикова) – рабочие профили зубьев образованы дугами окружности практически одинаковых радиусов.
Эвольвентное зацепление, предложенное Леонардом Эйлером (в 1760 или 65 г.), которое и получило самое широкое распространение в общепромышленной и военной технике.
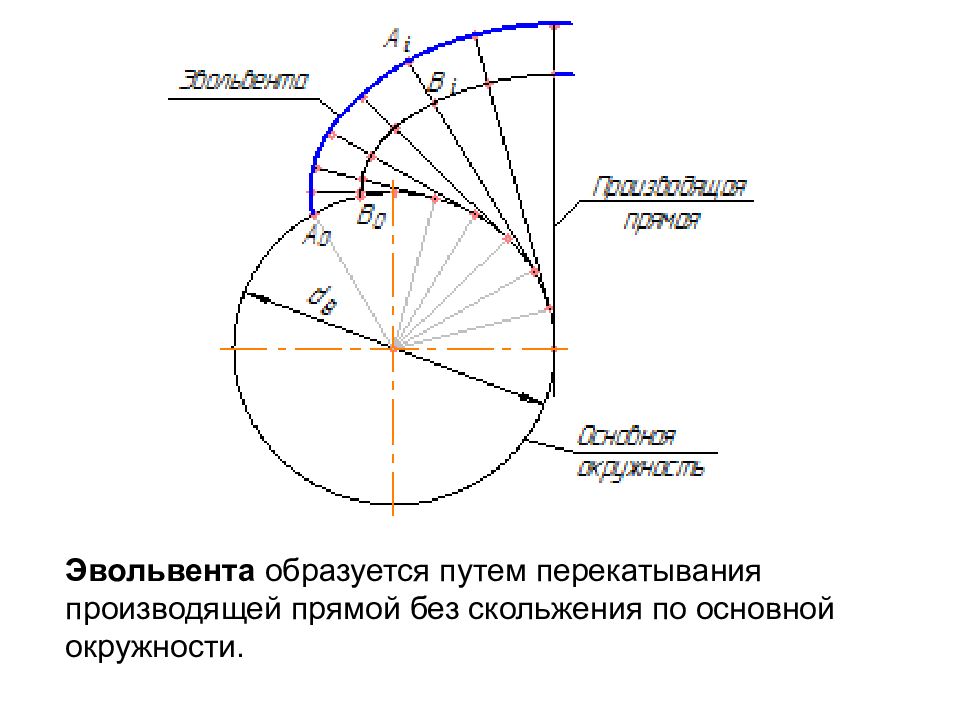
Эвольвента образуется путем перекатывания производящей прямой без скольжения по основной окружности.
Циклоидальные и цевочные зацепления были известны примерно на 100 лет раньше эвольвентных. Циклоидальное зацепление – это зацепление, в котором боковые рабочие поверхности зубьев сопряженных колес очерчены по циклоиде. Циклоида - кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности. При обкатывании производящей окружности по главной окружности с внешней стороны получаем эпициклоиду, а при обкатывании с внутренней стороны – гипоциклоиду. При этом производящая окружность обкатывается по делительной окружности зубчатого колеса, совпадающей в зацеплении с начальной окружностью.
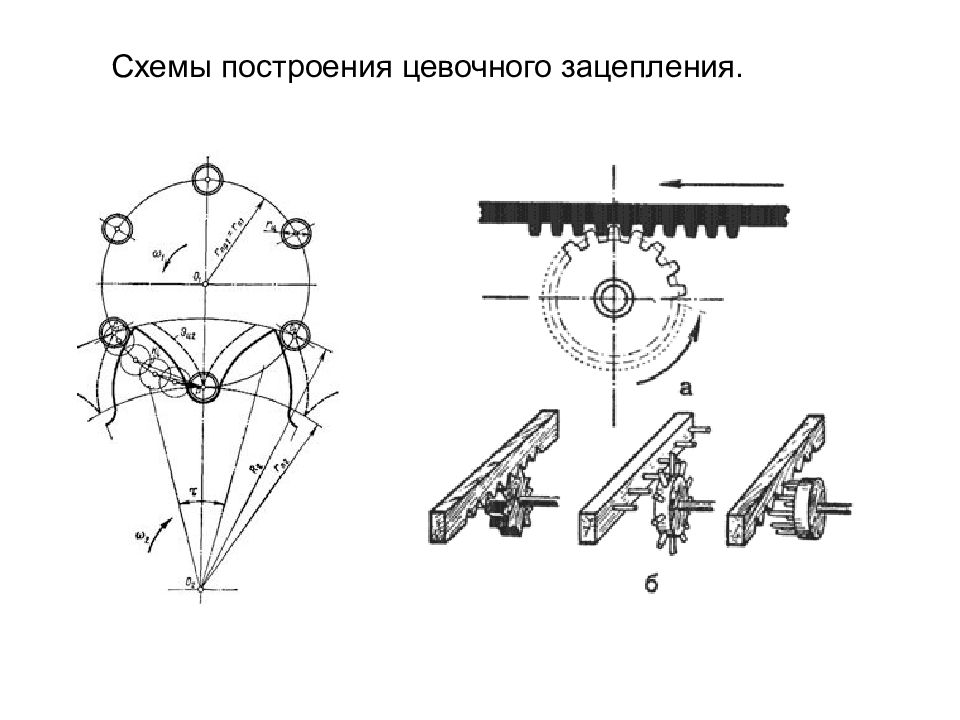
Цевочное зацепление применяется в зубчатых механизмах больших габаритов: в подъемно-транспортных механизмах, в механизмах поворота орудийных башен, в некоторых типах планетарных редукторов. Во всех этих механизмах цевочным выполняют большее колесо, что позволяет отказаться от крупногабаритных зубофрезерных станков. Частным случаем циклоидального зацепления является цевочное зацепление. Цевочное зацепление может быть как внешним, так и внутренним.
Схемы построения цевочного зацепления.
а - шестерня с одним зубом, б - мальтийский крест Ведущие шестерни встречаются и с одним зубцом. Такие передачи очень часто применялись в счетных механизмах. Ведущая шестерня имеет один зубец, а ведомая - десять, и, таким образом, за один оборот ведущей шестерни ведомая повернется всего на одну десятую оборота.
Исходный контур круговинтовой передачи (Новикова)
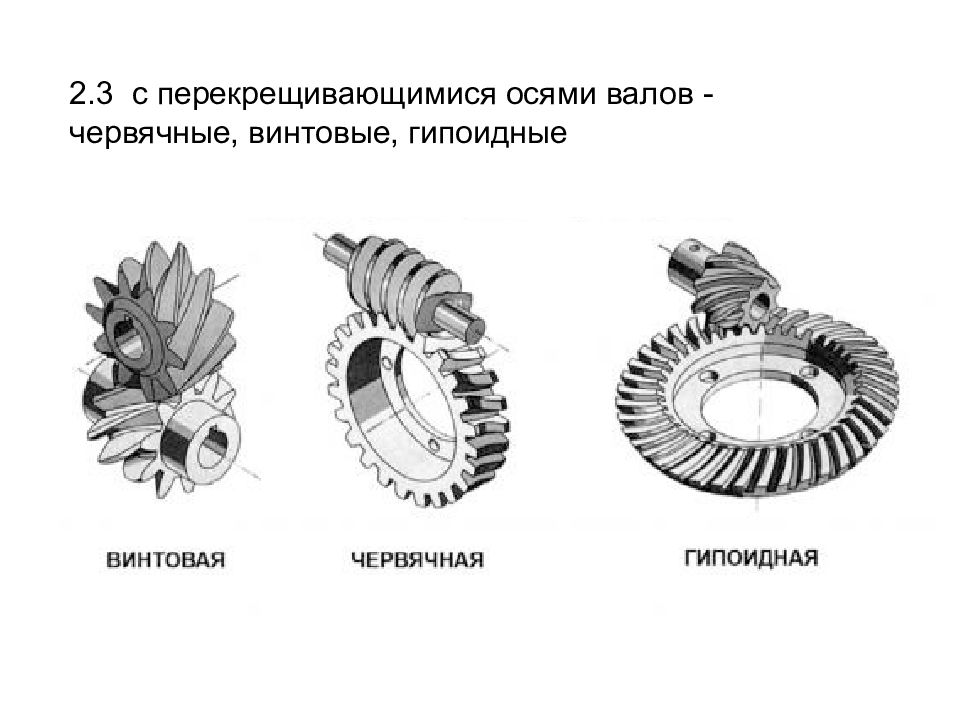
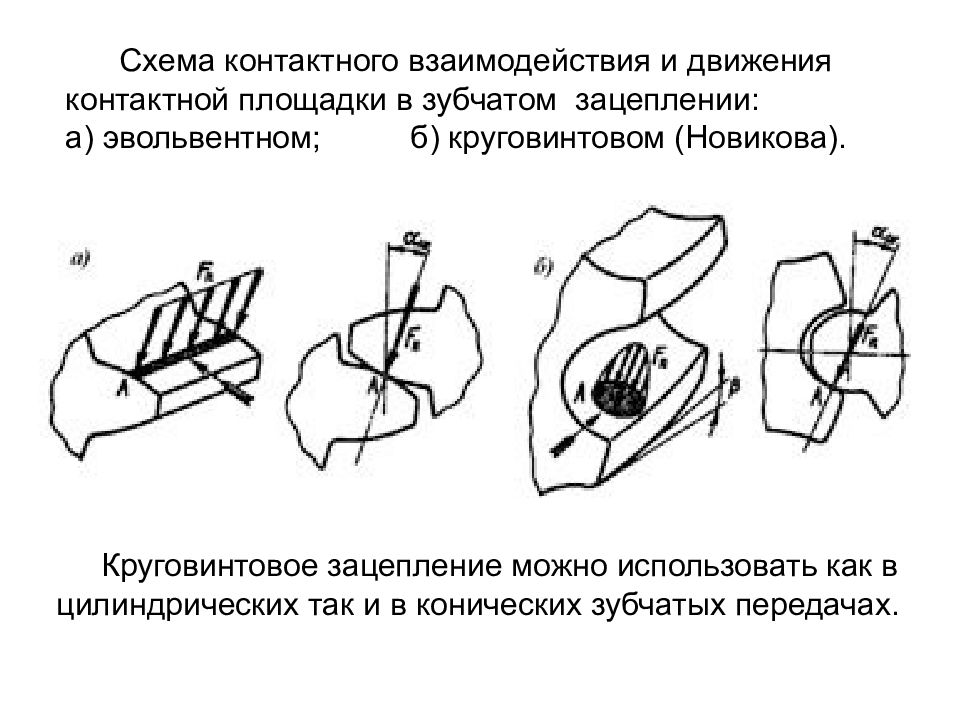
Схема контактного взаимодействия и движения контактной площадки в зубчатом зацеплении: а) эвольвентном; б) круговинтовом (Новикова). Круговинтовое зацепление можно использовать как в цилиндрических так и в конических зубчатых передачах.
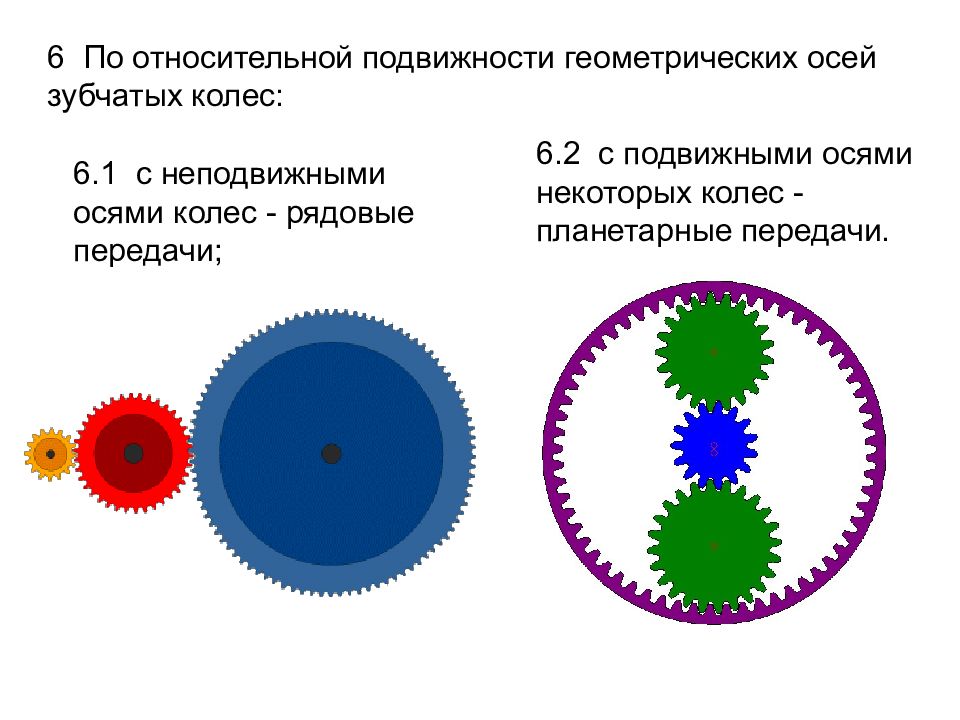
6 По относительной подвижности геометрических осей зубчатых колес: 6.2 с подвижными осями некоторых колес - планетарные передачи. 6.1 с неподвижными осями колес - рядовые передачи;
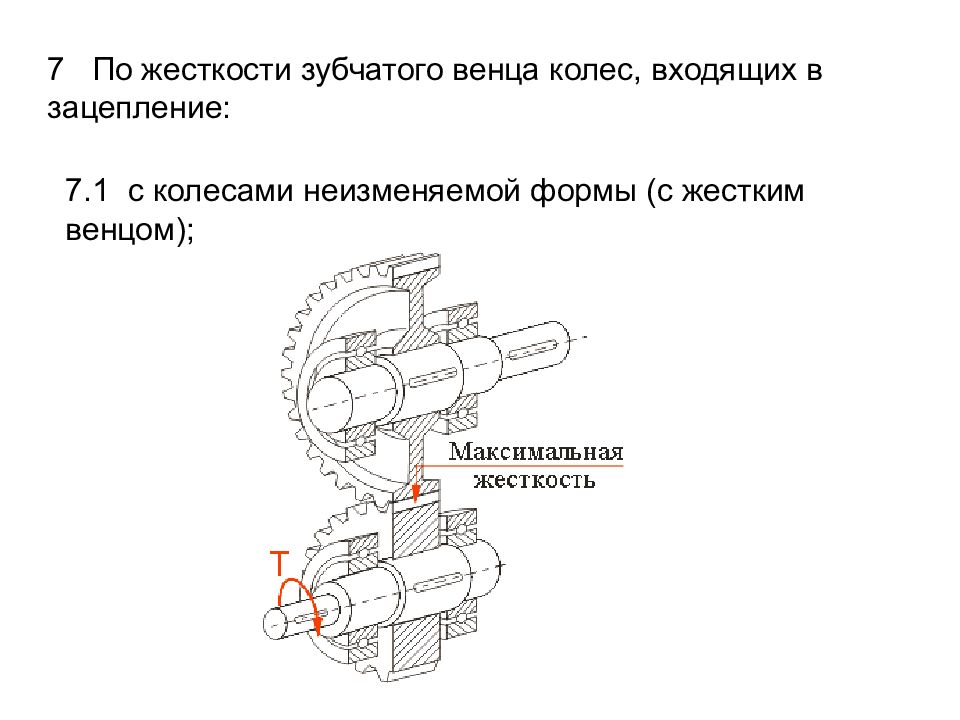
7 По жесткости зубчатого венца колес, входящих в зацепление: 7.1 с колесами неизменяемой формы (с жестким венцом);
7.2 колеса с венцом изменяющейся формы (гибким).
8. По окружной (тангенциальной) скорости зубьев: 8.1. тихоходные (Vокр < 3 м/с); 8.2. среднескоростные (3< Vокр < 15 м/с); 8.3. быстроходные (Vокр > 15 м/с). 9. По конструктивному исполнению: 9.1. открытые (бескорпусные); 9.2. закрытые (корпусные).
Достоинства зубчатых передач: Высокая надежность работы в широком диапазоне нагрузок и скоростей. Большой ресурс. Малые габариты. Высокий КПД. Относительно малые нагрузки на валы и подшипники. Постоянство передаточного числа. Простота обслуживания.
Недостатки зубчатых передач: Сложность изготовления и ремонта (необходимо высокоточное специализированное оборудование). Относительно высокий уровень шума, особенно на больших скоростях. Нерациональное использование зубьев – в работе передачи одновременно участвуют обычно не более двух зубьев каждого из зацепляющихся колёс.
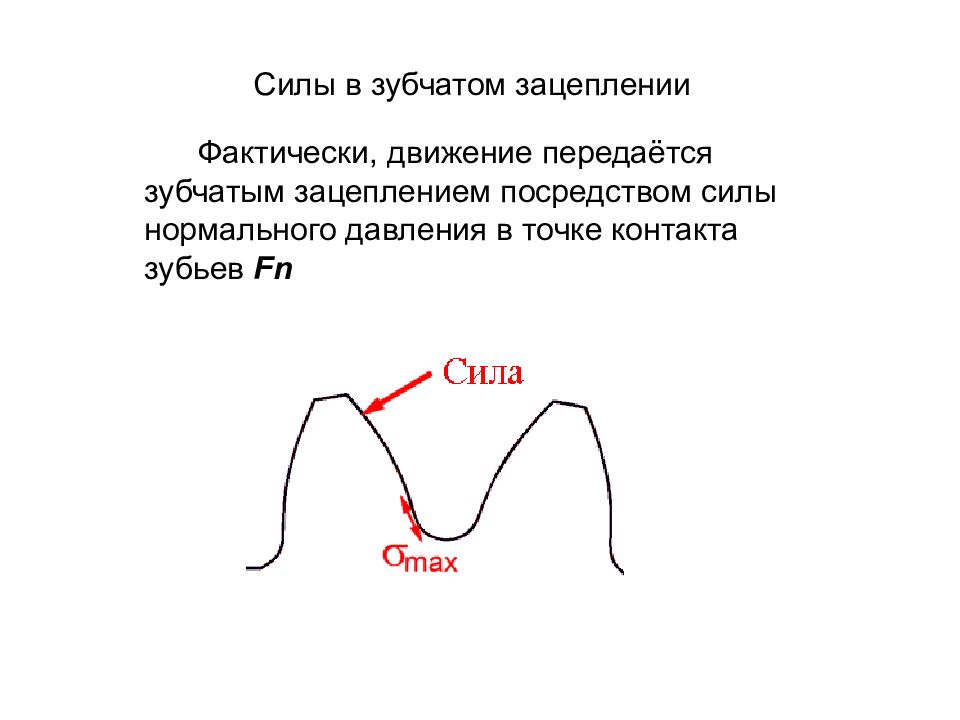
Силы в зубчатом зацеплении Фактически, движение передаётся зубчатым зацеплением посредством силы нормального давления в точке контакта зубьев Fn
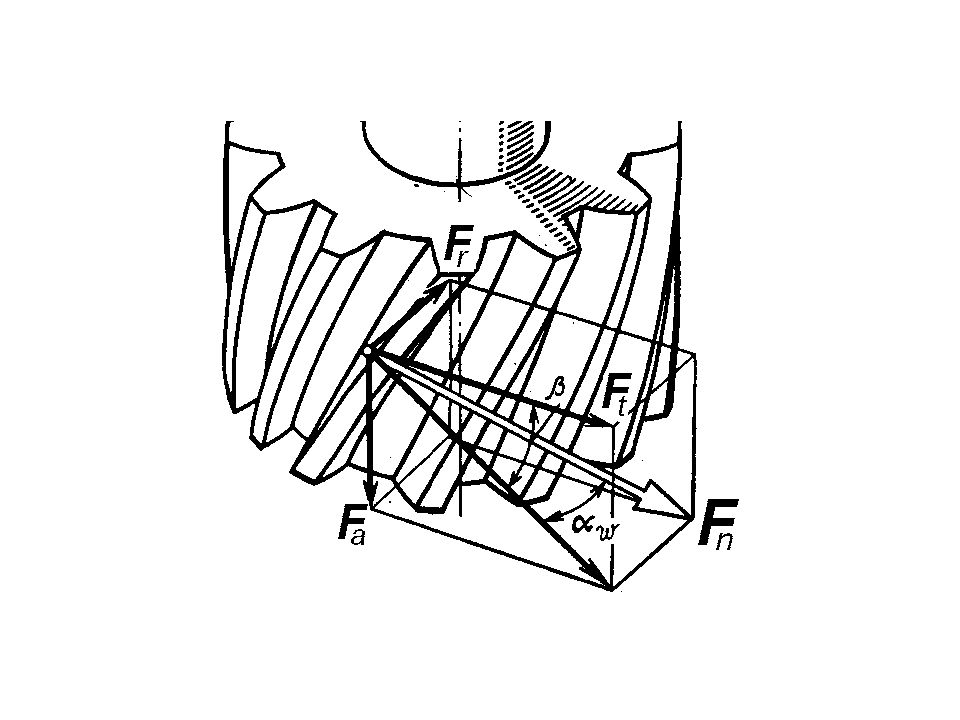
сначала раскладывают на три ортогональных проекции: - осевую силу Fa, направленную параллельно оси колеса; - радиальную силу Fr, направленную по радиусу к центру колеса; - окружную силу Ft, направленную касательно к делительной окружности.
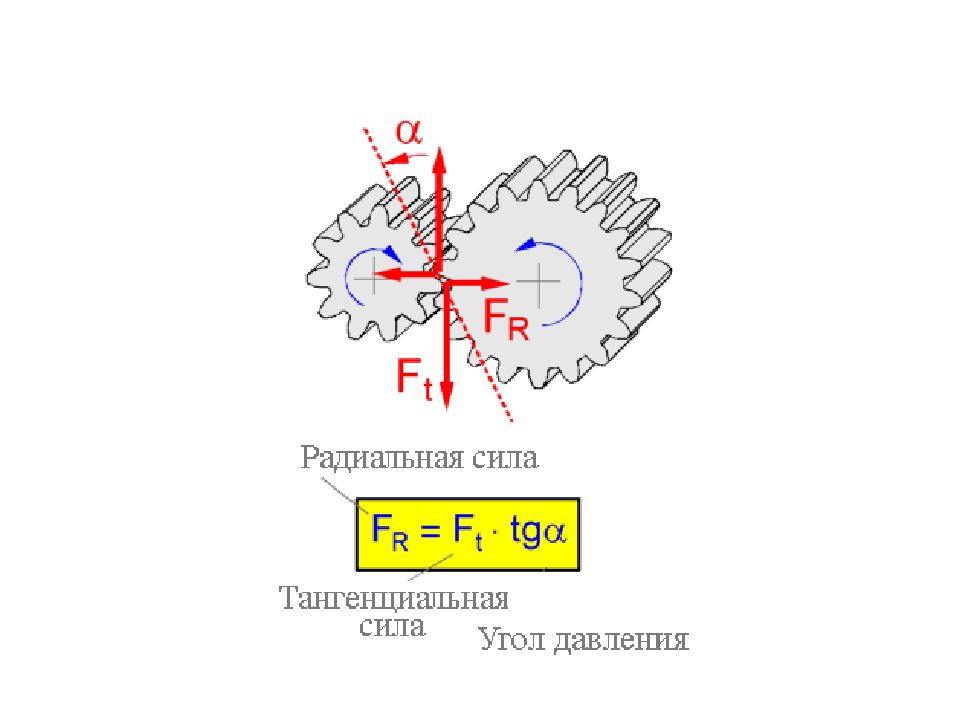
Легче всего вычислить силу Ft, зная передаваемый вращающий момент Мвр (Т) и делительный диаметр dw Ft = 2M вр / dw. Радиальная сила вычисляется, зная угол зацепления α w Fr = Ft tg α w. Осевая сила вычисляется через окружную силу и угол наклона зубьев β Fa = Ft tg β.
РАСЧЕТ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ ПЕРЕДАЧ НА ПРОЧНОСТЬ ПО КОНТАКТНЫМ НАПРЯЖЕНИЯМ И НА ИЗГИБ
Расчет цилиндрической зубчатой передачи 1. Межосевое расстояние Величину округляют до стандартного значения
- коэффициент ширины зубчатого венца коэффициент концентрации нагрузки при расчете на контактную выносливость К а - коэффициент межосевого расстояния К а = 490 МПа 1/3 для стальных прямозубых колес K a = 430 МПа 1/3 для стальных косозубых колес. Т 2 - крутящий момент на выходном валу - допускаемое контактное напряжение
2. Ширина зубчатого венца колеса , , ; величину в округляют до ближайшего нормального линейного размера шестерни
3. Окружной модуль зубьев колес m n где где - коэффициент ширины зубчатого венца относительно модуля. Величина m n округляется до ближайшего стандартного значения
4. Угол наклона зубьев косозубых передач определяется по формуле или по таблице где - коэффициент осевого перекрытия, . 5. Суммарное число зубьев Z c
6. Число зубьев ведущего колеса Z 1 7. Число зубьев ведомого колеса Z 2 8. Фактическое передаточное число U. Фактическое передаточное число не должно отличаться от стандартного более чем на 2,5% при U ≤ 4,5 и на 4,0% при U > 4,5
9. Диаметр делительной окружности ведущего колеса 10. Диаметр делительной окружности ведомого колеса 11. Уточненное значение угла наклона зубьев 12. Окружная скорость в зацеплении
13. Контактные напряжения при расчете на выносливость Z M - коэффициент, учитывающий механические свойства материала зубчатых колес Z H - коэффициент, учитывающий форму сопряженных поверхностей зубьев - коэффициент, учитывающий длину контактной линии - удельная расчетная окружная сила
14. Напряжения изгиба при расчете на выносливость У F - коэффициент формы зуба считают по формуле или выбирают по графику - коэффициент, учитывающий угол наклона зуба - коэффициент, учитывающий многопарность зацепления - удельная расчетная окружная сила при расчете на изгиб
15. Максимальные контактные напряжения при перегрузке Где Т П - крутяший момент при кратковременных перегрузках, , К П - коэффициент перегрузки, Т max - максимальный крутящий момент при расчете на выносливость.
16. Максимальные напряжения изгиба при перегрузках
Виды разрушения зубьев
a. Разрушение ножки зуба от изгибной усталости. b. Усталостное выкрашивание. c. Поверхностное абразивное изнашивание. d. Образование задиров на поверхности из-за плохой смазки.
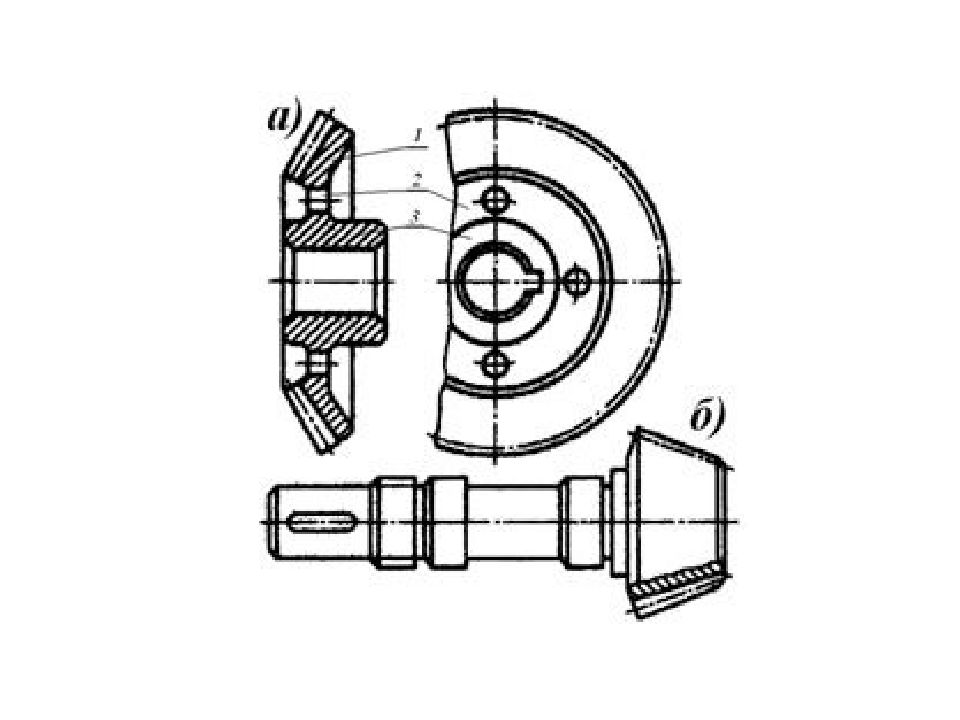
В единичном и мелкосерийном производстве зубчатые колеса диаметром до 200 мм обычно изготавливают методом точения из круглого проката. Заготовку для колес диаметром до 600 мм часто получают ковкой, а в массовом производстве горячей штамповкой в двусторонних молотовых штампах. Заготовки колес большего диаметра в мелкосерийном производстве изготавливают сваркой, а в массовом производстве для этой цели используют технологию литья в земляные формы.
Конструкции зубчатых колёс.
Элементы цилиндрических зубчатых колёс.
Конструктивные параметры точеных и кованых колес
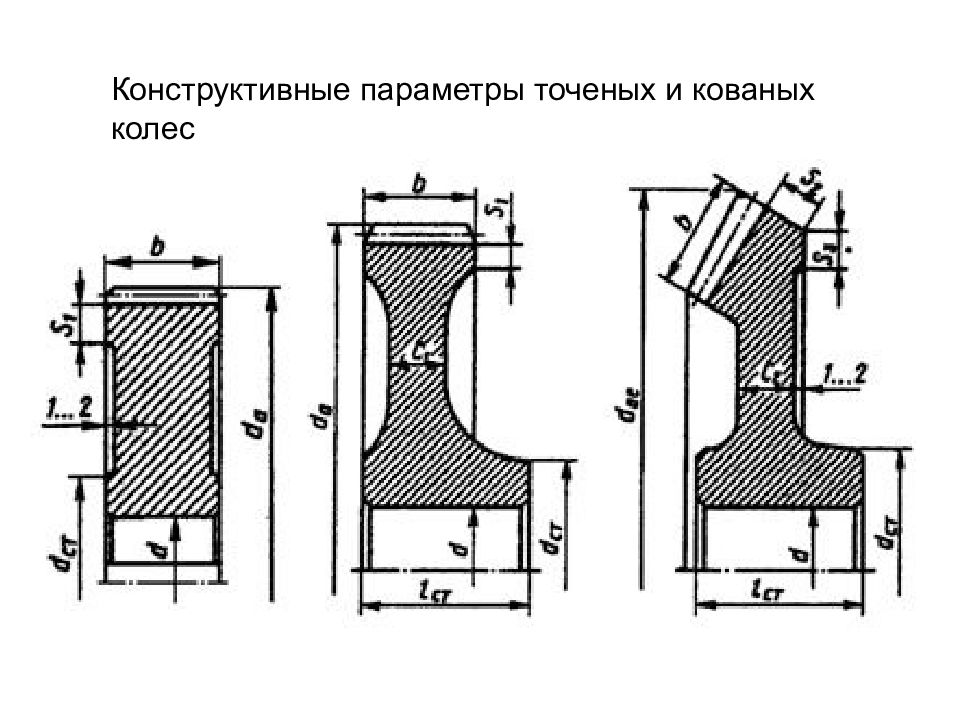
Толщина обода цилиндрических и конических зубчатых колес может быть выбрана по эмпирическому соотношению , в котором: m – модуль зацепления (для конических колес следует использовать внешний модуль me (mte)), b – ширина зубчатого венца.
Толщину диска принимают равной: для цилиндрических колёс для конических колёс
Диаметр ступицы - dст = 1,55×d Длина ступицы - lст = (0,8…1,5)×d где d – посадочный диаметр вала.
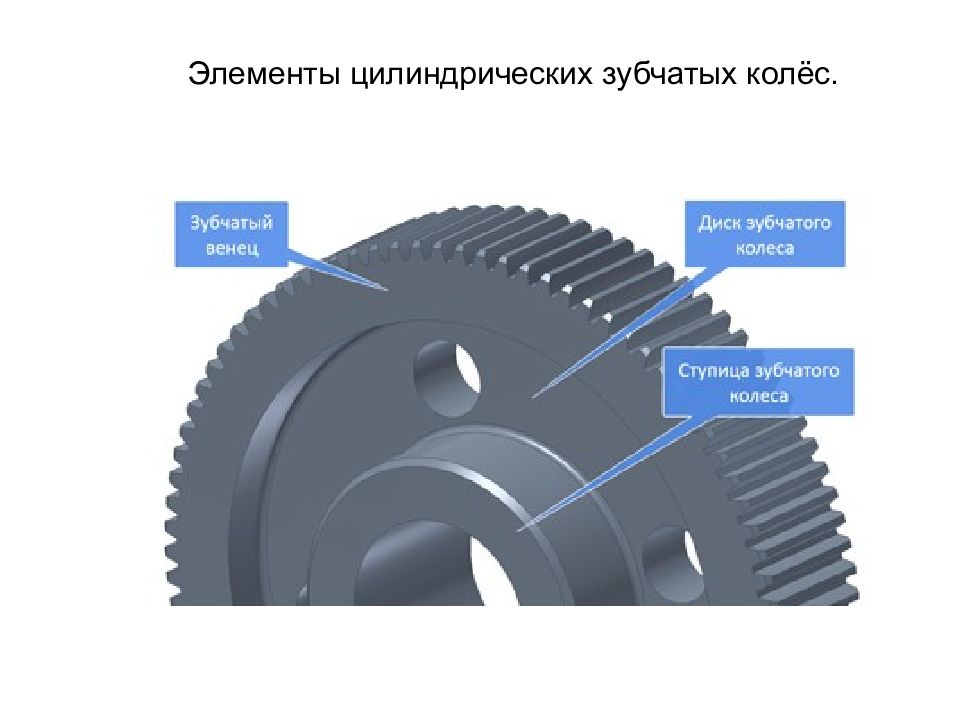
У колес большого диаметра с целью экономии легированной стали иногда применяют насадной зубчатый венец (сборные зубчатые колёса), который крепится на ободе так, чтобы исключить возможность его проворачивания.
