Первый слайд презентации
Лекция № 7 (Часть-2) Элементы квантовой статистики И физики твёрдого тела
Слайд 2: План лекции
Понятие о квантовых статистиках Бозе – Эйнштейна и Ферми – Дирака. Вырожденный электронный газ в металлах. Теплоемкость кристаллов (классическая теория). Теплоемкость кристаллов по Эйнштейну. Теплоемкость кристаллов по Дебаю.
Слайд 4: Квантовая статистика
Квантовой статистикой называется статистический метод исследования, применяемый к системам, которые состоят из большого числа частиц и подчиняются законам квантовой механики.
Слайд 5: Квантовая статистика строится
из принципа неразличимости тождественных частиц : все одинаковые частицы ( например, все электроны в металлах, все протоны в ядрах атомов ) считаются принципиально неразличимыми друг от друга. Квантовая статистика строится
Слайд 9
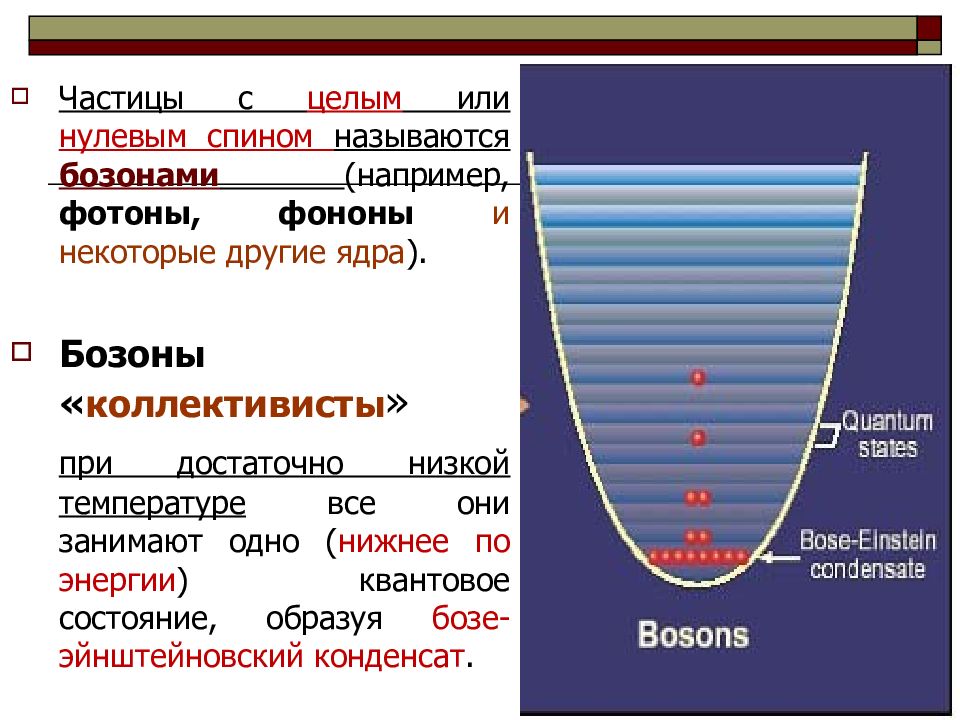
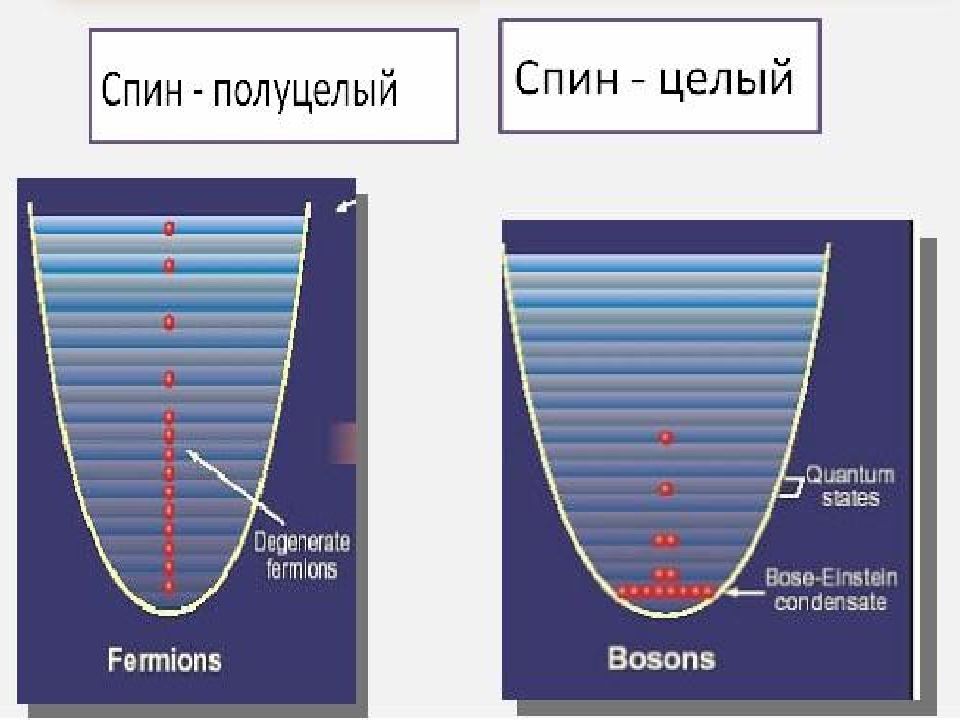
Частицы с целым или нулевым спином называются бозонами (например, фотоны, фононы и некоторые другие ядра ). Бозоны « коллективисты » при достаточно низкой температуре все они занимают одно ( нижнее по энергии ) квантовое состояние, образуя бозе-эйнштейновский конденсат.
Слайд 10
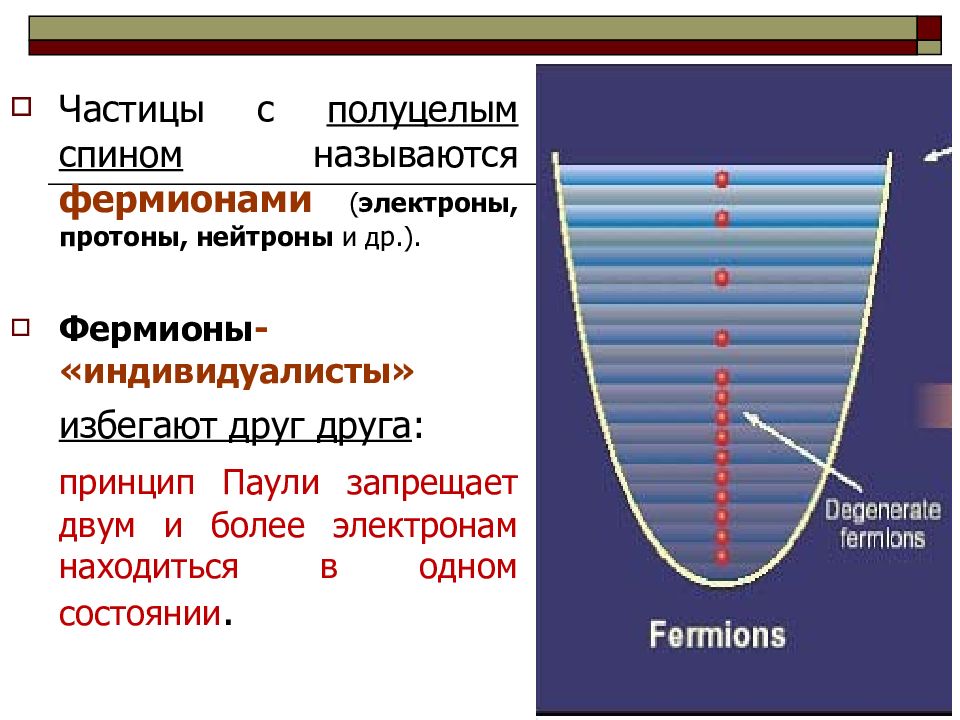
Частицы с полуцелым спином называются фермионами ( электроны, протоны, нейтроны и др.). Фермионы - «индивидуалисты» избегают друг друга : принцип Паули запрещает двум и более электронам находиться в одном состоянии.
Слайд 11: Объект изучения квантовой статистики
Одним из важнейших «объектов» изучения квантовой статистики как и классической, является идеальный газ.
Слайд 12: Основная задача квантовой статистики
задача о распределении частиц по координатам и скоростям.
Слайд 13: Понятие о квантовых статистиках Бозе – Эйнштейна
Системы бозонов описывается квантовой статистикой Бозе – Эйнштейна. Распределение Бозе — Эйнштейна — формула, описывающая распределение по уровням энергии тождественных частиц с нулевым или целочисленным спином при условии, что взаимодействие частиц в системе слабое и им можно пренебречь ( функция распределения идеального квантового газа, подчиняющегося статистике Бозе — Эйнштейна ).
Слайд 14
Распределение Бозе – Эйнштейна имеет вид где - среднее число бозонов в квантовом состоянии с энергией; k – постоянная Больцмана; Т – термодинамическая температура; РАСПРЕДЕЛЕНИЕ Б-Э
Слайд 17: Химический потенциал
Химический потенциал Он не зависит от энергии, а определяется только температурой и плотностью числа частиц. Кроме того, химический потенциал является работой, которая совершается в изобарно – изотермических условиях при увеличении числа частиц в системе на единицу.
Слайд 18
Распределение Бозе-Эйнштейна используется для описания свойств систем, состоящих из бозе-частиц. С его помощью описываются свойства теплового излучения, теплоемкость кристаллов и многие другие физические явления.
Слайд 19
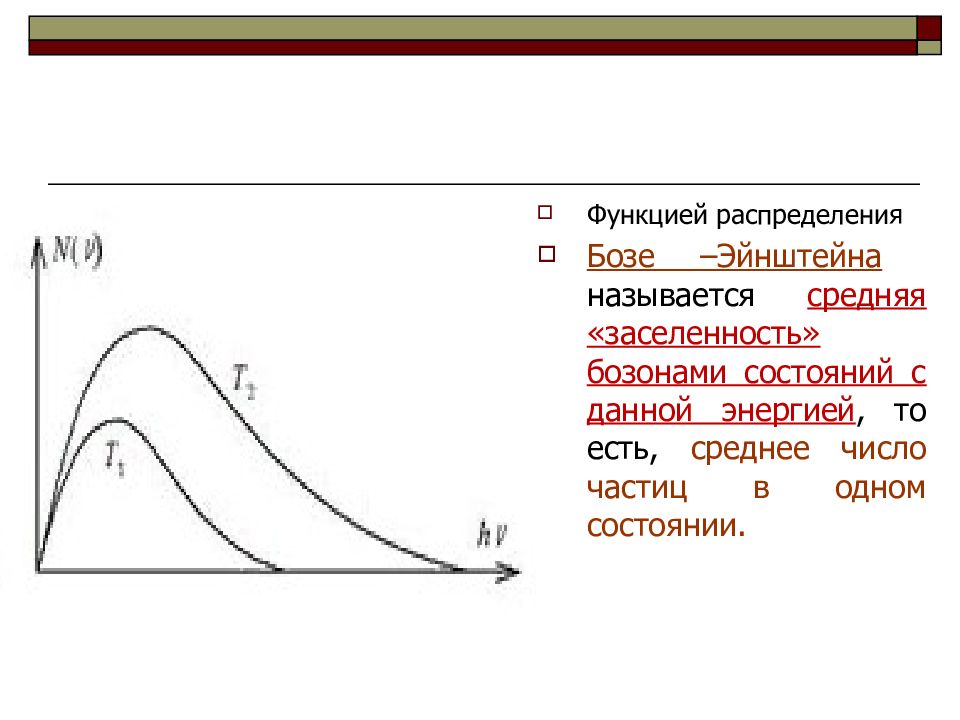
Функцией распределения Бозе –Эйнштейна называется средняя «заселенность» бозонами состояний с данной энергией, то есть, среднее число частиц в одном состоянии.
Слайд 20
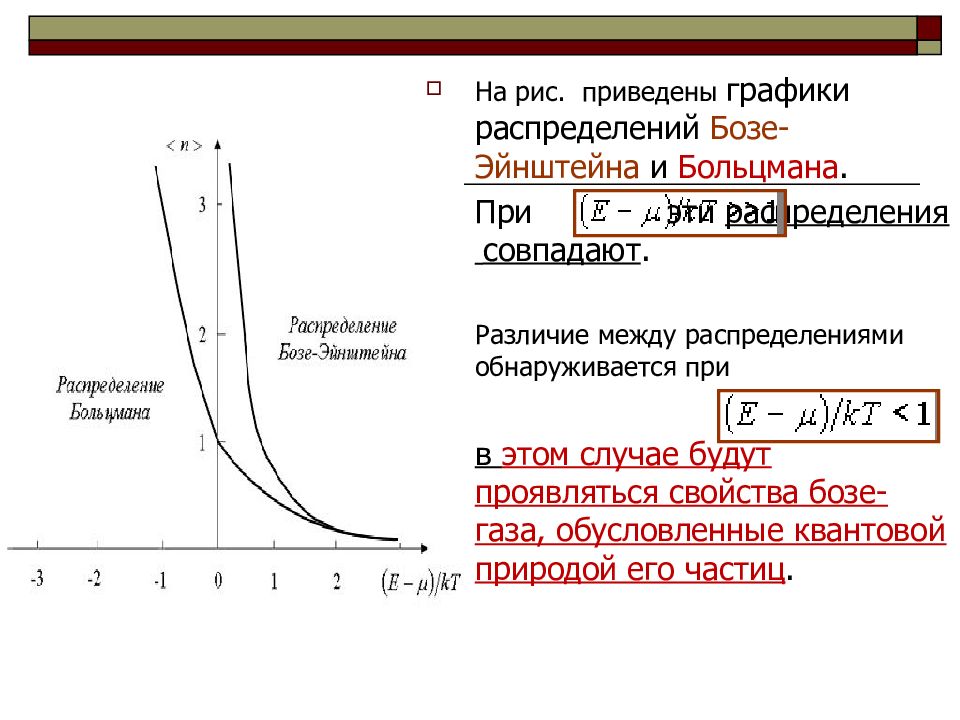
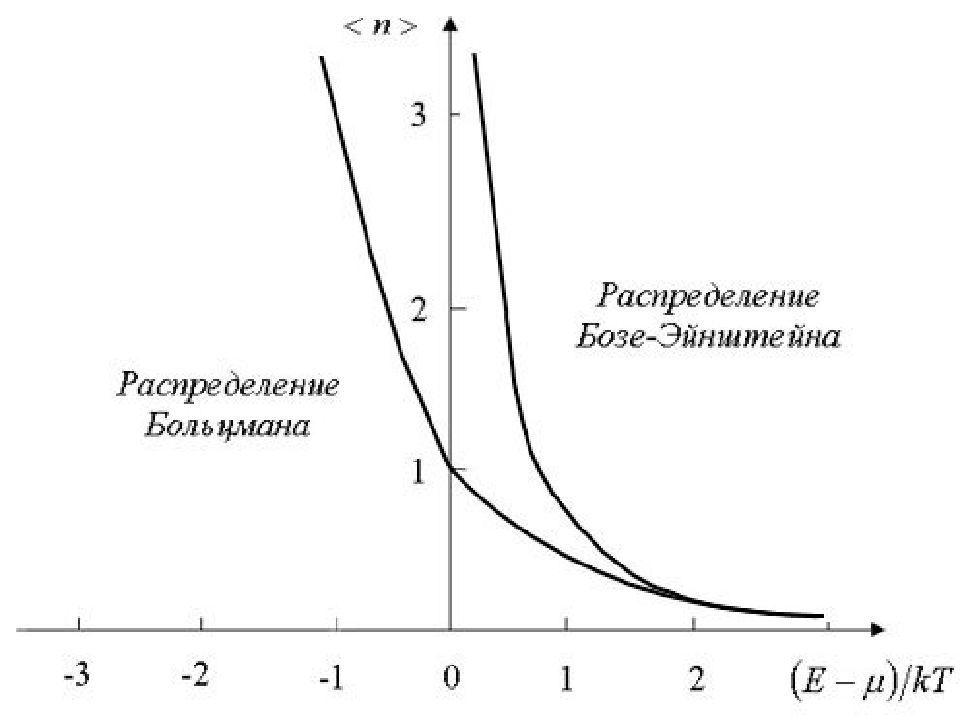
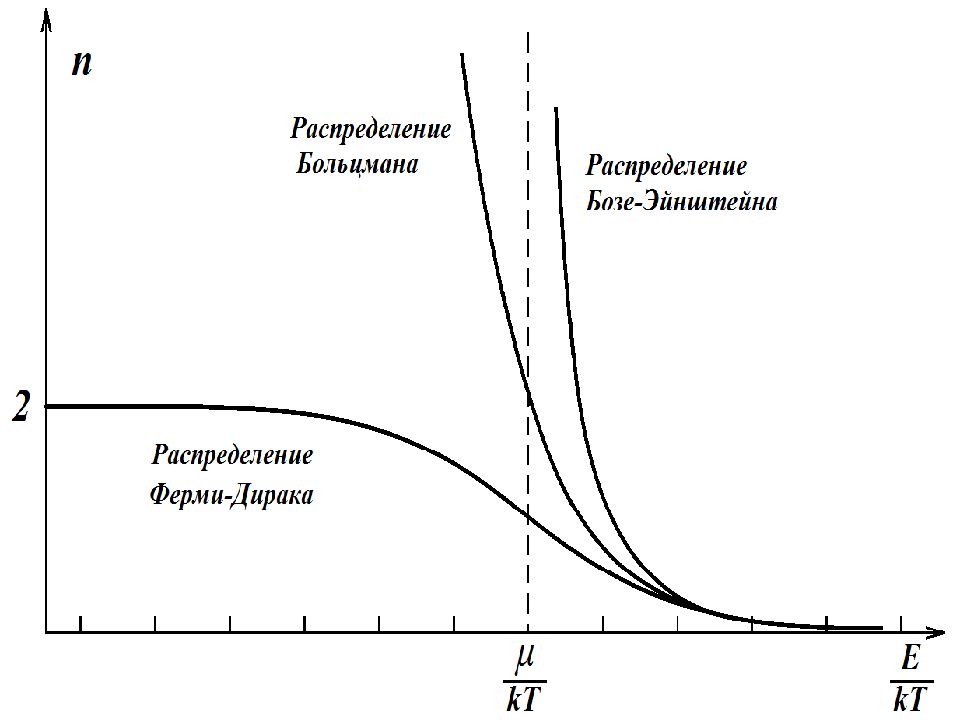
На рис. приведены графики распределений Бозе-Эйнштейна и Больцмана. При эти распределения совпадают. Различие между распределениями обнаруживается при в этом случае будут проявляться свойства бозе-газа, обусловленные квантовой природой его частиц.
Слайд 22: Понятие о квантовых статистиках Ферми – Дирака
Системы фермионов описываются антисимметричными волновыми функциями и подчиняются статистике Ферми-Дирака.
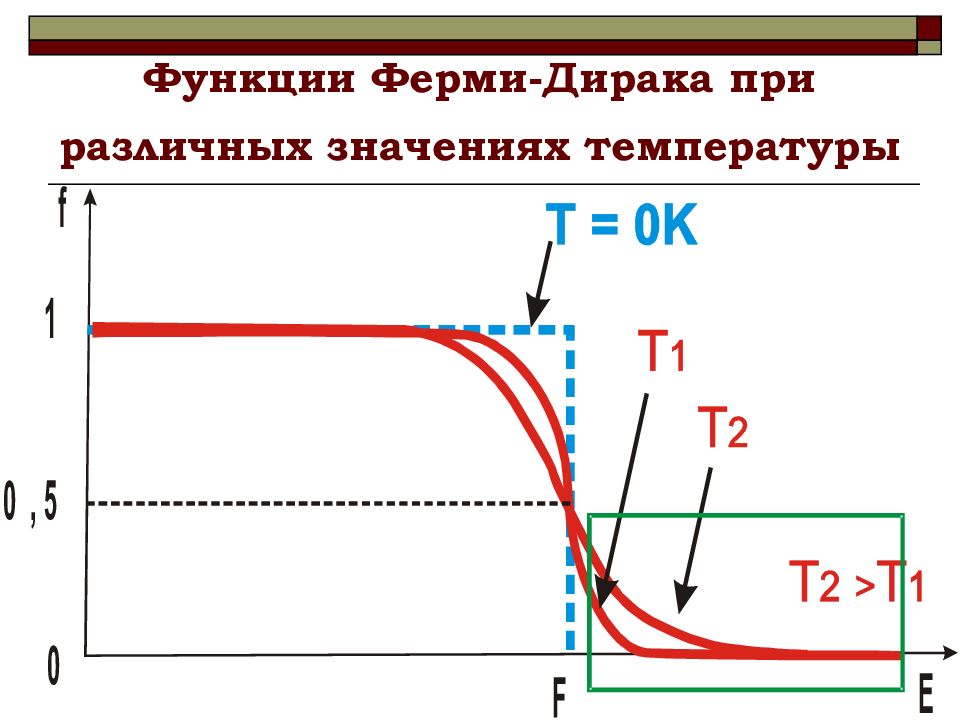
Слайд 24: Функции Ферми-Дирака
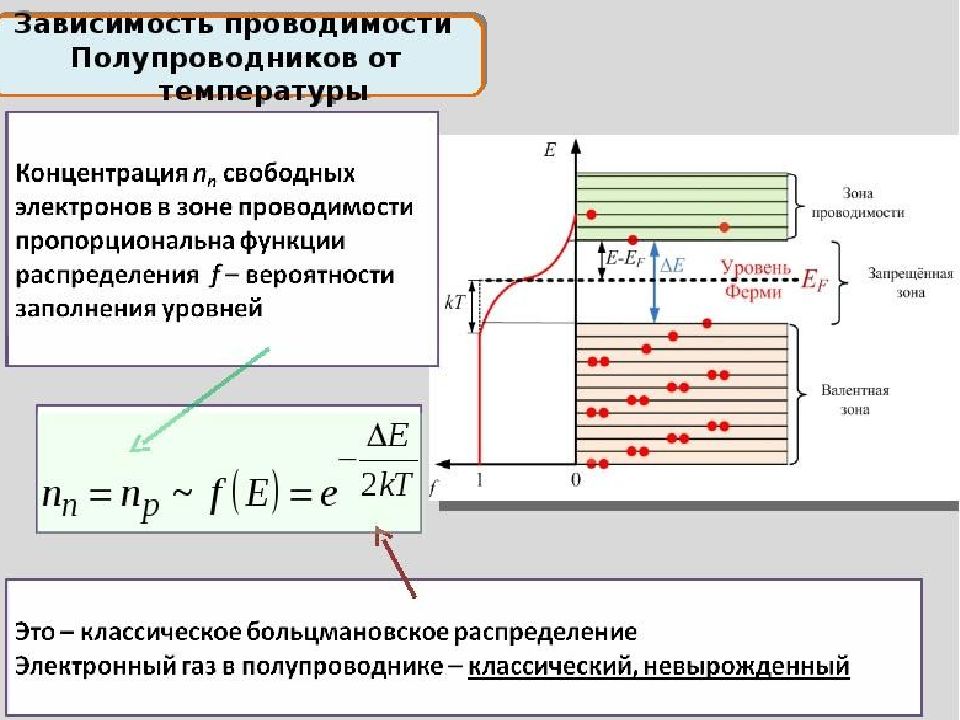
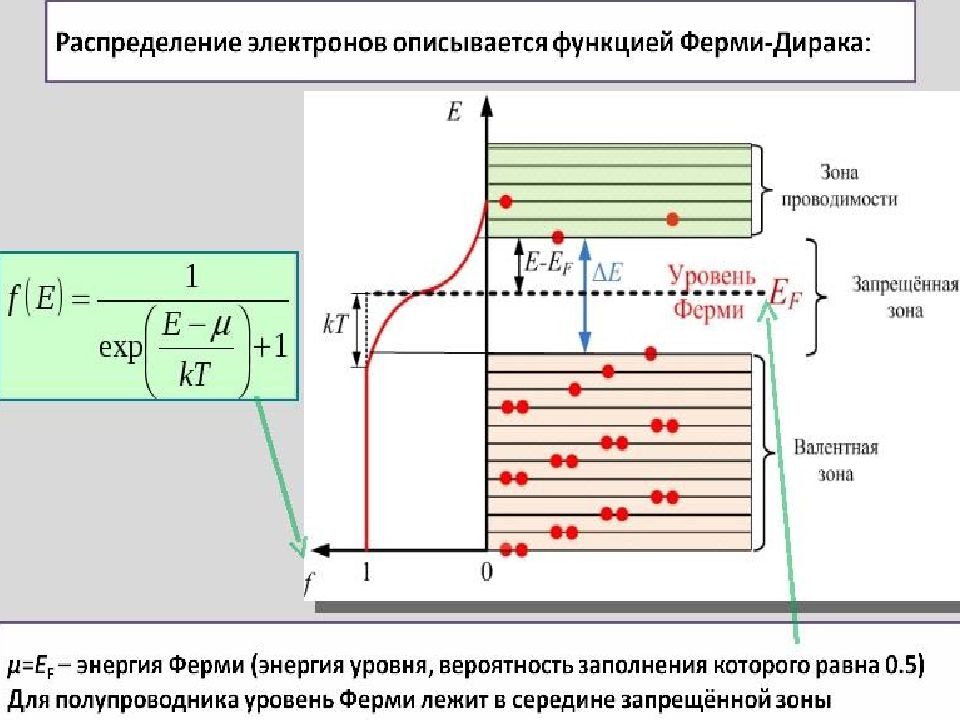
В термодинамическом равновесии электроны распределяются по энергетическим состояниям в соответствии с функцией распределения Ферми - Дирака :
Слайд 25
где f ( E, T ) – вероятность нахождения электрона в состоянии с энергией E ; T – температура системы (К); k – постоянная Больцмана; Е F – энергия уровня Ферми (это характеристическая энергия системы, ниже которой при T = 0 K все состояния заполнены, выше – пустые ).
Слайд 26
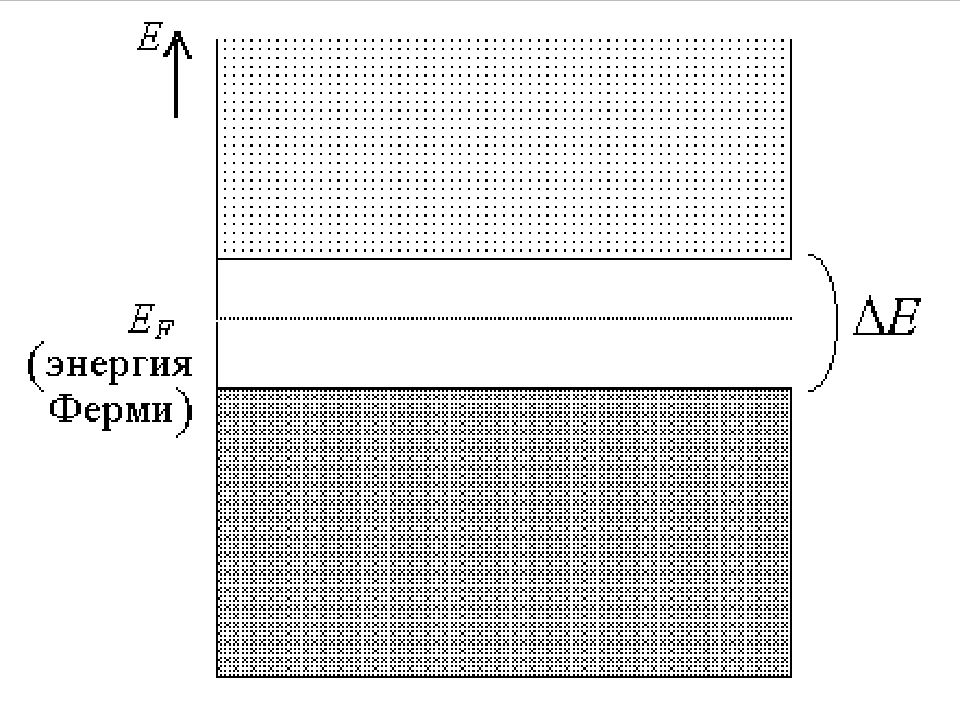
Уровень Ферми уровень, вероятность нахождения электрона на котором равна 0,5 должен находиться между зоной проводимости и валентной зоной, т.е. лежать в запрещенной зоне. Почему???
Слайд 35
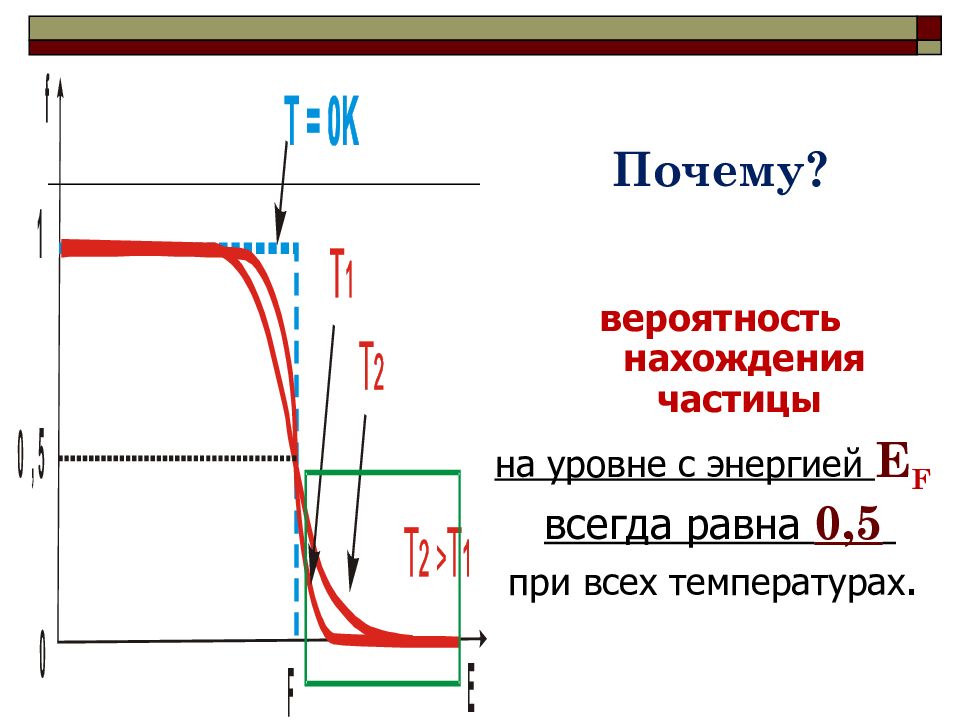
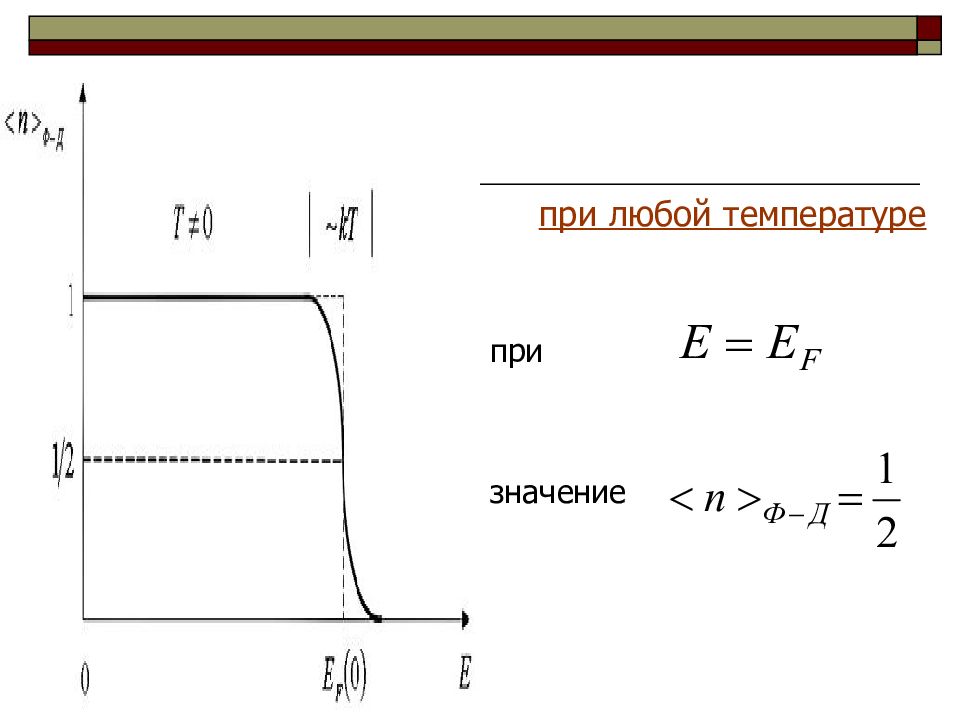
Почему? вероятность нахождения частицы на уровне с энергией Е F всегда равна 0,5 при всех температурах.
Слайд 36
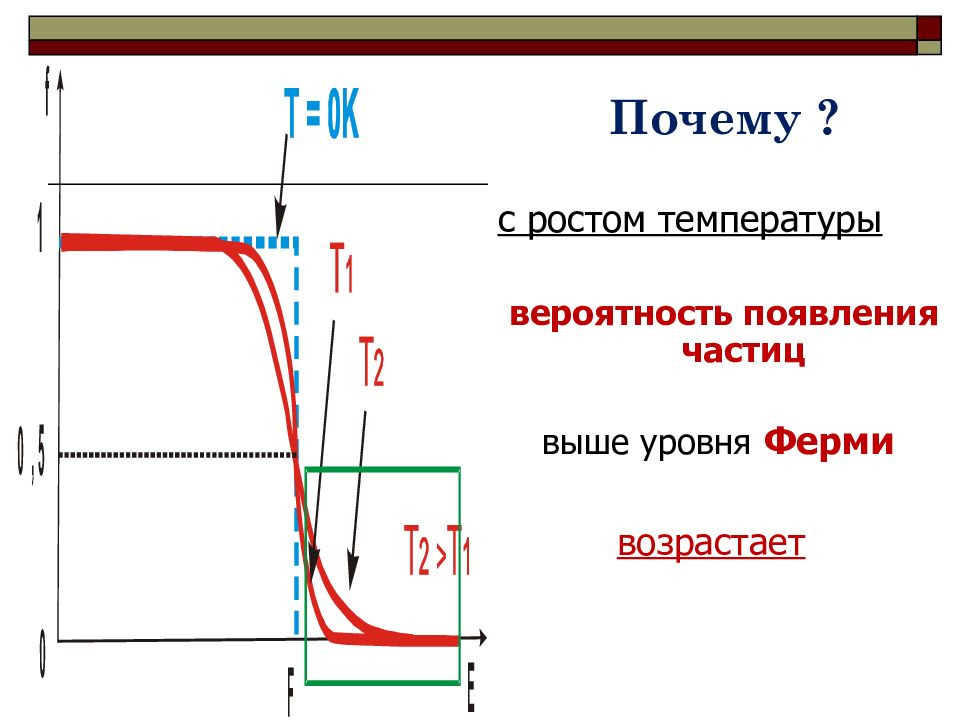
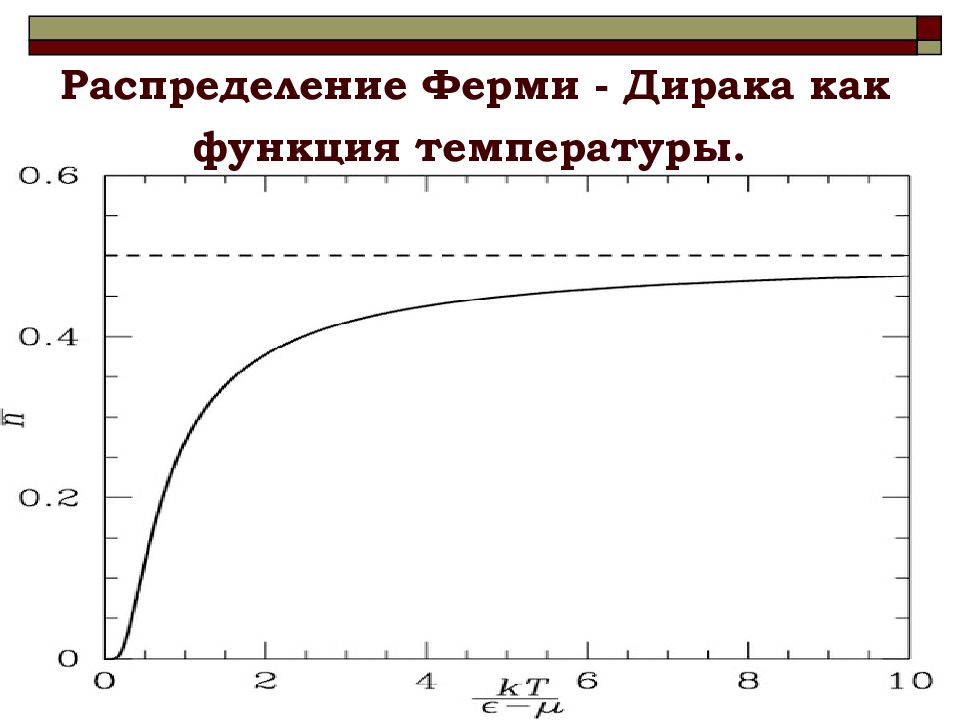
Почему ? с ростом температуры вероятность появления частиц выше уровня Ферми возрастает
Слайд 37
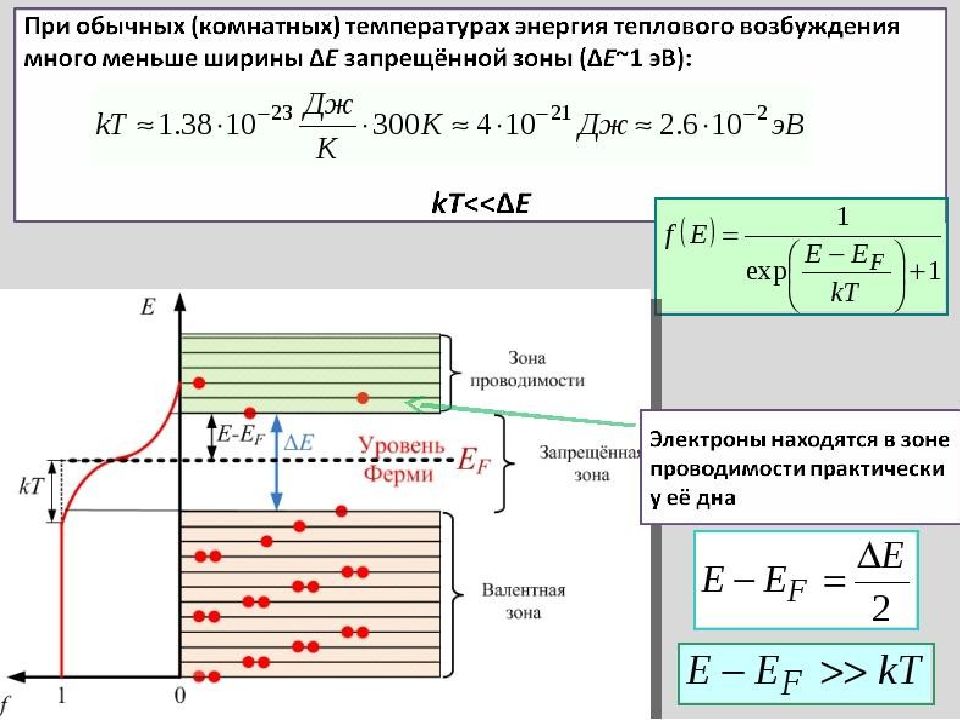
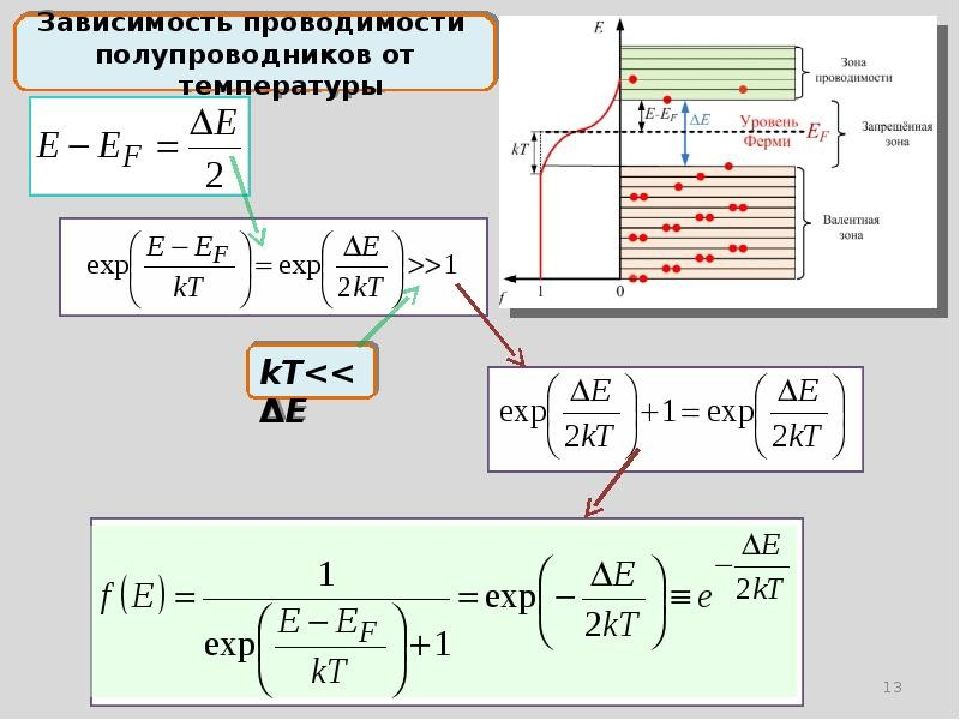
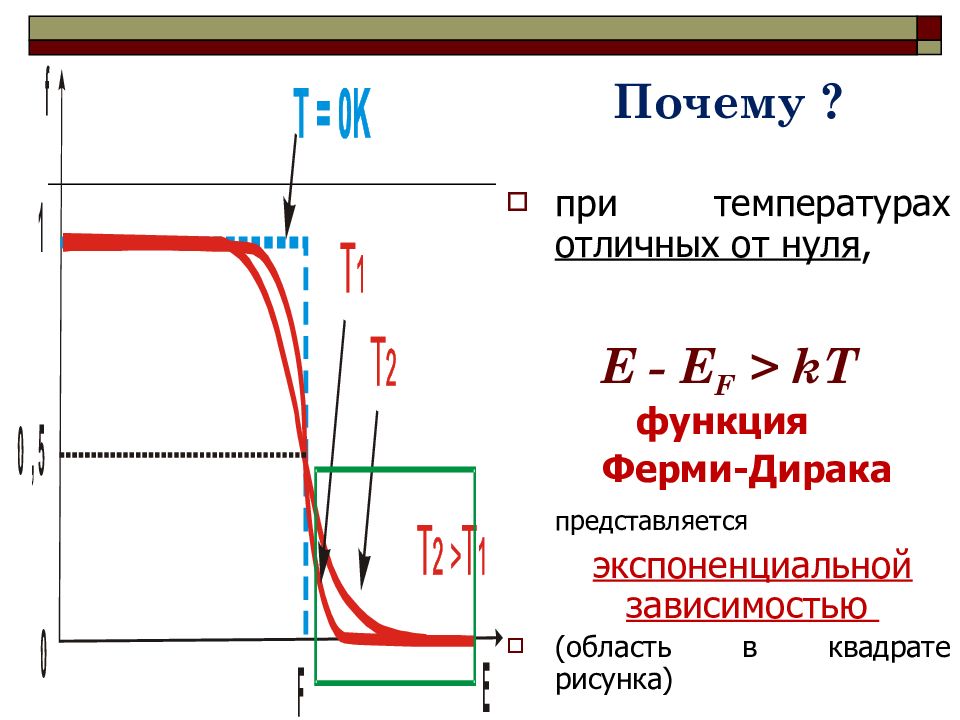
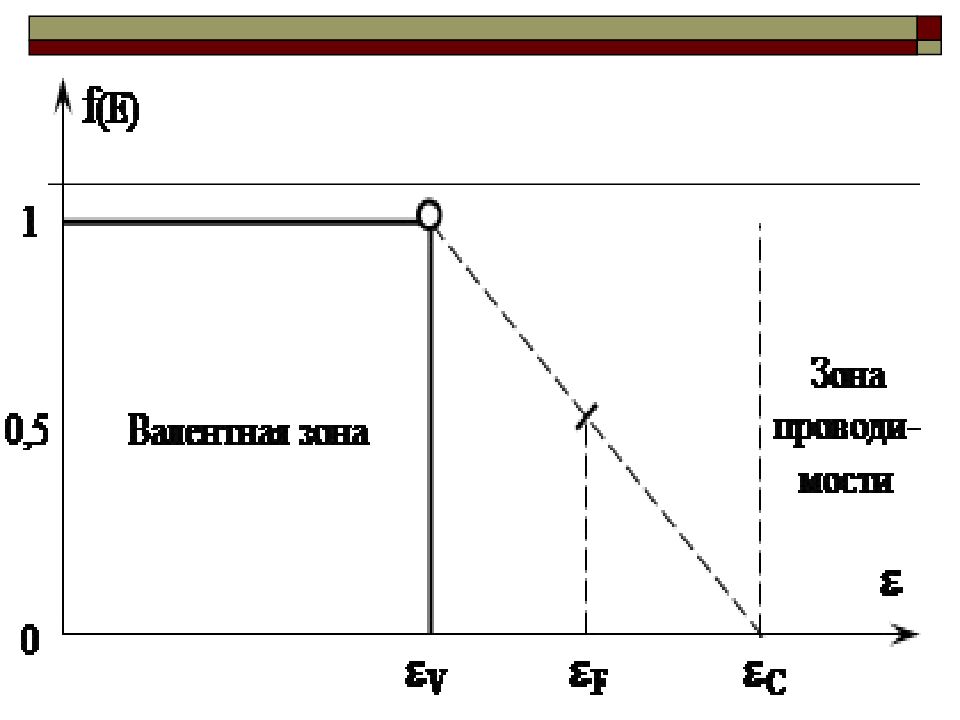
Почему ? при температурах отличных от нуля, E - Е F > kT функция Ферми-Дирака представляется экспоненциальной зависимостью (область в квадрате рисунка)
Слайд 38: Распределение Ферми – Дирака
Распределение Ферми – Дирака имеет вид где - среднее число фермионов в квантовом состоянии с энергией Е i.
Слайд 40: Распределение Ферми-Дирака
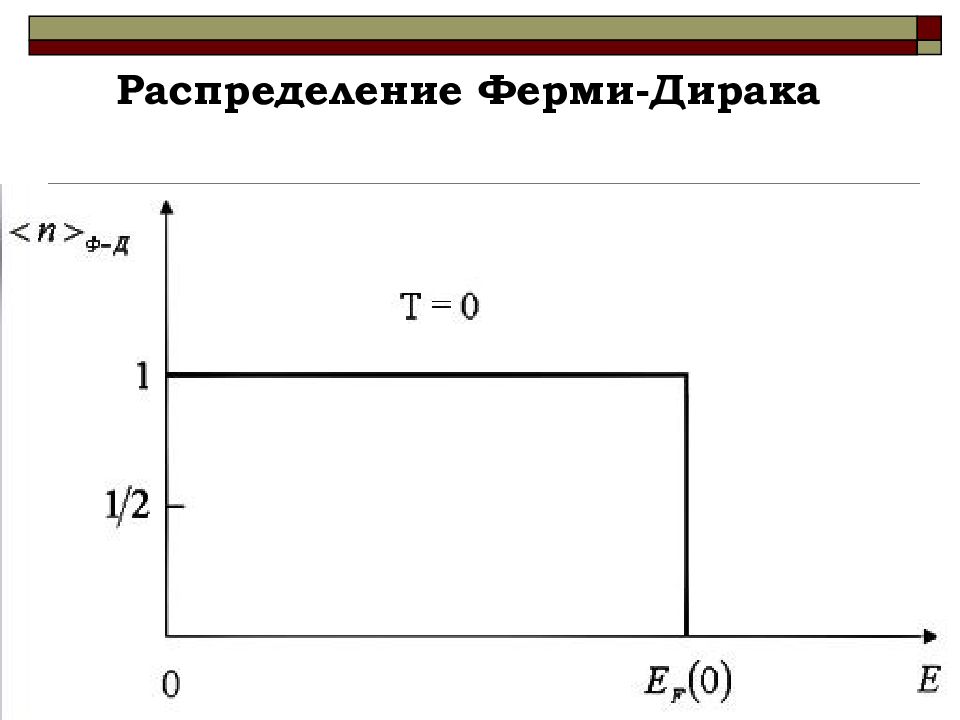
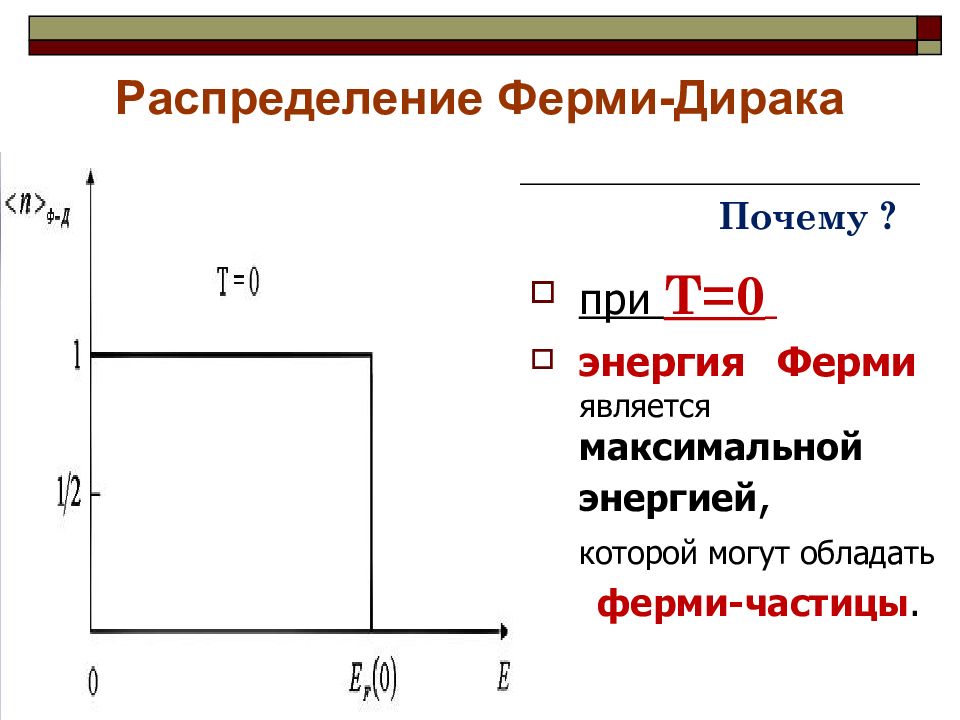
при Т=0 энергия Ферми является максимальной энергией, которой могут обладать ферми-частицы. Почему ?
Слайд 41: Распределение Ферми-Дирака
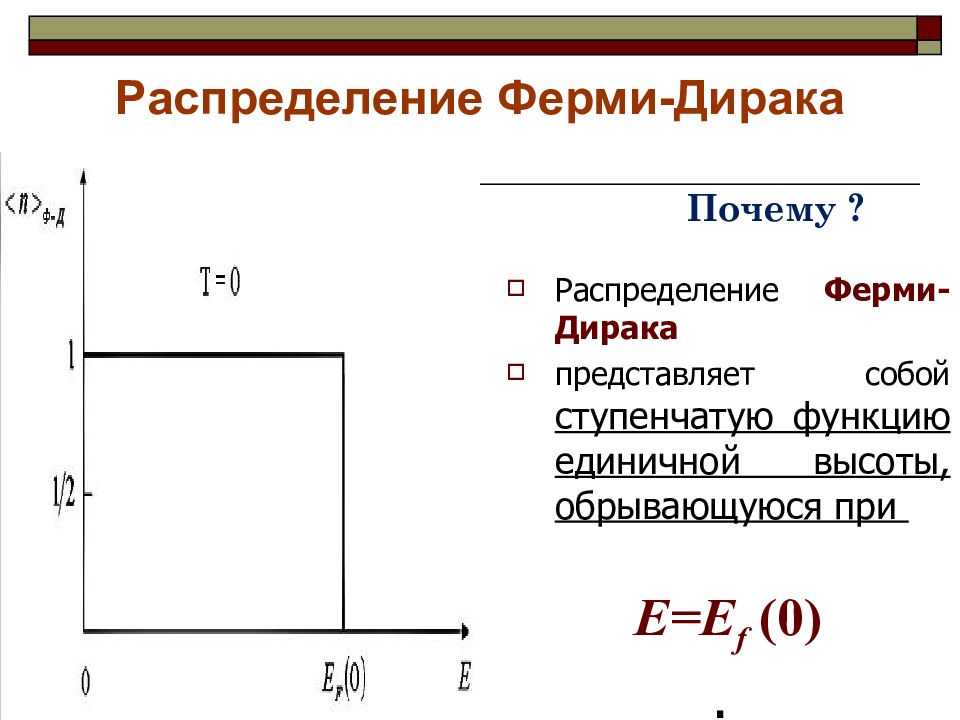
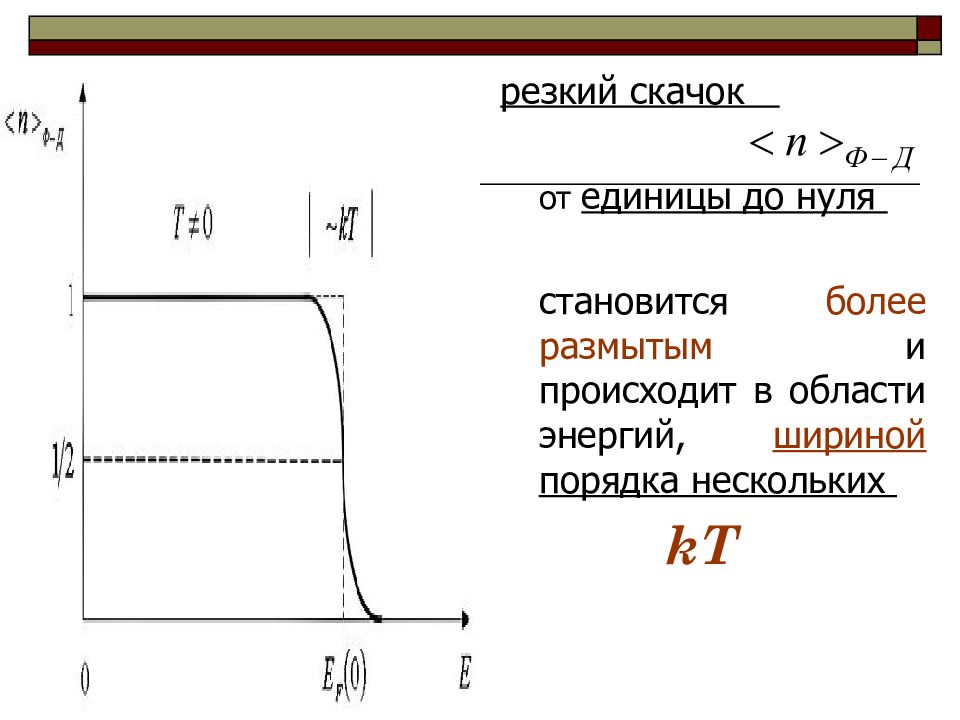
Распределение Ферми-Дирака представляет собой ступенчатую функцию единичной высоты, обрывающуюся при E=E f (0) . Почему ?
Слайд 43
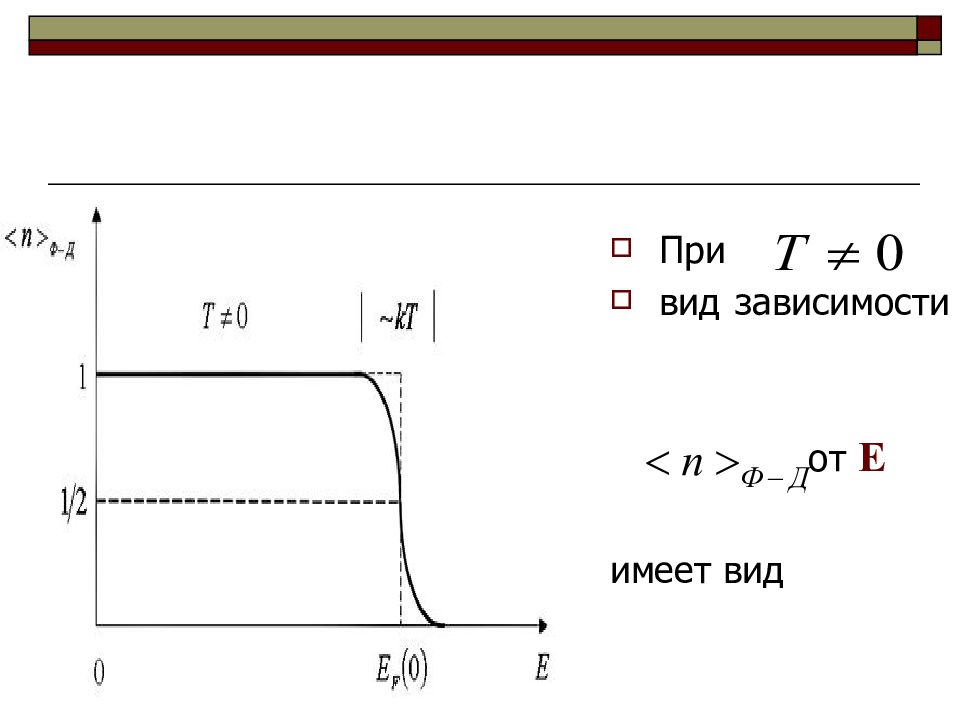
резкий скачок от единицы до нуля становится более размытым и происходит в области энергий, шириной порядка нескольких kT
Слайд 44
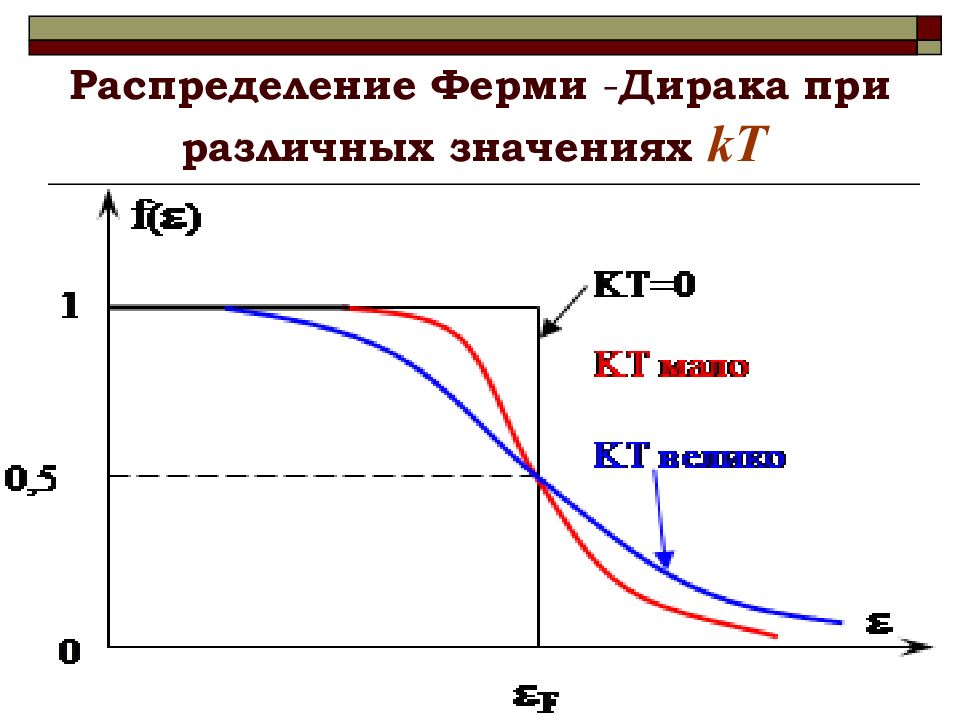
Чем выше температура, тем шире область, в которой меняется от единицы до нуля, и тем более плавно происходит переход от заполненных состояний к незаполненным.
Слайд 47
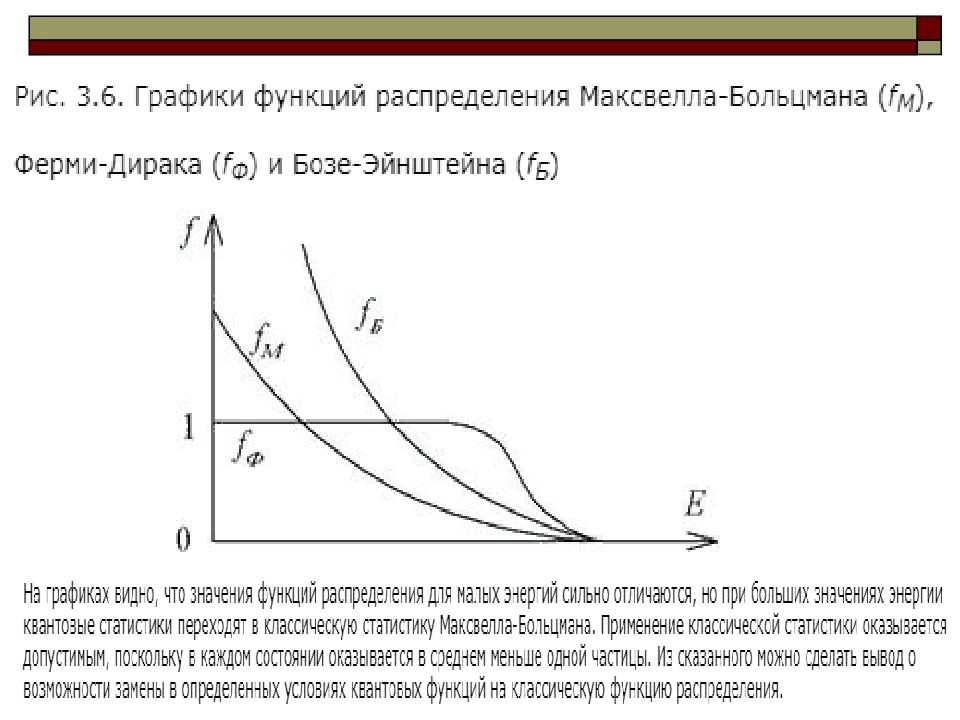
Если то распределения Бозе – Эйнштейна и Ферми – Дирака переходят в классическое распределение Максвелла – Больцмана где А – параметр вырождения, он определяется следующим образом
Слайд 53: Вырожденная система частиц
Система частиц называется вырожденной, если ее свойства, описываемые квантовыми закономерностями, отличаются от свойств обычных систем, подчиняющихся классическим законам.
Слайд 54: Вырожденный газ
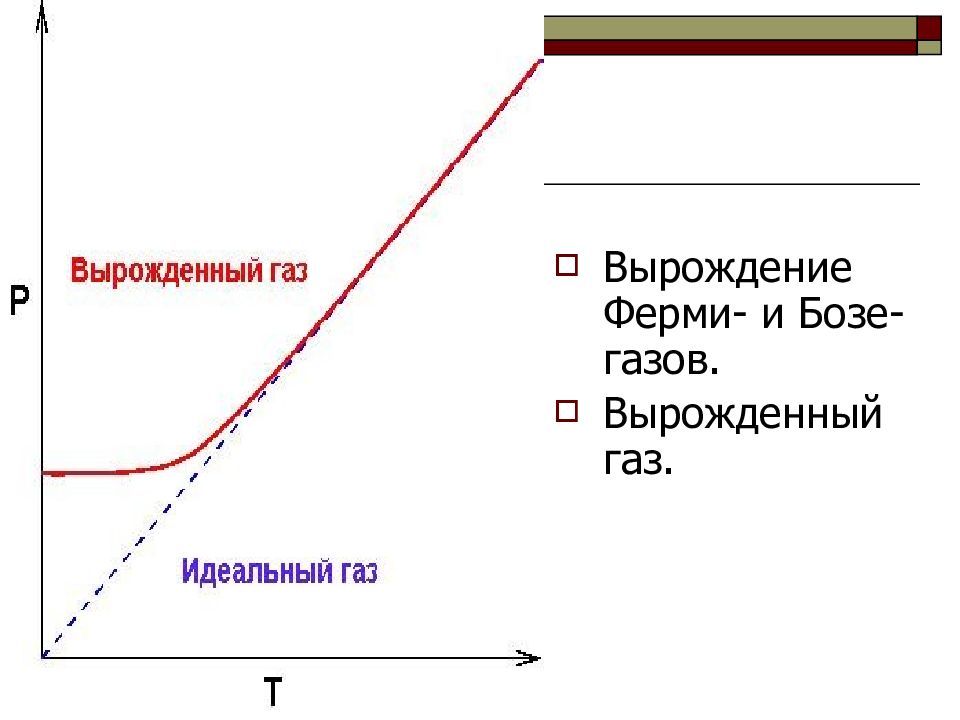
Отступление в поведении бозе – и ферми – газов от классического максвелл-больцмановского газа называется вырождением газов ( вырожденный газ ). Вырождение газов становится существенным при низких температурах и больших плотностях.
Слайд 57: Температура вырождения
Температурой вырождения Т В называется температура, при которой вырождение становится существенным. Она определяется из условия
Слайд 58: Температурный критерий вырождения
Т<< T B – система частиц вырождена, Т>>Т В – система частиц не вырождена, и ее поведение описывается классическими законами.
Слайд 59: Вырожденный электронный газ в металлах
Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми – Дирака где - среднее число электронов в квантовом состоянии с энергией Е ; - химический потенциал электронного газа при Т=0 К.
Слайд 62
Химический потенциал, является максимальной кинетической энергией, которой обладают электроны проводимости в металле при 0 К. Эта максимальная кинетическая энергия называется энергией Ферми и обозначается Е f Е f = Распределение Ферми – Дирака
Слайд 64: Уровень Ферми
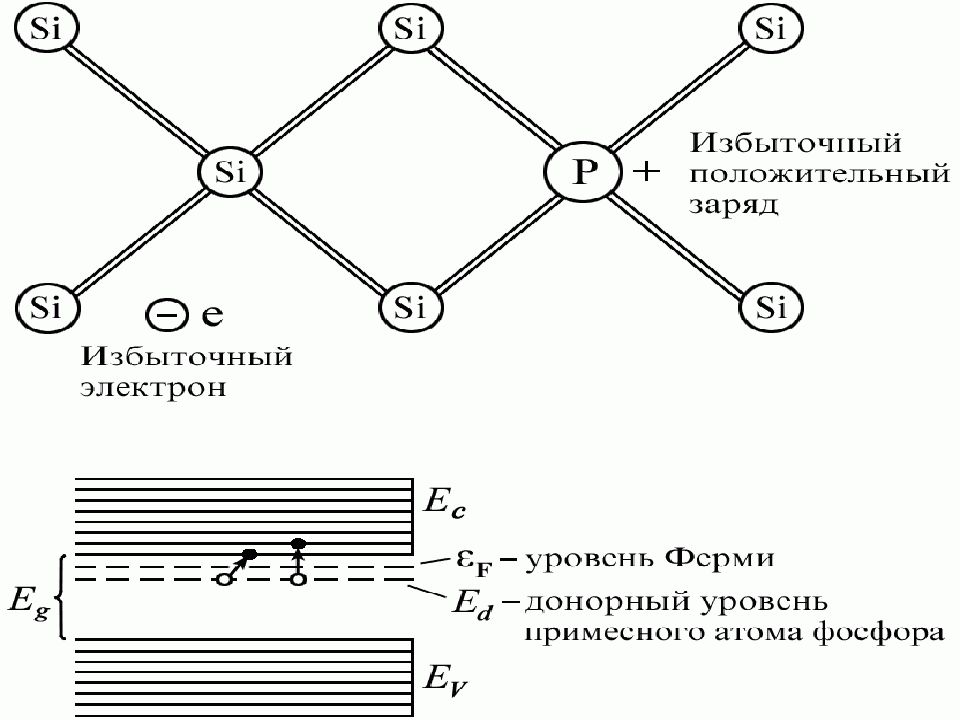
Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми. Уровню Ферми соответствует энергия Ферми, которую имеют электроны на этом уровне. Уровень Ферми будет тем выше, чем больше плотность электронного газа.
Слайд 67: Молярная теплоемкость электронного газа
Молярная теплоемкость электронного газа определяется следующим образом где N A – число Авогадро ; k – постоянная Больцмана.
Слайд 68
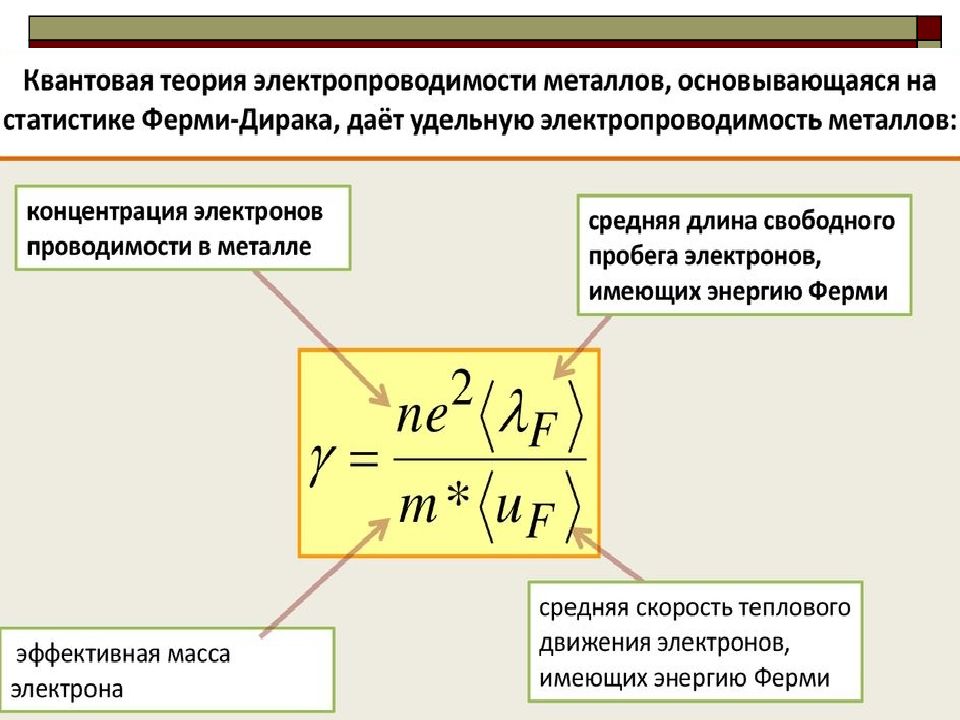
Теория электропроводности металлов, построенная на основе квантовой механики и квантовой статистики Ферми–Дирака, называется квантовой теорией электропроводности металлов.
Слайд 69: Теплоемкость кристаллов ( классическая теория )
В XIX в. Дюлонг и Пти при измерении теплоемкости твердых тел эмпирически установили закон : теплоемкость одноатомных кристаллов при комнатной температуре очень близка к значению С V = 25 Дж/(моль ·К) и мало изменяется с повышением температуры, стремясь к указанному значению.
Слайд 70: Классическая модель внутреннего строения твердых тел
одноатомный кристалл - совокупность атомов, колеблющихся в узлах кристаллической решетки под действием упругих сил.
Слайд 71
Колебания каждого атома можно описать тремя степенями свободы. Таким образом, твердое тело в этом случае можно представить как совокупность классических осцилляторов, число которых в одном моле равно числу Авогадро. Внутренняя энергия моля кристалла будет равна а молярная теплоемкость
Слайд 73
не объясняет : температурной зависимости теплоемкости, разницы в поведении диэлектриков и металлов при очень низких температурах
Слайд 74
не объясняет : исключений из закона Дюлонга и Пти: алмаз, бериллий, бор, кремний и алюминий имеют при комнатной температуре теплоемкость, значительно меньшую 3 R. При повышении температуры этих веществ их теплоемкость растет, приближаясь к 3 R при существенно более высокой температуре. Строгую теорию теплоемкости можно построить лишь на базе квантовой механики.
Слайд 75: Теплоемкость кристаллов по Эйнштейну
Модель для объяснения температурного хода теплоемкости кристаллов
Слайд 76
Каждый атом представляет собой осциллятор, колеблющийся с некоторой частотой, одинаковой для всех атомов кристалла. В отличие от классической модели здесь рассматривается квантовый осциллятор, энергия которого может принимать только дискретные значения, кратные, где - частота колебаний осциллятора.
Слайд 77: Теплоемкость твердых тел
Теплоемкость твердых тел по Эйнштейну будет определена следующим образом
Слайд 79: Температура Эйнштейна
введём характерный параметр где - температура Эйнштейна
Слайд 82
Модель дает качественно верную температурную зависимость теплоемкости диэлектриков, не давая при этом хорошего количественного совпадения с экспериментом, особенно при низких температурах. Следующим шагом в развитии представлений о взаимодействии атомов в кристаллической решетке явилась модель Дебая
Слайд 83: Теплоемкость кристаллов по Дебаю
Дебай предложил рассматривать совокупность атомов кристалла как упругую среду, ограниченную размером кристалла, в которой коллективные колебания атомов представляются суперпозицией собственных типов колебаний такой среды.
Слайд 84: Внутренняя энергия кристалла
Определим внутреннюю энергию кристалла где - температура Дебая. Теплоемкость при низких температурах в одноатомном кристалле изменяется пропорционально Т 3.
Слайд 87: Фонон. Энергия фонона
Фонон - квант энергии звуковой волны (так как упругие волны – волны звуковые ). Фононы являются квазичастицам и – элементарными возбуждениями, ведущими себя подобно микрочастицам. Энергия фонона
Слайд 88: Импульс фонона
Импульс фонона обладает своеобразным свойством: при столкновении фононов в кристалле их импульс может дискретными порциями передаваться кристаллической решетке – он при этом не сохраняется. Поэтому в случае фононов говорят о квазиимпульсе.
Слайд 89
Энергия кристаллической решетки рассматривается как энергия фононого газа, подчиняющегося статистике Бозе – Эйнштейна, так как фононы являются бозонами ( их спин равен нулю ).
Слайд 90: Распределение Бозе-Эйнштейна
Распределение Бозе-Эйнштейна где < n i > - среднее число фононов частоты ω i.
Слайд 91: Бозон Хиггса – «божественная частица»,
Как и прежде, главной целью Большого коллайдера физики считают обнаружение таинственного бозона Хиггса – «божественной частицы», которая отвечает за массу элементарных частиц. Она состоит из двух кварков : так называемого прелестного кварка и его антагониста - прелестного антикварка.
Слайд 92
Новая частица поможет специалистам лучше понять, при помощи какой силы атомы соединяются друг с другом. Задание. Подготовить реферат на тему Бозон Хиггса – «божественная частица »,
Слайд 93
Отметим, что эксперименты по поиску бозона Хиггса пугают некоторых ученых своей непредсказуемостью - по одной из теорий, обнаружение этой частицы может привести к цепной реакции непроизвольного роста массы с образованием черной дыры, что грозит уничтожением всему живому.
Последний слайд презентации: Лекция № 7 (Часть-2) Элементы квантовой статистики И физики твёрдого тела: Физики надеются
Предполагается, что открытие "божественной частицы" позволит совершить революцию в науке, поможет значительно продвинуться в понимании фундаментальных законов физики и принципов строения Вселенной.