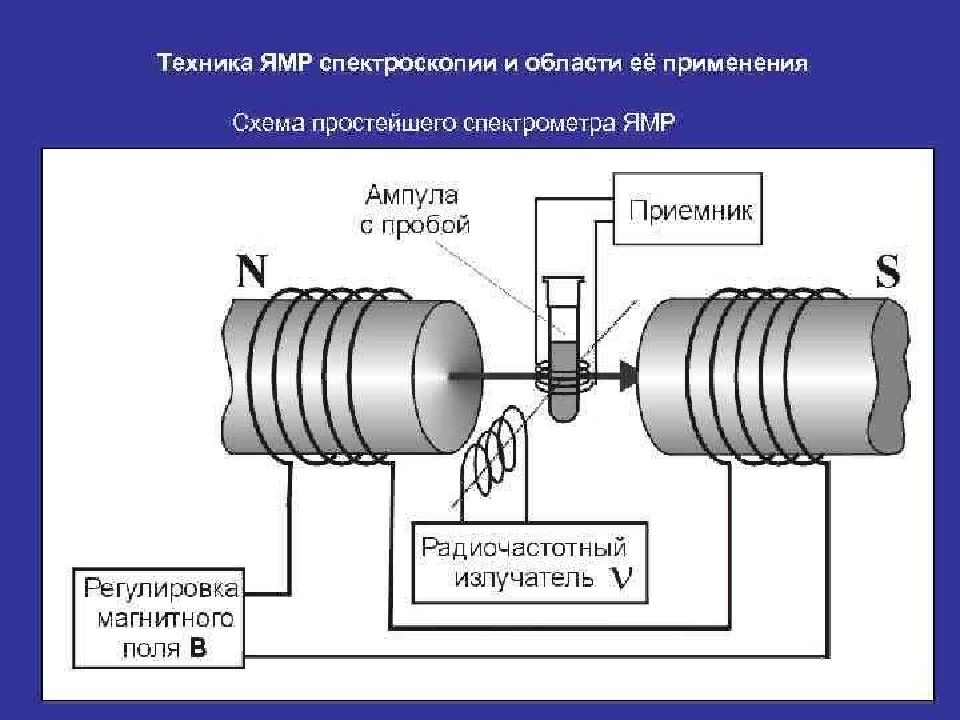
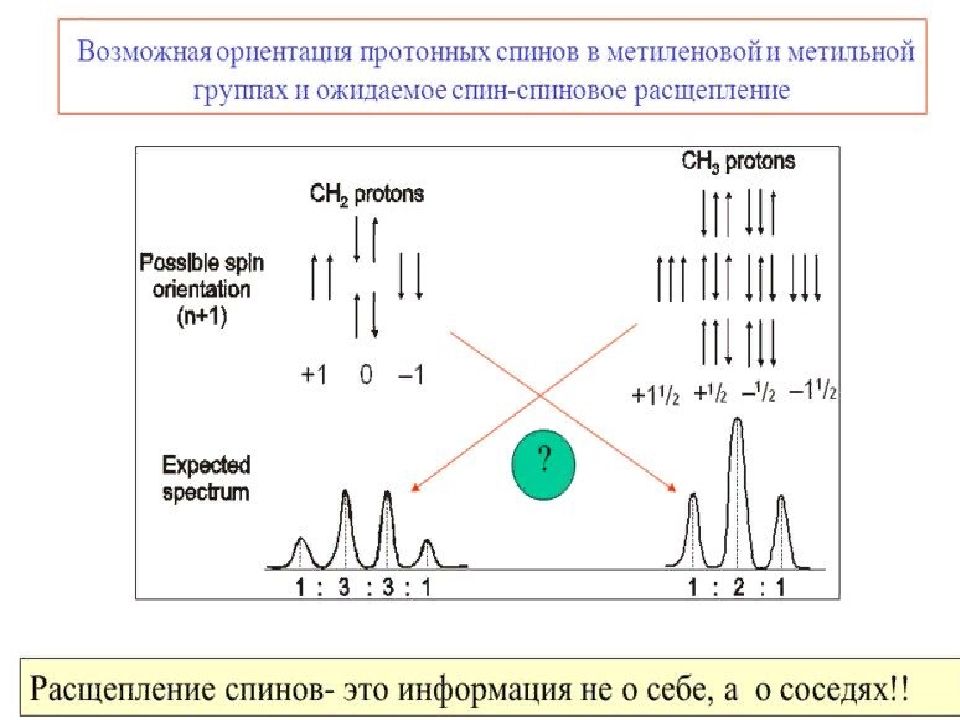
Первый слайд презентации: Лекция 4. Ядерно-магнитный резонанс
Явление ядерного магнитного резонанса (ЯМР) впервые обнаружено в 1945 году двумя группами американских физиков под руководством Ф. Блоха ( Стандфордский университет) и Э. Парселла (Гарвардский университет). В 1952 году за это открытие они были удостоены Нобелевской премии по физике.
Слайд 11
Вращающийся заряд создает магнитный момент который, так же как и угловой момент количества движения, квантован: Коэффициент пропорциональности γ в выражениях (2) и (3), называемый гиромагнитным отношением, наряду с ядерным спином I и природным содержанием (в %) является важнейшей характеристикой ядра.
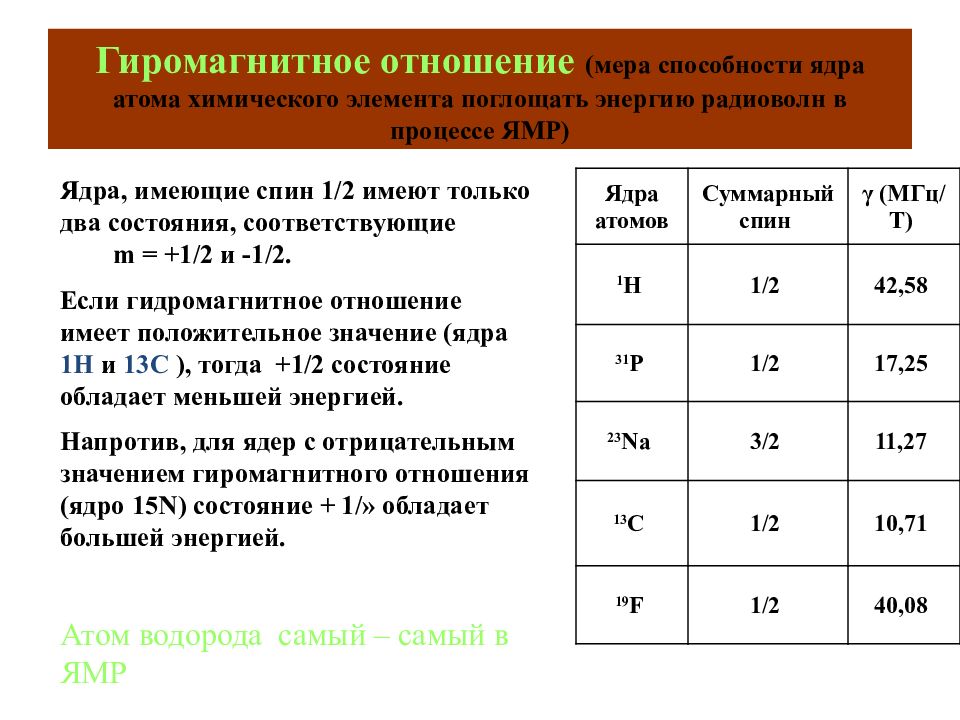
Ядра атомов Суммарный спин γ (MГц/T) 1 H 1/2 42,58 31 P 1/2 17,25 23 Na 3/2 11,27 13 C 1/2 10,71 19 F 1/2 40,08 Ядра, имеющие спин 1/2 имеют только два состояния, соответствующие m = +1/2 и -1/2. Если гидромагнитное отношение имеет положительное значение (ядра 1H и 13C ), тогда +1/2 состояние обладает меньшей энергией. Напротив, для ядер с отрицательным значением гиромагнитного отношения (ядро 15N) состояние + 1/» обладает большей энергией. Атом водорода самый – самый в ЯМР
Слайд 14: Ядра в статическом магнитном поле
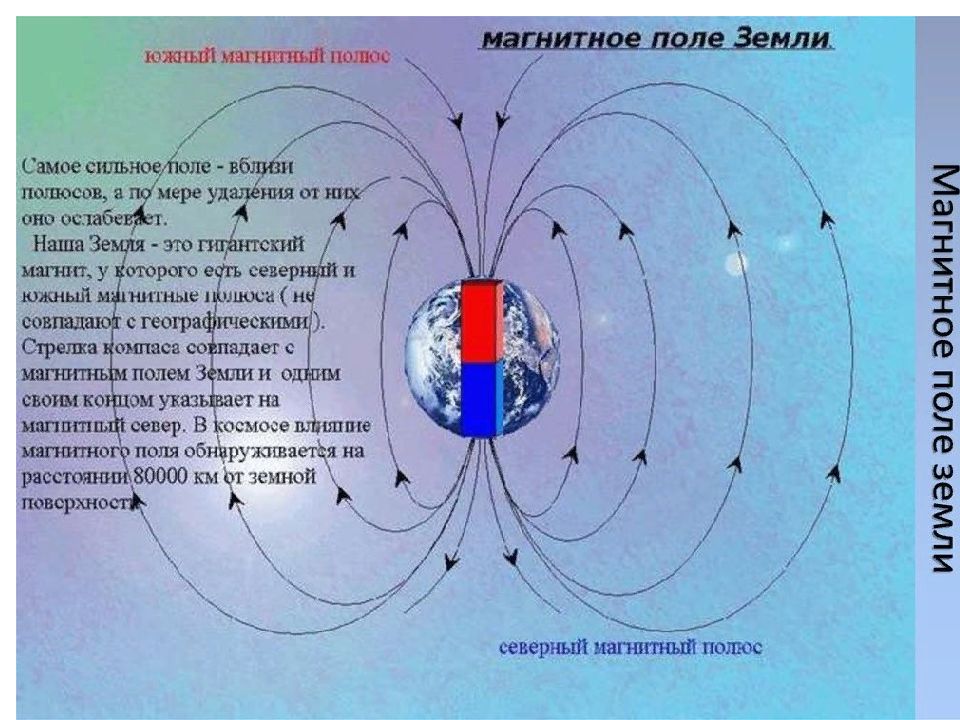
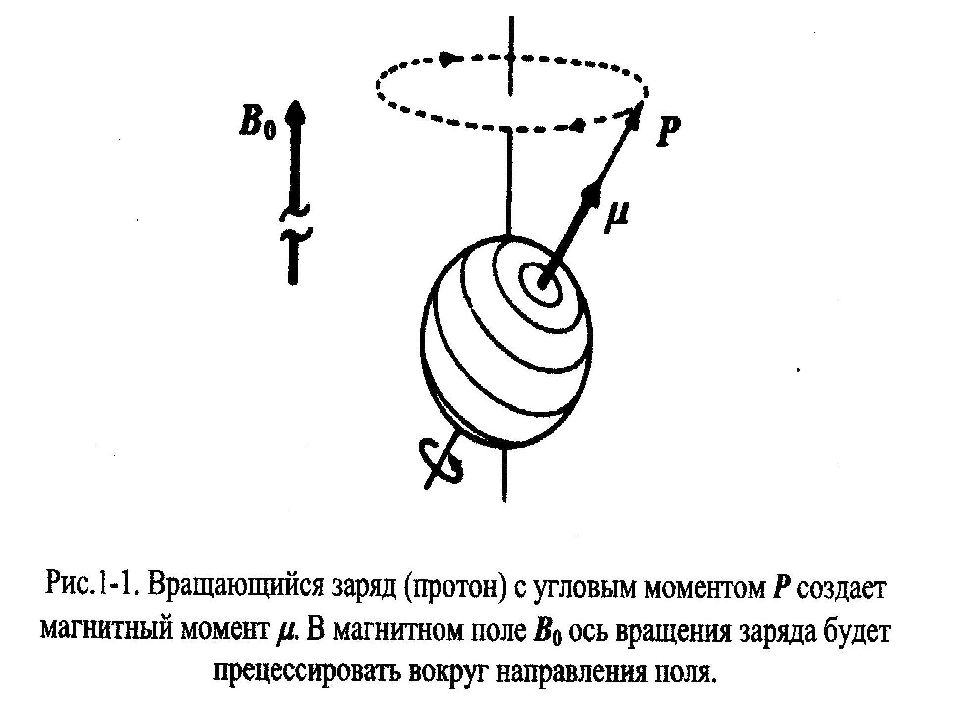
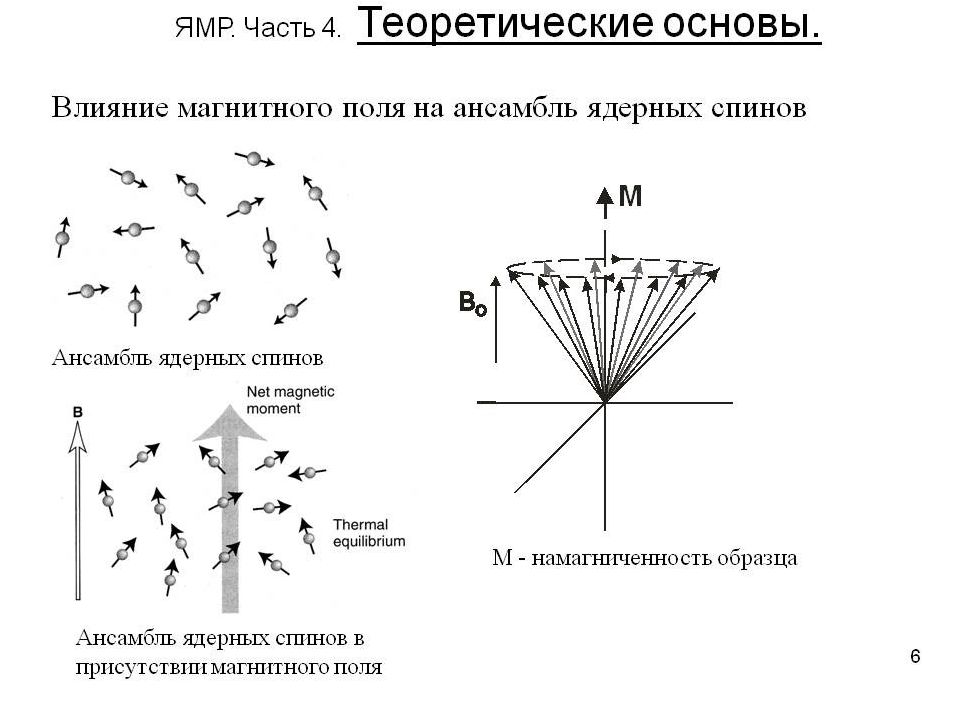
Если ядро с угловым моментом количества движения P и магнитным моментом поместить в статическое магнитное поле B, то возникнет его прецессия вокруг направления поля (рис. 1-1). Теперь, если расположить систему координат так, чтобы направление поля B совпадало с осью Z (рис. 1-2), то Z - компонента углового момента количества движения будет совпадать с направлением магнитного поля и определяться следующим соотношением:
Слайд 15
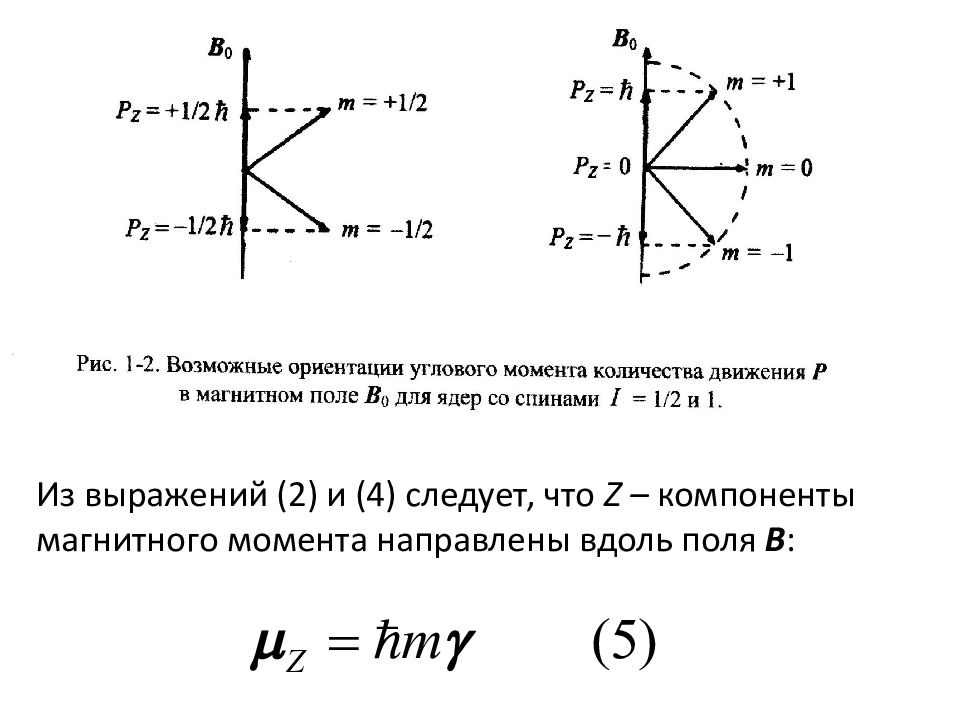
где m – магнитное квантовое число, которое принимает значения I, I-1, …, -I+1, -I. Очевидно, что m может принимать ( 2I+ 1) различных значений. Угловой и магнитный моменты имеют аналогичное число возможных ориентаций (квантование по направлению). Для ядер со спином I = 1/2 (например, 1 Н и 13 С) PZ = +1/2 и – 1/2 (две ориентации), а для ядер с I =1 ( 2 Н и 14 N) m = +1, 0 и –1 (три ориентации).
Слайд 16
Из выражений (2) и (4) следует, что Z – компоненты магнитного момента направлены вдоль поля B :
Слайд 17
С точки зрения квантово-механических представлений (в противоположность классическому описанию) разрешенными значениями угла прецессии считаются те, при которых проекция углового момента (спина) на ось Z имеет только целые или полуцелые значения I. Для ядер со спином I = 1/2 ( 1 Н и 13 С) этот угол прецессии равен 54 градуса 44’
Слайд 18
В классическом описании ядерные диполи прецессируют вокруг оси Z подобно волчку с произвольным значением угла. Частота прецессии (вращения) ядерного диполя (ларморова частота) пропорциональна плотности магнитного потока:
Слайд 20: Энергия ядер в магнитном поле
Магнитный диполь, помещенный в магнитное поле с плотностью потока B, обладает энергией, равной: Для ядра с ( 2I + 1) возможными ориентациями спина имеется ( 2I+ 1) дискретных энергетических состояний (ядерные Зеемановские уровни). Из выражений (5) и (7) получаем:
Слайд 21
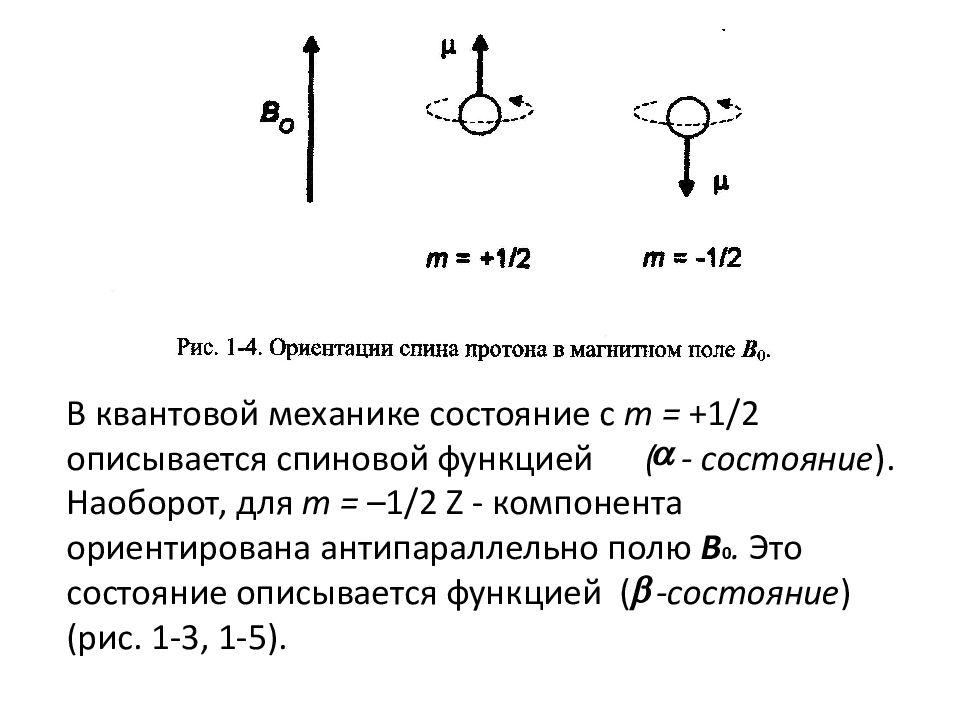
Для ядер со спином I = 1/2 ( 1 Н и 13 С) имеется два энергетических уровня в соответствии с двумя значениями магнитного квантового числа m. Если m = +1/2, то компонента магнитного момента ориентирована вдоль поля B и является энергетически более предпочтительной, т.е. характеризуется меньшей энергией.
Слайд 22
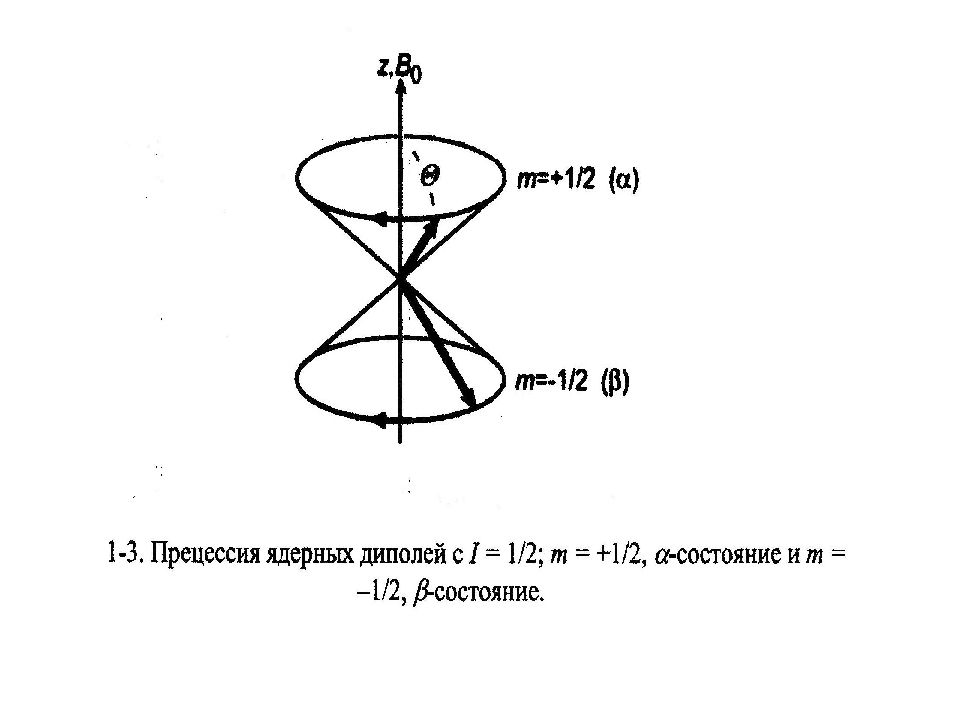
В квантовой механике состояние с m = +1/2 описывается спиновой функцией ( - состояние ). Наоборот, для m = –1/2 Z - компонента ориентирована антипараллельно полю B 0. Это состояние описывается функцией ( -состояние ) (рис. 1-3, 1-5).
Слайд 23
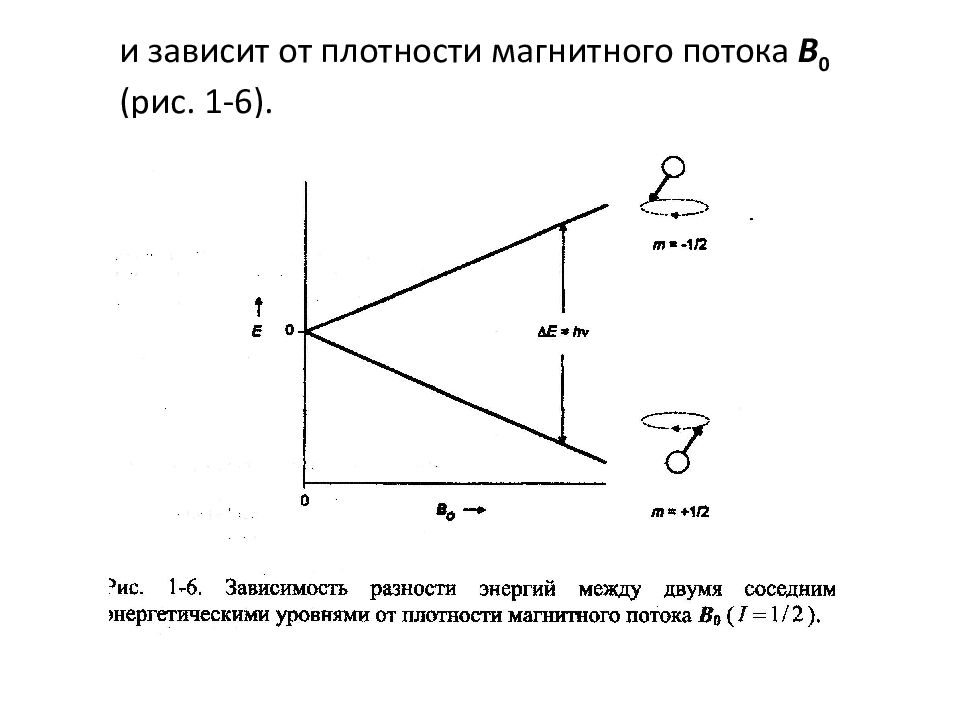
Различие в энергиях между двумя соседними энергетическими уровнями составляет:
Слайд 26: Основные принципы эксперимента ЯМР
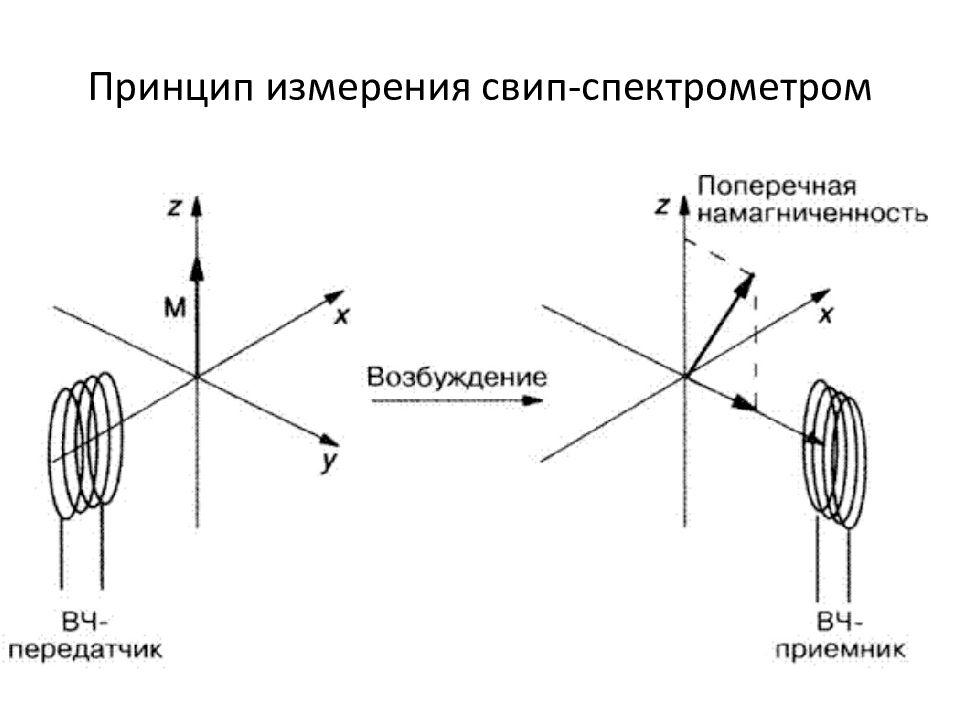
Условие резонанса реализуется тогда, когда для стимуляции переходов с разных энергетических уровней ядра облучают радиочастотным полем с соответствующей частотой ν 1. Переходы становятся возможны при выполнении следующего условия:
Слайд 27
Переходы ядер с нижнего уровня на верхний соответствуют поглощению энергии, а с верхнего уровня на нижний – испусканию энергии. Т.к. на нижнем уровне имеется некоторый избыток ядер, то преобладает процесс поглощения энергии облучающего радиочастотного поля. Интенсивность наблюдаемого сигнала поглощения пропорциональна разности населенностей уровней N α - N β, а следовательно, и полному числу спинов в образце (или концентрации ядер). Если же населенности равны, то сигнал не наблюдается, т.е. имеет место насыщение.
Слайд 28
Из выражений (6), (9) и (11) получаем условие резонанса: Термин “резонанс” относится к классической интерпретации явления ЯМР, поскольку переходы между энергетическими уровнями осуществляются только при совпадении частоты облучающего электромагнитного поля и частоты ларморовской прецессии вектора макроскопической ядерной намагниченности М.
Слайд 29
Но какие переходы разрешены, когда наблюдается более, чем два энергетических уровня, как в случае ядер со спином I ≥ 1 (рис. 1-4, правая часть), или для системы связанных ядер? Квантовая механика разрешает только те переходы, в которых магнитное квантовое число меняется на единицу: Таким образом, переходы могут иметь место только между соседними энергетическими уровнями (так, например, для изотопа 14 N переход с m = + 1 на m = - 1 запрещен).
Слайд 30
Экранирование и дезэкранирование магнитных ядер электронами в молекулах. Химический сдвиг. Во внешнем магнитном поле движущиеся электроны порождают локальные магнитные поля (правило Ленца), которые могут экранировать или дезэкранировать ядра σ - константа экранирования. В эфф = В 0 – В доп = (В 0 – В 0 ) = В 0 (1 - ) для протонов σ ≈ 10 -6 – 10 -7
Слайд 31
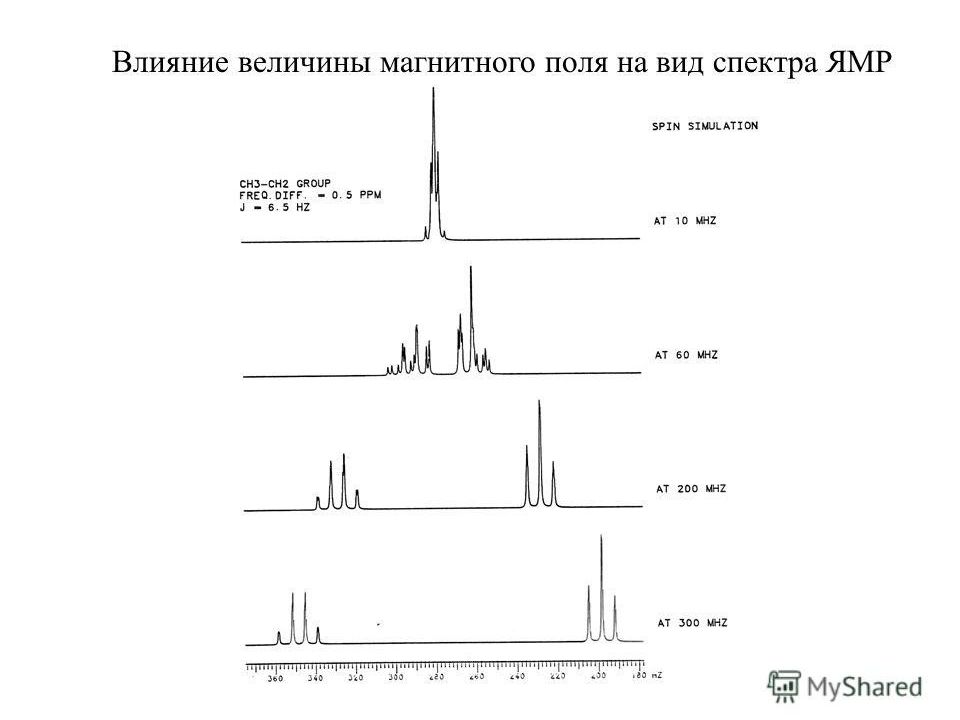
Величина σ определяется электронной плотностью около ядра и распределением электронной плотности в соседних структурных фрагментах. Поскольку значения электронной плотности в различных частях молекулы разные, ядра одного типа, находящиеся в химически неэквивалентных положениях в молекуле дают различные сигналы. Это явление называется химический сдвиг. С учетом экранирования В эф = В 0 (1 - σ), в спектрах одного и того же соединения, записанных на приборах с разными индукциями магнитных полей магнитов В 0, значения резонансных частот линий будут разными. Такие спектры трудно сравнивать.
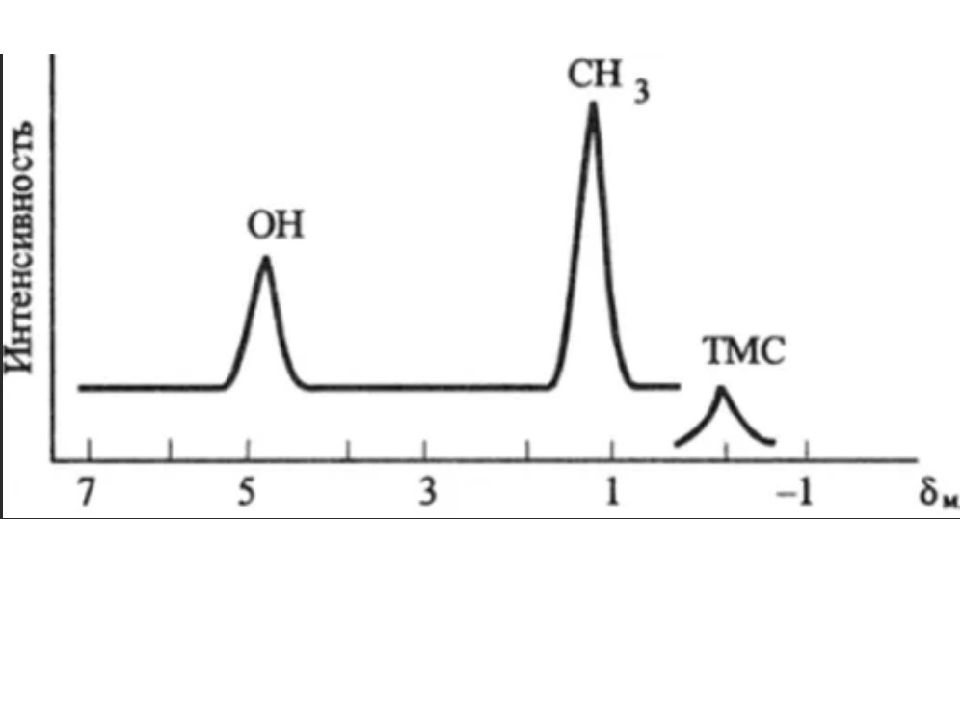
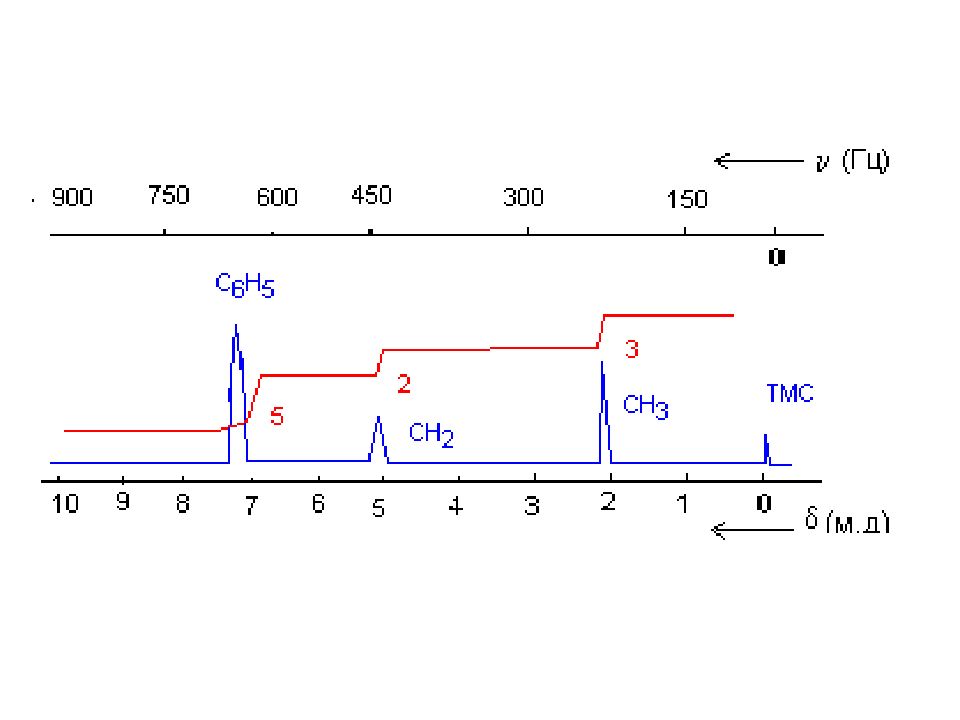
Слайд 32: Преодолеть эту трудность можно, если разделить значения резонансных частот на рабочую частоту прибора. Для удобства перед измерением спектра в образец добавляют небольшое количество эталонного соединения. Для спектров ЯМР- 1 Н и ЯМР- 13 С это тетраметилсилан (ТМС, Si (СН 3 ) 4 ). Соединение устойчиво, инертно химически, дает сильный и узкий сигнал (12 эквивалентных протонов ) на краю спектра, легко удаляется ( т.кип. 27 0 С )
Слайд 33
От каких факторов зависит положение сигнала (величина химического сдвига) протона? Для ответа на этот вопрос необходимо сделать некоторые уточнения. Дело в том, что магнитное поле, в котором находится данный протон, входящий в состав молекулы, редко бывает точно равно В 0. Вместо него на протон действует эффективное поле В эфф, несколько отличающееся от В 0. Приложенное поле В 0 заставляет электроны электронных оболочек циркулировать вокруг ядра, индуцируя тем самым магнитное поле, направленное против В 0. В результате ядро оказывается экранированным от полной напряженности приложенного магнитного поля.