Урок 9
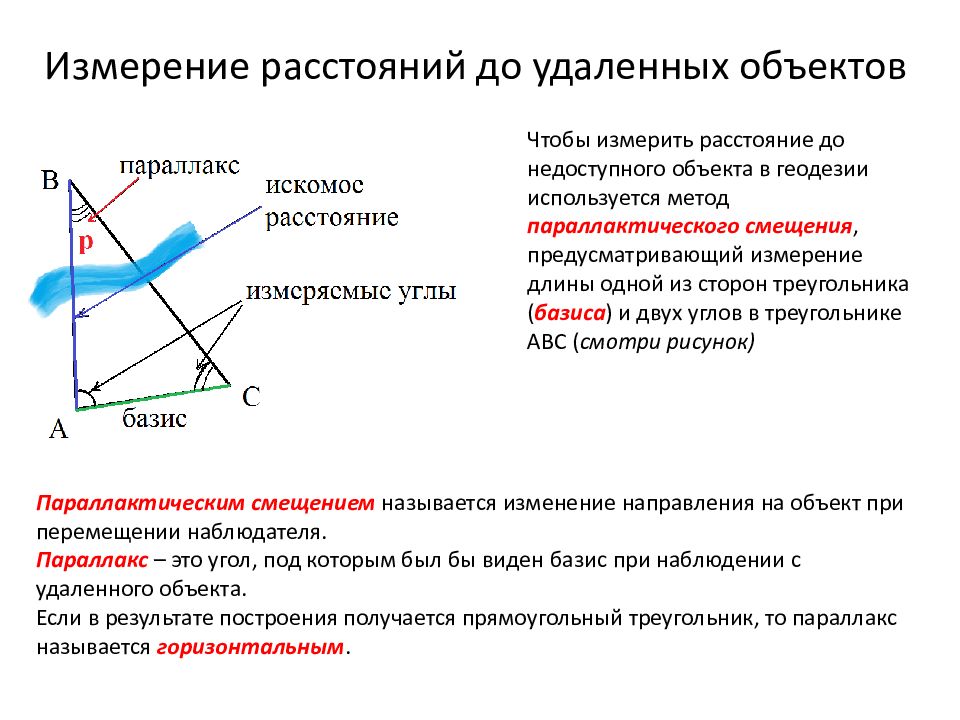
Чтобы измерить расстояние до недоступного объекта в геодезии используется метод параллактического смещения, предусматривающий измерение длины одной из сторон треугольника ( базиса ) и двух углов в треугольнике АВС ( смотри рисунок) Параллактическим смещением называется изменение направления на объект при перемещении наблюдателя. Параллакс – это угол, под которым был бы виден базис при наблюдении с удаленного объекта. Если в результате построения получается прямоугольный треугольник, то параллакс называется горизонтальным.
Если объект очень удален, то, чтобы можно было измерить его параллакс, базис должен быть очень большим. Для определения расстояния от Земли до объектов Солнечной системы (будем называть их светилами) в качестве базиса используют экваториальный радиус Земли. Горизонтальный параллакс светила – это угол, под которым со светила был бы виден экваториальный радиус Земли, перпендикулярный лучу зрения.
Из математики : для малых углов Параллакс в астрономии измеряют в секундах. Найдем, сколько секунд в 1 радиане: ’’ С большой долей точности можно считать, что
Формула для вычисления расстояния D до светила при известном радиусе Земли и измеренном горизонтальном параллаксе (в угловых секундах) : Измерив горизонтальные параллаксы объектов Солнечной системы, ученые-астрономы смогли определить расстояния до планет, Солнца и Луны.
Найти расстояние от Земли до Луны, если горизонтальный параллакс Луны 57 ’. Радиус Земли 6371 км. Дано : p=57’ R=6 371 км Решение : 57’=57∙60’’=3420’’ 384244 км Найти : D Ответ : расстояние от Земли до Луны примерно 384000 км. Дано : p=57’ R=6 371 км Найти : D Ответ : расстояние от Земли до Луны примерно 384000 км.
На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0.9 ’’ ? Параллакс Солнца 8.8 ’’. Дано : p C =8.8’’ p 1 =0.9’’ D С =1 а.е. Решение : Найти : Ответ : расстояние от Земли до Сатурна 9.8 астрономических единицы. Дано : p C =8.8’’ p 1 =0.9’’ D С =1 а.е. Ответ : расстояние от Земли до Сатурна 9.8 астрономических единицы.
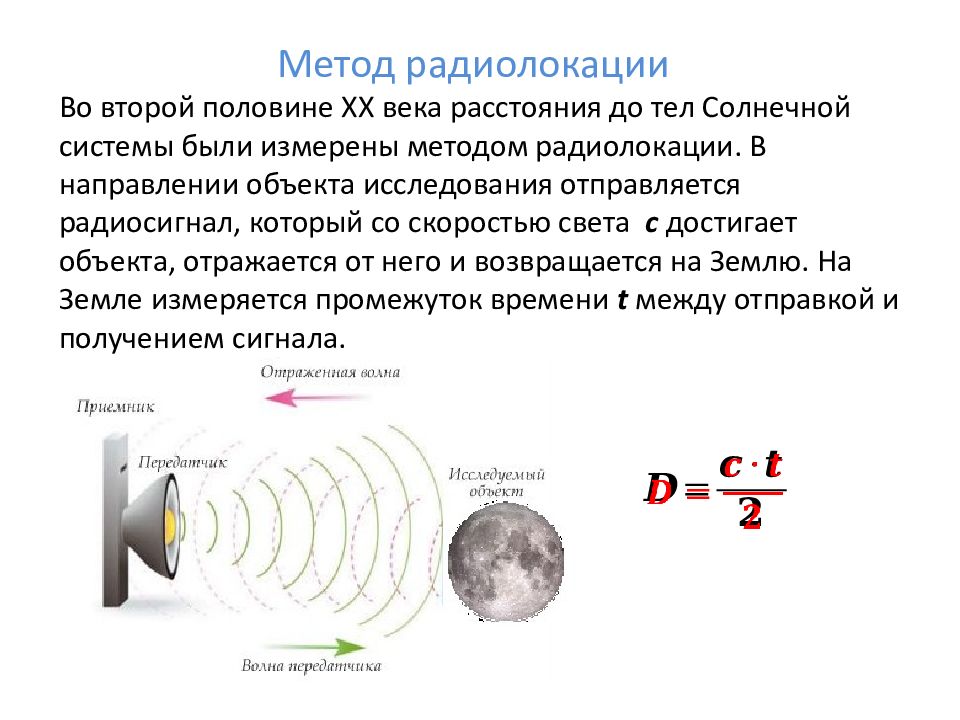
Во второй половине ХХ века расстояния до тел Солнечной системы были измерены методом радиолокации. В направлении объекта исследования отправляется радиосигнал, который со скоростью света c достигает объекта, отражается от него и возвращается на Землю. На Земле измеряется промежуток времени t между отправкой и получением сигнала.
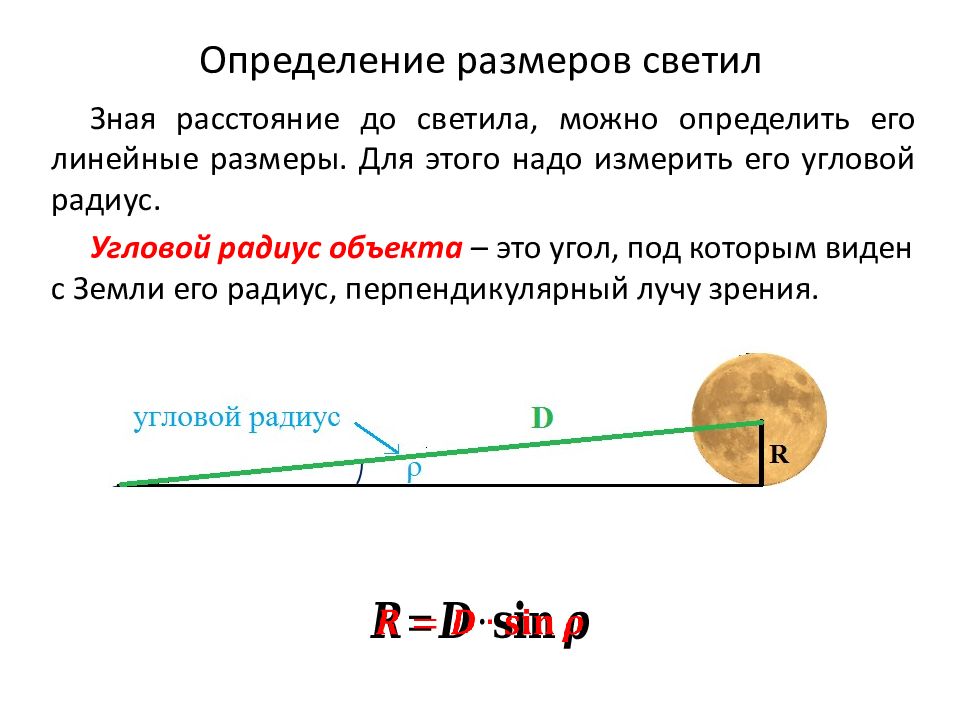
Зная расстояние до светила, можно определить его линейные размеры. Для этого надо измерить его угловой радиус. Угловой радиус объекта – это угол, под которым виден с Земли его радиус, перпендикулярный лучу зрения.
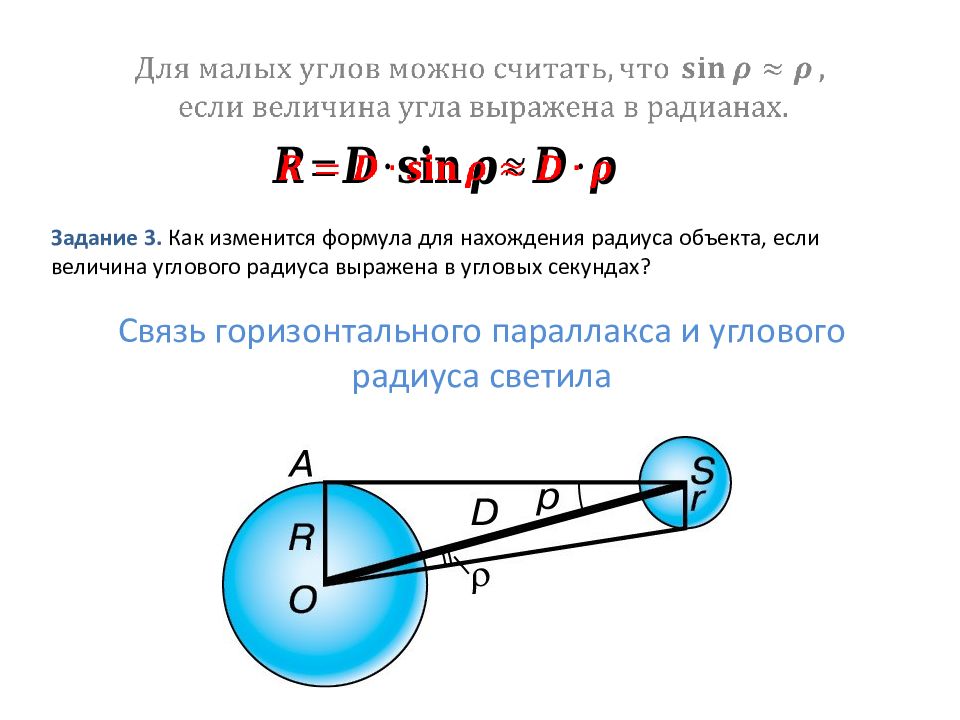
Задание 3. Как изменится формула для нахождения радиуса объекта, если величина углового радиуса выражена в угловых секундах? Связь горизонтального параллакса и углового радиуса светила
4. Во сколько раз диаметр Солнца больше диаметра Луны, если их угловые диаметры одинаковы, а горизонтальные параллаксы равны 8.8 ’’ и 57 ’ соответственно? 5. Чему равен угловой диаметр Солнца при наблюдении с Нептуна, расстояние до которого 30 а.е., если угловой диаметр Солнца при наблюдении с Земли – 0.5 0 ? 6. Радиолокатор зафиксировал отраженный сигнал от пролетающего вблизи Земли астероида через t = 0,667 с. На каком расстоянии от Земли находился в это время астероид? Задания для закрепления
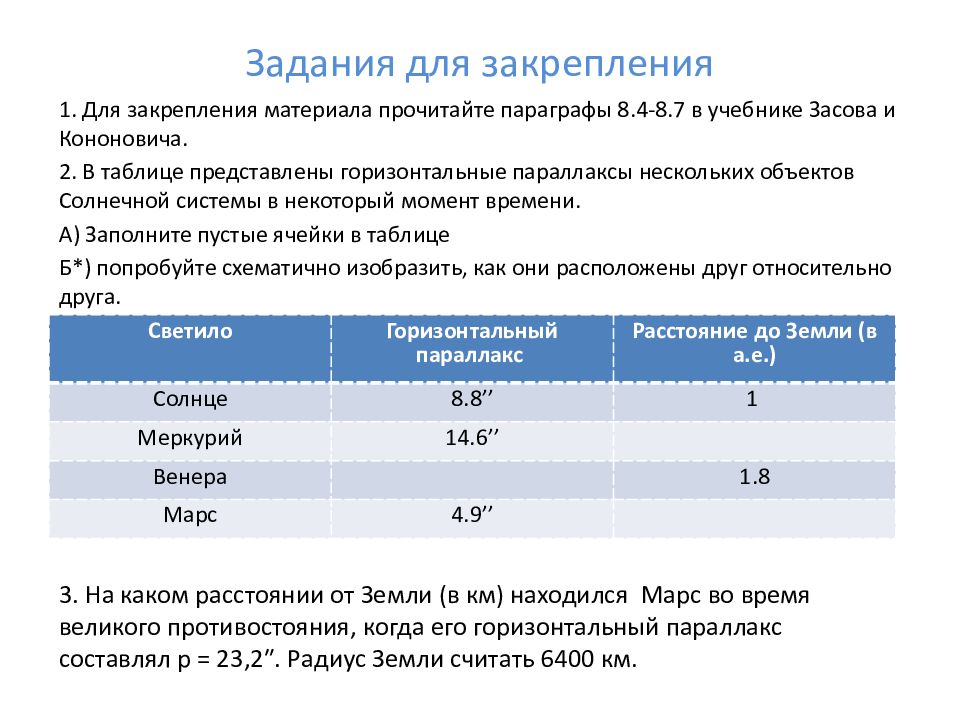
1. Для закрепления материала прочитайте параграфы 8.4-8.7 в учебнике Засова и Кононовича. 2. В таблице представлены горизонтальные параллаксы нескольких объектов Солнечной системы в некоторый момент времени. А) Заполните пустые ячейки в таблице Б*) попробуйте схематично изобразить, как они расположены друг относительно друга. Светило Горизонтальный параллакс Расстояние до Земли (в а.е.) Солнце 8.8 ’’ 1 Меркурий 14.6’’ Венера 1.8 Марс 4.9’’ 3. На каком расстоянии от Земли ( в км ) находился Марс во время великого противостояния, когда его горизонтальный параллакс составлял p = 23,2″. Радиус Земли считать 6400 км.
