Первый слайд презентации: Преобразования графиков функций
Слайд 2: Оглавление
Правила преобразований графиков функций Графические иллюстрации Примеры построения графиков сложных функций с помощью одного преобразования Примеры построения графиков сложных функций с помощью нескольких преобразований
Слайд 3: Правила преобразований графиков функций
Построение графика функции y=f(x+a) Построение графика функции y=f(x)+b Построение графика функции y=f(-x) Построение графика функции y=-f(x) Построение графика функции y=f(kx) Построение графика функции y=kf(x) Построение графика функции y=f(|x|) Построение графика функции y=|f(x)| оглавление Правила преобразований графиков функций
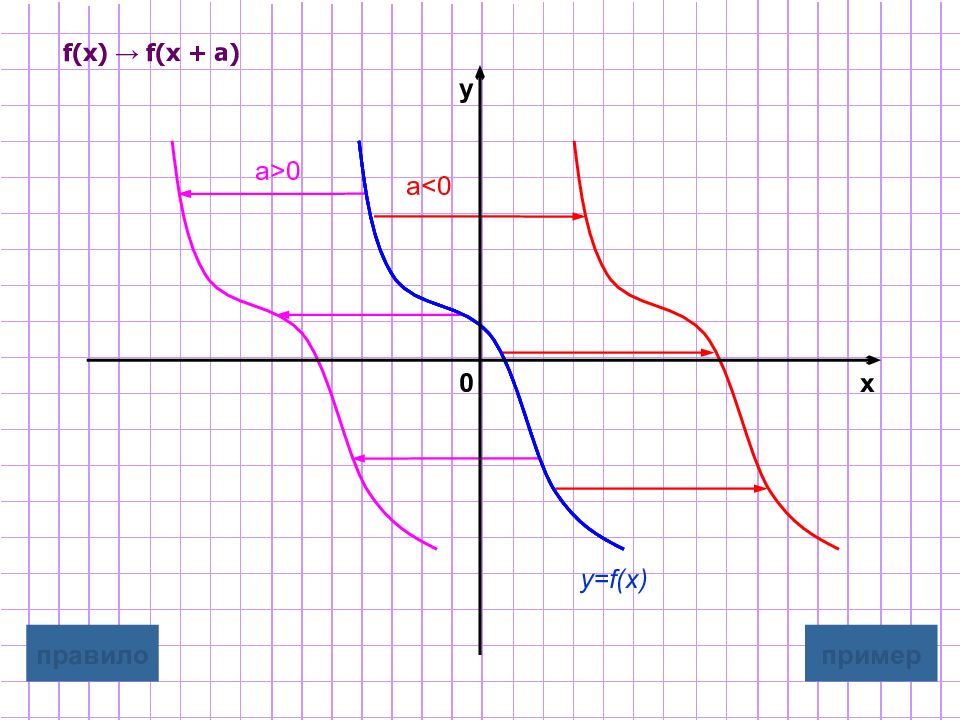
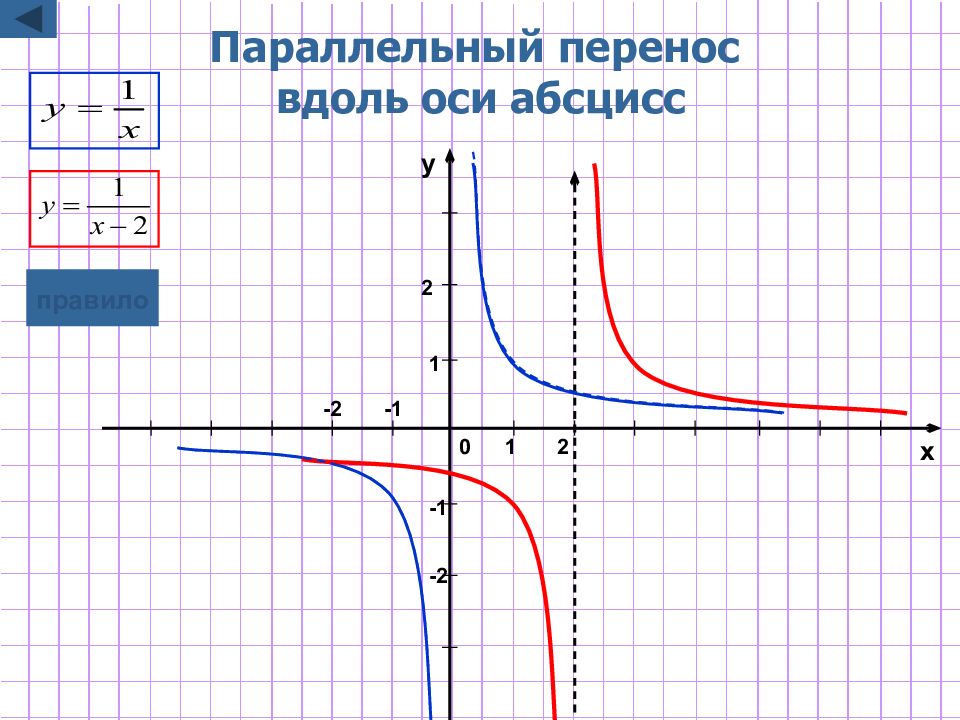
Слайд 4: Параллельный перенос вдоль оси абсцисс
y=f(x + a) Для построения графика функции y=f(x+a) надо график функции y=f(x) параллельно перенести на |a| единиц вдоль оси Ox в положительном направлении, если a<0 в отрицательном направлении, если a>0 графическая иллюстрация
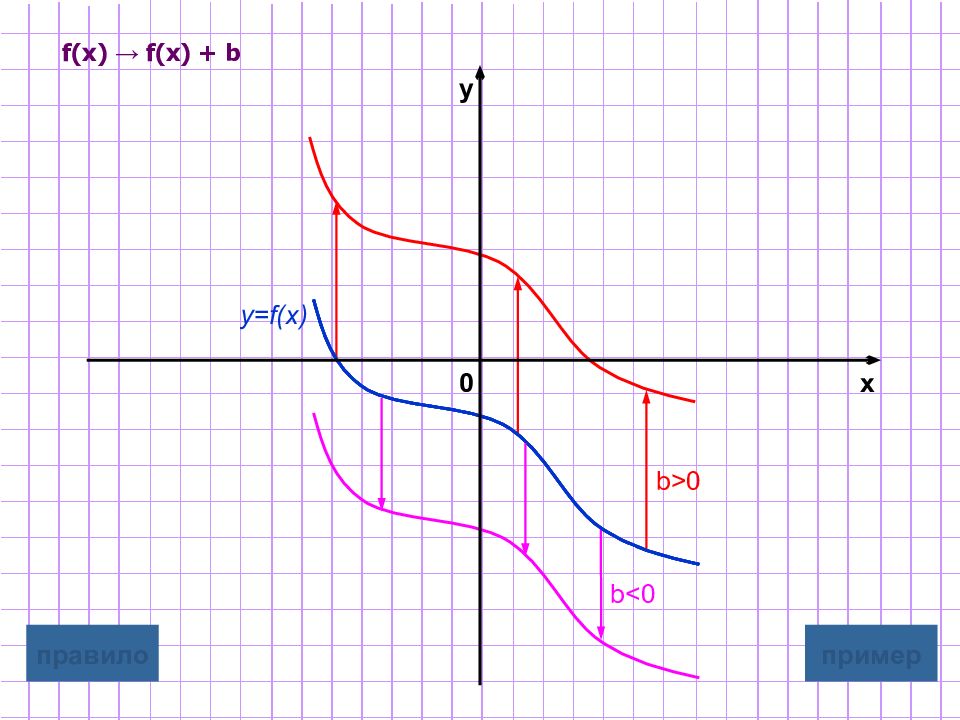
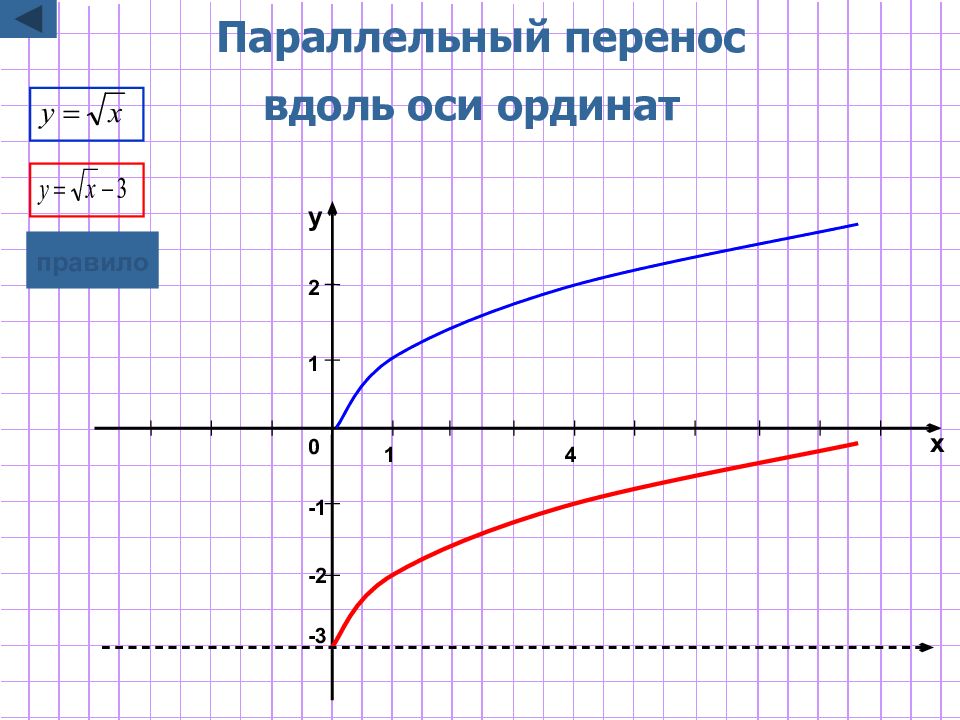
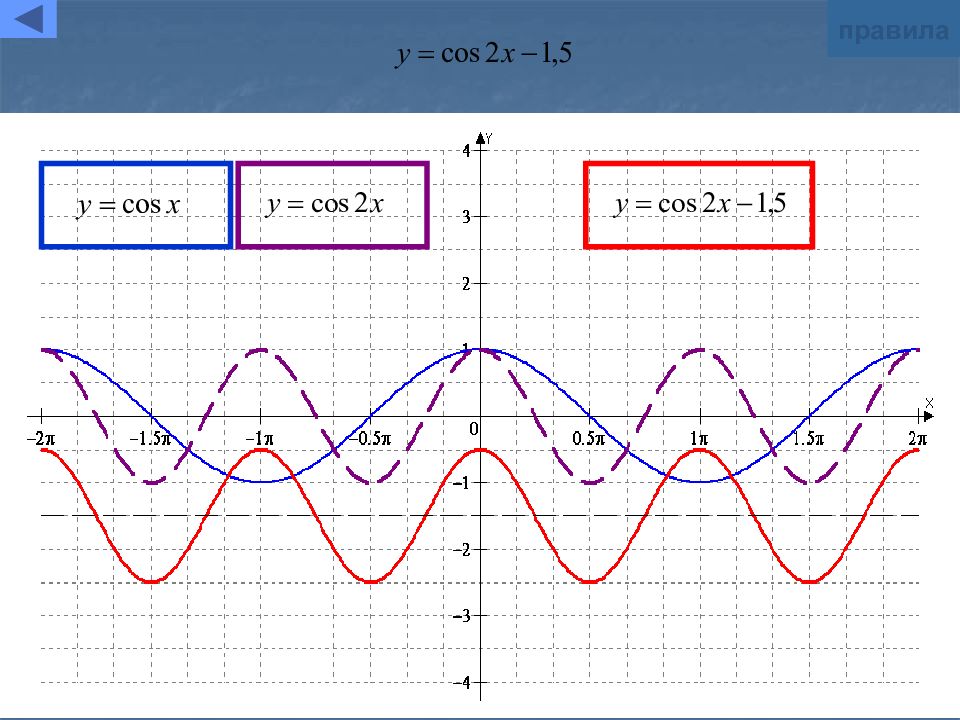
Слайд 5: Параллельный перенос вдоль оси ординат
y=f(x)+b Для построения графика функции y=f(x)+b надо график функции y=f(x) параллельно перенести на |b| единиц вдоль оси Oy в положительном направлении, если b>0 в отрицательном направлении, если b<0 графическая иллюстрация
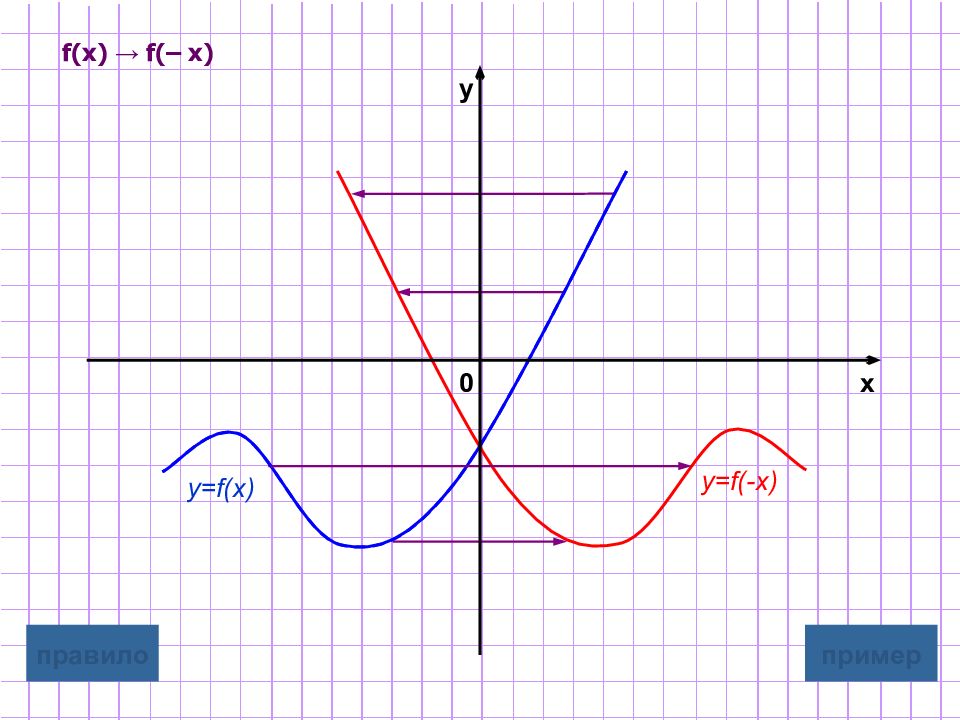
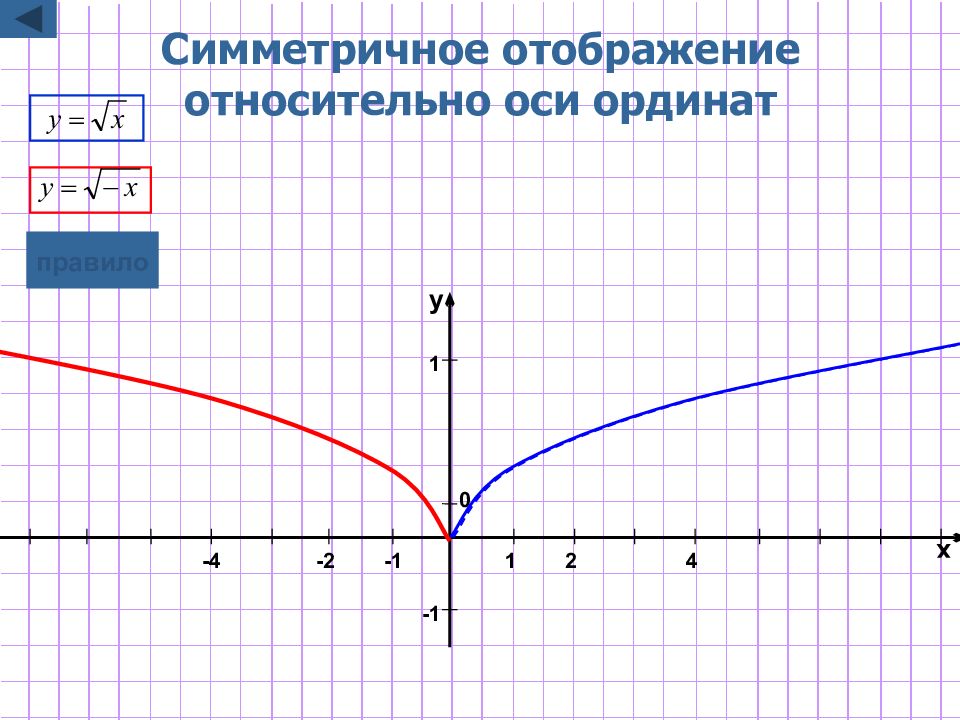
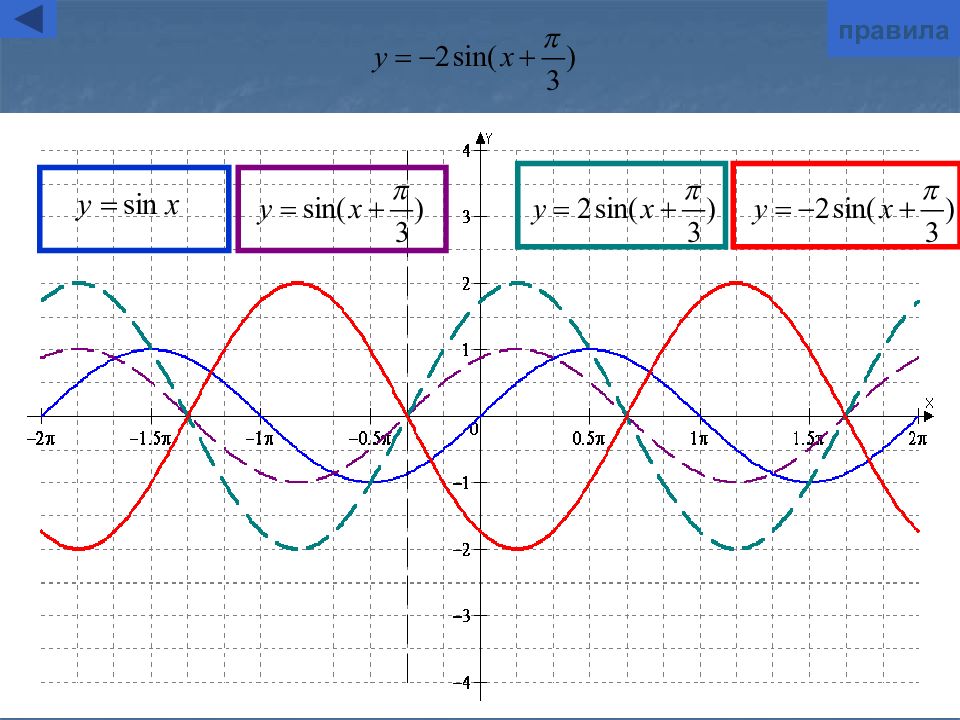
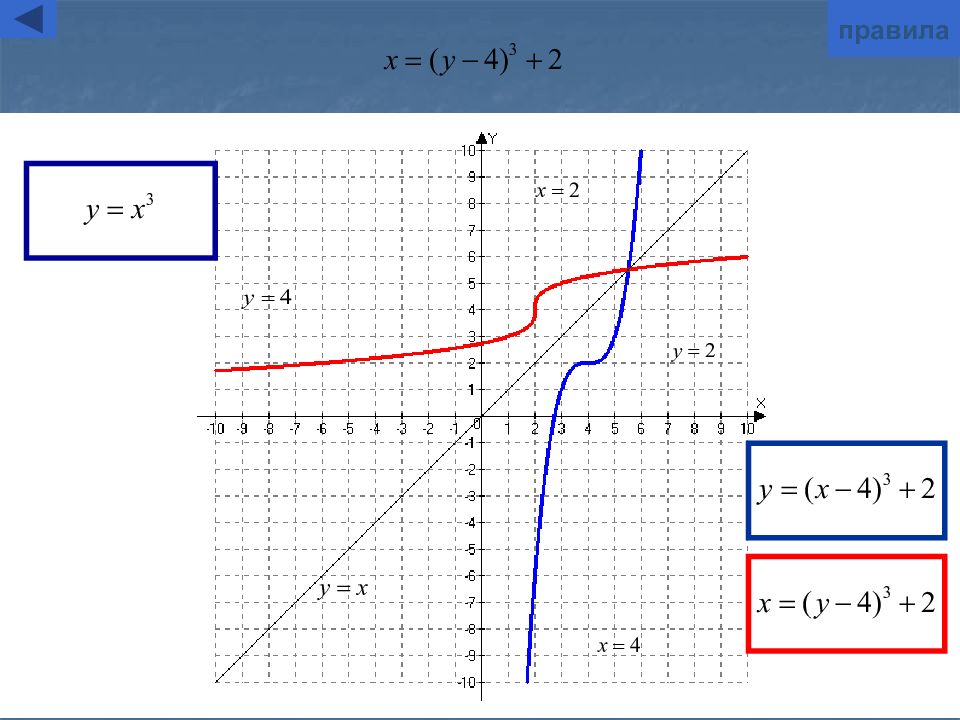
Слайд 6: Симметричное отображение относительно оси ординат
y=f( - x) Для построения графика функции y=f( - x) надо график функции y=f(x) симметрично отобразить относительно оси Oy Замечание : при этом точки пересечения с осью у остаются неизменными. графическая иллюстрация
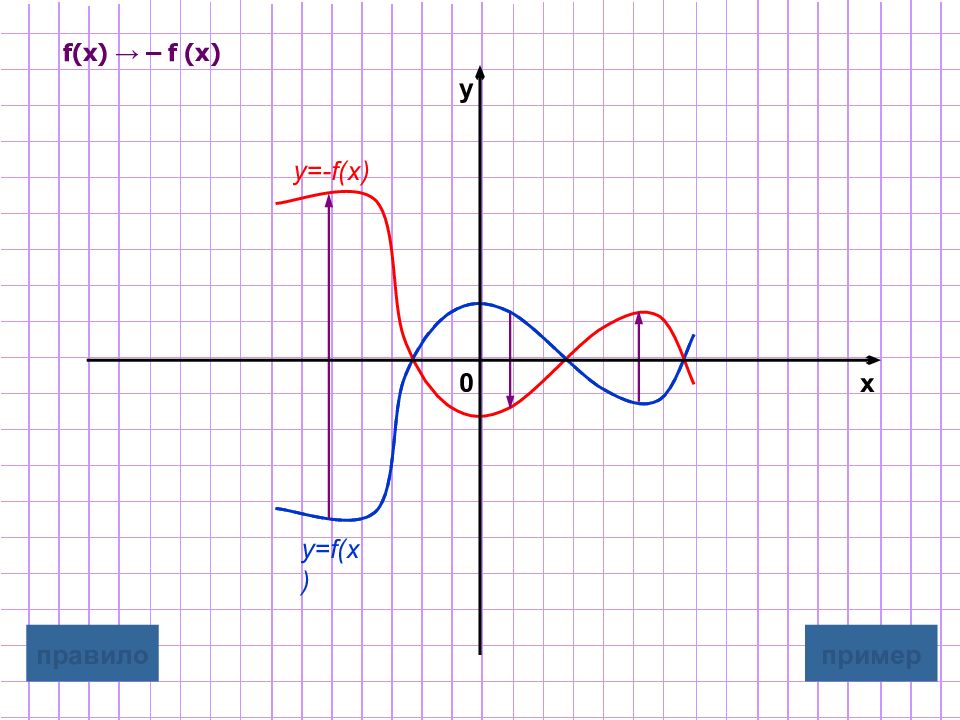
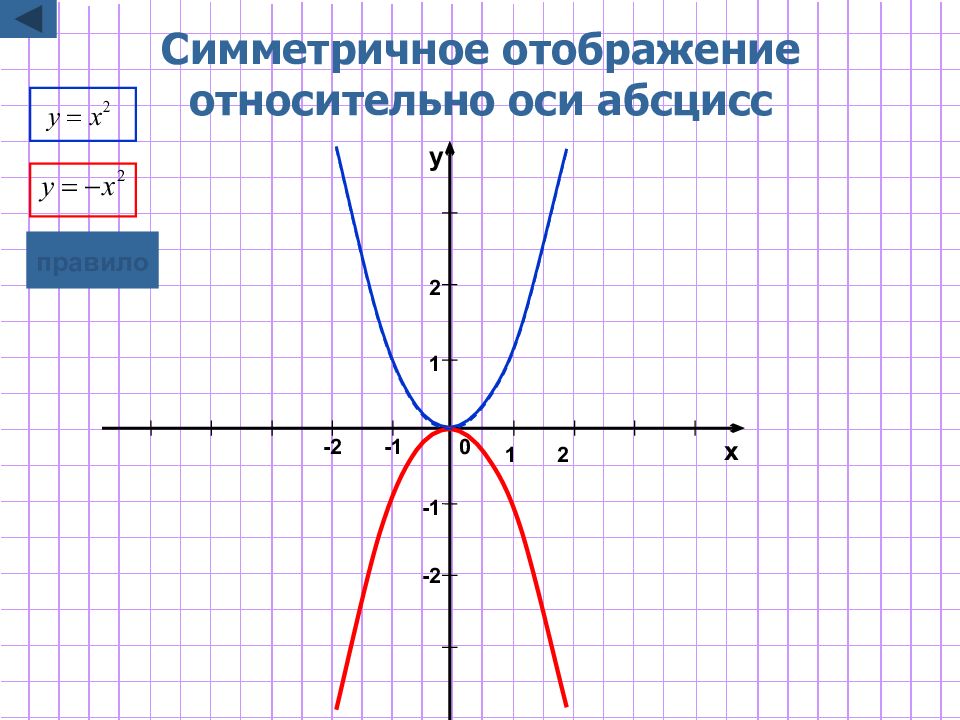
Слайд 7: Симметричное отображение относительно оси абсцисс
y= - f(x) Для построения графика функции y= - f(x) надо график функции y=f(x) симметрично отобразить относительно оси Ox Замечание : при этом точки пересечения с осью х остаются неизменными. графическая иллюстрация
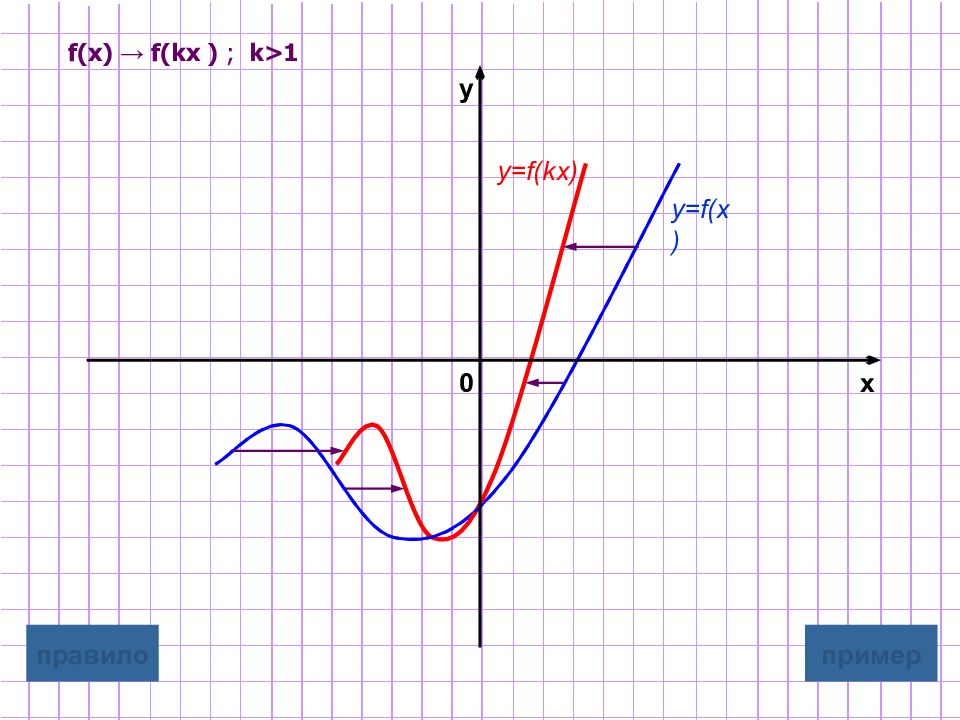
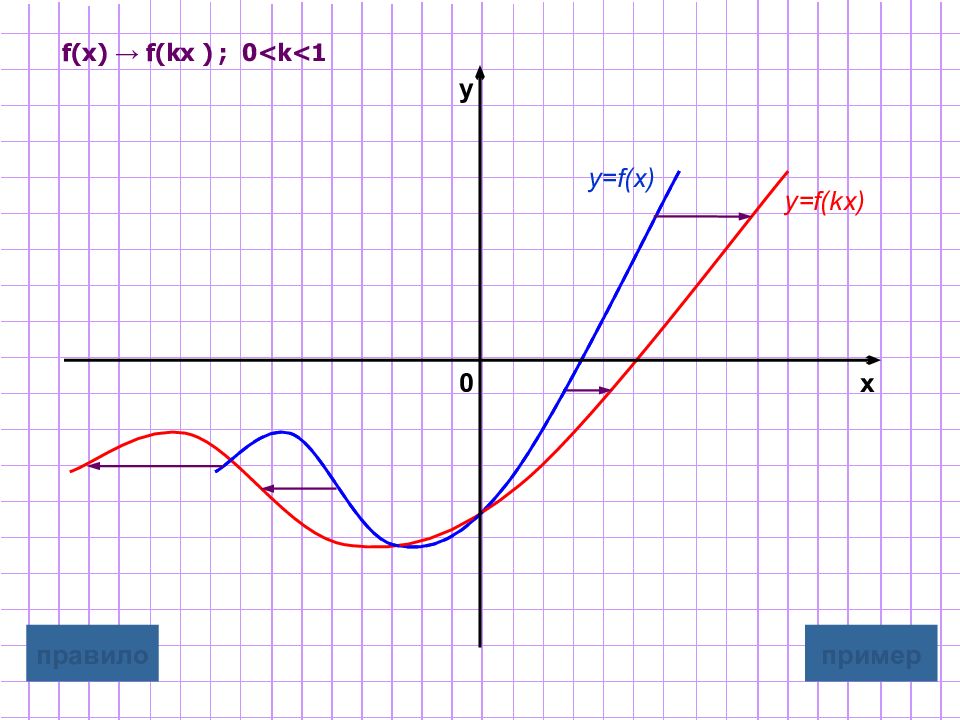
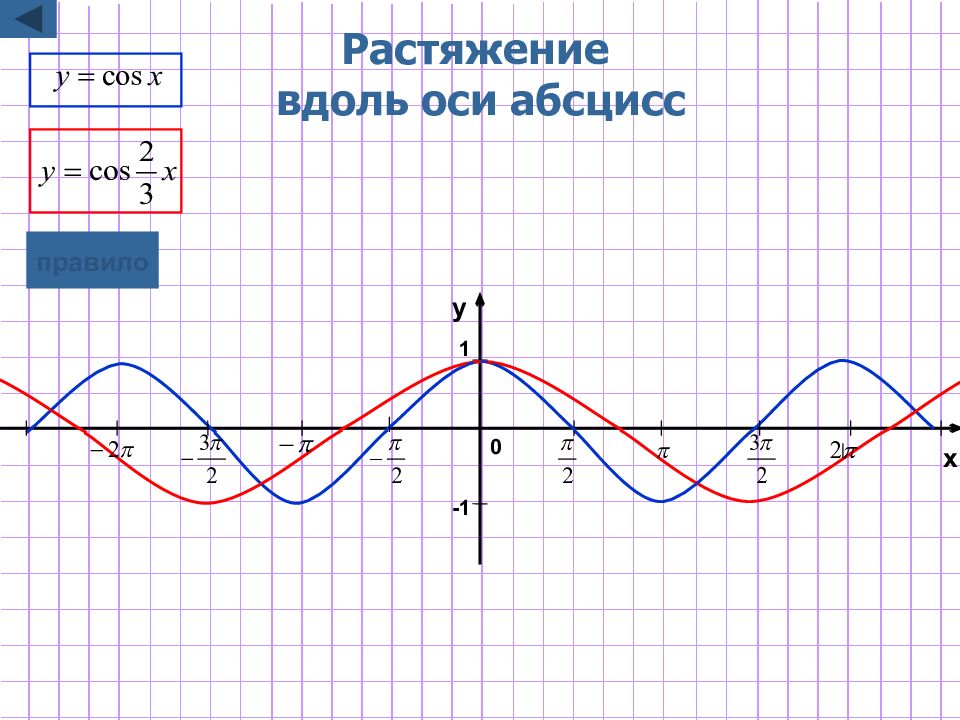
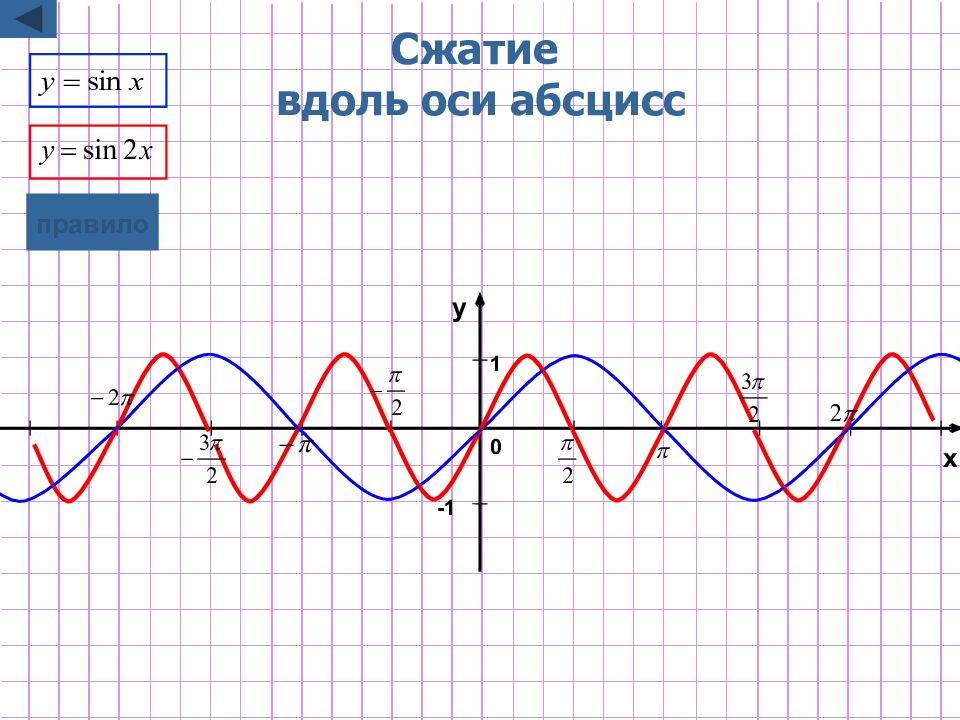
Слайд 8: Растяжение / сжатие вдоль оси абсцисс
y=f(kx) Для построения графика функции y=f(kx) надо график функции y=f(x) подвергнуть масштабированию вдоль оси Ox растяжению в 1 /k раз, если 0 <k<1 сжатию в k раз, если k>1 Замечание : при этом точки пересечения с осью у остаются неизменными. графическая иллюстрация 1 графическая иллюстрация 2
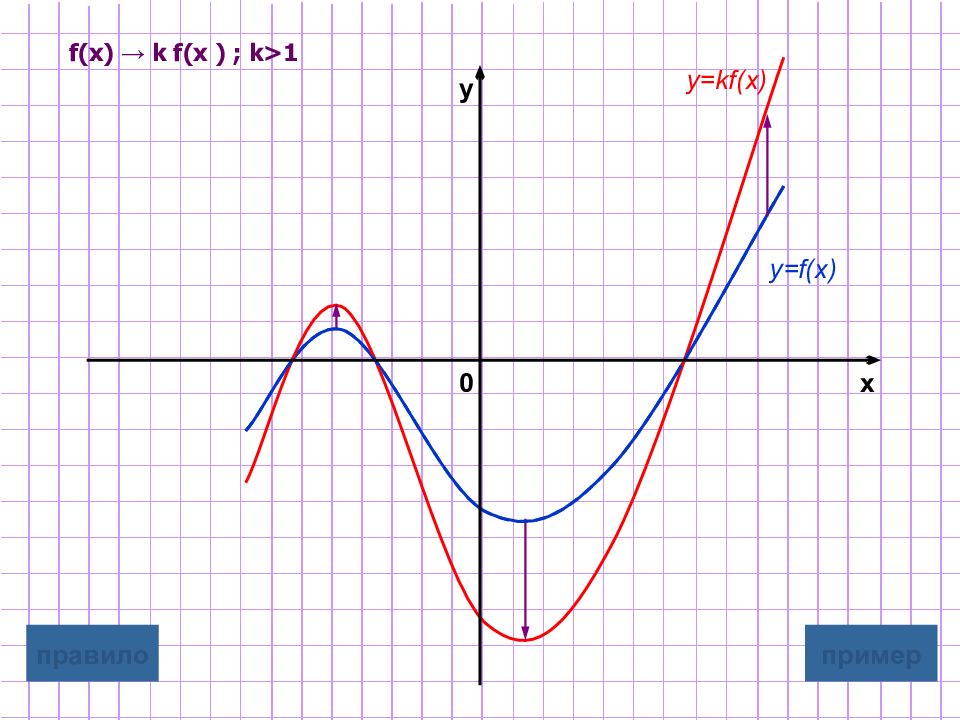
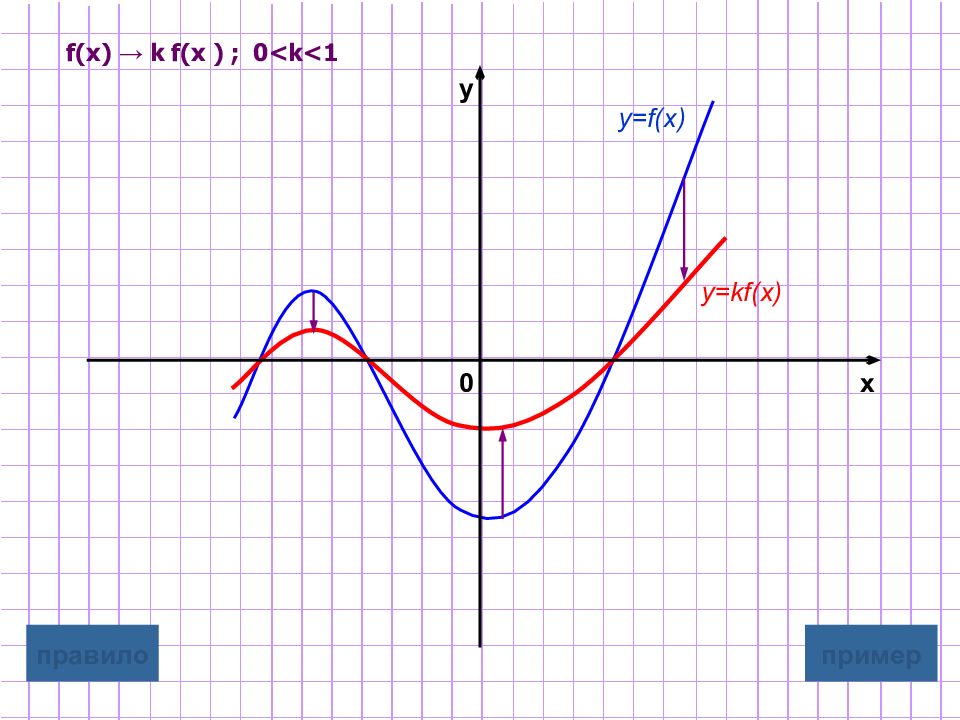
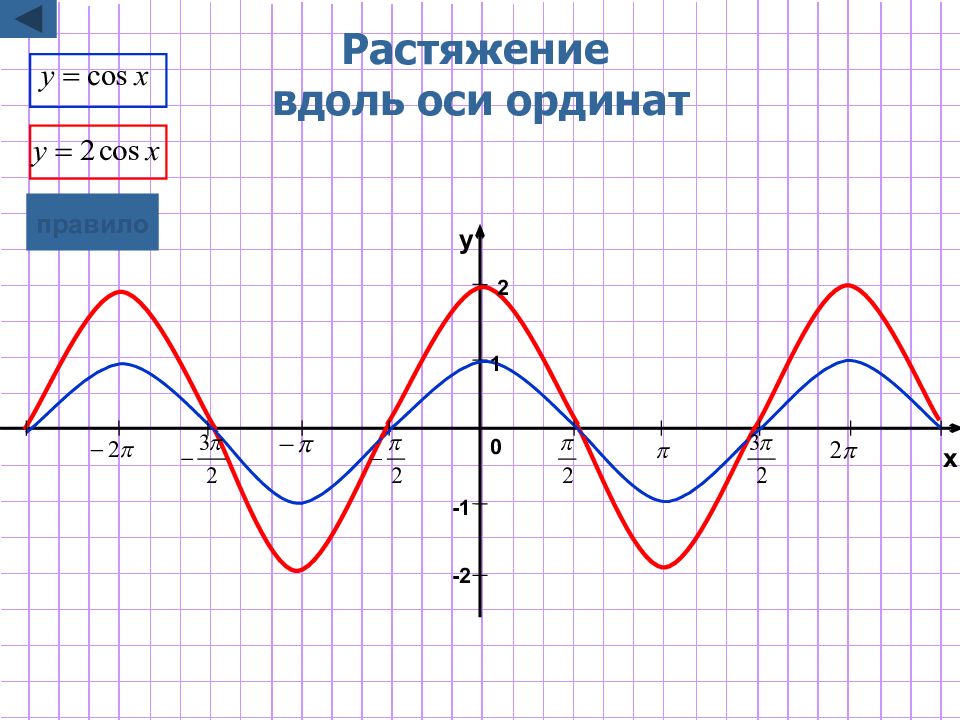
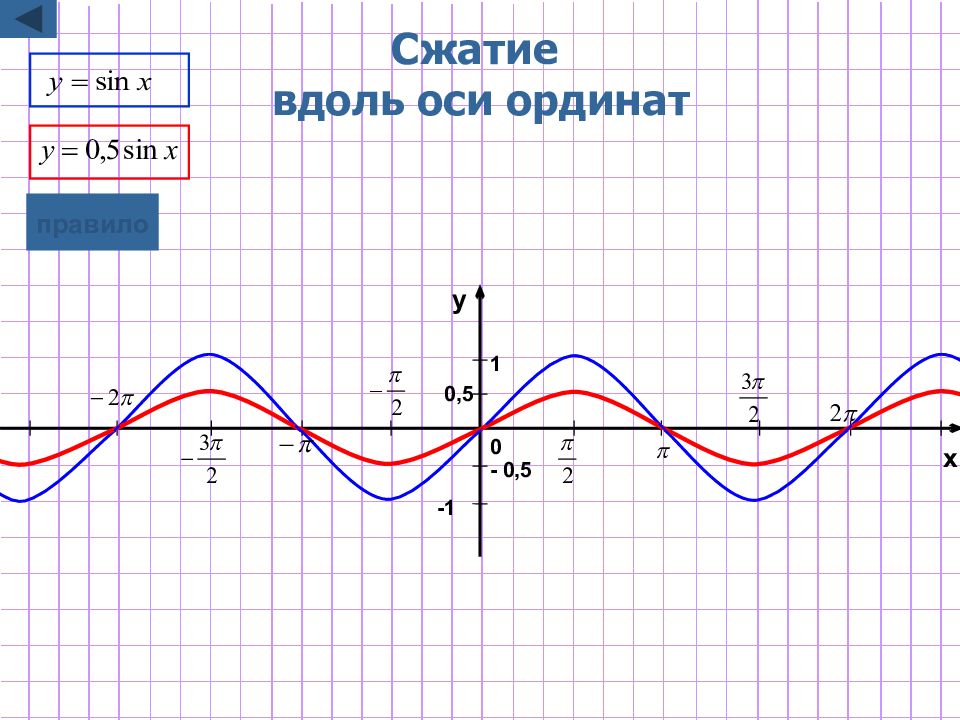
Слайд 9: Растяжение / сжатие вдоль оси ординат
y=kf(x) Для построения графика функции y=kf(x) надо график функции y=f(x) подвергнуть масштабированию вдоль оси Oy растяжению в k раз, если k>1 сжатию в 1 /k раз, если 0 <k<1 Замечание : при этом точки пересечения с осью х остаются неизменными. графическая иллюстрация 2 графическая иллюстрация 1
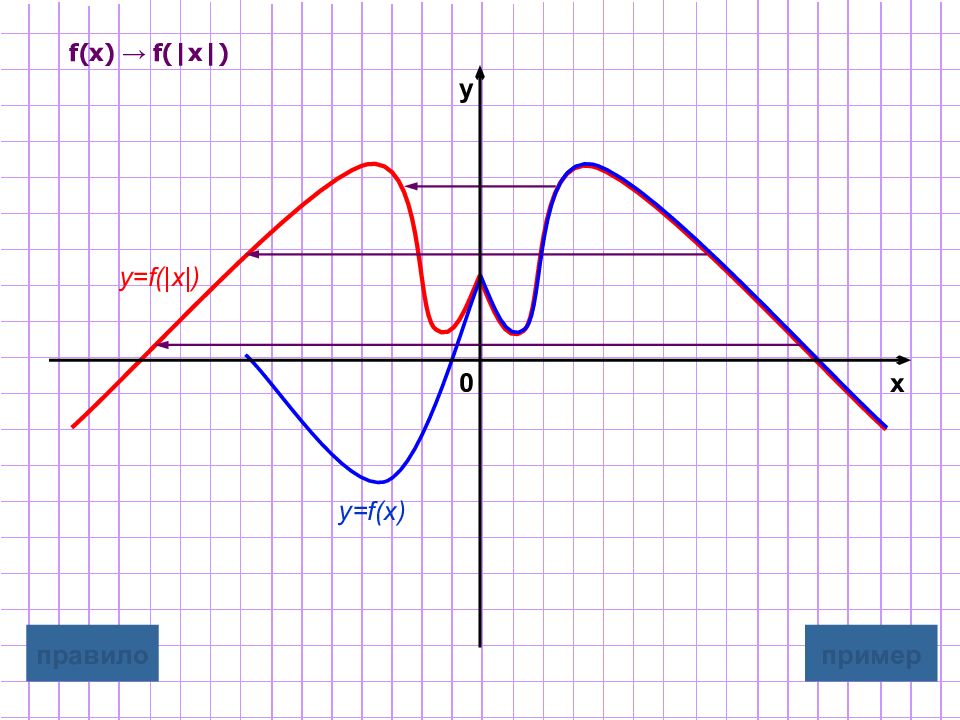
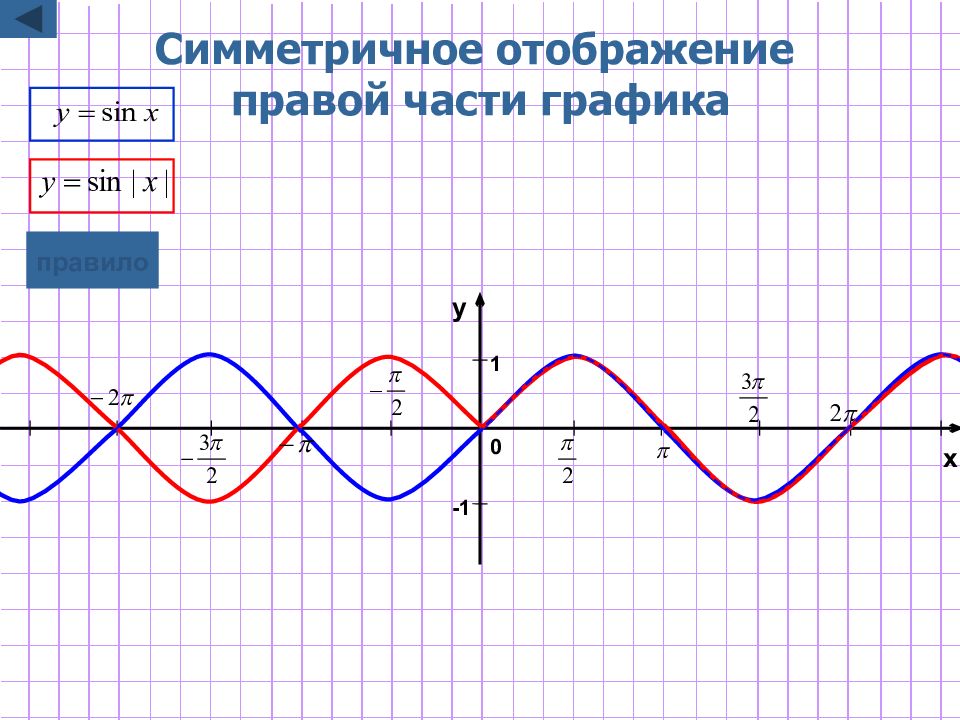
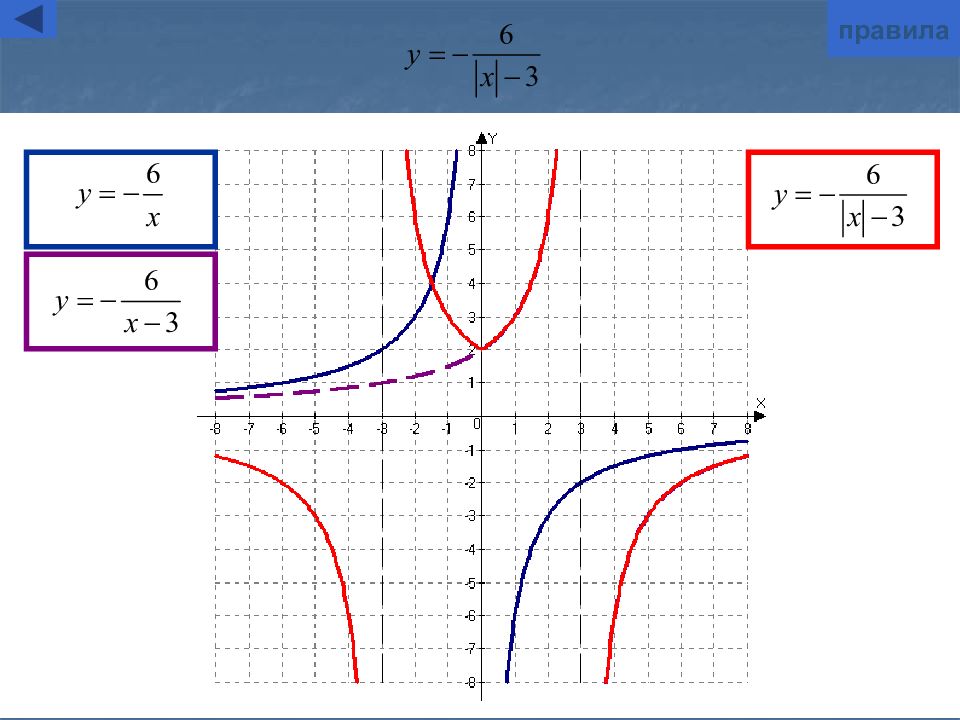
Слайд 10: Построение графика y=f(|x|)
y=f(|x|) Для построения графика функции y=f(|x|) надо : часть графика функции y=f(x), лежащую правее оси Oy, оставить без изменения ; эту же часть графика функции y=f(x), лежащую правее оси Oy, симметрично отобразить относительно оси О y графическая иллюстрация
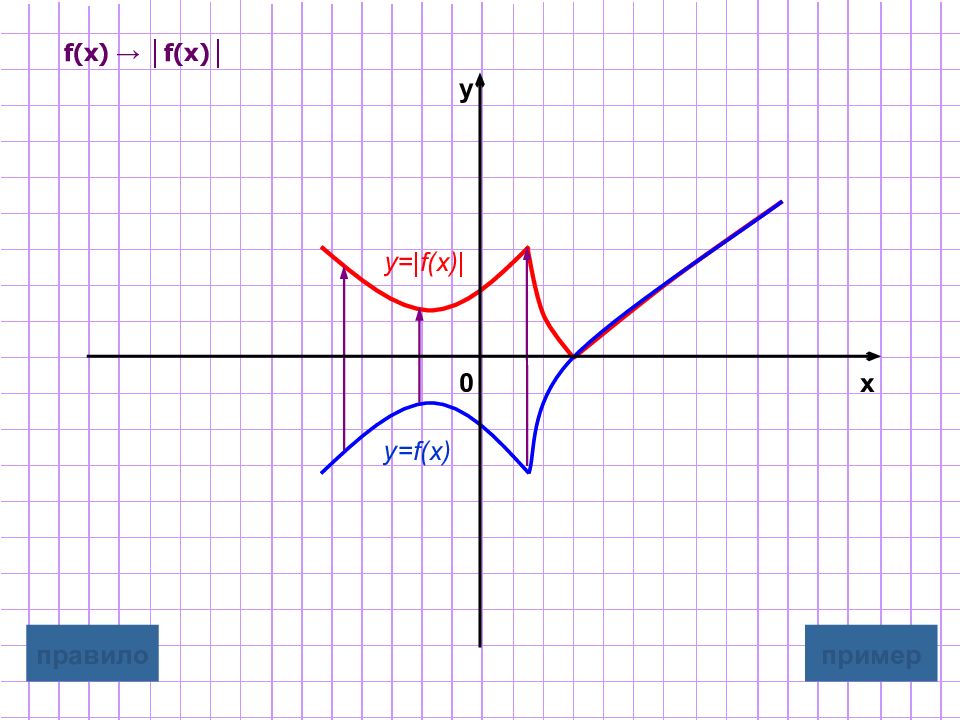
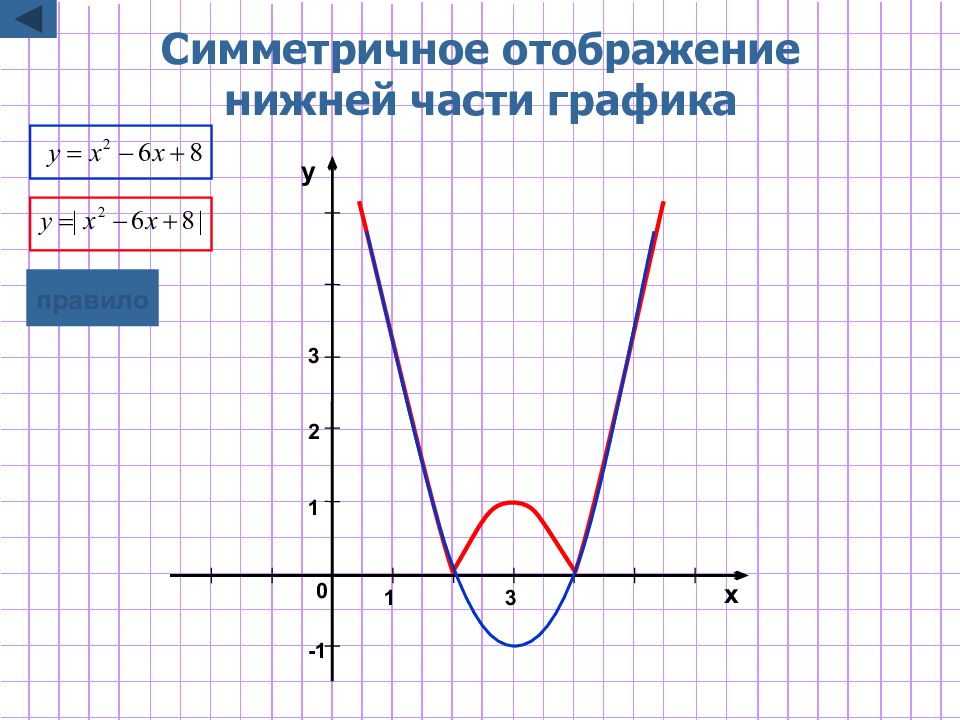
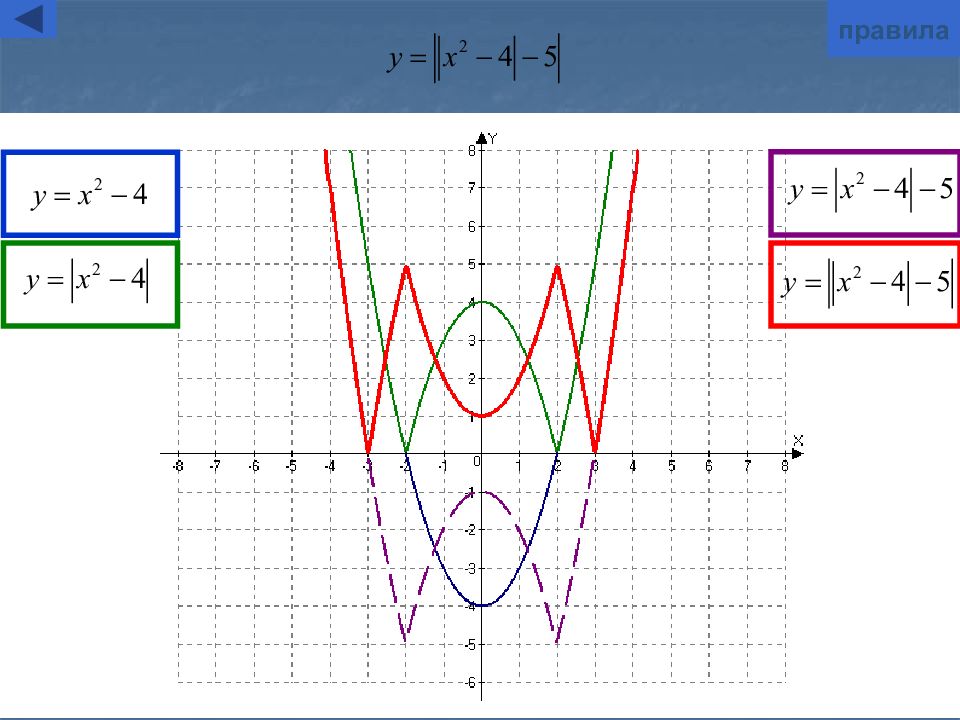
Слайд 11: Построение графика y=|f(x)|
y=|f(x)| Для построения графика функции y=|f(x)| надо : часть графика функции y=f(x), лежащую выше оси O х, оставить без изменения ; часть графика функции y=f(x), лежащую ниже оси O х, симметрично отобразить относительно оси Ох графическая иллюстрация
Слайд 12: Графические иллюстрации
Построение графика функции y=f(x+a) Построение графика функции y=f(x)+b Построение графика функции y=f(-x) Построение графика функции y=-f(x) Построение графика функции y=f(kx), 0<k<1 Построение графика функции y=f(kx), k>1 Построение графика функции y=kf(x), 0<k<1 Построение графика функции y=kf(x), k>1 Построение графика функции y=f(|x|) Построение графика функции y=|f(x)| оглавление примеры правила
Слайд 23: Примеры построения графиков сложных функций
Построение графика функции y=f(x+a) Построение графика функции y=f(x)+b Построение графика функции y=f(-x) Построение графика функции y=-f(x) Построение графика функции y=f(kx), 0<k<1 Построение графика функции y=f(kx), k>1 Построение графика функции y=kf(x), 0<k<1 Построение графика функции y=kf(x), k>1 Построение графика функции y=f(|x|) Построение графика функции y=|f(x)| оглавление
Слайд 24: Параллельный перенос вдоль оси абсцисс
-2 -1 1 2 x y 1 2 0 Параллельный перенос вдоль оси абсцисс -1 -2 правило
Слайд 25: Параллельный перенос вдоль оси ординат
-2 -1 1 2 x y 1 4 0 -3 Параллельный перенос вдоль оси ординат правило
Слайд 26: Симметричное отображение относительно оси абсцисс
-2 -1 1 2 x y 1 2 0 Симметричное отображение относительно оси абсцисс -1 -2 правило
Слайд 27: Симметричное отображение относительно оси ординат
-1 1 x y 1 2 0 Симметричное отображение относительно оси ординат -1 -2 4 -4 правило
Слайд 32: Симметричное отображение нижней части графика
-1 1 2 x y 1 0 3 3 Симметричное отображение нижней части графика правило